高空悬缆振动的主动控制研究
2020-04-28陈贵亮张守林郭士杰
陈贵亮,张守林,杨 冬,郭士杰
(河北工业大学机械工程学院,天津 300130;河北省智能传感与人机融合重点实验室,天津 300130)
1 引言
悬缆具有纵向刚度、强度大和重量轻等优点被广泛应用于斜拉索桥梁、载人电梯、起重机、建筑外墙施工等工程,但也因横向振动差,易振动且不易控制等缺点而制约了其应用效果。因而长悬缆在诸多类似机构中存在的振动问题的控制研究对其应用品质的提高意义重大。文献[1]提出了一种非线性动力学模型对桥梁振动做了分析,并对缆索参数激励横向振动做了研究;文献[2]建立了提升钢丝绳的数学模型,在不同的工况下,研究了钢丝绳的振动特性;文献[3-4]对矿井钢丝绳的振动做了研究,采用的是能量法和hamilton原理,对钢丝绳的振动进行了简化,在外加周期性激励的作用下,建立了提升钢丝绳纵向振动的动力学方程,并对其特性进行了详细的分析。在这些研究中,通过应用多种方法建立悬缆的振动模型[5],进而对其振动特性进行了分析,对认识悬缆振动的规律很有意义。文献[6]对提升钢丝绳进行仿真模型建立,通过simulink仿真,在各种因素影响下,提出改善和抑制钢丝绳振动的抑制方法;文献[7]对多维振动下结构的振动进行了主动控制研究,并提出自适应模糊神经网络控制的方法,经验证控制效果良好;文献[8]提出了一种自适应神经网络模糊推理系统,该系统利用大量的数据样本进行学习,对特性非常复杂的系统有实用价值;文献[9]提出了一种将神经网络和模糊控制的规则相结合的控制方法,经验证该方法对于减振而言是合理的。由上可看出,对于悬缆机构的振动研究主要为:(1)振动模型的建立和分析;(2)抑振方法的研究。该文以河北某大学研究的高层建筑幕墙安装机器人高空平台为背景,对平台采用的悬缆进行振动研究,具体思路是:首先建立长悬缆的振动动力学模型,利用BP网络对模糊控制规则进行记忆,设计模糊神经网络抑振系统,针对一定的振动频带施加相位相反的外加主动激励,使之与高空悬缆的原有振动能量抵消,对高空悬缆的振动进行仿真研究,并进一步通过试验验证仿真结果和抑振效果。
2 悬缆系统的动力学分析
垂挂高空平台上悬缆的物理模型,如图1所示。悬缆上端固定,底端的高空平台简化为一集中质量,悬缆受到的水平方向的外界激励等效为施加于悬缆中间位置的激励,悬缆中间位置的横向位移为。截取微小单元并进行受力分析,如图1(b)所示。
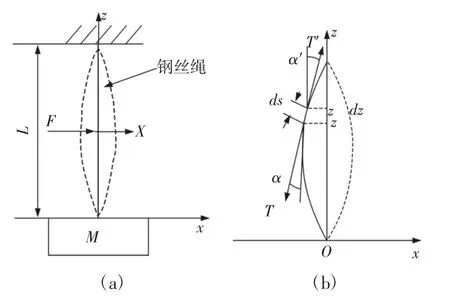
图1 悬缆的物理模型Fig.1 Physical Model of the Hoisting Cable
其微小单元ds在横向上的动力学方程为:

式中:T,T′—悬缆微元两端的张力;α,α′对应 T,T′跟垂直方向的夹角;cs—悬缆单位长度横向振动的阻尼系数;x—悬缆上任一点的振动位移,在高度位置为 z的处,x=x(z,t);ρ—悬缆的线密度。
忽略微元质量对张力的影响,可以认为张力是均匀的,即在(1)式中:。对悬缆在重负载的振动进行简化,有:
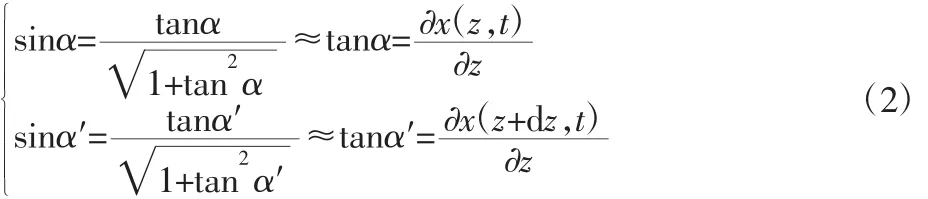
在悬缆的各阶振动模态中,对平台产生影响的主要是一阶模态,因而把一阶模态作为主要的抑振对象[10]。悬缆上任一点的一阶振动方程,如式(3)所示。

式中:X(t)—悬缆中点处的振幅;z—悬缆长度方向上的位置;L—悬缆的长度。悬缆上所有点的振动均与其重点的振动有关,所以建立悬缆振动模型以中点为参考点。把式(2)、式(3)代入式(1),考虑到悬缆受到的等效于中点的外界激励F′和主动抑振激励F,经整理可得式(4):

即为悬缆的运动学方程。式中:m—悬缆的总质量。F作为主动抑振激励,由模糊神经网络控制器提供,根据相应的控制算法,输出主动激励F,从而实现振动抑制效果。
3 模糊神经网络控制
通过前一节中对于悬缆进行模型建立,采用模糊神经网络控制对悬缆的振动进行控制。模糊控制之所以被广泛应用于控制中,是因为它更容易设计和理解。模糊控制中的隶属度函数的模糊化和模糊规则的推理都需要人为提前确定,不能实现自动调整参数,而神经网络的一大优点就是能够对其参数进行自适应调整,所以采用神经网络对模糊控制的逻辑规则进行记忆,将两种方法的优点结合设计控制系统并对高空悬缆进行抑振。
2.1 确定模糊参数
该文采用的模糊控制器是两个输入(E和EC)和一个输出(U),E和EC分别代表悬缆中点的位移和速度;输出U代表在悬缆中点处主动控制力。E、EC和U的模糊子集是{NB,NM,NS,ZO,PS,PM,PB}。隶属度函数为。利用曲线的两个参数与分辨率的关系,在MATLAB模糊控制箱中设定高斯函数参数,函数图,如图2所示。EC和U的隶属度函数图与E相同。

图2 E的隶属度函数Fig.2 The Membership Function of E
2.2 确定模糊控制规则
前面在悬缆的物理模型分析时,可以看出悬缆的振动曲线类比于正弦曲线,将整个过程分为四部分:第一部分中,将该部分为三个阶段,在第一阶段,位移较小且逐渐变大,速度最大且逐渐变小,应施加反向中等的控制力;在第二阶段,位移中等且逐渐变大,速度中等逐渐变小,应施加反向最大控制力;第三阶段,位移最大,速度最小,应施加反向最大控制力。其他三部分同理。模糊控制规则表,如表1所示。

表1 模糊控制规则表Tab.1 Fuzzy Control Rule Table
2.3 确实神经网络结构
第一层是输入层,Ii,Oi分别表示第一层的输入和输出。

第二层是模糊化层,将输入变量转化为相应的模糊量,方便模糊规则的建立。该层共有2×7=14个节点。

第三层是规则推理层,神经元数与规则数相等,共有7×7=49个。
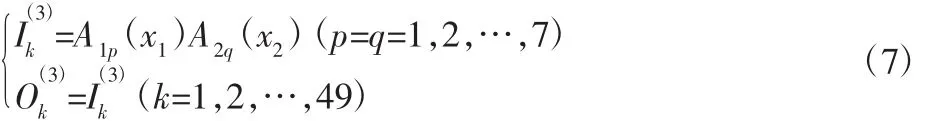
第四层是清晰化层,将输出的模糊量转为精确的输出量。

3 数值仿真及试验分析
3.1 高空悬缆的运动学模型
选取悬缆总长L为10m,线密度ρ为0.68kg/m,单位长度的阻尼系数cs为0.15,集中质量块的质量M为600kg,代入式(4)中,即可得到高空悬缆的振动方程。
3.2 模糊神经网络仿真
输入层有两个神经元分别代表钢丝绳中点处的振动位移和速度;输出层取一个神经元代表钢丝绳中点处的主动控制力的输出。训练样本数量为7×7=49组,如表2所示。
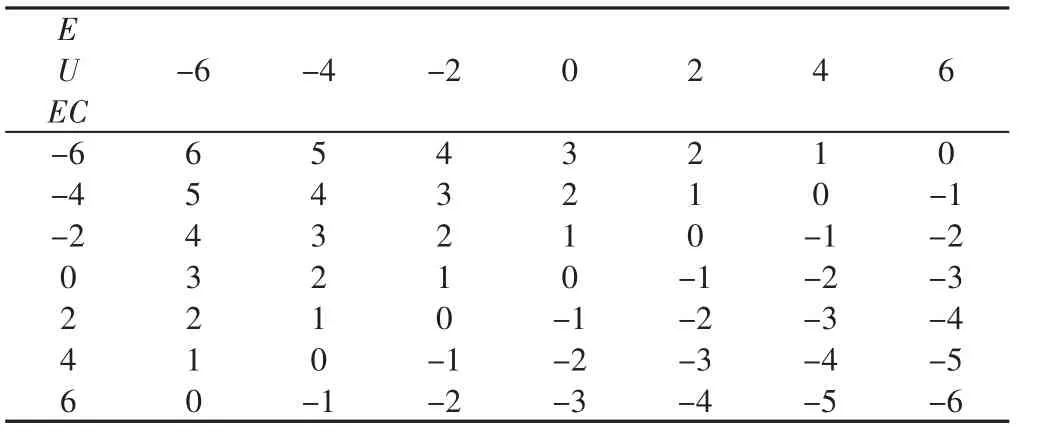
表2 训练样本Tab.2 Training Sample
通过一个4层的神经网络对模糊规则进行记忆,实质是对隶属度函数参数的调整,如表3所示。

表3 调整前后的隶属度参数Tab.3 Parameter of Membership Degree Before and After Adjustment

图3 悬缆中点处的横向振动位移响应Fig.3 Transverse Vibration Response for the Midpoint of Hoisting Cable
经过神经网络训练后的模糊控制规则免去了人为因素,针对实际的悬缆的振动情况,使模糊控制较之前的规则而言更合适。再利用其对悬缆振动的控制进行仿真,仿真时通过持续随机激励信号作用,在有控和无控状态下,仿真结果,如图3所示。从仿真结果可以看出,悬缆在未施加控制的情况下,悬缆中点处的位移响应幅值在(-3.37~3.58)cm之间;在控制情况下的位移响应幅值范围在(-0.88~0.94)cm。
3.3 试验分析
前面对高空悬缆进行抑振仿真分析,为了进一步验证模糊神经网络抑振方法的有效性,采取试验分析进行验证。以labview为操作平台进行测试。原理是压电加速度传感器获得高空悬缆的振动信号,电荷放大器将信号放大传至数据采集卡,进行模数转化传至PC,进行数据分析处理,通过电压放大器提供给电动式激振器合适的电压信号,使其对高空悬缆进行抑振。整体抑振测试系统,如图4所示。
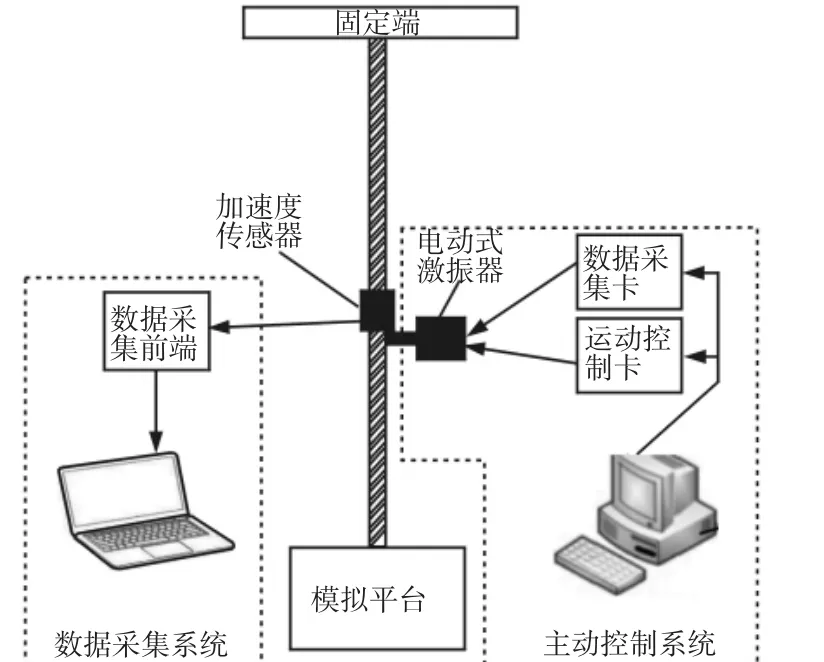
图4 抑振系统示意图Fig.4 Schematic Diagram of Vibration Suppression System
该系统选用凌华Nu-DAQ-2214数据采集卡,有16个AI通道,不仅具有模拟输入功能,还有2通道12位的模拟输出功能。同时具有模拟触发、数字触发以及24通道可编程数字I/O线及两通道16位通用计数器。选用型号为INV9822的加速度传感器,其技术参数为:灵敏度100mV/g,频率范围(0.5~8000)Hz。其原理是通过相对于高空悬缆垂线方向的变化来计算动静态的加速度,并通过二次积分得到振动位移变化。试验结果,如图5所示。从试验结果可以看出,高空悬缆在自由状态下的最大振幅约为3cm,施加模糊神经网络控制后,振动幅值大幅度降低,最大振幅约为0.9cm。

图5 主动抑振前后高空悬缆中点振动Fig.5 Median Vibration of High Aerial Hoisting Cable Before and After Active Vibration Suppression
5 结论
以幕墙安装高空平台为背景,针对高空悬缆在应用中的振动问题进行抑振方法的研究,概括为以下几点:
(1)截取悬缆的微元长度进行受力分析,考虑振动集中在低频段,只考虑一阶振型,进而推导出悬缆的运动学方程;(2)利用4层的BP网络对模糊规则进行记忆,设计了模糊神经网络控制测试系统,并对高空悬缆的振动进行MATLAB/simulink仿真,通过对比悬缆在无控和有控两种状态下的振动幅值曲线,可以得出悬缆中点的横向振动位移最大幅值被削减了大约72.4%;(3)进一步对高空悬缆在该控制方法下的抑振效果进行试验验证,建立了基于labview的测试系统,从测试结果看出,高空悬缆在控制前后振动的最大幅值分别约为3cm和0.9cm,振动削减了约70%,与仿真结果基本一致,所以该模糊神经网络控制方法对高空悬缆的抑振效果是很好的。对类似的结构中悬缆振动问题有较大的应用意义。
