天然气膨胀制冷工艺仿真优化
2020-04-28王泰人李耀龙
唐 慧,刘 云,王泰人,李耀龙
(1. 长江大学 石油工程学院 油气钻采工程湖北省重点实验室,湖北 武汉 430100;2. 湖北省天然气发展有限公司,湖北 武汉 430223)
在油气田开发过程中,为了达到天然气管输的烃露点标准和减少油气损耗,通常采用轻烃回收工艺来回收乙烷及以上重烃组分。常见的轻烃回收工艺是以冷凝回收法为主的液化加工技术[1-2]。轻烃回收不仅能提高企业效益,还能促进天然气产品的充分利用,通过轻烃回收可对天然气的热值进行调整[3]。天然气轻烃回收多采用以膨胀机制冷法为主的混合工艺[4-5]。通常采用深冷工艺,经透平式膨胀机膨胀制冷,物料降温程度大,轻烃回收率高[6-7]。目前,我国已经在部分油气田建设了膨胀制冷轻烃回收装置,但只有少数学者研究了膨胀制冷仿真模型[8-11]。由于等熵膨胀模型需调用等温闪蒸、等焓节流模型,包括很多迭代过程,如果初值不合适,很容易计算发散,因此需要改进模型的计算方法,解决模型计算的稳定性问题,提高模型计算效率。
本工作基于Benedict-Webb-Rubin-Starling(BWRS)状态方程,建立了天然气等熵膨胀制冷仿真模型,主要采用牛顿法、二分法、快速迭代法、弦截法或几种方法相结合的方法进行计算。通过实例计算表明,计算过程稳定,结果误差小,并通过优化计算研究了压力、温度和膨胀机效率等对轻烃回收率的影响。建立的模型和求解方法可用于天然气等熵膨胀计算,为轻烃回收系统流程仿真模拟和优化奠定了基础。
1 实验部分
1.1 状态方程的选择
可应用的状态方程有很多种,但对于接近露点、气体和液体都具良好适用性的真实流体方程主要有Soave-Redlich-Kwong(SRK),Peng-Robinson(PR),BWRS 等状态方程。其中,BWRS 状态方程应用范围较广、精度较高,用于气态和液态模拟的同时亦可用于气液混合状态下的模拟计算状态方程可应用于很宽的温度和密度范围,首选该方程为天然气轻烃回收计算的状态方程[13-14],见式(1)。
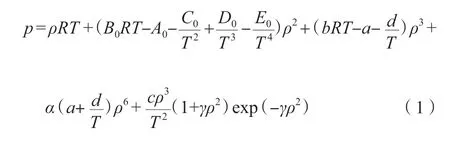
式中,p 为系统压力,kPa;ρ 为气相或液相的密度,kg/m3;T 为系统温度,K;R 为气体常数,8.314 3 kJ/(kmol·K);A0,B0,C0,D0,E0,γ,a,b,c,d,α 为非固定值参数,与各组分的密度、摩尔分数、偏心因子及二元交互系数相关[15-16]。
1.2 等熵膨胀数学模型的建立
1.2.1 等熵膨胀过程
等熵膨胀过程是天然气以自身为介质通过绝热膨胀机,在气体减压的同时绝热降温,自身温度下降。由于降温,一部分露点低的组分凝结成液,以达到纯化天然气的目的。首先选择物料组分,设定压力、温度、组分摩尔分数、熵、焓。经过等熵膨胀制冷设备后,根据膨胀后物料的压力计算膨胀终温。不同温度下可得到不同压力、熵、焓、气液比及气液相各组分含量。
天然气等熵膨胀过程计算较复杂,不仅需计算状态方程中的参数,还需计算天然气物性参数,如混合密度、逸度、压缩系数、比热容、焓、熵、相平衡常数、气化率、泡点露点、偏心因子、临界偏心因子等。
1.2.2 等熵膨胀过程的参数计算
1.2.2.1 密度的计算
密度是物性计算中的基本参数,根据指定的p,T 和混合物组成(xi,yi)用BWRS 状态方程求解气相密度(ρV)或液相密度(ρL)。二分法、弦截法、牛顿法均可用于天然气混合密度的计算。牛顿法和弦截法的迭代次数少、收敛速度快,优于二分法,然而运用牛顿法解决问题的过程中,需要同时计算密度函数和密度函数的导数,牛顿法计算函数值的次数高于弦截法,所以,无需求导数的弦截法是计算天然气混合物密度的一个必然选择[17]。
以ρ 为变量的BWRS 方程见式(2)。
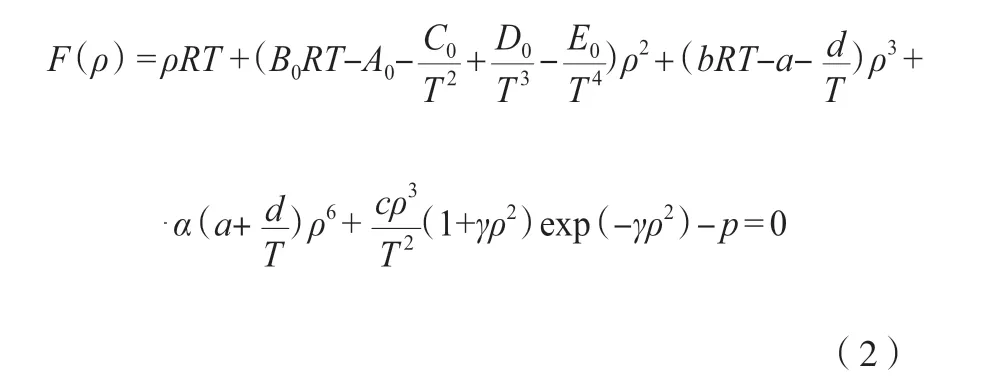
指定T,p,xi,yi,当F(ρ)=0 时,弦截法迭代求ρ,见式(3)。
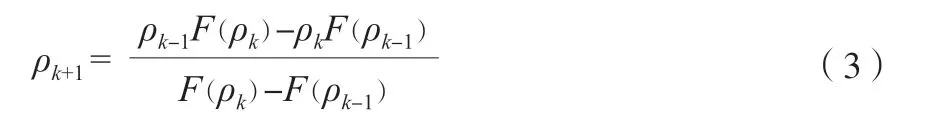
式中,下标k 表示迭代次数。
按所设初值ρV和ρL分别由BWRS 方程求出F(ρ1)和F(ρ2)后,便可由弦截法的迭代公式依次求定下一次迭代用ρ。迭代计算进行至︱ρk+1-ρk︱≤ερ(ερ为允许误差)为止。当取ερ=10-4时,对ρV一般仅需迭代3 ~6 次,而求解ρL时一般则需迭代6 ~18 次。
1.2.2.2 压缩因子的计算
天然气处理过程中需考虑气体的压缩性,结合实际情况使计算结果满足计算精度的要求。基于BWRS 状态方程,压缩因子(Z)的计算见式(4)。
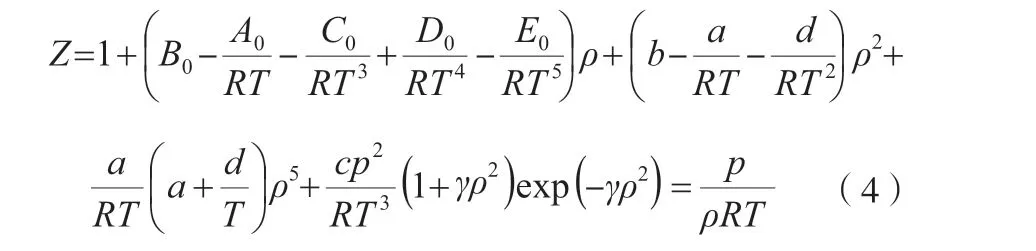
密度由式(2)迭代计算所得。混合物密度计算相当重要,后续参数(如逸度、比热容、泡点、露点等)计算仍需调用密度值。
1.2.2.3 气化率的计算
部分气化或部分冷凝过程的基本方程式见式(5)~式(9)。
相平衡方程:
yi= Kixi1≤i ≤n (5)气液相组成和归一化方程:

物料平衡方程:
Fzi= Vyi+ Lxi(7)
F = V + L (8)
式中,F 为进料量,kmol/h;zi为液相或气相进料组成(摩尔分数);V,L 分别为进料经加热或冷却至温度T,部分气化或部分冷凝后进入分离器(压力为p),分离成平衡的气、液两相的量,kmol/h;xi为液相组成(摩尔分数);yi为气相组成(摩尔分数);Ki为i 组分的平衡常数。
气化率(e)按式(9)计算。
e = V/F (9)
联立式(4)~式(7)可得等熵膨胀过程的基本方程式(10)。
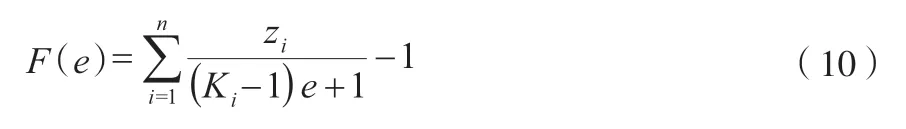
为了防止运行故障,本工作采用牛顿法和二分法相结合的方法求解,在求解非线性方程的同时又提高了运行速度。根据已求得的ek先用牛顿迭代法求解ek+1,若迭代速度慢或ek+1不在预定解区间,则用二分法继续运算,直到得到满足要求的解为止。
1.2.3 等熵膨胀模型
对于实际混合气体的熵可按式(13)计算。
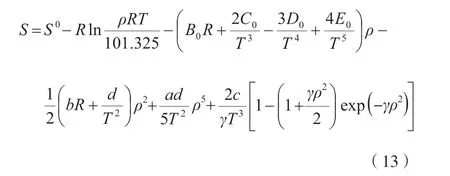
部分气化或部分冷凝的计算一般是已知F,zi,p,T,求e,yi,xi。采用一个经常可获得快速收敛而对e 的初值无特殊要求的目标函数F(e)。令
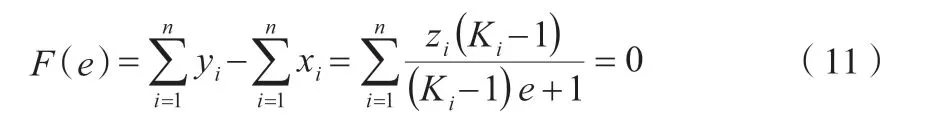
一般F(e)=0 是非线性方程,可用牛顿迭代法求解,迭代公式见式(12)。
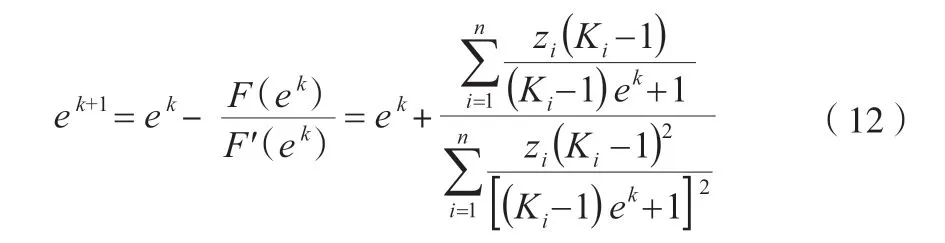
式中,迭代收敛条件为︱F(ek+1)︱≤ε;k 为迭代次数;ε 为预先给定好的足够小的正数。
在计算过程中应先判断原料混合物在给定T,p 下的状态是否处于两相区,由于平衡常数Ki是未知的,需要假设初值,此计算方法不做赘述,具体参照Antoine 方程来计算。
式中,S 为气相或液相混合物的实际熵,kJ/(kmol·K);S0为理想混合气体的熵,kJ/(kmol·K)。
等熵膨胀过程[18]基本计算方程见式(14)~式(19)。
热平衡方程:

膨胀过程(等熵条件下)所产生的理想功(WS):
Ws= ΔHs= HF- HI(16)
膨胀过程所产生的实际功(W):
W = ΔH = ηsWs= ηsΔHs(17)
膨胀机实际出口焓:
HF= HI- ΔH (18)
膨胀机绝热效率(ηS):

式中,SI,SF 分别为膨胀机膨胀前后的熵,kJ/(kmol·K);SV,SL 分别为膨胀机膨胀后平衡气相和液相的熵,kJ/(kmol·K);HI,HF 分别为膨胀机膨胀前后的焓,kJ/kmol;pI,pF 分别为膨胀机膨胀前后的压力,kPa;TI,TF 分别为膨胀机膨胀前后的温度,K;β 为多变指数,对天然气取1.35 ~ 1.4;ΔH 为膨胀机前后气体的实际焓降;ΔHS 为膨胀机绝热焓降。实际情况下,任何膨胀设备都不可能达到完全绝热,空分装置的透平膨胀机的等熵效率一般在80% 左右。
1.2.4 计算流程框图
图1 为等熵膨胀制冷计算流程。
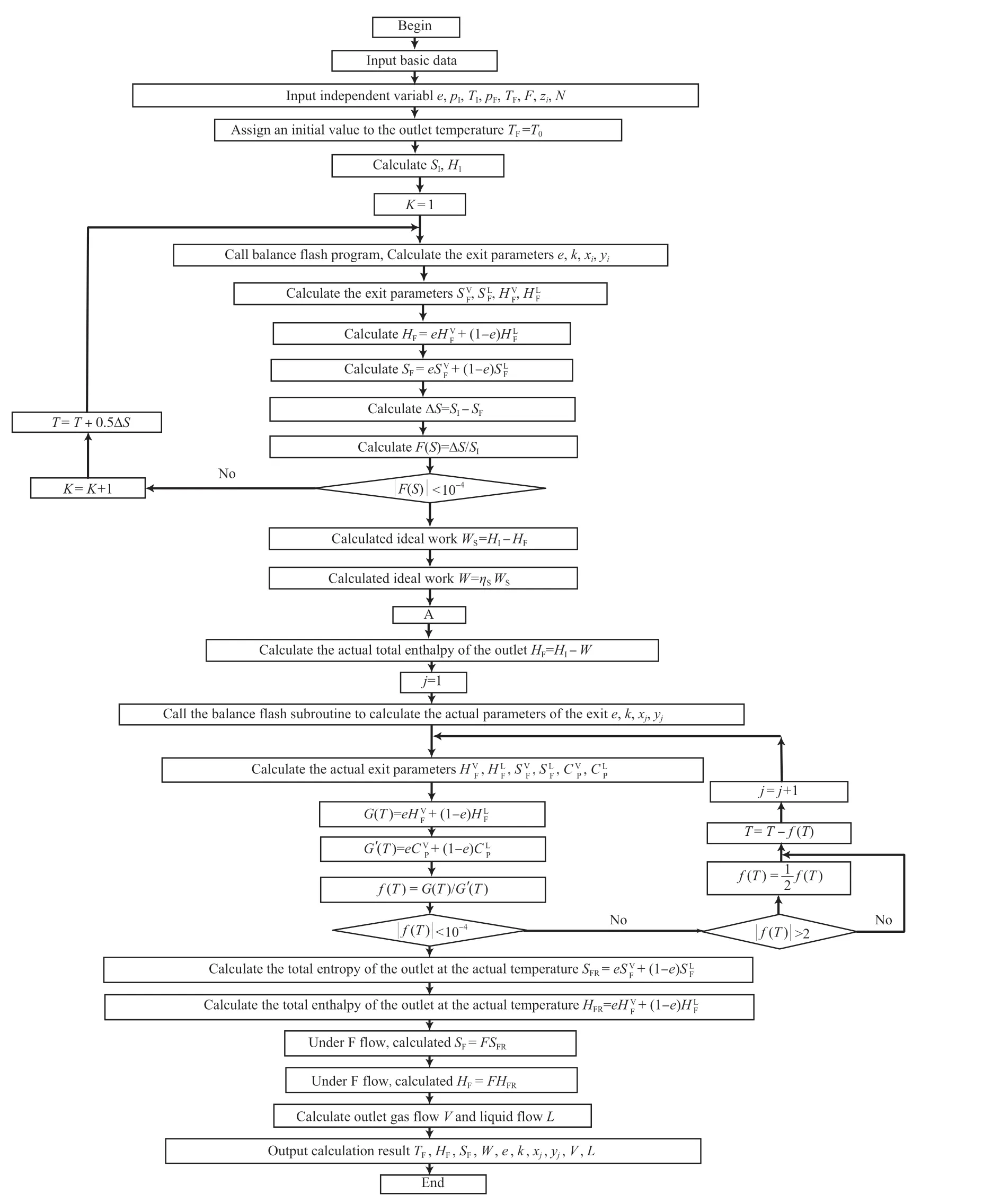
图1 等熵膨胀计算流程Fig.1 Isentropic expansion calculation process.
由图1 可知,输入基础数据时,首先应选择物料组分,其中包括选择烃类物质和非烃类物质(H2O,H2S,CO2),输入独立变量参数,出口温度需设定初值。在以上参数的基础上计算初始焓和熵。等熵膨胀算法模拟是在等温闪蒸算法的基础上建立起来的,需调用等温平衡闪蒸程序[19]计算出口理想的物性参数。当绝对误差小于0.000 1,满足等熵膨胀的要求时,软件继续运行计算;否则,以步长为0.5ΔS 的温变进行试算,直到误差满足要求为止。此次循环计算得出经膨胀机后做的实际功、实际出口总焓、实际出口温度。计算出实际出口温度后,再次调用等温平衡闪蒸程序计算出口实际温度下的物性参数。在输出实际出口总焓前,采用牛顿迭代法对函数G(T)进行核算,确保实际出口温度与该温度下焓的反推温度一致。在此计算过程中如果f(T)数值较大,则以f(T)/2 为迭代步长,能减少计算步骤,迅速收敛[20]。
2 实例验证及优化
本工作在上述等熵膨胀的理论和方法基础上,结合等温闪蒸计算程序,以VC 为前台应用程序,Microsoft Access 为后台数据库,采用ADO 编程接口访问属性数据,研制了等熵膨胀过程模拟软件。软件的功能模块除了含有物质物性参数模块和等温闪蒸模块外,还补充了等熵膨胀模块。在等熵膨胀计算模块输入物料及组分、初始温度、初始压力、膨胀终压,即可计算膨胀终温。计算结果可显示在表格中,清楚明了。等熵膨胀模型包括多个子程序,如求BWRS 方程11 个参数的子程序、求气相或液相密度根的子程序、求焓/熵的子程序、相平衡常数子程序等。各个子程序的独立存在使等熵膨胀模型功能模块化,易于开发人员理解和改善,通过主程序的管理和子程序的运行,使等熵膨胀模型准确高效地运行。
为了检验软件的可靠性,引用实例验证。表1为文献数据和软件计算数据对比。由表1 可知,与文献数据对比,三组数据的绝对误差分别为1.12,0.84,3.11,相对误差分别为0.005 43,0.003 98,0.019 27,均小于0.02,可认为计算结果真实有效,本软件可用于燃气等熵膨胀过程计算模拟。
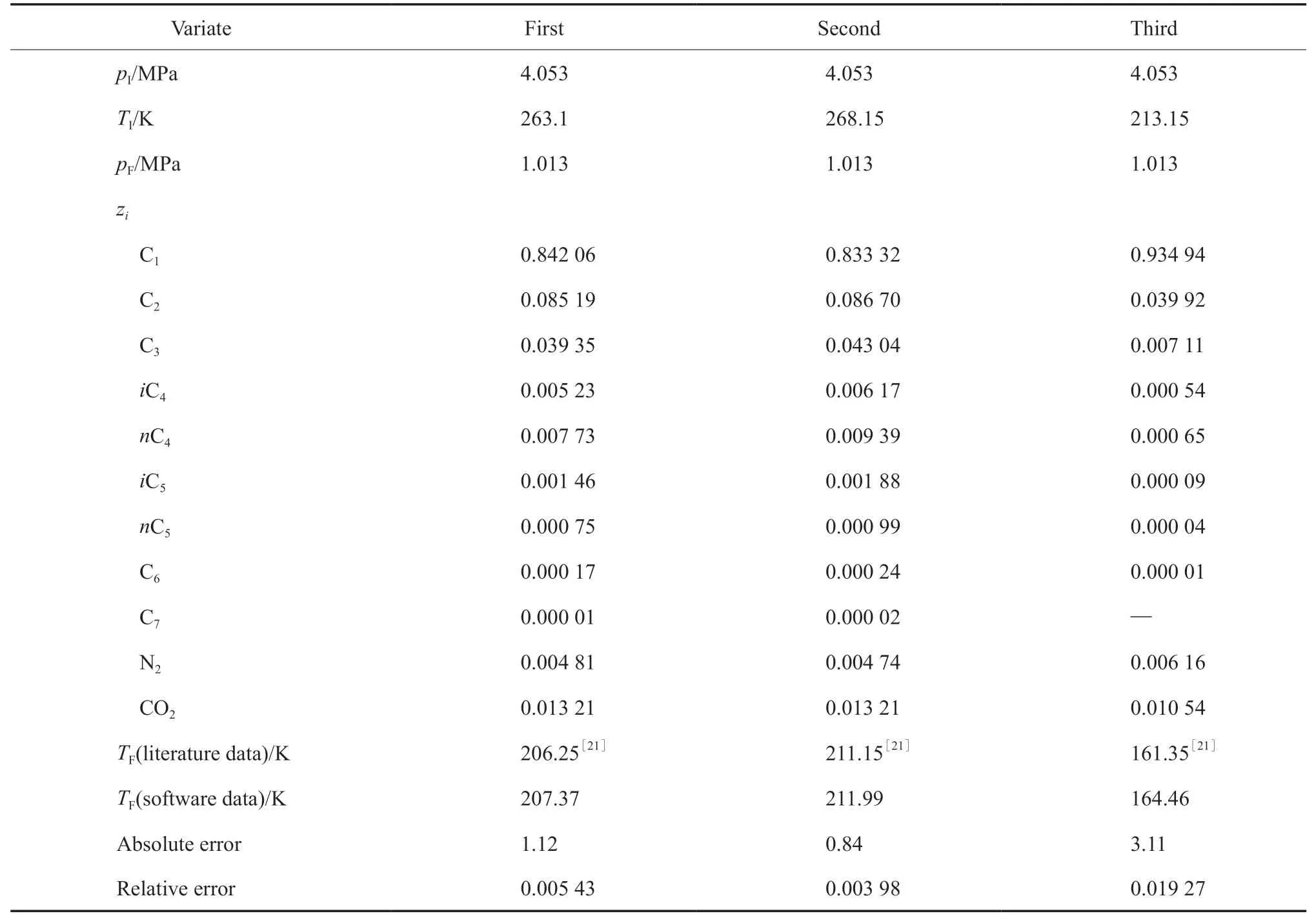
表1 文献数据和软件计算数据对比Table 1 Comparison between literature data and software calculation data
3 结论
1)在等温闪蒸模拟计算的基础上研发了等熵膨胀计算软件。软件基于BWRS 状态方程,利用弦截迭代法计算实际混合气体密度,以牛顿迭代法计算实际出口温度,利用二分法快速收敛。多种迭代方法结合计算可简化计算过程、提高计算速度。
2)与文献数据对比,三组数据的绝对误差分别为1.12,0.84,3.11,相对误差分别为0.005 43,0.003 98,0.019 27,均小于0.02,可认为计算结果真实有效,软件可用于天燃气等熵膨胀过程计算模拟。
3)等熵膨胀计算过程繁杂,手工计算或借用Excel 表格计算都不是最好的选择。软件隐藏计算程序,操作界面简明、方法简单,便于初学者学习,同时可为后续轻烃回收软件开发提供技术参考。
符 号 说 明
A0,B0,C0,D0,E0,γ,a,b,c,d,α
非固定值参数,与各组分的密度、摩尔分数、偏心因子及二元交互系数相关
e 气化率
F 进料量,kmol/h
f 逸度系数
H 焓值,kJ/kmol
ΔH 膨胀机前后气体的实际焓降,kJ/kmol
ΔHS膨胀机绝热焓降,kJ/kmol
Kii 组分的相平衡常数
k 迭代次数
L 液相的量,kmol/h
p 系统压力,kPa
R 气体常数, 8.314 3 kJ/(kmol·K)
S 气相或液相混合物的实际熵,kJ/(kmol·K)
S0理想混合气体的熵,kJ/(kmol·K)
T 系统温度,K
V 气相的量,kmol/h
W 理想功,kJ
WS实际功,kJ
xi气相组成,摩尔分数
yi液相组成,摩尔分数
Z 压缩因子
zi进料组成,摩尔分数
β 多变指数,对天然气取1.35 ~1.4
ε 预先给定好的足够小的正数
εp允许误差
ηS膨胀机绝热效率
ρ 气相或液相的密度,kg/m3
上标
L 平衡液相
V 平衡气相
下标
F 经膨胀机膨胀后
I 经膨胀机膨胀前
