随机变量的期望与方差的求法初探

■湖北省黄梅县小池滨江高级中学

随机变量是高考的必考内容,其中离散型随机变量的概率分布列与期望、方差是热点,题型以解答题为主,以选填题为辅。高考对这部分内容的考查贴近生活,注重考查基础知识和基本方法。在计算随机变量的期望和方差时,首先要搞清其分布特征及分布列,然后要准确应用公式,只有充分利用其性质,才能避免烦琐的运算,提高运算速度和准确度。

考点一 离散型随机变量的期望与方差

例1在北上广等十余所大中城市中,一款叫“一度用车”的共享汽车给市民们提供了一种新型的出行方式。2020年,黄冈市也将出现共享汽车,用户每次租车时按行驶里程(1元/km)加用车时间(0.1元/min)收费。李先生家离上班地点10 km,每天租用共享汽车上下班,由于堵车原因,每次路上开车花费的时间是一个随机变量,根据一段时间统计40 次路上开车花费时间在各时间段内的情况得到表1：

表1

视各时间段发生的频率为概率,假设把每次路上开车花费的时间视为用车时间,范围为[15,65]min。

(1)若李先生上下班时租用一次共享汽车路上开车不超过45 min,便是所有可选择的交通工具中的一次最优选择,设ξ是4 次使用共享汽车中最优选择的次数,求ξ的分布列和期望;

(2)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表)?

解析：(1)李先生每次租用共享汽车为最优选择的概率P=。

依题意ξ的值可能为0,1,2,3,4,且ξ～,P(ξ=1)=,P(ξ=2)=,P(ξ=3)=,P(ξ=4)=。

故ξ的分布列如表2：

表2

(2)每次用车路上平均花的时间：

每次租车的费用约为10+35.5×0.1=13.55(元)。

一个月的平均用车费用约为13.55×20×2=542(元)。

点评：二项分布解决的问题是独立重复试验,“重复”的意思是每次事件发生的概率相等,也可以在若干次的放回抽样中求概率,每一次抽样结果都有两个：发生或不发生,而且事件发生与否的概率在每一次独立试验中都保持不变,即每次是等概率的,前一次不影响后一次的概率。若放回或不放回较难区分时,一般可通过数量来区分,从总体中抽取或数量较多时抽取一般为二项分布。

例2自由购是一种通过自助结算的购物形式。某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理得到表3：

表3

(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率。

(2)从被抽取的年龄在[50,70]使用自由购的顾客中,随机抽取3人进一步了解情况,用X表示这3 人中年龄在[50,60)的人数,求随机变量X的分布列及数学期望。

(3)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋。若某日该超市预计有5 000 人购物,试估计该超市当天至少应准备多少个环保购物袋。

解析：(1)随机抽取的100 名顾客中,年龄在[30,50)且未使用自由购的有3+14=17(人),故随机抽取1名顾客,该顾客年龄在[30,50)且未参加自由购的概率估计为P=。

(2)X所有的可能取值为1,2,3。

故X的分布列如表4：

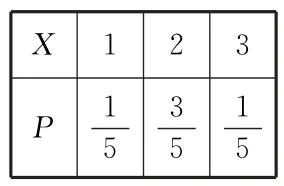
表4

则E(X)==2。

(3)随机抽取的100名顾客中,使用自由购的有3+12+17+6+4+2=44(人),则该超市当天至少应准备环保购物袋的个数为×5 000=2 200。

点评：超几何分布是知道总体的个数N的一种不放回抽样中求概率情形,其抽样中每一次抽样结果有两个：发生或不发生,但每次的概率是不相等的,前一次会影响后一次的概率。一般在数目不是很大的情况下,利用二项分布和超几何分布公式计算期望值会不同,但抽取对象数目较大时,两者计算的期望值会近似相等。另外,当总体的数量很大时,应用超几何分布解决问题时计算量会非常大,所以当总体的数量很大时,在误差允许的范围内,我们可以用二项分布来代替超几何分布。

考点二 独立事件的期望与方差

例3电影公司随机收集了电影的有关数据,经分类整理得到表5：

表5

好评率是指：一类电影中获得好评的部数与该类电影的部数的比值。假设所有电影是否获得好评相互独立。

(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;

(2)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用“ξk=1”表示第k类电影得到人们喜欢,“ξk=0”表示第k类电影没有得到人们喜欢(k=1,2,3,4,5,6),写出方差D(ξ1),D(ξ2),D(ξ3),D(ξ4),D(ξ5),D(ξ6)的大小关系。

解析：(1)由题意知,样本中电影的总部数是140+50+300+200+800+510=2 000。

第四类电影中获得好评的电影部数是200×0.25=50,故概率P==0.025。

(2)由题意知,定义随机变量如下,ξk=

则ξk～(0,1)服从两点分布,则六类电影的分布列及方差计算如下：

第一类电影,E(ξ1)=1×0.4+0×0.6=0.4,D(ξ1)=(1-0.4)2×0.4+(0-0.4)2×0.6=0.24;

第二类电影,E(ξ2)=1×0.2+0×0.8=0.2,D(ξ2)=(1-0.2)2×0.2+(0-0.2)2×0.8=0.16;

第三类电影,E(ξ3)=1×0.15+0×0.85=0.15,D(ξ3)=(1-0.15)2×0.15+(0-0.15)2×0.85=0.127 5;

第四类电影,E(ξ4)=1×0.25+0×0.75=0.25,D(ξ4)=(1-0.25)2×0.25+(0-0.25)2×0.75=0.187 5;

第五类电影,E(ξ5)=1×0.2+0×0.8=0.2,D(ξ5)=(1-0.2)2×0.2+(0-0.2)2×0.8=0.16;

第六类电影,E(ξ6)=1×0.1+0×0.9=0.1,D(ξ6)=(1-0.1)2×0.1+(0-0.1)2×0.9=0.09。

故D(ξ1)＞D(ξ4)＞D(ξ2)=D(ξ5)＞D(ξ3)＞D(ξ6)。

点评：第一问用古典概型的概率计算公式直接求解,第二问先判断ξk～(0,1)服从两点分布,再利用离散型随机变量的期望和方差公式,分别求出这6个随机变量的期望与方差。

考点三 连续型随机变量的期望

例4某地区将一种新品种小麦在一块试验田进行试种。从试验田中抽取500株小麦,测量这些小麦的生长指标值,由测量结果得到频数分布表(表6)：

表6

(2)由直方图可以认为,这种小麦的生长指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数,σ2近似为样本方差s2。

①利用该正态分布,求P(187.8＜Z＜212.2) ;

②若从试验田中抽取100株小麦,记X表示这100 株小麦中生长指标值位于区间(187.8,212.2)的小麦株数(四舍五入),利用①的结果,求E(X)。

解析：(1)抽取小麦的生长指标的样本平均数和样本方差s2分别为：

(2)①由上知Z～N(200,150),故P(187.8＜Z＜212.2)=P(200-12.2＜Z＜200+12.2)=0.682 6。

②由①知,一株小麦的生长指标值位于区间(187.8,212.2)的概率为0.682 6,依题意知X～B(100,0.682 6),所以E(X)=100×0.682 6=68.26≈68。

例5从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图1 所示的频率分布直方图,质量指标值落在区间[55,65],[65,75],[75,85]内的频率之比为4∶2∶1。

(1)求这些产品质量指标值落在区间[75,85]内的频率;

(2)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间[45,75]内的产品件数为X,求X的分布列与数学期望。

解析：(1)设落在区间[75,85]内的频率为x,则落在区间[55,65],[65,75]内的频率分别为4x,2x,依题意得(0.004+0.012+0.019+0.03)×10+4x+2x+x=1,解得x=0.05。落在区间[75,85]内的频率为0.05。

(2)从该企业生产的该种产品中随机抽取3件,相当于进行了3次独立重复试验,所以X服从二项分布B(n,p),其中n=3。由(1)得,落在区间[45,75]内的频率为0.3+0.2+0.1=0.6,将频率视为概率得p=0.6。

因为X的所有可能取值为0,1,2,3,且P(X=0)=×0.60×0.43=0.064,P(X=1)=×0.61×0.42=0.288,P(X=2)=×0.62×0.41=0.432,P(X=3)=×0.63×0.40=0.216。

所以X的分布列如表7：

表7

所以X的数学期望为E(X)=0×0.064+1×0.288+2×0.432+3×0.216=1.8。

也可直接根据二项分布的均值公式得到E(X)=np=3×0.6=1.8。

点评：每一个条形图的面积对应的就是该段产品的频率,若独立重复试验结果服从二项分布,可以直接由公式得出数学期望。

总结归纳：

1.求离散型随机变量的均值与方差的步骤：(1)确定随机变量ξ的所有可能值;(2)写出每一个随机变量所对应的概率;(3)列出随机变量的概率分布列;(4)根据定义求出均值E(ξ)和方差D(ξ);(5)由均值、方差进一步分析判断,得出结论。

2.要注意观察随机变量的概率分布特征,若如果ξ～B(n,p),则用公式E(ξ)=np,D(ξ)=np(1-p)求解,可大大减少计算量。有些随机变量虽不服从二项分布,但与之具有线性关系的另一随机变量服从二项分布,可以综合应用E(aξ+b)=aE(ξ)+b以及D(aξ+b)=a2D(ξ)。

3.预计2020年将会考查：①离散型随机变量的期望与方差,通过设置密切贴近现实生活的情形,考查概率思想的应用意识和创新意识;②正态分布的考查,尤其是正态总体在某一区间内的概率。此类题型为解答题中的一问,试题难度不会太大,属中档题型。