统计与概率的综合例说

■山东省枣庄二中

概率是近几年高考的热点之一,主要考查随机事件的概率、古典概型、几何概型、随机变量及其分布等知识,近几年高考对概率的考查由单一型向知识交汇型转变,且多为古典概型、随机变量及其分布与茎叶图、频率分布直方图、回归分析、独立性检验等交汇考查。

一、古典概型与独立性检验的交汇考查

例1(2019 年高考新课标Ⅰ卷文数)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到列联表：

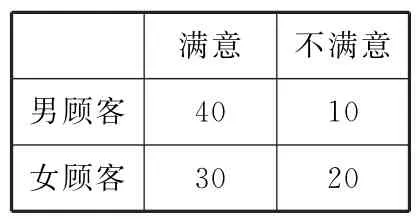
表1

(1)分别估计男、女顾客对该商场服务满意的概率;

(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?

附：K2=。

表2

解析：从题中所给的2×2列联表中读出相关的数据,利用满意的人数除以总的人数,分别算出相应的频率,即估计得出的概率值;利用公式求得观测值与临界值比较,得到能有95%的把握认为男、女顾客对该商场服务的评价有差异。

(1)由题中表格可知,50 名男顾客中对商场服务满意的有40人,所以男顾客对商场服务满意率估计为。

50名女顾客中对商场满意的有30 人,所以女顾客对商场服务满意率估计为P2=。

(2)由列联表可知K2=≈4.762 ＞3.841,所以能有95%的把握认为男、女顾客对该商场服务的评价有差异。

点睛：解答此类问题的策略：(1)解决古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;当基本事件总数较少时,可用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助表格,树状图列举,同时注意判断是古典概型还是几何概型,基本事件前者是有限的,后者是无限的。

(2)独立性检验是用来考查两个分类变量是否有关系,计算随机变量的观测值K2,K2越大,说明两个分类变量有关系的可能性越大。

该题考查的是有关概率与统计的知识,涉及的知识点有利用频率来估计概率,利用列联表计算K2的值,独立性检验,属于简单题目。

二、古典概型与用样本估计总体交汇考查

例2(贵州省2019届高三联考试题)随机抽取某校高一100名学生的期末考试英语成绩(他们的英语成绩都在80分～140分之间),将他们的英语成绩(单位：分)分成：[80,90),[90,100),[100,110),[110,120),[120,130),[130,140]六组,得到如图1所示的部分频率分布直方图,已知成绩处于[90,100)内与[100,110)内的频数之和等于成绩处于[110,120)内的频数,根据图中的信息,回答下列问题：

(1)求频率分布直方图中未画出的小矩形的面积之和;

(2)求成绩处于[110,120)内与[100,110)内的频率之差;

(3)用分层抽样的方法从成绩不低于120分的学生中选取一个容量为6 的样本,将该样本看成一个总体,从中任选2人,求这2人中恰有1人成绩低于130分的概率。

解析：(1)由题意可知,成绩处于[110,120)内的概率为1-(0.010+0.015+0.025+0.005)×10=0.45,所以频率分布直方图中未画出的小矩形的面积之和为0.45。

(2)设成绩处于[100,110)与[110,120)内的频率分别为a,b。

因为成绩处于[90,100)内与[100,110)内的概率之和等于成绩处于[110,120)内的频率,所以：

所以成绩处于[110,120)内与[100,110)内的频率之差为0.3-0.15=0.15。

(3)由题意知,成绩处于[120,130)内的学生数为100×0.25=25,成绩处于[130,140)内的学生数为100×0.05=5。所以用分层抽样的方法从身高不低于120分的学生中选取一个容量为6 的样本,需从成绩处于[120,130)内的学生中选取5人,记为A,B,C,D,E;从成绩处于[130,140)内的学生中选取1 人,记为F。从中任选2 人：(AB),(AC),(AD),(AE),(AF),(BC),(BD),(BE),(BF),(CD),(CE),(CF),(DE),(DF),(EF)共有15种情况,这2人中恰有1人成绩低于130 分的共有5 种情况,这2 人中恰有1人成绩低于130分的概率P==。

点睛：求解此类问题的三步骤：

(1)识图,即能读懂已知频率分布直方图或茎叶图所隐含的信息并进行信息提取。

(2)转化,即对文字语言较多的题,需要根据题目信息耐心阅读,步步实现文字语言与符号语言间的转化。

(3)计算,即对频率分布直方图或茎叶图所反馈的信息进行提取,并结合古典概型的概率公式进行运算。

三、随机变量及其分布与用样本估计总体交汇考查

例3(广西百色市高三年级2019 届摸底调研)在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品进行改良,为了检查改良效果,从中随机抽取100件作为样本,称出它们的重量(单位：g),重量分组区间为[10,20],(20,30],(30,40],(40,50],由此得到样本的重量频率分布直方图(如图2)。

(1)求a的值;

(2)根据样本数据,估计样本中个体的重量的众数与平均值;

(3)以样本数据来估计总体数据,从改良的农产品中随机抽取3 个个体,其中重量在[10,20]内的个体的个数为X,求X的分布列和数学期望。(以直方图中的频率作为概率)

解析：(1)由题意,得(0.020+0.032+a+0.018)×10=1,解得a=0.030。

(2)由最高矩形所对应区间中点的横坐标为25,可估计样本个体重量的众数约为25g。而100 件样本重量的平均值为x=0.2×15+0.32×25+0.3×35+0.18×45=29.6(g),故估计样本中个体重量的平均值约为29.6g。(3)利用样本估计总体,该样本中个体的重量在[10,20]内的概率为0.2,则X～。

故X的分布列如表3：

表3

则E(X)=。

点睛：本题考查了利用频率直方图求平均数与众数和概率的计算,也考查了二项分布,是中档题。

四、古典概型与随机变量及其分布的交汇考查

例4(河北省唐山市2019 届高三摸底考试数学试题)甲、乙两位工人分别用两种不同工艺生产同一种零件,已知尺寸在[223,228](单位：mm)内的零件为一等品,其余为二等品,测量甲、乙当天生产零件尺寸的茎叶图如图3所示：

(1)从甲、乙两位工人当天所生产的零件中各随机抽取1个零件,求抽取的2个零件等级互不相同的概率;

(2)从工人甲当天生产的零件中随机抽取3个零件,记这3个零件中一等品数量为X,求X的分布列和数学期望。

解析：(1)由茎叶图可知,甲当天生产了10个零件,其中4 个一等品,6 个二等品;乙当天生产了10个零件,其中5个一等品,5个二等品。所以抽取的2个零件等级互不相同的概率P=。

(2)X可取0,1,2,3。

X的分布列如表4：

表4

因此,E(X)=。

点睛：本题主要考查古典概型概率公式以及离散型随机变量的分布列与数学期望,属于中档题。求解数学期望问题,首先要正确理解题意,其次要准确无误地找出随机变量的所有可能值,计算出相应的概率,写出随机变量的分布列,正确运用期望、方差的公式进行计算,也就是要过三关：(1)阅读理解关;(2)概率计算关;(3)公式应用关。