求离散型随机变量期望与方差的常见策略
2020-04-28江苏省盐城市时杨中学
■江苏省盐城市时杨中学
离散型随机变量最重要的特征数是数学期望与方差,反映了随机变量取值的平均水平与波动幅度,它们都是建立在分布列基础之上,与概率相联系,因而成为高考的重点。通常情况下,求解离散型随机变量的数学期望与方差,都是先求出随机变量取每个值时的概率,再得其分布列,最后用数学期望与方差的定义求解。
一、利用离散型随机变量的期望与方差的定义求解
例1(2019年北京理数第17题)改革开放以来,人们的支付方式发生了巨大转变,近年来,移动支付已成为主要支付方式之一。为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如表1:

表1
(1)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率。
(2)从样本中仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1 000元的人数,求X的分布列和数学期望。
(3)已知上个月样本中学生的支付方式在本月没有变化,现从样本中仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于 2 000。根据抽查结果,能否认为样本中仅使用A的学生中本月支付金额大于2 000的人数有变化? 请说明理由。
解析:(1)由题意知,从全校所有的1 000名学生中随机抽取的100人中,A,B两种支付方式都不使用的有5人,仅使用A的有30人,仅使用B的有25 人,故A,B两种支付方式都使用的人数为100-5-30-25=40。
则从全校学生中随机抽取1 人,估计该学生上个月A,B两种支付方式都使用的概率。
(2)从样本中仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1 000元的人数,则X的可能取值为0,1,2。样本中仅使用A的学生有30人,其中支付金额在(0,1 000]的有18人,超过1 000元的有12人。样本中仅使用B的学生有25 人,其中支付金额在(0,1 000]的有10人,超过1 000元的有15人。
故X的分布列如表2:

表2
(3)不能认为样本中仅使用A的学生中本月支付金额大于2 000 元的人数有变化,理由如下:从样本知仅使用A的学生有30人,其中27人月支付金额不大于2 000,有3人月支付金额大于2 000,随机抽查3 人,发现他们本月的支付金额都大于2 000的概率为,但也有发生的可能。
故不能认为样本中仅使用A的学生中本月支付金额大于2 000的人数有变化。
点评:本题考查概率、离散型随机变量的分布列、数学期望的求法,又考查古典概型、相互独立事件概率乘法公式等基础知识,也考查同学们的推理能力与计算能力,是中档题。
练习1:某市有甲、乙、丙3个旅游景点,一位客人游览这3个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
(1)求ξ的分布列及数学期望;
(2)记“函数f(x)=x2-3ξx+1在区间[2,+∞)上单调递增”为事件A,求事件A的概率。
解析:用A1表示游览了第一个景点,表示没游览第一个景点;A2表示游览了第二个景点,表示没游览第二个景点;A3表示游览了第三个景点,表示没游览第三个景点。
(1)由分析得,P(ξ=3)=P(A1·A2·A3)+=P(A1)·P(A2)·P(A3)+=2×0.4×0.5×0.6=0.24。
P(ξ=1)=1-0.24=0.76。
所以ξ的分布列如表3:

表3
故E(ξ)=1×0.76+3×0.24=1.48。
(2)因为f(x)=,所以 函 数f(x)=x2-3ξx+1 在区间上单调递增。要使f(x)在[2,+∞)上单调递增,当且仅当,即ξ≤。从而P(A)==P(ξ=1)=0.76。
二、利用特殊分布的数学期望与方差求解
例2(2019 年天津理16)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为。假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立。
(1)用X表示甲同学上学期间的3天中7:30之前到校的天数,求随机变量X的分布列和数学期望;
(2)设M为事件“上学期间的3天中,甲同学在7:30 之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M发生的概率。
解析:(1)甲同学上学期间的3天中到校情况相互独立,且每天7:30之前到校的概率均为,故X~,从而P(X=k)=。
X的分布列如表4:

表4
(2)设乙同学上学期间的3天中7:30到校的天数为Y,则Y~。
由题意知M={X=3,Y=1}∪{X=2,Y=0}。并且{X=3,Y=1}与{X=2,Y=0}互斥,{X=3}与{Y=1},{X=2}与{Y=0}相互独立,由(1)知,P(M)=P({X=3,Y=1}∪{X=2,Y=0})=P({X=3,Y=1})+P({X=2,Y=0})=P(X=3)·P(Y=1)+P(X=2)·P(Y=0)==。
点评:本题主要考查离散型随机变量的分布列与期望,互斥事件与相互独立事件的概率计算公式,也考查特殊分布的期望与方差公式,同时考查同学们应用概率公式解决实际问题的能力。
苏佩斯对科学理论问题的研究始于逻辑经验主义学派向历史主义学派的转型期,这便决定了其问题论证的出发点必然是基于对逻辑经验主义“公认观点”的批判,但他秉持一种多元论的包容性观点,并未对其完全加以否定,而是针对其简单性提出了质问。此外,苏佩斯基于自身多年来对集合论的研究,把较强的数学元素引入讨论中,这使得对理论的阐述在一阶逻辑范围内得以实现。再者,模型作为苏佩斯科学理论研究中的重要基点,“集合论模型”的构建为直接描述科学理论问题提供了更为深入理论本质的探讨。
练习2:一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图1 所示。将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立。
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100 个的天数,求随机变量X的分布列、数学期望E(X)及方差D(X)。
解析:(1)设A1表示事件“日销售量不低于100个”,A2表示事件“日销售量低于50个”,B表示事件“在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个”,因此:
P(A1)=(0.006+0.004+0.002)×50=0.6,P(A2)=0.003×50=0.15,P(B)=0.6×0.6×0.15×2=0.108。
(2)X可能取的值为0,1,2,3,其相应的概率为:
X的分布列如表5:
因为X~B(3,0.6),所以数学期望E(X)=3×0.6=1.8,方差D(X)=3×0.6×(1-0.6)=0.72。
三、利用离散型随机变量的数学期望与方差解决其他问题
例3有一幢楼房共19 层,若选择其中某一层作为会议室,开会时每层去1 人,则会议室设在第几层时,可使每人所走过的路程最短?(每层楼高度相同)
解析:大部分的同学拿到该题首先想到利用等差数列的前n项和公式建立与路程之间的关系,然后求最值,这是一种常规的思路。如果我们换一个角度思考:会议室设在哪一层都是随机的,而设在任一层楼的概率都为。这样,与上面两个问题完全相同,所以我们“希望”会议室所在的楼层即为随机变量的数学期望。
由题意得会议室所在的楼层的分布列如表6:

表6
会议室设在第10层满足题意。
点评:换一种角度,海阔天空,利用离散型随机变量的分布列的数学期望可解决上述问题的最值问题。若把19改为n,则可进一步引申出更为一般的结论:当n为奇数时,会议室应设在层;当n为偶数时,会议室设在层均满足题设要求。
练习3:设n把外形完全相同的钥匙,其中只有1 把能打开大门,用它们去试开门上的锁,若抽取钥匙是相对独立且等可能,每把钥匙用后都不放回,试求开锁次数的数学期望与方差。
解析:求P(ξ=k)时,由题意知前k-1次没有打开,恰好第k次打开,取ξ=1,2,3,发现规律后,再推广到一般。ξ的可能取值为1,2,3,…,n。
故ξ的分布列如表7:
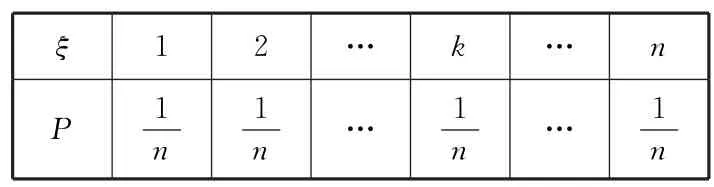
表7
故E(ξ)==。
若按一般方法求方差,显然相当麻烦,我们换作D(X)=E(X2)-(EX)2。
四、利用数学期望和方差制定出正确的方案
例4受轿车在保修期内维修费等因素的影响,每辆轿车产生的利润与该轿车首次出现故障的时间有关,某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2 年,现从该厂已售出的两种品牌轿车中随机抽取50辆,统计数据如表8:
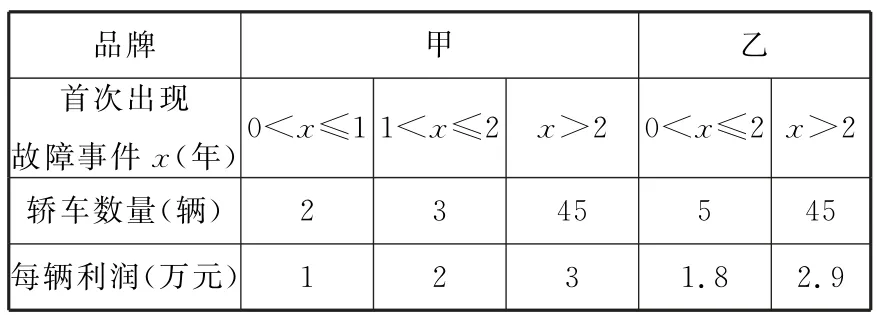
表8
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求首次出现故障发生在保修期内的概率;
(2)若该厂生产的轿车均能售出,设生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列;
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌轿车,若从经济效益的角度考虑,你认为应该产生哪种品牌的轿车,并说明理由。
解析:(1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A,则P(A)=。
(2)依题意得,X1的分布列如表9:

表9
X2的分布列如表10:

表10
(3)由(2)得,E(X1)==2.86(万元);
E(X2)==2.79(万元)。
因为E(X1)>E(X2),所以应生产甲品牌轿车。
点评:利用数学期望来作出决策,在实际问题中有非常重要的比较价值。解决实际应用问题时,关键是正确理解随机变量取每一个值时所表示的具体事件。
