高考中统计与概率试题最新命题趋势

■福建省泉州市第七中学

概率决策思想,突出学科素养导向,着重考查同学们的理性思维能力以及综合运用数学思维方法分析问题、解决问题的能力,试题贴近生活,联系社会实际,反映了数学应用广泛,体现了数学的应用价值,在考试评价中落实立德树人根本任务,对同学们的素质教育有很好的导向和促进作用。纵观近几年高考和省市模拟题,概率好题不胜枚举,它们像一颗颗璀璨的珍珠在数学题海中闪闪发光,下面特精选几例予以分类解析,旨在探究题型考查特点,仅供同学们参考,希望大家能决胜于高考。

一、概率与几何图形牵手，重点考查几何概型

例1(2018 年全国Ⅰ卷)如图1,来自古希腊数学家希波克拉底所研究的几何图形。此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC。△ABC的三边所围成的区域记为Ⅰ,阴影部分记为Ⅱ,其余部分记为Ⅲ。在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则( )。

A.p1=p2B.p1=p3

C.p2=p3D.p1=p2+p3

解析：不妨设△ABC为等腰直角三角形,AB=AC=2,则BC=。所以区域Ⅰ的面积即△ABC的面积,S1=×2×2=2,区域 Ⅱ 的面积S2=π × 12-=2,区域Ⅲ的面积S3==π-2。根据几何概型的概率计算公式,得,所以p1≠p3,p2≠p3,p1≠p2+p3,选A。

也可以令AB=2r1,AC=2r2,BC=2r3,代入对应关系式计算,得答案A。

例2在棱长为2 的正方体ABCDA1B1C1D1中,点O为底面A1B1C1D1的中心,在正方体ABCD-A1B1C1D1内随机取一点P,则点P到点O的距离大于1的概率为_____。

解析：如图2,与点O距离等于1 的点的轨迹是一个半球面,其体积V1=。

事件“点P与点O距离大于1的概率”对应的区域体积为,根据几何概型概率公式得,点P与点O距离大于1 的概率P=。

点评：考查几何概型计算公式：P(A)=。

二、以统计图表为情景材料，通过实验、计算机模拟呈现，考查随机数和估值

例3若采用随机模拟的方法估计某运动员射击击中目标的概率,先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9 表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数：

根据以上数据估计该运动员射击4次至少击中3次的概率为______。

解析：根据数据得该运动员射击4 次至少击中3次的数据分别为7527 9857 8636 6947 4698 8045 9597 7424,共8个,所以该运动员射击4次至少击中3次的概率为=0.4。

例4已知0≤a＜2,0≤b＜4,为了估计在a＞1 的条件下,函数f(x)=x2+2ax+b有2 个相异零点的概率P,用计算机产生了[0,1)内的两组随机数a1,b1各2 400个,并组成了2 400个有序数对(a1,b1),统计这2 400 个有序数对后得到2×2 列联表的部分数据如表1：

表1

则根据表中的数据,计算出概率P的估计值为( )。

解析：依题意可得数据如表2：

表2

因为0≤a＜2,0≤b＜4,函数f(x)=x2+2ax+b有2 个相异零点,所以Δ=4a2-4b＞0⇒a2-b＞0。取变换,因为在a＞1 的条件下,所以满足的数对个数共为1 200 对。又函数f(x)=x2+2ax+b有2 个相异零点,满足Δ=4a2-4b＞0⇒a2-b＞0,即(2a1)2-4b1＞0⇒-b1＞0⇒≥b1,故满足b1＜的数对个数共有650对。则根据表中的数据,计算出概率P的估计值为P=,选C。

点评：本题是源于课本但又被适当改造的一道好题! 试题来源于教材,高于教材,有所创新,难点在于取变换,这体现了数学课本本源思想和学以致用的宗旨。

三、考查回归直线，相关系数，2×2列联表，独立性检验

例5某芯片公司为制定下一年的研发投入计划,需了解年研发资金投入量x(单位：亿元)对年销售额y(单位：亿元)的影响。该公司对历史数据进行对比分析,建立了两个函数模型：①y=α+βx2,②y=eλx+t,其中α,β,λ,t均为常数,e为自然对数的底数。现该公司收集了近12年的年研发资金投入量x1和年销售额y1的数据,i=1,2,…,12,并对这些数据作了初步处理,得到散点图(图3)及一些统计量的值。

令ui=,vi=lnyi(i=1,2,…,12),经计算得如下数据(表3、表4)：

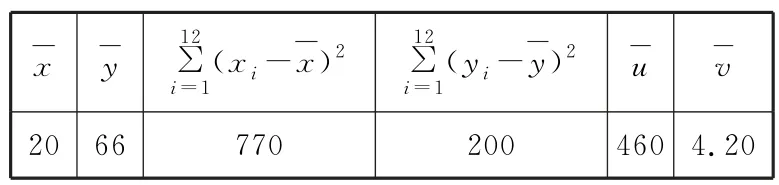
表3

表4

(1)设{ui}和{yi}的相关系数为r1,{xi}和{vi}的相关系数为r2,请从相关系数的角度,选择一个拟合程度更好的模型。

(2)(i)根据(1)的选择及表中数据,建立y关于x的回归方程(系数精确到0.01);

(ii)若下一年销售额y需达到90亿元,预测下一年的研发资金投入量x是多少亿元。

附：①相关系数r=,回归直线=a+bx中斜率和截距的最小二乘估计公式分别为：

解析：(1)r1====0.86,r2==≈0.91,则|r1|＜|r2|,因此从相关系数的角度来说,模型y=eλx+t的拟合程度更好。

(2)(i)先建立v关于x的线性回归方程。由y=eλx+t,得lny=t+λx,即v=t+λx。

由于λ=≈0.018,t==4.20-0.018×20=3.84,所以v关于x的线性回归方程为v=0.02x+3.84,即lny=0.02x+3.84,y=e0.02x+3.84。

(ii)下一年销售额y需达到90亿元,即y=90,代入y=e0.02x+3.84得,90=e0.02x+3.84。又e4.4998≈90,故4.499 8≈0.02x+3.84。

解得x≈=32.99。

所以预测下一年的研发资金投入量约是32.99亿元。

点评：求回归方程要求线性相关,如不是,应通过换元构造线性相关。

四、利用正态分布(μ,σ)原则进行数据分析，注意运算的技巧

例6(2017 年新课标Ⅰ卷)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位：cm)。根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2)。

(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望。

(2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查。(i)试说明上述监控生产过程方法的合理性;(ii)下表是检验员在一天内抽取的16个零件的尺寸：

表5

附：若随机变量Z服从正态分布N(μ,σ2),则P(μ-3σ＜Z＜μ+3σ)=0.997 4,0.997 416≈0.959 2,≈0.09。

解析：(1)抽取的一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率为0.997 4,从而零件的尺寸在(μ-3σ,μ+3σ)之外的概率为0.002 6,故X～B(16,0.002 6)。因此P(X≥1)=1-P(X=0)=1-0.997 416=0.040 8。X的数学期望E(X)=16×0.002 6=0.041 6。

(2)(i)如果生产状态正常,一个零件尺寸在(μ-3σ,μ+3σ)之外的概率只有0.002 6,一天内抽取的16个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有0.040 8,发生的概率很小。因此,一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的。

点评：运算求解能力主要是指会根据法则、公式进行正确运算和数据处理,能根据问题的条件寻找与设计合理、简捷的运算途径,能根据要求对数据进行估计和近似计算。从高考改卷反馈和运算方面看,有些同学不知从s=≈0.212中解出;不会由=9.97和s≈0.212计算出区间(-3σ,+3σ)的端点值9.334,10.606;计算=时,不懂得反向处理数据或各项统一分离10后转化为;计算=时,不懂得先转化为,再利用=9.97简化运算;计算s2=[0.072+0.12+0.062+0.062+0.012+0.12+0.042+0.022+0.242+0.112+0.112+02+0.022+0.032+0.072]=0.008 13≈0.008,不懂各项统一提取0.012的技巧;计算s2=[16×0.2122+16×9.972-9.222-15×10.022]时,不懂得在保证精确度要求的前提下进行近似处理以简化运算。

五、采用统计知识对比分析，为相应决策提供依据

例7(2018 年全国卷Ⅰ卷)某工厂的某种产品成箱包装,每箱200 件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格产品,则需要换为合格产品。检验时,先从这箱产品中任取20 件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为p(0＜p＜1),且各件产品是否为不合格品相互独立。

(1)记20件产品中恰有2件不合格产品的概率为f(p),求f(p)取最大值时p的值p0。

(2)现对一箱产品检验了20 件,结果恰有2件不合格品,以(1)中确定的p0作为p的值。已知每件产品的检验费用为2 元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用。

(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求E(X);(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?

解析：(1)20 件产品中恰有2 件不合格产品的概率为。

因此,f′(p)=[2p(1-p)18-18p2(1-p)17]=(1-p)17(1-10p)。

令f′(p)=0,得p=0.1。当p∈(0,0.1)时,f′(p)＞0;当p∈(0.1,1)时,f′(p)＜0。

所以f(p)取最大值时p=p0=0.1。

(2)由(1)知,p=0.1。(i)令Y表示余下的180件产品中的不合格品件数,依题意知Y～B(180,0.1),X=20×2+25Y,即X=40+25Y。所以E(X)=E(40+25Y)=40+25E(Y)=490。(ii)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元。由于E(X)＞400,故应该对余下的产品作检验。

点评：统计与概率问题与实际生活联系十分密切,来源于实际生活,又服务于实际生活,因此在高考试卷中常扮演着考查同学们应用数学知识解决实际问题能力的角色,可依据统计学中的方法对数据进行分析,作出合理的决策。

六、统计与数列交汇，考查小概率事件，体现了统计与概率应用的广泛性

例8(2019年高考新课标Ⅰ卷)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验。试验方案如下：每一轮选取两只白鼠对药效进行对比试验。对于两只白鼠,随机选一只施以甲药,另一只施以乙药。一轮的治疗结果得出后,再安排下一轮试验。当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效。为了方便描述问题,约定：对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1 分,甲药得-1分;若都治愈或都未治愈则两种药均得0分。甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X。

(1)求X的分布列。

(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1)。假设α=0.5,β=0.8。

(i)证明：{pi+1-pi}(i=0,1,2,…,7)为等比数列;(ii)求p4,并根据p4的值解释这种试验方案的合理性。

解析：(1)X的所有可能取值为-1,0,1,P(X=-1)=(1-α)β,P(X=0)=αβ+(1-α)(1-β),P(X=1)=α(1-β)。

所以X的分布列如表6：

表6

(2)(i)由(1)得a=0.4,b=0.5,c=0.1。

因此pi=0.4pi-1+0.5pi+0.1pi+1,故0.1(pi+1-pi)=0.4(pi-pi-1),即pi+1-pi=4(pi-pi-1)。

又因为p1-p0=p1≠0,所以{pi+1-pi}(i=0,1,2,…,7)是公比为4,首项为p1的等比数列。

(ii)由(i)可得：

p8=p8-p7+p7-p6+…+p1-p0+p0=(p8-p7)+(p7-p6)+…+(p1-p0)=。

由于p8=1,故p1=。

所以p4=(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)+p0=。

p4表示最终认为甲药更有效的概率,由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为p4=≈0.003 9,此时得出错误结论的概率非常小,说明这种试验方案合理。

点评：当创新性问题的情境很复杂时,静下心来读懂题意是第一要务,在读懂题意的前提下抽象概括出数学模型,以便顺利解题。

统计与概率进一步强化应用意识的考查,已成高考命题改革的必然趋势。试题文字阅读量的逐年增加,或成高考试卷的发展趋势,因此,同学们在学习时关注生活背景、社会现实、经济建设、科技发展等各个方面,注意培养大家善于从普通语言中捕捉信息、将普通语言转化为数学语言的能力,加强平时的阅读训练和指导,应该呈现读题提取关键信息、分析题形成解题思路、解题规范表达、反思积淀解题经验的“四部曲”完整过程,才能充分发挥解题学习的效益。