基于SOA优化PID控制参数的智能灌溉控制策略研究

许景辉 王 雷 谭小强 王一琛 赵钟声 邵明烨

(1.西北农林科技大学旱区农业水土工程教育部重点实验室， 陕西杨凌 712100；2.西北农林科技大学水利与建筑工程学院， 陕西杨凌 712100；3.西北农林科技大学机械与电子工程学院， 陕西杨凌 712100)

0 引言

中国是农业大国，农业灌溉用水占据水资源的绝大部分，但传统的灌溉方式造成了水资源的大量浪费。智能灌溉系统通过水泵自动供水设施将作物所需的水分按需供给，促进作物根系生长[1-3]。水泵供水过程中，给水量在最优控制范围内有利于作物根系的发育及土壤中矿物质的吸收[4]。因此，按照作物需水进行水泵供水精确控制是实现智能灌溉的关键。

水泵控制系统存在非线性、时变性和滞后性等问题，这将影响智能灌溉系统的整体运行效率。目前，国内外主要采用PID控制和模糊控制策略来实现作物智能灌溉，通过调整相应的参数来实现相关设备控制器的精度，从而取得较好的控制效果[5-8]。PID控制是灌溉控制系统普遍采用的控制方法[9]，其控制算法简单、参数调整方便、鲁棒性好、可靠性高，适用于各种工况[10-11]，但PID控制存在过渡过程时间和超调量之间的矛盾。PID控制的效果主要取决于参数的整定[12-13]，不同的控制对象及控制参数对控制系统产生的影响不同。李俊勇等[14]提出采用改进的遗传算法和模糊控制技术相结合，通过对PID参数整定的优化，使控制器具有良好的控制效果。江金龙等[15]提出一种基于遗传算法和直接搜索策略的PID参数整定方法，研究表明，该方法提高了搜索精度和收敛精度。李开霞等[10]提出一种通过实时整定PID参数的自适应PID控制策略，该策略可以应用于多功能除湿机的温控，具有较好的稳定性。但PID控制策略需要凭借经验和反复调试来整定PID参数，工作费时、费力，并且将传统的PID控制用于现代智能灌溉系统中的水泵控制，其控制精度达不到要求。因此，需要根据灌溉水机电系统的传递函数自适应PID参数，以达到目前智能灌溉系统中精准控制、精准灌溉的要求。

本文以智能灌溉系统中水泵机电系统为被控对象，选取特定工作条件下的水泵供水传递函数，基于人群搜索优化算法(Seeker optimization algorithm，SOA)实现灌溉控制系统的PID控制参数优化，分析其响应时间及稳定状态。将粒子群算法(Particle swarm optimization，PSO)和遗传算法(Genetic algorithm，GA)与SOA进行比较，分析3种优化策略在水泵供水控制中的效果，以实现精度高、稳定性好的水泵供水控制，为实现精准的智能灌溉系统提供技术支持。

1 基于SOA优化的PID控制系统设计

1.1 PID控制

在模拟控制系统中，PID控制器是一种线性控制器[16-17]，系统由控制器和被控对象组成，其模拟控制系统框图如图1所示。

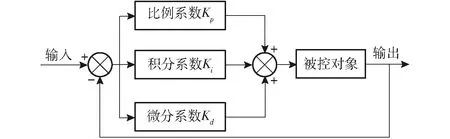
图1 PID控制系统框图Fig.1 PID control system block diagram

PID控制器由比例环节(Proportional)、积分环节(Integral)和微分环节(Differential)组成[18]，PID的控制规律表示为

(1)

将式(1)写成传递函数的形式

(2)

式中Ti——积分时间常数

Td——微分时间常数

e(t)——系统误差

u(t)——控制输出

G(s)——系统传递函数

E(s)——输出函数

U(s)——输入函数

s——复数变量

对于PID控制器而言，当采样周期比较短时，可采用PID的离散化处理，即可通过离散化将连续系统直接转换为差分方程。为此，用一阶差分式代替微商，用求和代替积分，用矩形积分代替连续积分的近似值，即可求出PID控制器的离散方程。公式为

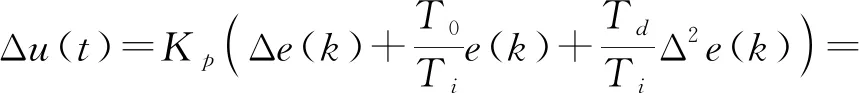
(3)

式中T0——采样周期

e(k)——k时刻控制偏差

虽然传统PID控制工作稳定且控制结构简单，但对于一个具有非线性、时变性和滞后性的智能灌溉系统，其Kp、Ki、Kd3个参数调整复杂，为了满足全局最优调控和缩短过渡的时长，需要通过PID优化算法以提高其控制效果[19-21]。

1.2 SOA优化PID控制

1.2.1SOA算法

人群搜索优化算法(SOA)是进化算法研究领域的一种新型群体智能算法，该算法立足传统的直接搜索算法，将搜索队伍作为种群，以各搜索者所处位置作为候选解，通过模仿人类在进行搜索行为时对位置和方向等的推理判断完成问题的最优求解，采用SOA优化的PID参数整定，具有收敛快、鲁棒性好和稳定性高等特点[22]。

SOA算法具体描述为[23]：假定在维度为D的空间中有S个搜寻个体，则个体i所处的位置为

Xi=[xi1xi2…xiD]T

(4)

由于PID控制器由3个主要的控制参数Kp、Ki、Kd决定，则设定SOA优化算法的个体维度为3，能够实现对PID控制器参数进行优化整定。适应度函数是搜寻者优化算法与控制系统结合的纽带，指导算法按控制目标要求不断进化。为了获取满意的过程动态特性，采用误差绝对值的时间积分性能指标作为最小目标函数。同时，为了防止控制能量过大，引入控制输入平方项，即目标函数为

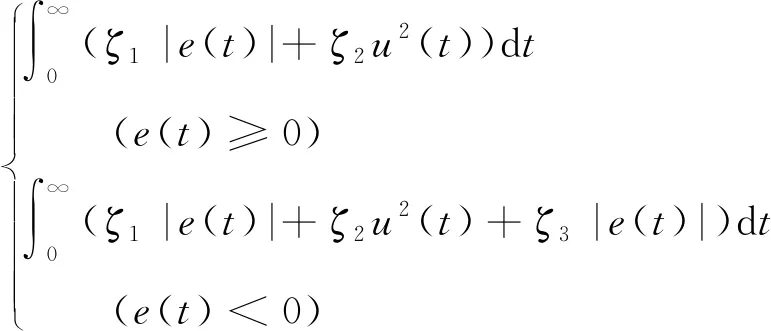
(5)

式中ζ1、ζ2、ζ3——权值系数，ζ3≫ζ1

为了避免超调，采用了惩罚控制，通过对比试验，式(5)权值系数ζ1、ζ2、ζ3一般取0.999、0.001、100可实现较好控制效果。

SOA的不确定推理行为是利用模糊系统的逼近能力，模拟人的智能搜索行为，用以建立感知(目标函数值)和行为(步长)之间的联系，搜索步长表示为

(6)

式中αij——j维搜索空间的搜索步长

δij——高斯隶属函数参数

uij——j维搜索空间目标函数值i的隶属度

通过对人的利己行为、利他行为和预动行为的分析和建模，确定搜索方向为

di(t)=sign(ωdi,pro+φ1di,ego+φ2di,alt)

(7)

式中di,pro——搜寻个体预动方向

di,ego——搜寻个体利己方向

di,alt——搜寻个体利他方向

ω——惯性权值，随进化代数的增加从0.9线性递减至0.1

φ1、φ2——0～1之间常数

1.2.2PID控制器的SOA算法优化设计

基于SOA算法优化的PID控制流程如下：①初始化每个搜索者的个体位置，系统随机产生初始位置矩阵。②计算搜索个体的适应度。③对当前每个搜索者个体位置与其历史最佳位置进行比较，选择和保留最优个体位置进行更新。④对种群历史最优位置与当前个体最优位置进行比较，若当前搜索个体更好则对种群历史最优位置进行更新替换。⑤如果未达到结束条件，返回步骤②，否则结束循环。

依据上述算法原理设计基于SOA优化PID控制的水泵供水控制系统，如图2所示。

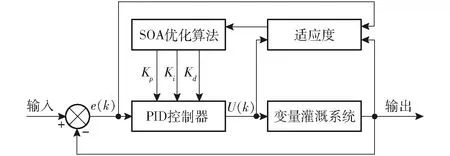
图2 基于SOA优化PID控制的智能灌溉控制系统原理框图Fig.2 Block diagram of intelligent irrigation control system based on SOA optimized PID control

2 被控对象模型

智能灌溉系统中水泵供水系统可认为是一种压力不断变化的稳压供水系统，稳压供水系统是通过调节变频器改变水泵的供水量，从而达到水压稳定的目的[24]。国内也有提出变压供水，其机理是从恒压供水演变而来，分为压力上升阶段和恒压阶段，压力上升阶段是一阶惯性环节，恒压阶段为纯滞后环节，则供水系统模型可表示[25-26]为

(8)

式中T1——供水系统的惯性时间常数，s

k1——供水系统的增益

τ——供水系统的时滞常数，s

np——传递函数输入，即供水系统中离心泵的转速

p0——传递函数输出，即供水系统的出口压力

G1——供水系统传递函数

变频器和水泵电动机可近似为等效时间常数T2的一阶惯性环节，可表示为

(9)

式中T2——调速系统的惯性时间常数，s

k2——调速系统的增益

fc——传递函数输入，即供水系统中变频器的输入频率

nm——传递函数输出，即供水系统中电动机的转速

G2——调速系统传递函数

系统中其他控制及检测环节与供水系统的时间常数相比可以忽略，可以看作一个比例环节

G3=k3

(10)

式中G3——其他系统传递函数

k3——其他系统增益

设定智能灌溉系统中供水系统采用离心泵供水，则该系统中电机的转速等于离心泵的转速，从而整个供水系统的模型可表示为上述3个环节的串联模型，可表示[25]为

(11)

其中

k=k1k2k3

式中k——系统的总增益

G——系统传递函数

T1主要由用户的数量决定，T2主要由变频器加速时间常数和电动机的自身特性决定，τ由管网系统的最不利点与用户的距离和系统中水的平均流速决定。

蒙蕊蕊等[27]通过模型辨识对离心泵供水做了大量实验，辨识出不同工况下离心泵的传递函数。本次仿真传递函数选用其研究中初始频率为30 Hz、目标频率为40 Hz且球阀打开数为1工况下的传递函数。在一定范围降频、参数变化小等工况中可以认为是一阶惯性加时滞的模型，但当系统处于升频或参数变化较大、较快的过程中，系统模型变为二阶惯性加时滞模型，模型结构较复杂。本文选择系统处于升频状态，因此系统模型为二阶惯性加时滞，模型传递函数为

(12)

3 仿真测试与结果分析

为了验证SOA优化PID控制算法的优越性，采用PSO优化算法和GA优化算法进行Matlab仿真对比。分别编写基于SOA、PSO和GA优化下的PID控制算法代码，对以上选取的水泵控制系统进行仿真实验，设该系统种群规模为30，最大迭代次数为100次，最大隶属度为0.950 0，最小隶属度为0.011 1，权重最大值为0.9，权重最小值为0.1，维数为3，得PSO、GA、SOA 优化适应度函数控制曲线、系统阶跃响应输出曲线和系统阶跃响应输出误差曲线分别如图3～5所示。

图3 适应度函数控制曲线Fig.3 Fitness function control curves

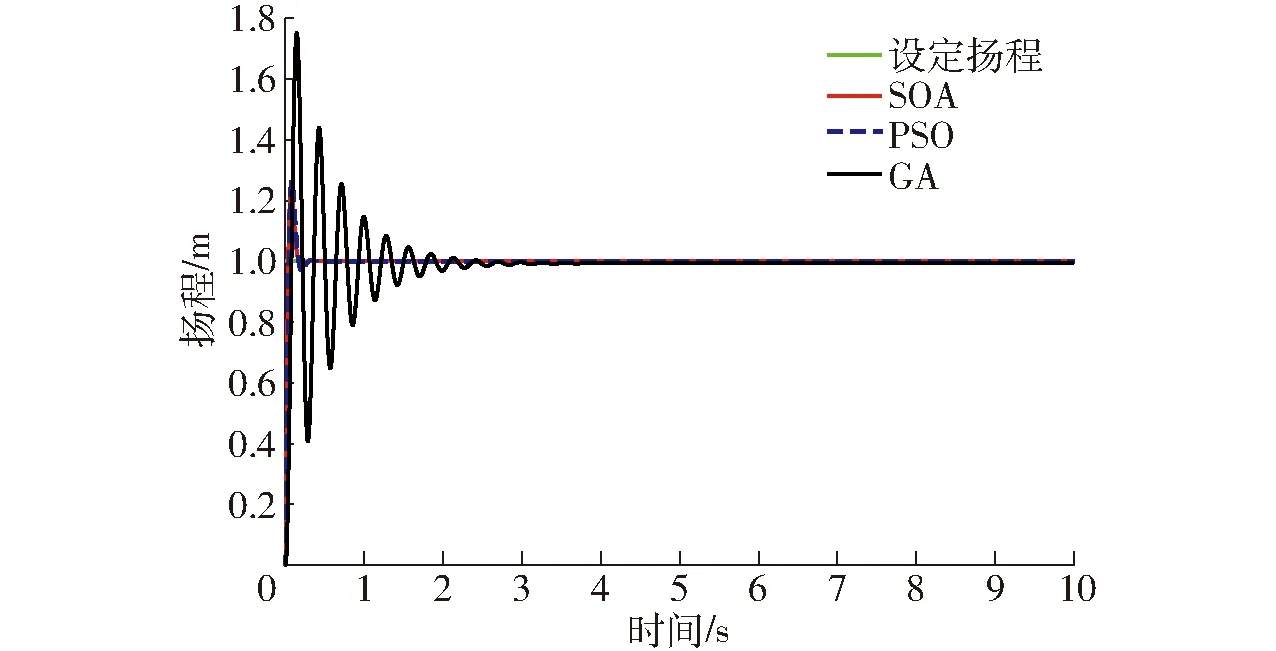
图4 SOA、PSO、GA系统阶跃响应输出曲线Fig.4 Step response output curves of SOA, PSO and GA systems

图5 SOA、PSO、GA系统阶跃响应输出误差曲线Fig.5 Step response output error curves of SOA, PSO and GA systems

由图3可知，在3种优化算法寻找适应度函数的最优适应度时，PSO优化算法寻找最优适应度最快，仅需要2次迭代就找出了该适应度函数的最优适应度，SOA优化算法次之，在第8次迭代完成后找到该适应度函数的最优适应度，而GA优化算法最差，在第74次迭代后找出了该适应度函数的最优适应度。由此可见，SOA和PSO优化算法在确定适应度函数的最优适应度速度较快且稳定性较好，而GA优化算法速度慢且稳定性较差。由图4可知，GA优化算法到达平稳所需的时间为3.50 s，最大超调量为0.75 m，而SOA和PSO优化算法达到平稳所需时间均小于0.50 s、最大超调量均小于1.3 m，且上升时间均小于GA优化算法的上升时间，因此，SOA和PSO优化算法相对收敛快、控制精度高，而GA优化算法上升用时及收敛用时较长，超调量较大。由图4可知，SOA优化算法与PSO优化算法的PID控制系统相比，上升时间减少了0.01 s，超调量降低了0.06 m。表明SOA优化的PID智能灌溉控制系统具有更好的控制效果和鲁棒性。由图5可知，GA优化算法误差最大，最大误差为0.72 m，而SOA和PSO优化算法的最大误差均不大于0.27 m，误差相对较小。SAO优化算法的最大误差为0.22 m，而PSO优化算法的最大误差为0.27 m。因此，SAO优化算法误差更小。综上所述，智能灌溉系统中的水泵供水控制系统基于SOA优化的PID控制效果最优，可应用于智能灌溉系统控制。

4 基于SPWM的智能灌溉机电控制系统仿真模型验证

4.1 SPWM控制原理

SPWM控制技术旨在控制变频器的输出电压来满足交流调速系统的需要。其基本控制思想是等效原则，即用一定数量宽度不等(半个周期内，两侧波形窄，中间波形宽)幅值相等的脉冲矩形波来等效正弦波，如图6所示。SPWM波形与正弦波等效的具体内容是将正弦波曲线的一个周期等分成若干份，每一段小周期内的正弦波曲线所围面积，用一系列高度相等，宽度中心与每一小段周期的1/2处相重合的矩形脉冲波的面积来等效，就可以得到需要等效的一系列SPWM脉冲波。

图6 SPWM脉冲波形Fig.6 SPWM pulse waveform

4.2 灌溉控制系统模型建立

运用Matlab中Step模块设置转速给定值，并与实际转速进行比较得到转速偏差。利用异步电动机转速与频率的关系将转速偏差转换成频率偏差，经PID控制器得到系统控制量。由于实际情况中频率控制难以瞬时变化，采用Rate Limiter模块实现控制频率上升和下降，为了在0.25 s内完成0～50 Hz的加速，Rate Limiter的参数可分别为200和-200。恒压频比控制V/F曲线则由1-D Lookup Table模块来实现。上述模块设置参数后与SPWM控制器模型连接就构成了智能灌溉控制系统模型。将主电路、水泵模型、灌溉控制系统连接得到图7所示变量灌溉控制系统仿真模型。

图7 基于SPWM的智能灌溉控制系统仿真模型Fig.7 Simulation model of intelligent irrigation control system based on SPWM

设置转速给定值为1 400 r/min(0～1 s)和1 200 r/min(1～2 s)，相当于水泵给定扬程为23.25 m(0～1 s)和17.08 m(1～2 s)。系统PID参数经传统人工调整可以得到图8所示的水泵出口压力变化曲线。系统PID参数经SOA优化调整则可得到图9所示曲线。

图8 传统人工调节PID参数的水泵出口扬程跟踪曲线Fig.8 Pump outlet head tracking curves of traditional manual adjustment PID parameters

从图8、9可以看出，灌溉系统的PID控制策略通过SOA优化后，其参数较人工调整具有很好的控制效果。在变量灌溉系统压力波动较大时，其控制压力的超调量很小，利于变量灌溉机电系统的稳定运行。

5 结论

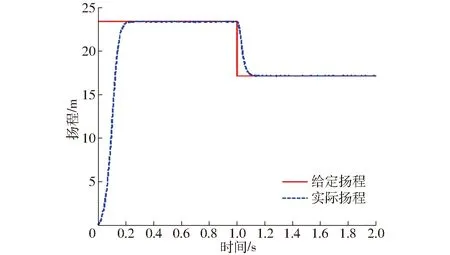
图9 SOA优化PID参数的水泵出口扬程跟踪曲线Fig.9 Pump outlet curves of SOA optimized PID parameters

(1)基于SOA算法优化的PID控制在水泵供水控制中调节时间短、超调量小，稳态特性与动态响应特性均最优，通过SOA算法可以实现智能灌溉控制系统中的最优控制策略。

(2)SOA算法在优化过程中，适应度和粒子群数量的调整可有效提高PID数值优化效果，能在一定程度上解决传统PID控制在智能灌溉系统中水泵供水控制系统的非线性、时变性和滞后性问题。

(3)仿真验证结果表明，基于SOA算法优化的PID控制稳定性及动态性能较好，可以很好地满足水泵供水控制系统的自动控制要求，可应用于实际智能灌溉系统。