基于双峰分布的风胁迫雾滴沉积分布模型研究

梁 昭 范国强,2 王光明,3 丁 皓 张晓辉,2

(1.山东农业大学机械与电子工程学院， 泰安 271018； 2.山东农业大学山东省农业装备智能化工程实验室， 泰安 271018；3.山东农业大学山东省园艺机械与装备重点实验室， 泰安 271018)

0 引言

雾滴飘移是产生农药污染的主要原因，在施药过程中，喷头喷雾的药液在空间中形成雾滴粒子群，粒子群受到空间气流场的胁迫作用而发生偏移，沉积在非靶标区域[1-3]。随着人们对生态环境保护和食品安全重视程度的提高，以及农业生产中农药使用量的增加和使用范围的扩大，农药施药过程中因风胁迫产生的雾滴飘移现象受到人们高度关注[4-6]。雾滴飘移会使药液沉积在非目标区域，对周边环境产生影响，且造成目标区域施药不均匀。

雾滴在空中受气流胁迫而改变沉降的位置，其受到多种因素的影响，主要包括喷头喷出雾滴大小[7-10]、喷雾压力[11]、药液本身的化学性质[12]、空间气流场大小和方向[13]、喷雾高度和角度[14]、施药设备搭载平台的移动速度[15]和采样距离[16]等。多种因素影响了雾滴粒子群沉降速度，改变了雾滴的空间运动轨迹，因此造成了雾滴飘移沉积分布的改变[17-19]。张京等[20]研究了扇形喷雾雾化过程中雾滴运动的特性，确定了雾滴在喷雾扇面内的速度分布，发现扇形边缘的雾滴小，速度低，更容易飘失。宋坚利等[21]通过PDPA对扇形喷头雾化的雾滴进行了分析，结果表明，在距离喷头300～500 mm喷雾扇面的中心位置处的雾滴，以及扇面的末端和两侧的雾滴易发生飘移。刘雪美等[22]采用三维流场的多相流系统进行仿真，发现辅助气流可以有效减少飘移量，当喷雾压力降低时，风幕的防飘移效果更好。苑进等[23]通过模糊决策支持系统对作物茂密程度和喷嘴与冠层间垂直距离进行控制参数修正，减少了雾滴飘失率。杨洲等[24]研究了不同侧风和静电充电电压对荷电雾滴飘移的影响。张慧春等[25-26]通过风洞试验建立了雾滴飘移的回归模型，并研究了雾滴的脱靶飘移现象，确定了不同体积中径、喷雾角、雾滴速度、流量、喷头高度、风速、植物类型、生长阶段等因素对农药雾化后飘移的影响。李超等[27]研究了辅助气流对雾滴中心飘移距离的影响。

本文通过在封闭试验场内生成不同的恒定胁迫气流场，在不同喷雾高度和喷雾压力条件下对雾滴飘移进行研究，根据飘移的沉积质量分布建立描述其分布特性的数学模型，探究不同强度横风作用和喷雾高度、压力对雾滴飘移沉积质量的影响，探寻不同施药条件对沉积模型参数的影响规律。

1 试验材料与方法

1.1 试验设备

图1 封闭式喷头喷雾沉积量检测试验台Fig.1 Test bed for closed spray deposition measurement1.槽式导流板 2.收集器 3.扇形喷嘴 4.温度传感器 5.三杯风速传感器 6.加热器 7.封闭仓支架 8.轴流风机 9.高度调节架 10.水泵

试验采用封闭式喷头喷雾沉积量检测系统。为了使沉积区域及其周边的微气象条件保持稳定，本文构建室内风场试验台，以减少环境温度、湿度、光照等对雾滴飘移的影响。该系统主要包括封闭仓、绝热层、水泵、高度调节架、控制器、温度传感器(LGHTM-01A型)、风速传感器(HS-FS01型)、扇形喷嘴(HYPRO-01型)、调速轴流风机(SF5-4型)、槽式导流板、收集器、加热器(HN2188PT型)等。其结构示意图如图1a所示，实物图如图1b所示。

封闭仓被闭孔式橡塑海绵包覆，内部贴装有双面铝箔气泡膜，以维持封闭仓内部环境的稳定。试验舱顶部有照明系统和加热器材(功率：1.8 kW)，使其内部试验空间维持稳定的温度(试验温度20℃)，当3个与喷头同高度的温度传感器达到20℃时，加热器停止工作。槽式导流板的制作材料为亚克力塑料板，单个导流槽槽宽为2 cm，可以更加细化不同位置区间内的雾滴沉积量。导流槽一侧封闭，另一侧通过小导管将沉积药液导入试管内。扇形喷嘴(HYPRO-01型)喷雾角为110°，其参数如表1所示。

表1 HYPRO-01型扇型喷嘴工作参数Tab.1 Parameters of HYPRO-01 fan nozzle

1.2 试验设计

为研究不同强度胁迫气流(横风风速)、喷雾压力和喷雾高度对雾滴沉积分布情况的影响，设计了三因素三水平试验。在大田中进行施药作业时，要求风力等级不能高于3级(v≤3.3 m/s)；喷杆喷雾机作业高度一般为35～75 cm，最佳高度为50 cm，而在有风情况下作业，降低高度可以减少雾滴飘移[14]；喷杆喷雾机喷雾压力为0.2～0.6 MPa，增大压力可以增加雾滴速度，减少雾滴打到靶目标的时间来减少飘移[11]，因此设计试验因素水平如表2所示。

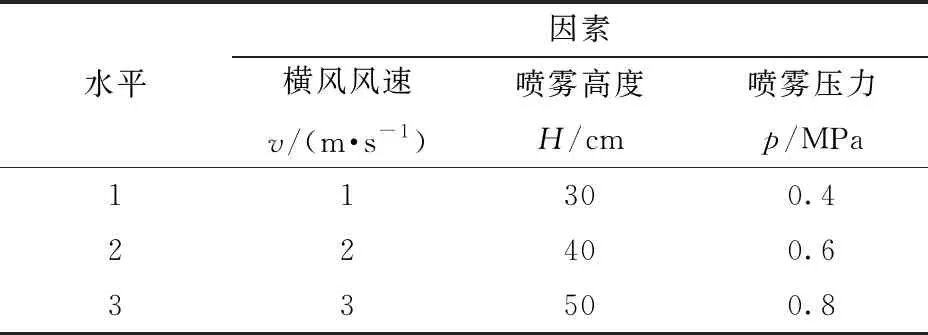
表2 试验因素水平Tab.2 Experimental factor level

试验布置如图2所示，喷头竖直向下，距离槽式导流板的高度为H。喷嘴扇面与导流槽平行，与来风方向垂直。经多次前期试验，确定雾滴沉积范围不超过喷头水平方向10 cm，故设置喷头水平方向距导流板来风侧边10 cm。为方便雾滴收集，导流板与水平面倾角为5°，收集边较低，每个导流槽下方放一个试管对液体进行收集。试验开始关闭封闭仓，打开风机、加热器和照射灯光，通过三杯风速传感器对喷头位置的风速进行标定。待其内部空间温度稳定在20℃后，调整高度调节架，打开水泵开始喷雾并调整压力到规定值，此时药液不流入试管。当导流板收集侧的小管口有均匀的液滴滴下后，开始计时并移动收集器到收集槽导流管下方的收集位置，使药液流入收集试管中。为了建立沉积分布模型，需要长时间收集各个导流槽内的沉积量，使因胁迫气流产生的飘移尾部沉积效果更加明显，通过多次试验，确定在经过240 s喷射后，有明显药液沉积试管中，药液沉积量均大于1 mL，此时收集药液量低于1 mL的试管，其管内的药液量随时间的增加，增加量不明显，故以240 s为沉积药液的收集时间。经过240 s喷射后，统计每个导流槽内收集的液滴沉积量。每组试验重复3次，每个导流槽的沉积量取3次试验值的平均量。

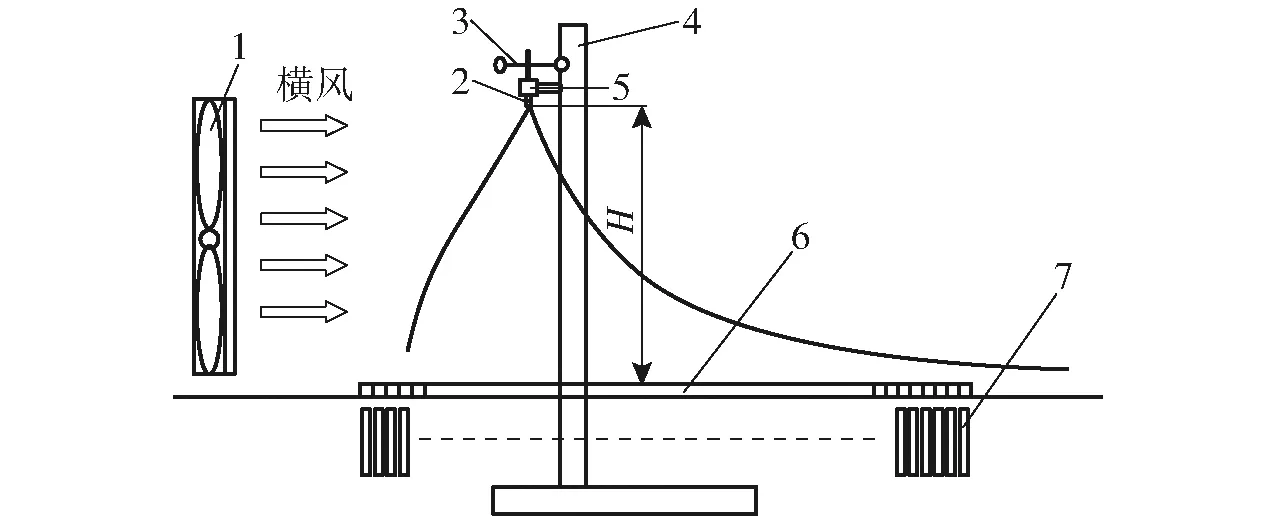
图2 雾滴飘移试验布置示意图Fig.2 Layout of spray drift set-up1.风机 2.喷头 3.三杯风速传感器 4.高度调节架 5.支架 6.槽式导流板 7.收集架

2 模型拟合

2.1 正态分布模型拟合

在喷雾高度为40 cm、喷雾压力0.4 MPa、无横风胁迫的情况下，沉积分布如图3所示。

图3 无横风下雾滴沉积分布情况Fig.3 Distribution of fog droplet deposition without cross wind

由图3可知，在无横风的情况下，雾滴在扇面垂直方向上的沉积分布呈现以喷嘴为中心，左右对称的正态分布。正态分布概率密度函数可表示为

(1)

式中x——沉积距离

μ——均值中位数

σ——标准差

根据沉积量，通过高斯函数进行拟合，求解沉积量在高斯函数模型下的各个参数。高斯函数定义为

(2)

(3)

b=μ

(4)

c=σ

(5)

式中a、b、c——拟合参数

w——收集槽宽度与单位宽度的比

k——沉积量参数

由式(2)～(5)可得高斯函数可用正态分布概率密度函数表示为

(6)

式(6)除以宽度比值w，即得到雾滴飘移沉积分布模型为

(7)

在模型中，均值中位数μ表示沉积量分布集中的位置，称为位置参数；标准差σ表示以μ为中心的沉积量的分布范围。

对风向上某一距离区间内所有雾滴的沉积量和，称为该区间的雾滴沉积量。由式(6)进行积分变换，可得雾滴沉积量分布表达式为

(8)

单位时间内雾滴沉量为

(9)

式(8)表示在距离p到距离q的区间时间t内的雾滴飘移沉积量，其中距离p到距离q的区间为沉积区域。根据正态分布概率密度函数性质，则雾滴主要沉积区域为(μ-3σ,μ+3σ)，此区域沉积量为总量的99%。在区域(μ-2σ,μ+2σ)的雾滴沉积量为总量的95%。

当喷雾高度40 cm、喷雾压力0.4 MPa、喷头水平位置为10 cm时，不同风速下的沉积分布情况如图4所示。此状态下呈现正偏态分布，雾滴沉积质量的平均数大于中位数，峰值左偏，左右出现非对称状态。

图4 有横风下雾滴飘移沉积量Fig.4 Droplet drift deposition under transverse wind

由式(2)可知，分别对无横风胁迫和不同风速胁迫的雾滴沉积分布进行拟合，并转换为正态概率分布形式。在无横风胁迫的情况下，其拟合效果较好。不同风速下的决定系数如表3所示。

表3 决定系数Tab.3 Determination coefficient

图5 沉积量拟合效果Fig.5 Deposition fitting effects

拟合曲线如图5所示。随着横风速的增大，沉积量的主要分布区域发生了少量偏移和扩大，但其区域内的沉积量远大于其他区域，体现了雾滴飘移分布中的沉积量集中性。沉积分布后方区域出现明显的“尾巴”，质量分布不再呈现对称分布，即为飘移分布的沉积特性，具有重尾性[28]。其重尾性的数学表达式为

(10)

式中λ——任意大于0的常数

试验中槽式导流板没有收集全部的尾部沉积量，但已反映了沉积质量的变化趋势，设其尾部区域的沉积量分布符合正态分布，则可根据已有数据估计其参数[29-30]。

2.2 双峰分布模型拟合

随着胁迫横风风速的增大，通过正态分布概率密度函数模型拟合的沉积分布方程的决定系数减小，说明方程符合度降低。为此引入多峰正态分布式

(11)

式(11)是多个独立的正态分布概率函数乘以每个分布对应的沉积量参数的和。由式(11)和式(3)～(5)可使多峰正态分布式变换为n项高斯函数的和，即

(12)

用Matlab中Curve Fitting Tool，采用式(12)对试验中雾滴沉积量进行拟合，当n取不同值时，不同横风风速下，其拟合方程的决定系数如表4所示。

表4 不同横风风速的模型拟合决定系数Tab.4 Model fitting determinants at different transverse wind speeds

由表4可知，当n≥2时，拟合函数的决定系数R2≥0.95，说明拟合效果较好，所以对有横风胁迫的雾滴沉积分布模型采用2个独立的正态分布概率函数乘以对应的质量参数和的形式，即双峰分布模型

(13)

则雾滴在任意区域(p,q)中的沉积量为对双峰分布模型的积分，即

(14)

2.3 双峰分布沉积模型性质

双峰分布模型是2个独立正态分布模型的和，存在2个峰值。2个独立正态分布模型互不干涉，有独立的特征值参数，其表达式分别为式(13)中的第1项和第2项，即

(15)

(16)

式(15)为第1峰值的分布模型，主要体现雾滴沉积分布的集中性。式(16)为第2峰值的分布模型，主要体现雾滴沉积分布的重尾性。由正态分布概率密度函数的性质，可得双峰分布沉积模型的性质。

第n峰分布的沉积质量为

(17)

沉积量中心飘移的距离为

Dn=μn-d

(18)

式中d——喷嘴与来风侧边沿的水平距离

沉积最大飘移沉积距离为

L=μ2+3σ2-d

(19)

尾部区域质量为

(20)

在飘移距离L内，沉积量超过总沉积质量99%，为该分布的主要沉积区域。不同峰值不同区域内沉积质量与该峰值总质量的比值为该区域的质量占比，其计算式为

(21)

不同沉积区域的质量占比见表5。当沉积区域为(μn±3σn)时，质量占比超过99%，则该区域为此峰值的沉积区域，区域示意图如图6所示。

表5 质量占比Tab.5 Mass proportion

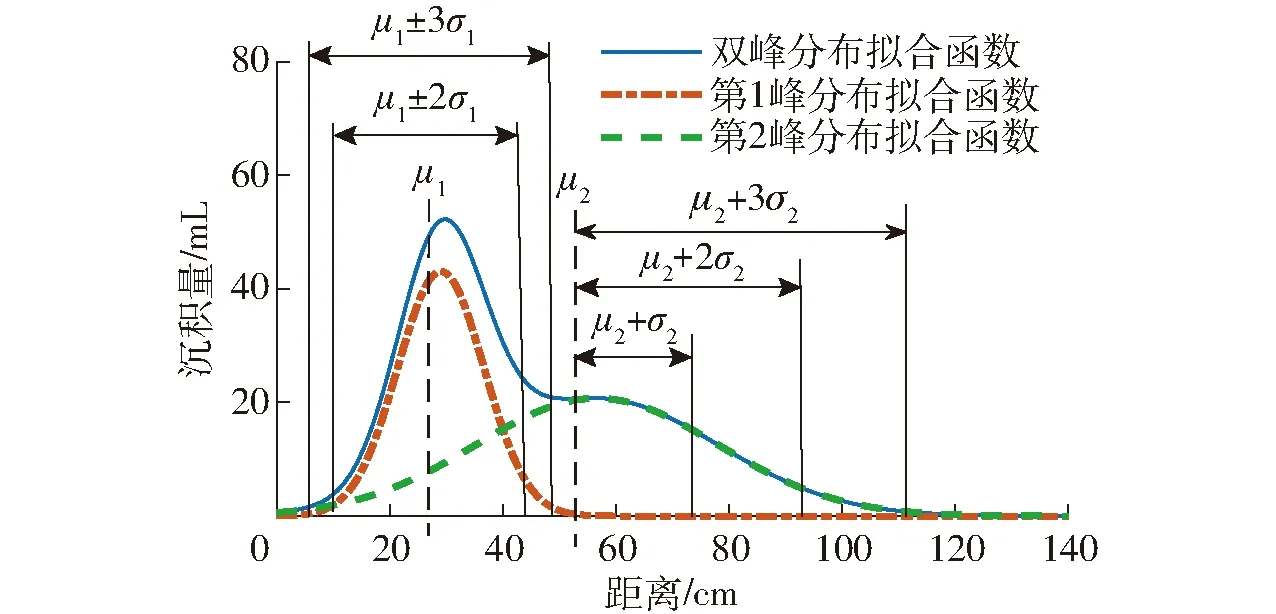
图6 沉积区域示意图Fig.6 Schematic of deposition range

3 试验结果与分析

3.1 试验方案与结果

根据Box-Benhnken试验方案，设计了三因素三水平的响应面分析试验，共17个试验点，其中包括12个分析因子和5个零点估计误差。每个试验点进行3次试验，取其平均值，并按照式(13)进行拟合，得到6个沉积分布参数的响应值。表6为响应面试验设置与试验结果。

表6 试验设计方案与响应值结果Tab.6 Experiment design and response values

3.2 响应显著性与分析

以表6中的17组试验数据为基础，运用Design-Expert软件拟合喷雾参数与双峰分布模型中参数的响应关系。建立双峰分布模型，以及两个峰值的质量参数、位置参数和尺度参数与横风风速、喷雾高度和喷雾压力的二次回归模型。通过F检验得到P值以确定各个因素对响应值的影响显著性，如表7所示。

由表7可以看出，各变量对两个分布的相同性质参数有不同的影响。第1峰值分布沉积量参数k1影响极显著的因素是喷雾高度，对第2峰值沉积量参数k2影响极显著的因素是喷雾压力，显著因素是横风风速，而k1的极显著因素喷雾高度是k2的不显著因素。第1峰值的尺度参数σ1受到v、H、p影响都极显著，说明第1峰值的分布范围受到多个因素影响，而第2峰值的分布范围σ2只有喷雾高度是极显著因素。对于2个峰值分布的位置参数μ1、μ2，喷雾高度、喷雾压力、横风风速都是其显著影响因素。二次回归模型各项参数如表8所示。

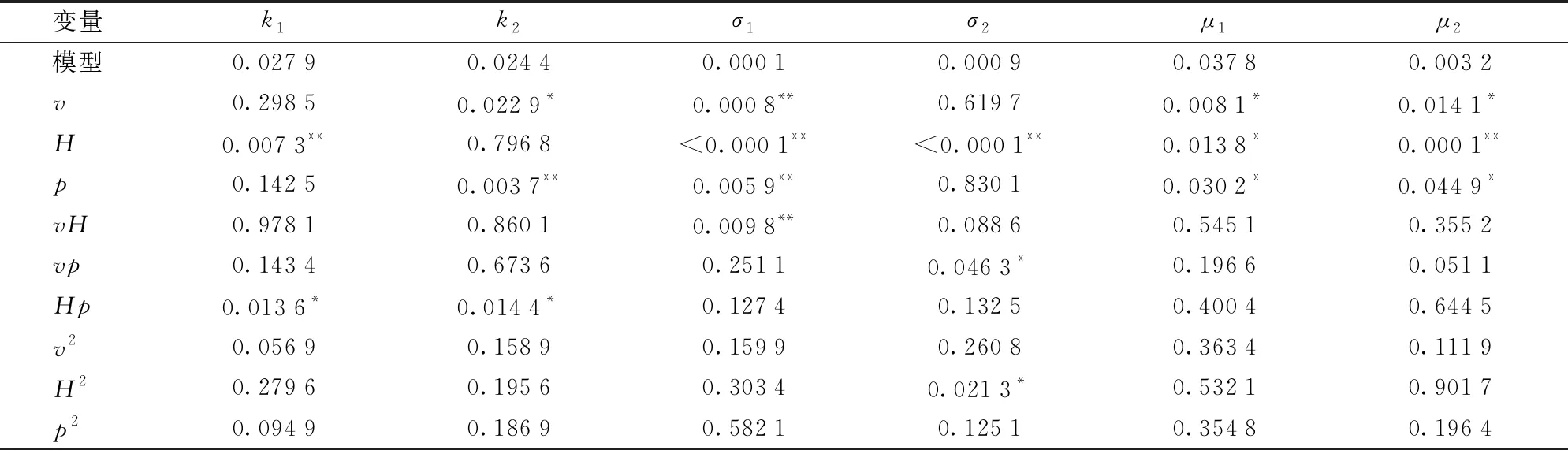
表7 响应显著性P Tab.7 Response significance P value

注：** 表示差异极显著(P<0.01)，*表示差异显著(P<0.05)。

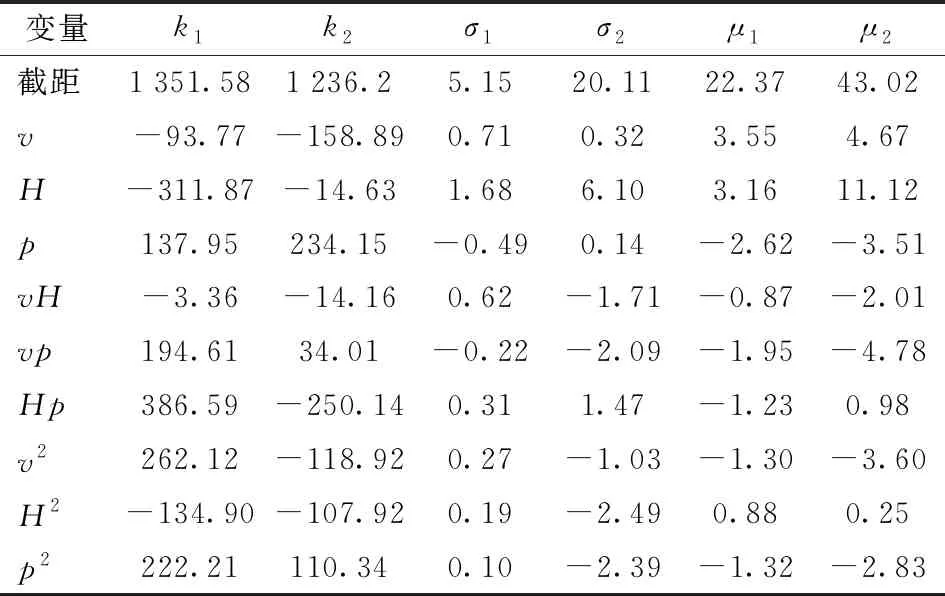
表8 二次回归模型参数估值Tab.8 Coefficient estimation of quadratic regression model

由表8确定各个双峰分布模型参数的回归方程，并根据方程绘制各个参数的变化云图。

3.3 各因素对模型参数的影响

根据各个参数的二次回归模型，绘制在不同影响条件下的参数云图。通过三维云图，可以直观地展现各个参数随影响因素变化的趋势。

3.3.1对质量参数的影响

沉积量参数k反映了两个峰值分布的雾滴沉积量，其变化规律如图7所示。当有横风时，因受到流场影响的程度不同，一部分雾滴从原本的雾滴群粒子中分离出去，成为具有不同性质的第2雾滴粒子群。此雾滴粒子群的沉积产生了第2峰值沉积量的分布。喷头喷出的总量在2个峰值分布中进行了分配，一方沉积量增加则另一方沉积量减少。k1越大则说明整体沉积分布越集中；k2越大则说明雾滴沉积在尾部的量越多，飘移更加明显。第1峰值沉积量参数k1在低风速、低压力、低高度的情况下较高，而k2则较低，此情况下飘移较少，喷出雾滴质量基本集中于第1峰值分布。随着喷雾高度和横风风速的增加，质量开始向第2峰值转移。

图7 沉积量参数三维云图Fig.7 Three-dimensional cloud maps of sedimentation parameters

图8 位置参数三维云图Fig.8 Three-dimensional cloud maps of position parameters

3.3.2对位置参数的影响

位置参数μ反映了两个峰值分布的集中位置，是两个分布的中位数和均值，表示双峰分布偏离喷头位置的水平距离，其变化规律如图8所示。两个分部的雾滴粒子群具有相同的变化趋势，均随着喷雾高度、喷雾压力和横风风速的增大而偏移距离增大。在高喷雾压力、高喷雾高度和强横风的情况下，双峰位置发生的偏移最大，第1峰值分布最大位移为33 cm，第2峰值分布最大位移为59 cm。随着风速增大，μ1受到喷雾高度影响减小；而μ2随着喷雾压力的增大而减小。当喷雾高度H≤30 cm时，出现μ1≤μ2的情况，说明两个峰值出现了重合情况。

3.3.3对尺度参数的影响

尺度参数σ反映了两个峰值以μ为中心的分布范围。σ越大，说明沉积量越分散，峰值分布范围越大；σ越小，说明沉积量越集中，峰值分布的范围越小。其变化规律如图9所示。两个峰值的分布范围皆随着喷雾高度和横风风速的增大而增大。其中σ1随着喷雾压力的增大而减小，而σ2在低风速时受其影响较小，随着风速增大，σ2呈现出与σ1相同的变化规律。当v=4 m/s、H=50 cm、p=0.2 MPa时，σ1取得最大值12 cm。当v=4 m/s、H=50 cm、p=0.5 MPa时，σ1取得最大值25 cm。当v=1 m/s、H=20 cm、p=0.8 MPa时，出现最小值σ2min=2 cm。在H≤30 cm时，σ2出现接近0 cm的情况，其区域与μ1≤μ2的区域一致，说明第2峰值分布被第1峰值分布包含。

4 结论

(1)在有胁迫气流场的情况下，多峰分布式可以较好地描述雾滴沉积分布(R2≥0.99)，随着峰数的增加，模型拟合度提高，随着横风风速的增大，拟合度降低。以双峰分布数学模型描述雾滴在横风风速不大于3 m/s时的沉积分布情况，其拟合决定系数均大于0.95，说明拟合效果较好。

(2)不同因素对两个峰值分布的相同物理意义的参数的影响显著度不同。模型本身的双峰值是两个分布的沉积量分割，两个峰值分布可以分别体现出雾滴飘移分布的集中性和重尾性。

(3)第1峰值分布和第2峰值分布的沉积量(沉积量参数k)变化趋势相反，表现为两个分布间的沉积量转移。第1峰值沉积量最大值和第2峰值沉积量最小值都出现在低喷雾高度、低喷雾压力时段。因此，在横风存在的情况下，为使药液质量沉积更集中、尾部沉积质量更少，应采取低作业高度，减少喷头到靶标的距离，降低喷雾压力。第1峰值和第2峰值分布的位置(位置参数μ)变化具有相同趋势，均随着风速、高度的增加而增大，随喷雾压力的增加而减小，因此，增大喷雾压力可以减小中心飘移距。第1和第2峰值分布的范围(尺度参数σ)都随着喷雾高度和风速的增加而增加，沉积量分布更加分散。增大喷雾压力可以有效减少第1峰值的沉积量分散，但对第2峰值分布无影响。

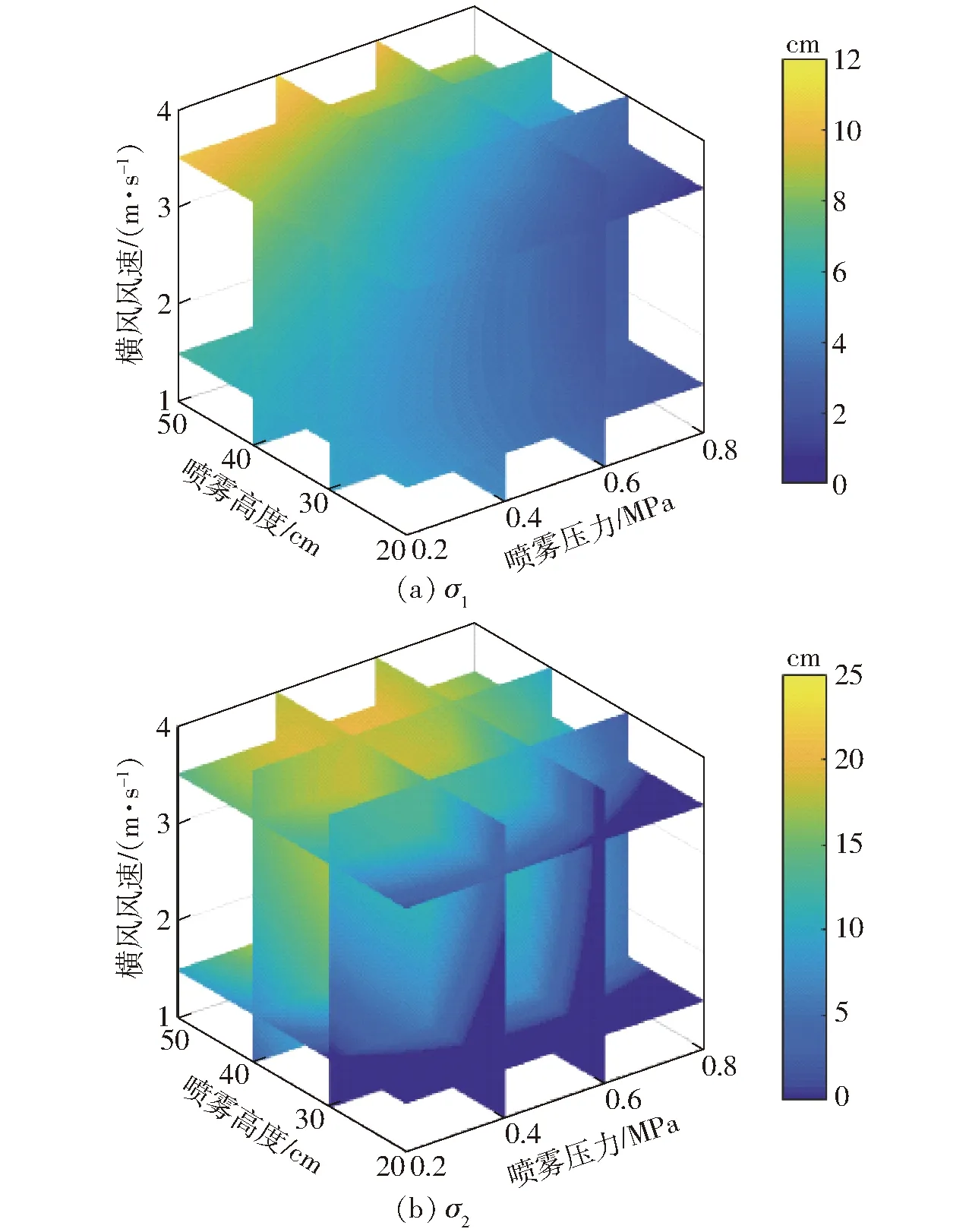
图9 尺度参数三维云图Fig.9 Three-dimensional cloud maps of scale parameters