基于双频外差和相移法的结构光成像包裹相位解调算法

谷倩倩，吕珊珊，姜明顺，张 雷，张法业，隋青美

(1.山东大学控制科学与工程学院，山东济南 250061;2.山东大学海洋研究院，山东青岛 266237)

0 引言

光栅投影三维测量技术凭借其非接触、快速、精确度高等优势迅速发展，被广泛应用于工业自动化、生物医疗等研究领域，其基本原理是通过提取变形光栅条纹中的相位信息来实现三维测量，而通过相移法只能得到包裹在［－π，π］范围内的相位主值，不具有唯一性，所以必须进行相位展开得到连续分布的绝对相位［1－3］。

相位展开算法分为空域相位展开算法和时域相位展开算法两大类［4］。空域相位展开算法依靠空间相邻像素点之间的相位值恢复绝对相位，存在相位突变现象，从而导致错误累积，不完全可靠。时域相位展开算法是将每个像素点的相位值进行独立计算，可以有效避免错误累积，常用的有格雷码法和多频外差法。格雷码法所需投影条纹数目较多，操作复杂，存在周期错位现象［5］;多频外差法所需投影条纹数目相对较少，不存在周期错位现象。

针对上述问题，本文采用双频外差和四步相移相结合的方法来实现相位解调。通过向被测对象投射2组不同频率的光栅图像，首先由四步相移法求得相位主值，再通过双频外差法进行相位展开，求取绝对相位，该方法减少了投影光栅条纹数目，加快了测量速度，避免了错误累积和周期错位现象，同时保持了较高的相位解调精度。

1 相移法和多频外差法原理

1.1 相移法原理

相移法通过投影多幅具有相同相位增量的标准正弦光栅图像到被测对象表面，光栅图像的相位受到被测对象表面高度的调制会发生形变，对采集到的变形光栅图像进行分析处理即可得到其相位主值分布［6］。下面以标准四步相移法为例说明其测量原理，经被测对象调制后的变形光栅图像光强可表示为

式中:Ii(x，y)为第i幅光栅图像的光强分布;a和b分别为背景光强和调制光强;φ(x，y)为点(x，y)处的相位主值;δi为第i幅图像的相移值。

在理想情况下，投影出的光栅图像的光强也应该符合标准正弦分布。在利用四步相移法计算光栅图像的相位主值时，每步相移量为π/2，即需要投射4幅相移值分别为0，π/2，π，3π/2的光栅图像，其光强表示如下:

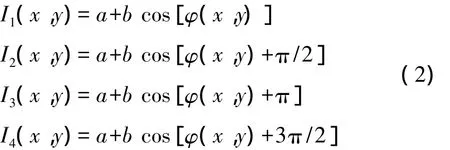
联立上述的4个方程可得其对应的相位主值为

由式(3)以及反正切函数的性质可知，此时得到的相位主值在［－π，π］范围内呈锯齿形分布，必须进行相位展开操作才能得到连续分布的绝对相位。

1.2 多频外差法原理

多频外差法通过多个不同频率(周期)正弦光栅图像的相位值作差，将小周期的相位主值转变为大周期的相位差，并使相位差信号覆盖整个测量视场，再根据相位差与绝对相位之间的关系即可求得光栅图像的绝对相位分布［7－9］。以双频外差为例，其原理如图1所示。

图1 多频外差法原理图

取周期分别为T1和T2的正弦光栅图像进行实验，其对应的相位主值分别为φ1和φ2，绝对相位分别为Φ1和Φ2，且T2＞T1。经过双频外差法，两者的相位差φ12及其周期 T12可由如下公式表示:

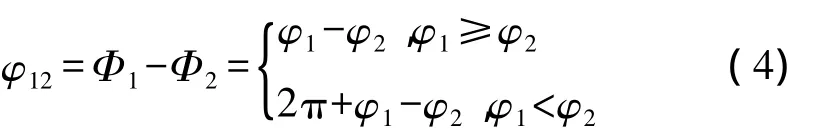
为了能够利用多频外差原理实现全场无歧义的相位展开，必须选择合适的T1、T2使得相位差函数的周期T12大于整个测量幅面，即在整个周期内φ12单调增长。

在相机、投影仪以及被测对象相对位置不变的情况下，根据图像上同一点在光栅图像上的位置也相同，可得周期T1、T2下绝对相位Φ1、Φ2之间有如下关系:

联立式(4)和式(6)，可得相位主值φ1对应的绝对相位:

或

式中:round(x)为就近取整;m为该点所属的条纹周期数。

2 实验与讨论

2.1 测量系统结构

光栅投影三维测量系统由光栅投影装置、图像采集装置、控制与数据处理装置以及被测对象4部分构成，其结构简图如图2所示。

图2 光栅投影三维测量系统结构简图

采用数字投影仪(型号:IN2128HDx，分辨率:1920×1080)作为光栅投影装置，按照需求将具有一定相位差的正弦光栅图像按顺序投影到被测对象表面，实现相移;采用相机(型号:MER－500－14GM，分辨率:2 592×1 944)作为图像采集装置，获取经被测对象调制的光栅图像并传输至计算机;计算机作为控制与数据处理装置，一方面控制相机采集光栅图像，另一方面对采集到的数据进行分析与处理。

2.2 相位解调实验

采用四步相移法和双频外差法相结合的方法进行相位解调，以一个正方体作为被测对象，如图2所示。其中A～H分别表示正方体的各个顶点，O为相机出入射光瞳的中心，以正方体的棱BF为中心进行投影，平面BOF垂直于平面AEGC，平面BOF垂直于平面EFGH。

首先通过MATLAB软件生成周期T1=50 pixel、T2=51 pixel的正弦光栅图像，如图3所示。根据式(5)得相位差函数周期T12=2 550 pixel，即理论测量范围为2 550 pixel，实际测量范围大小受投影仪、相机以及被测对象之间的对应关系影响。

图3 投射的正弦光栅图像

通过投影仪将正弦光栅图像投射到正方体表面，由相机采集经正方体调制后的光栅图像并返回到计算机，由于外界环境因素会导致采集到的光栅图像存在噪声干扰，故先通过MATLAB软件对其进行滤波处理，处理后的变形光栅图像如图4所示。

图4 滤波后的变形光栅图像

根据式(3)求相位主值φ1、φ2，其分布情况如图5所示。

由图5可知，相位主值φ1、φ2仍存在明显的背景噪声，故分别求其对应的σ，选取合适的阈值，将σ小于阈值的像素点对应的相对相位置为－π。σ第600行的分布情况如图6所示，分析图6可知当阈值等于0.002时，可将背景噪声完全滤除，故设置阈值为0.002。

图5 相位主值分布图

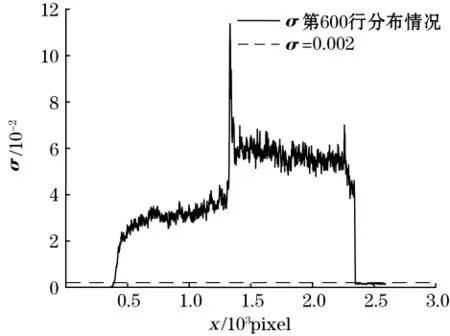
图6 σ第600行的分布情况

通过上述操作滤除背景噪声，得到校正后的相位主值φ1、φ2及其第1 000行的相位分布情况如图7所示。

根据式(4)，由校正后的相位主值 φ1、φ2求得相位差φ12及其第1 000行的相位分布情况如图8所示。由图8得，当T1=50、T2=51时，相位差φ12可以覆盖整个测量视场，满足实验条件。

分别通过2种方法由相位差φ12求得绝对相位Φ1，方法一采用式(7)直接计算，方法二采用式(8)、式(9)得到绝对相位。2种方法求得的绝对相位Φ1第1 000行的相位分布对比情况如图9(a)所示。由图9(a)可知，采用方法二求得的绝对相位分布更平滑，精确度更高。

通过空域相位展开法求取绝对相位，其第1 000行相位分布情况如图9(b)所示。

将双频外差法与空域相位展开法求得的绝对相位Φ1进行对比，其第1 000行相位分布对比情况如图10所示。

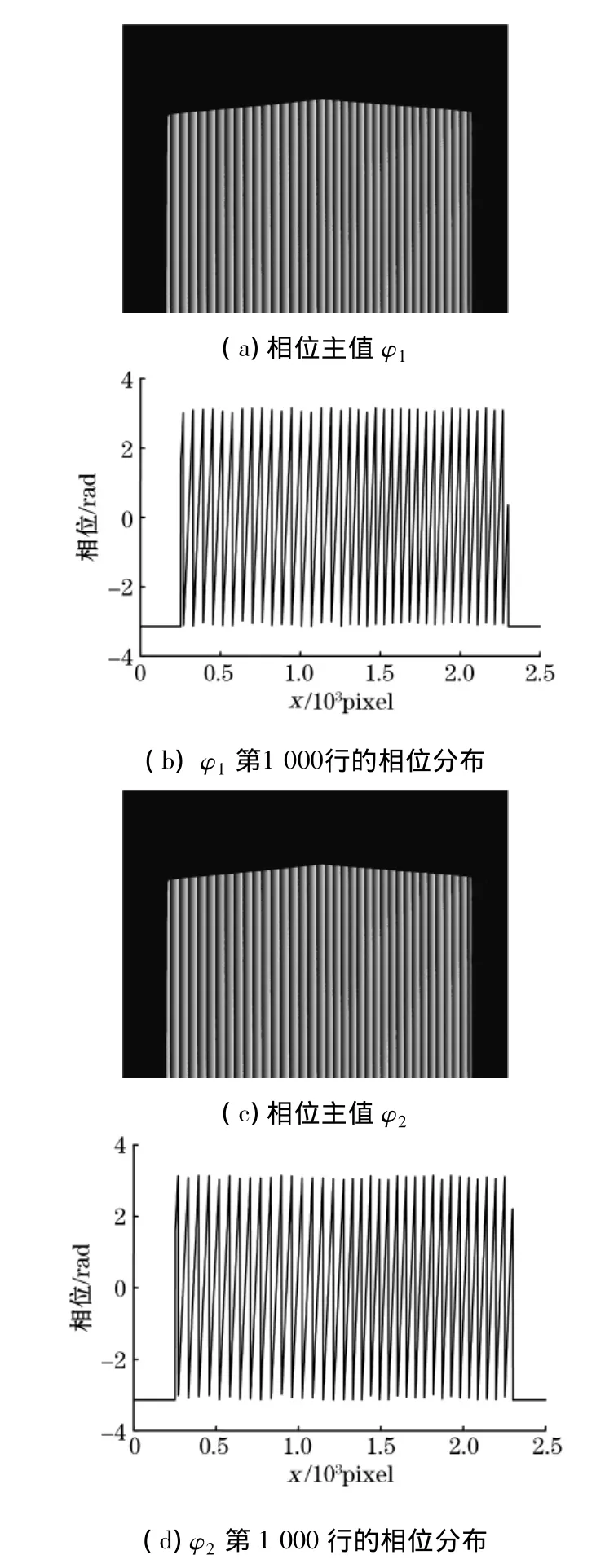
图7 校正后的相位主值φ1、φ2及其第1 000行的相位分布情况

2.3 实验结果分析与讨论

实际测量中，光栅图像受到物体表面高度调制，使得采集到的变形光栅图像周期T为变量，故在双频外差法中由方法一求得的绝对相位Φ1与其实际值之间存在误差，方法二通过取整操作对由方法一导致的相位误差进行校正，分析图9(a)可知，该方法较好地修正了变形光栅图像周期非常量导致的相位误差。

由图9(b)得，本次实验由空域相位展开法得到的绝对相位不存在解相错误，故其结果具有较高的测量精度，将双频外差法求得的绝对相位Φ1与不存在解相错误的空域相位展开法的实验结果进行对比分析，结果如图10所示，因此可得双频外差法的相位解调精度也较高，同时可以很好地避免空域相位展开法中由外界环境因素或被测对象自身的不连续性导致的错误累积。

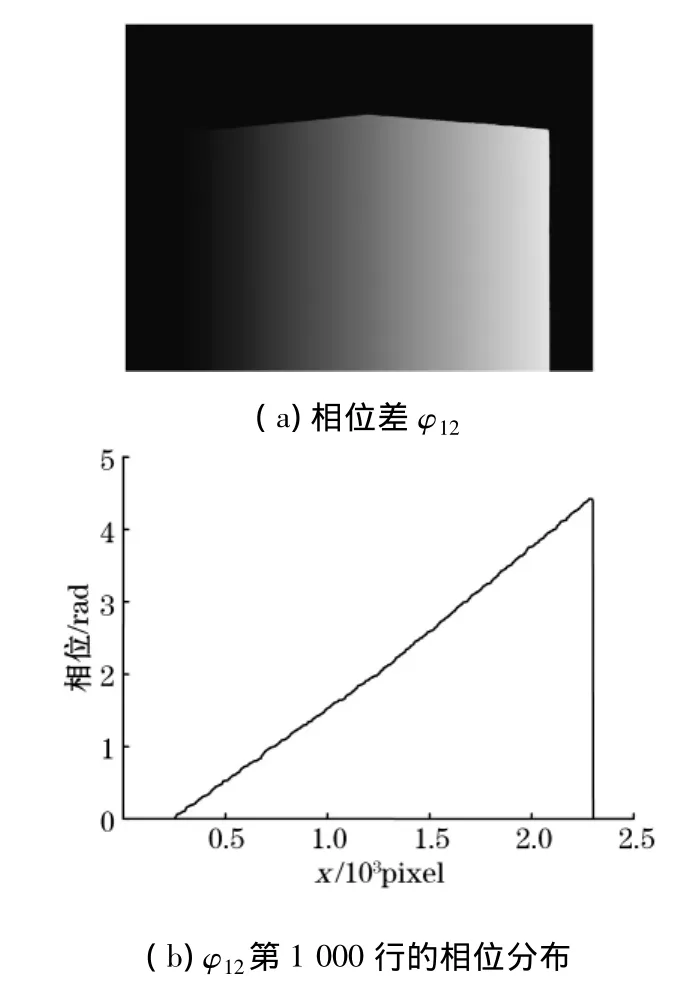
图8 相位差φ12及其第1 000行的相位分布情况

图9 绝对相位Φ1第1 000行的相位分布情况对比

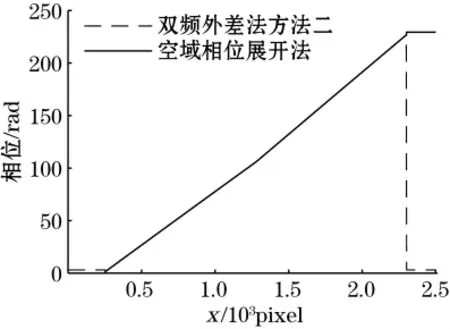
图10 双频外差法与空域相位展开法实验结果对比

3 结论

通过将正方体作为被测对象，采用双频外差和四步相移法相结合的方法进行相位解调实验，一方面证明了双频外差法由相位差求取绝对相位的过程中，取整操作可以较好地修正实际测量中采集到的变形光栅条纹周期非常量导致的相位误差;另一方面通过与不存在相位解调错误的空域相位展开法得到的实验结果进行对比分析，证明了基于双频外差和相移法的结构光成像包裹相位解调算法具有较高的可行性并且具有较高的相位解调精度，除此之外还有效避免了因环境因素以及被测对象本身的不连续性导致的相位解调错误，更加准确可靠，同时具备所需投影光栅条纹数目相对较少，测量速度快的优点。