一种多自由度-刚柔耦合筛分机械的构型设计与分析
2020-04-26李海波赵学清耿葵花
李海波,赵学清,耿葵花
1张家界航空工业职业技术学院 湖南张家界 427000
2广西大学 广西南宁 530000
振动机械在矿山、冶金、军工等领域有着非常广泛的应用,利用振动特性来满足生产中工艺过程和工作过程的要求,目前国内外许多企业和学者致力于筛分系统的研究,并取得了丰硕的成果。例如,美卓集团研发的 Ripl-Flo 圆形振动筛,激振力由偏心轴和外置式偏心块产生,筛面还可根据需要分为 1~3 层;山特维克公司研发了最新的 SC 系列圆形振动筛,其振动强度可达 4.5 G[1]。同时较早前有学者提出利用液压系统提供激振力的构想,如前苏联学者V.K.Astashev 等研发了一种新型机械振动系统的液压激振器,其原理建立在液体流经振动体通道时的动态影响;日本学者 Y.Sasaki 提出了一种由 1 个比例螺旋阀和 1 个高速启闭的螺旋阀控制 2 个单杆活塞的液压振动系统,并研究通过调节压力、频率和电压等来实现对振频、振幅等参数控制[2]。
相较于国外,我国在该领域的研究起步较晚,不过发展速度很快。如江苏大学的王成军等人[3]提出了一种三自由度混联振动筛,能实现筛箱沿x、y、z3个方向的振动;安徽理工大学王增一等人[4]研发了一种三自由度混沌振动筛,将混沌振动理论用于筛分机械中。但目前的筛分装置仍存在诸如筛面运动形式简单且独立、忽略了多自由度间的强耦合效应、不注重筛分节拍的柔性调节等不足。为此,笔者提出了一种强耦合、节拍可调且刚柔并举的筛分机构,在完全解耦的基础上对筛面上各点非规则水平和竖向运动规律进行了解析,并结合多体软件分析了关键因素与功能参数间的相关性,所得结论可为同类机构的设计和应用提供参考。
1 筛分机构的构型设计与分析
1.1 总体结构
多自由度-刚柔耦合筛分机构左右两侧对称,整体结构模型如图 1 所示,包括筛面、水平筛分运动和抛掷运动驱动机构以及两者的耦合连接机构 4 个主要部分。其中筛面为末端执行件,水平与竖向驱动机构间通过同步带系统耦合,竖向驱动机构包括曲柄摇杆机构和与连杆铰接的顶杆及滑块,滑块在筛面右侧的滑槽中移动;水平驱动机构由行星驱动轮系和推杆组成,推杆的前端与筛面左侧下端通过弹簧形成柔性连接。

图1 振动筛分装置的整机结构示意Fig.1 Structural sketch of vibratory sieving device
1.2 工作原理与设计分析
本构型的筛分动作由抛掷和水平筛分运动驱动机构协同完成,其中抛掷运动驱动机构的曲柄为原动件,连杆与顶杆铰接,顶杆另一端驱动滑块往复移动,同时滑块使筛面绕水平推杆的前端作变速转动;主同步带轮通过从同步带轮驱动水平筛分运动驱动机构使筛面作往复移动。
筛面的俯仰运动不断将物料抛向水平驱动机构一侧,块状物料在与机体的撞击中破碎,粗细颗粒在筛面的往复运动中析离;又由于同步带轮系统的传动比可依需要进行调整,行星轮自转与公转是同步进行的;因此,筛面的运动实质为驱动杆长不断变化的正弦机构驱动的水平运动,适当地选择同步带轮系统的传动比可改变单个周期内筛面俯仰与往复运动的频次。
2 筛分机构的运动形态分析
2.1 水平筛分的运动形态与相关参数
水平筛分机构的运动如图 2 所示,图 2 中各主要参数的含义如表 1 所列。

图2 水平筛分机构运动示意Fig.2 Kinematic sketch of horizontal sieving mechanism

表1 主要参数符号和含义Tab.1 Symbols and meanings of main parameters
由行星轮系的相关理论不难求得
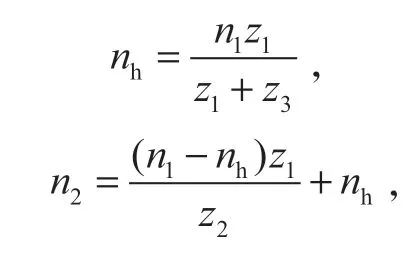
式中:n1、n2分别为中心轮、行星轮的转速,r/min。
以图 2 中 ΔHO1J为研究对象,由余弦和正弦定理得
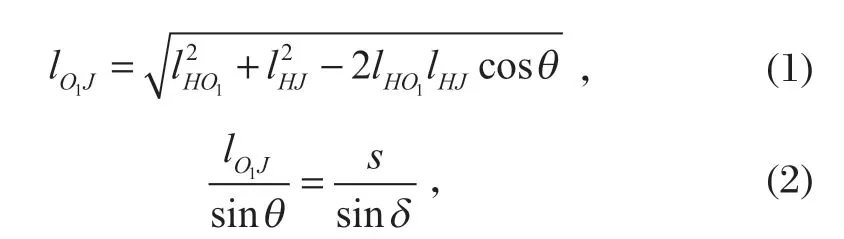
式中:θ为lHO1和lHJ之间的夹角;δ为lHO1和lO1J之间的夹角。
进而可求得

由式(1)、(3)可求得lO1J在x轴上的投影为
综上所述,基于当前证据,在临床疗效方面,针刺治疗效果优于中成药、西药疗法、中药坐浴和微波疗法,而与服用中药汤剂治疗比较疗效差异不具有显著性;在降低NIH-CPSI评分方面,针刺治疗均较服用西药治疗、微波疗法与假针刺治疗效果好;在白细胞降低有效率方面,针刺治疗较中药坐浴疗法的治疗效果好,但与服用西药治疗的疗效相同。
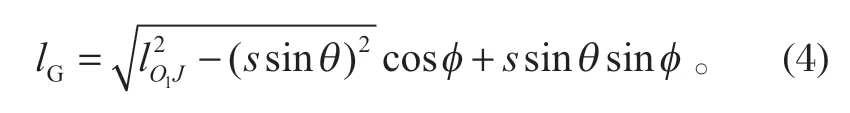
若中心轮顺时针方向旋转,随后系杆H与x轴间的夹角变化为φ-(dφ/dt),则可根据行星轮系的传动比关系求得lHO1和lHJ之间的夹角变化为

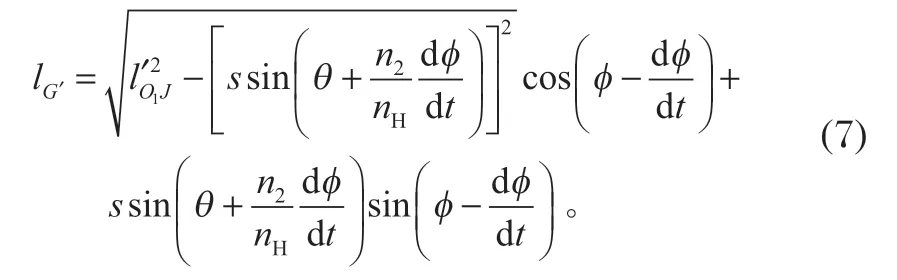
则可求得水平推杆前端G点的水平位移

2.2 变距抛掷的运动形态与相关参数
对于某些结块的物料而言,抛掷运动所产生的撞击力使筛面上的料层呈松散状态,同时保持细颗粒透筛通道的畅通。笔者以曲柄摇杆机构为驱动力源,滑块的往复运动使筛面绕水平推杆的前端作变速转动,从而实现抛掷运动形态,其运动简图如图 3 所示,各主要参数含义如表 2 所列。
根据图 3,结合曲柄摇杆机构等相关计算理论分析后可求得
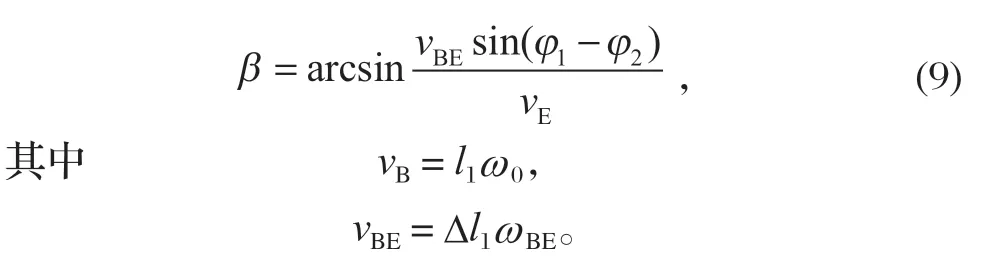
根据图 3 中B、E、F这 3 点的几何位置关系可求得
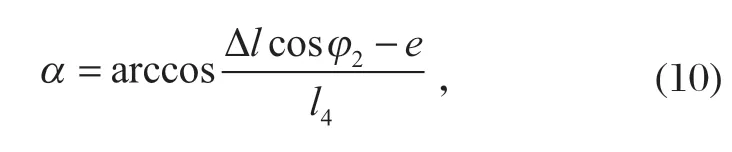
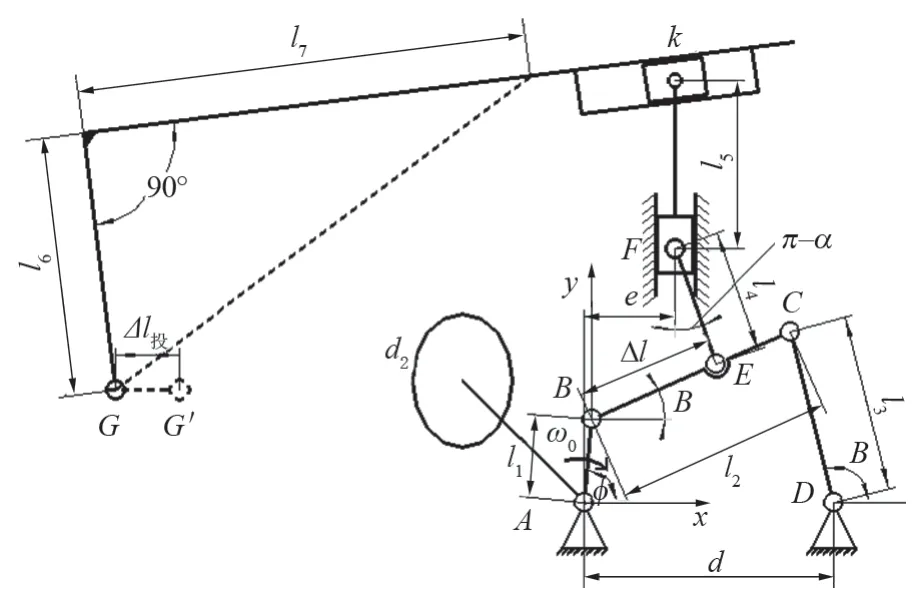
图3 抛掷运动机构的运动示意Fig.3 Kinematic sketch of throwing mechanism
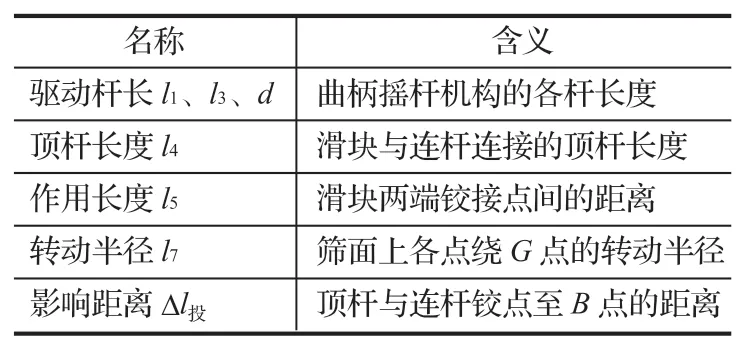
表2 主要参数符号和含义Tab.2 Symbols and meanings of main parameters
根据几何关系及相关定理不难得出

将vF沿直线KG和NK方向分解后可求得垂直于直线KG方向的速度分量,即为筛面上任意一点绕G点旋转的线速度
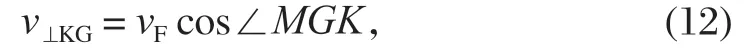
于是筛面任意点绕G点旋转的角速度

物料颗粒在筛面上的受力情况如图 4 所示。

图4 物料颗粒在振动筛上的受力状态Fig.4 Force state of particles on sieving screen
图4 中,N为筛面对物料的法向反力;F为筛面对物料的静摩擦力;ξ为筛面倾角;η为筛箱运动的相位角;ψ为筛箱的跳动方向角;δ为物料的跳动角。
由图 4 可得,颗粒抛掷运动的条件为∑Fy=0,即颗粒给筛面的正压力N=0。

变换后可求得
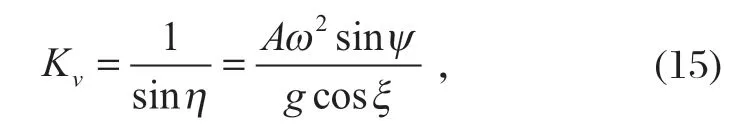

结合式(13),可求得振动筛的振幅
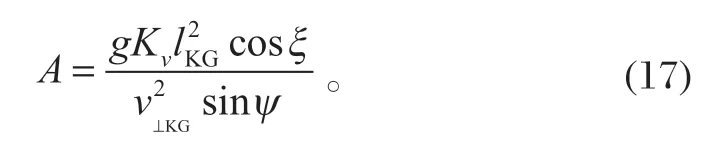
从式(17)可知,振动筛的振幅与曲柄摇杆机构各杆的尺度关系密切相关(主要影响v⊥KG),同时增加筛面的长度尺寸(K、G两点距离)可显著增加筛面振幅。
3 不同因素对振动筛运动特性的影响
3.1 建立虚拟样机
本构型抛掷和水平筛分运动驱动机构是影响筛面运动形态的主要因素。筛分构型两侧具有完全空间对称性,根据所建立的运动简图,建模时只反映与筛面运动特性有关的结构特征与尺寸即可,仿真模型如图5 所示,模型的约束类型如表 3 所列。
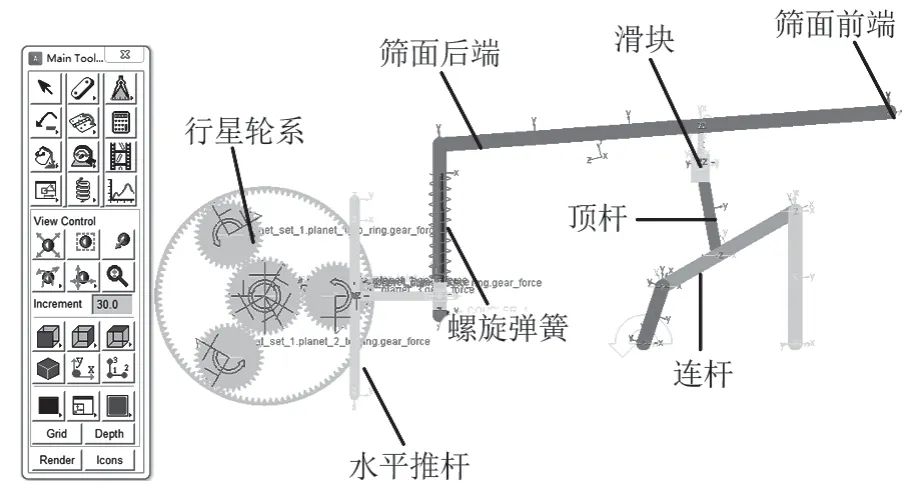
图5 多自由度筛分构型的仿真模型Fig.5 Simulation model of multiple DOF sieving configuration

表3 仿真模型的约束类型Tab.3 Constraint types of simulation model
3.2 仿真分析
调用 ADAMS/Solver 进行仿真分析获得各构件的运动特性,设置仿真时间 End time 为 5 s,步数为1 000,驱动杆的移动函数为 15 d*time,然后进行仿真,仿真结束后进入 PostProcessor 进行后处理。
3.2.1 耦合传动比对振动筛面运动轨迹的影响
抛掷和水平筛分驱动机构的耦合传动比是影响筛面运动协同形态的主要因素,其对筛面前端点运动轨迹的影响如图 6 所示。
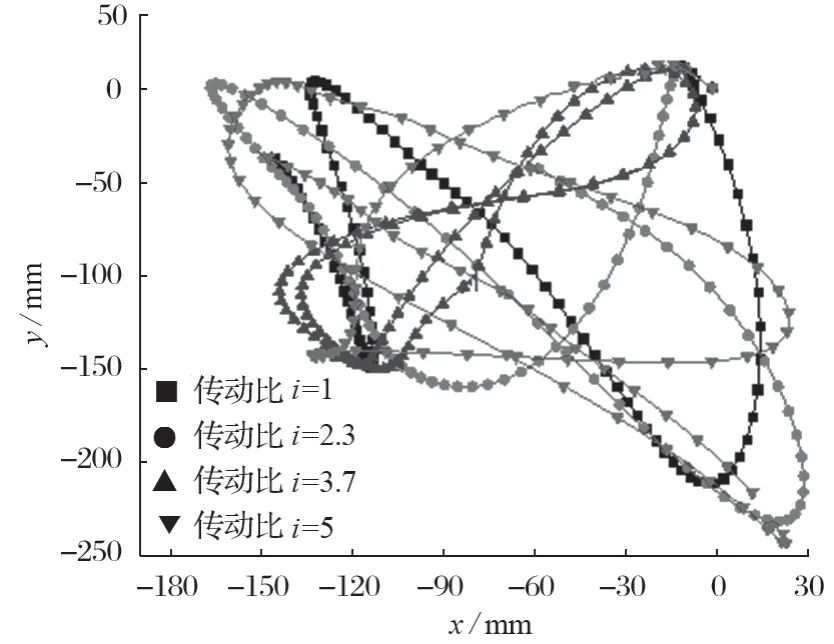
图6 不同传动比时筛面前端点的运动轨迹Fig.6 Motion trajectory of front end point of sieving surface at various transmission ratio
图6 表明:耦合传动比对筛面运动形态具有非常明显的影响,体现了本构型对筛分运动灵活的调节能力。传动比i=1 和 2.3 时,筛面前端点运动轨迹向左偏移且不完整,筛面回筛路程短,向下倾斜的时间较长,不利于给筛面上的物料提供足够的留筛时间;i=3.7 时,筛面运动轨迹完整,呈向右倾斜的“8”字形,筛面下俯和上仰的时间趋于相等且较平缓,在轨迹两端方向转换无突变,筛面的运动形态较好;当i=5 时,筛面运动轨迹为向左倾斜的腰形,轨迹不完整且存在突变,筛面运动形态不如前者。因此分析表明,耦合传动比能显著地影响筛面的运动形态,可依托现代传动技术对筛面运动形态进行无级调整,以获得最佳筛分轨迹形态。
3.2.2 筛面与水平推杆连接方式对筛面振幅的影响
筛面的振幅是影响结块物料的破碎和粗细颗粒重新分布的重要影响因素,筛面与水平推杆刚性与柔性连接 2 种方式对筛面振幅的影响如图 7 所示。
由图 7 可知:无论采用刚性连接还是柔性连接,筛面的振幅均体现了近简谐运动的特性,且筛面的振动周期基本相同;与柔性连接相比较,采用刚性连接时筛面的振幅整体偏低,且在振幅峰值处体现更为明显。因此,筛面与水平推杆连接方式对筛面振幅有很大影响,采用柔性连接且降低刚性系数有助于提高振动筛的抛掷能力。
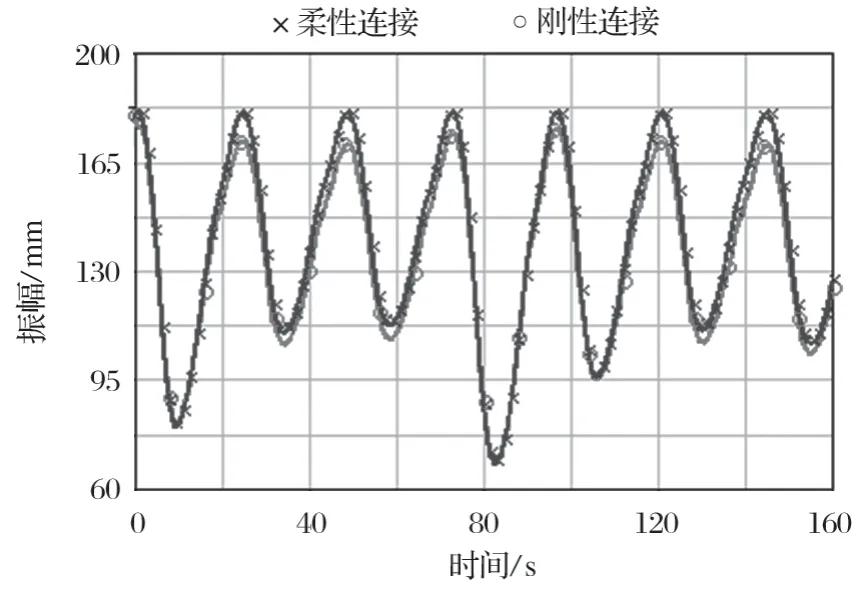
图7 柔性与刚性连接时筛面振幅曲线Fig.7 Amplitude curve of sieving surface in flexible and rigid connection mode
4 结论
(1)通过对构型特征的分析表明,本构型通过水平往复和抛掷运动的协同完成筛分动作,运动间通过传动比耦合,为筛面运动学参数的调整提供了灵活的空间,同时便于实现无级调整;其次,通过计算表明,增加筛面的长度尺寸(K、G两点距离)可显著增加筛面振幅。
(2)仿真分析表明,耦合传动比对筛面的运动形态具有显著的影响,耦合传动比为 3.7 时振动筛的运动形态较好。
(3)筛面与水平推杆间采用柔性连接可提高筛面的振幅,且降低刚性系数,有助于提高振动筛的抛掷能力。
