弛张筛面大挠度非线性变形分析与实验

彭利平,刘初升,董海林,李 珺,夏云飞

(1.中国矿业大学机电工程学院,江苏徐州 221116;2.浙江中烟工业有限责任公司,浙江杭州 310000)

弛张筛面大挠度非线性变形分析与实验

彭利平1,刘初升1,董海林1,李 珺1,夏云飞2

(1.中国矿业大学机电工程学院,江苏徐州 221116;2.浙江中烟工业有限责任公司,浙江杭州 310000)

为研究高硬度弛张筛面挠曲运动过程中的大挠度非线性变形特性,考虑其受端部支承轴向压缩而失稳,建立了弛张筛面的细长压杆模型,引入换元积分,导出了筛面变形量随筛面长度的精确定量表达式,利用数值算法发现了筛板端部移动量应不大于0.271 5l(l为筛板长度);进行了筛面大挠度变形量的测试实验,发现变形筛面中心线两侧对称测点处的测量值十分接近,且筛面各测点处大挠度非线性变形的测量值和理论值的误差保持在7%以内,表明上述模型在表征筛面变形特性上的可行性。

弛张筛面;大挠度变形;非线性变形

选煤是洁净煤炭生产和高效利用最经济有效的办法[1]。受煤层渗水、井下防尘喷水和井下管理不当等因素的影响,原煤含水量往往在7%以上。这些潮湿细粒原煤在外在水分和黏土的共同作用下黏连成团并黏附在筛网上,影响筛分效率。当原煤外在水分达到7%～14%时,若进行3 mm或6 mm粒度分级,普通振动筛的筛分效率十分低下[2-4]。目前,弛张筛已经被工业应用证实是实现潮湿细粒煤炭的深度筛分的有效设备[5]。

弛张筛面运动特性的研究对筛面设计参数的确定具有重要意义:文献[6-7]基于弛张筛面的弹性压杆模型,利用线性解进行摄动逐次逼近的方法获得了小变形下筛面非线性动力学方程的解析表达式,理论分析结果与实测结果符合很好;文献[8]提出了弛张筛综合评价指数,从系统的观点分别对弛张筛的结构、工艺、动力学和运动学参数进行了优化,为提高产品的设计质量和运行水平指出了具体的改进方向;文献[9]利用弹性体振动模型研究了筛面张紧量对弛张筛动力学参数(加速度)的影响。

目前,弛张筛面的主要材料为聚氨酯,其突出问题是使用寿命短,选用硬度高的聚氨酯材料在一定程度上可以提高筛面的使用寿命,但是会使组合筛板间支撑座承受的作用力增大,且高硬度筛板在高频挠曲过程中,对支撑柱的横向交变剪力易使后者发生疲劳损伤。考虑到筛面厚度相对筛板长度较小,因此,可以将筛面等效成细长压杆。此外,由于筛面必须经历挠曲变形的过程,筛板在相对运动的端部支承作用下一直处于失稳状态。本文利用细长压杆失稳状态下的大挠度非线性变形模型来描述筛面变形与端部位移间的精确定量关系,并通过实验进行测试验证,为筛面设计参数的确定提供借鉴。

1 筛面大挠度非线性变形

1.1 模型的建立

传统的弛张筛筛面通过两端双板式横梁夹持固定在相对运动的筛体横梁上[10],较之而言,图1所示的半圆-板式横梁增加了下支撑梁的抗弯能力,增大了筛面的有效筛分长度,同时改变了其端部物理约束形式,类似简支,使筛面挠曲变形过程中筛面与下支撑横梁边缘的接触应力变化更为均匀[11-12],从而提高筛面的可靠性。筛面简支端同时向中心移动后,筛面变形如图2所示,在变形后筛面的初始端O′处建立如图2所示的坐标系,水平方向上距离O′点x处的弯曲筛面的下挠度为w。根据弹性杆件的稳定性理论,筛面变形的非线性方程[13]为

设u=dθ/ds,根据边界条件θ=θ0处有u=0,则式(1)化为u2=2k2(cos θ-cos θ0)。

由于筛面关于中心线对称,这里只研究中心线左侧的筛面变形。在筛面中心面在挠曲运动过程中长度保持不变的假设下[7],结合上式,有

图1 弛张筛面的半圆-板式夹持结构Fig.1 Semicircle-plate clamping mechanism for the flip-flow screen

图2 大挠度非线性形变的弛张筛面的力学模型Fig.2 Dynamic model for the flip-flow screen plane with the large nonlinear deformation

其中,F(a,π/2)=F(sin(θ0/2),π/2),F(a,φ)= F(sin(θ0/2),φ)分别为第1类完全椭圆积分和第1类椭圆积分[14]。根据式(6)和式(7),可以得到

式(6)表明,k仅与变形筛面的几何特性有关,为一定值,这一特性与式(1)中k一致;式(8)中,变形筛面曲面长度s由挠度发生位置A决定,当φ=0时θ=0,即筛面中点,此时s/l=0.5;而当φ=π/2时θ= θ0,即筛面端部,此时s/l=0。

设变形筛面上某一点与水平位置的距离(即该点筛面挠度)为w,与变形筛面起点的水平距离为x,根据图2所示的微元假设关系:dx=dscos θ,dw= dssin θ,并将式(5)代入得到

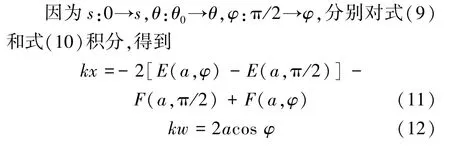
式中,E(a,π/2),E(a,φ)分别为第2类完全椭圆积分和第2类椭圆积分[14],E(a,π/2)=E(sin(θ0/2), π/2),E(a,φ)=E(sin(θ0/2),φ)。

将式(6)代入式(11),(12),两式均可转化为无量纲形式,即

这里考虑一半筛面的情况。假设筛面端点O位置未移动,则未变形筛面(图3中曲面Ⅰ)中点A在筛面变形(图3中曲面Ⅱ)后的位置为A″,而实际上由于筛面两侧同时同步移动,故筛面变形后中点A在竖直方向上不发生偏移,即处于图3中A′的位置。因此,筛面Ⅱ向右移动λ0后得到的才是真正的变形筛面,即图3中的曲面Ⅲ。

因此,结合式(13)和关系式a=sin(θ0/2),当给定简支端移动的距离λ0时,解式(15)的非线性方程可以得到筛面端部的初始变形角度θ0。

1.2 数值仿真

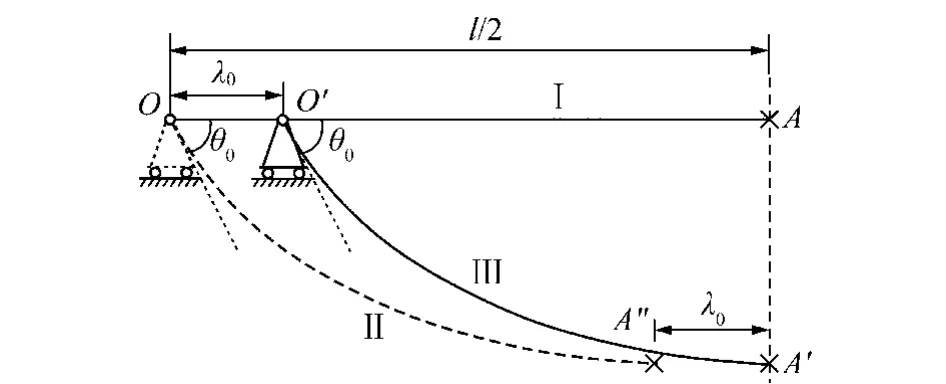
图3 弛张筛筛面简支端移动Fig.3 Movement of the simple support end of a flip-flow screen

上述筛面大挠度变形的模型分析过程中,由于椭圆积分的引入,简支端移动的距离λ0与筛面端部初始变形角度θ0间具有复杂的非线性函数关系,由于解析解的复杂性,这里采用数值方法进行仿真。考虑到实际中为防止筛面兜矿,需θ0∈[0,π/2],这里采用一维搜索法[15],通过计算各等间隔θ0下的λ0值,绘制筛面端部初始变形角度与无量纲简支端移动的距离间的相互关系,如图4所示。

图4 挠曲筛面端部转角与无量纲端部移动距离的相互关系Fig.4 Relationship between the rotation angle and the dimensionless displacement of the end

可以发现,端部移动的初始阶段,端部转角变化较快,非线性关系强。随着移动距离的增大,两者近似线性关系。当λ0接近0.27l时,筛面端部初始角度已接近90°(具体地,λ0=0.271 5l时,θ0=90°),即图1的半圆-板式结构弛张筛面的两驱动端移动的最大距离需小于0.271 5l。

图5绘制了端部转角 θ0分别为0°,10°,30°, 50°,70°和 90°(对应 λ0/l分别为 0,0.003 8, 0.033 8,0.091 5,0.172 7和0.271 5)时筛面的几何变形图及端部放大图。筛面均关于直线x/l=0.5对称。随着端部移动距离的增大,端部转角增大,筛面整体挠度增大,非线性变形增强。在θ0=90°的极限位置,筛面中点挠度最大。

2 实 验

2.1 实验方案

图5 不同端部转角下的筛面变形Fig.5 Deformed screen surface under different rotation angle of the end

图6 实验装置Fig.6 Experiment apparatus

如图6所示,实验中采用了硬度为70HA的聚氨酯筛板一块,筛板尺寸400 mm×200 mm×5 mm。筛板通过图1所述的半圆-板式夹持结构固定在两直线轴承上,利用后者在导轨上的相对运动而实现筛面的挠曲运动。张紧情况下筛面支撑间距l=305 mm, 4个激光位移传感器(LDS,KEYENCE公司,测量范围为160～440 mm,测量分辨率为10 μm)通过传感器安装座布置在聚氨酯筛面的正上方,初始化静止状态下张紧筛面的变形测量值为0。为方便测试,实验中使左端直线轴承固定,仅移动右端直线轴承而使筛板从张紧面起向下挠曲。筛面变形量以电压信号的形式由NI公司的数据采集硬件系统c-DAQ采集并输入计算机中处理。

2.2 实验数据与分析

如图7所示,实验中以最左端固定的直线轴承为坐标原点,布置的4只LDS的位置坐标xC分别为72.00,114.00,167.50和205.20 mm,由于上述模型中建立的变形方程中变形筛面位置与起点的水平位移x在筛面中心线的左侧,因此,需要对LDS的位置坐标按下式进行坐标变换,即

图7 测点位置的坐标变换Fig.7 Coordinates change of the test points

在给定端部移动的距离λ0时,利用一维搜索法,按式(15)获得对应的端部转角θ0的逼近解(此过程中搜索范围可以由按图4的λ0-θ0关系进行缩减),将实验中LDS布置的位置坐标或变换的坐标xC代入式(13)中,采用一维搜索法获得变量φ的值,代入式(14)中,即获得基于模型的筛面测点位置挠度的理论值。利用该值与测量值进行比较以检验模型的准确性,见表1。

位于中心线(相对最左端的坐标为0.5l-λ0)两侧的测点处的测量值十分接近。以两端压缩量2λ0= 23.2 mm时的测点 C2和 C3为例,两侧点中心在x=(114.00+167.50)/2=140.75 mm处,与筛面中心(0.5l-λ0=140.9 mm)几乎重合,而两测点的测量值分别为52.349和52.589 mm,几乎相等,表明筛面变形的对称性。此外,从表1中也可以发现,筛面各测点处大挠度非线性变形的测量值和理论值的误差保持在7%以内(最大为6.786%),表明上述细长压杆模型在表征筛面变形特性上的可行性。

这里需要指出,根据图2弛张筛面大挠度非线性变形的力学模型可以获得筛面变形与移动端位移间的相互关系,进一步地,可通过端部移动距离对时间的函数以获得筛面变形随时间的速度和加速度关系,进而求得筛面振动幅值和频率。但是,由于非线性特性的存在,其间涉及循环搜索法解非线性方程,因此计算量很大。对于需要考察筛面的运动特性情况,文献[6]中采用的摄动法求解更合适。

表1 筛面各测点处大挠度非线性变形的测量值和理论值比较Table 1 Comparison of the experimental data and theoretical data for LNDoFSP

3 结 论

(1)考虑其受端部支承轴向压缩而失稳,建立了弛张筛面的细长压杆模型,研究弛张筛面挠曲运动过程中的大挠度非线性变形特性。

(2)推导了筛面变形量随筛面长度的精确定量表达式,利用数值算法发现了筛板端部移动量应不大于0.271 5l(l为筛板长度)。

(3)通过实验测试,验证了所建模型在表征筛面变形特性上的可行性,其理论结果可以为弛张筛面设计参数的确定提供借鉴。

[1] 赵剑锋.低碳经济视角下煤炭工业清洁利用分析及政策建议[J].煤炭学报,2011,36(3):514-518.

Zhao Jianfeng.Analysis and policy recommendation on coal industry clean-using from the perspective of low-carbon economy[J].Journal of China Coal Society,2011,36(3):514-518.

[2] Meinel A.Fine and very fine screening[J].AT mineral processing English Edition,2010,51(1):1-8.

[3] Dong H L,Liu C S,Zhao Y M,et al.Review of the development of dry coal preparation theory and equipment[J].Advanced Materials Research,2013,619:239-243.

[4] Liu K S.Some factors affecting sieving performance and efficiency [J].Powder Technology,2009,193(2):208-213.

[5] 巩 固,汤会锋.弛张筛在寺河矿选煤厂的应用[J].煤炭加工与综合利用,2013(1):30-32.

[6] Zhao Y M,Liu C S,Fan M M,et al.Research on acceleration of elastic flip-flow screen surface[J].International Journal of Mineral Processing,2000,59(4):267-274.

[7] 刘初升,赵跃民.弛张筛筛面动态特性及其筛分理论研究[J].煤炭学报,1998,23(4):426-430.

Liu Chusheng,Zhao Yuemin.Dynamic characteristics of flip-flow screen and screening theory[J].Journal of China Coal Society, 1998,23(4):426-430.

[8] 翟宏新,杨 丽,李 君.工业型弛张筛系统参数的整体优化[J].煤炭学报,2004,29(1):105-108.

Zhai Hongxin,Yang Li,Li Jun.Integral optimization on systematic parameters of flip-flow screens[J].Journal of China Coal Society, 2004,29(1):105-108.

[9] 宁小波,翟宏新,杨汉生.筛面张紧量对弛张筛橡胶筛面动力学参数的影响[J].矿山机械,2009,37(19):107-109.

Ning Xiaobo,Zhai Hongxin,Yang Hansheng.Influence if tensional amount on dynamic parameters of elastomeric sieving plate of flipflow screen[J].Mining&Processing Equipment,2009,37(19): 107-109.

[10] Stanley L Humiston,Andrew T LaVeine.Flexible sieve mat screening apparatus[P].US Patent:US7344032 B2,2008-03-18.

[11] 赵跃民,刘初升,闫俊霞,等.集中驱动式弛张筛[P].中国专利:200810195649.8,2012-01-04.

[12] 董海林,夏云飞,刘初升.弛张筛支撑横梁结构改进对筛面可靠性影响的研究[J].矿山机械,2012,40(2):72-75.

Dong Hailin,Xia Yunfei,Liu Chusheng.Study on impact of structural reconstruction of support beam in flip-flow screen on reliability of screen surface[J].Mining&Processing Equipment,2012, 40(2):72-75.

[13] 吴明德.弹性杆件稳定理论[M].北京:高等教育出版社,1988.

[14] 《数学手册》编写组.数学手册[M].北京:高等教育出版社, 1979.

[15] Lee H J,William E Schiesser.Ordinary and partial differential equation routines in C,C++,Fortran,Java,Maple,and MATLAB [M].Boca Raton:CRC Press,2004.

Analysis and experiment on the large nonlinear deformation of a flip-flow screen

PENG Li-ping1,LIU Chu-sheng1,DONG Hai-lin1,LI Jun1,XIA Yun-fei2

(1.School of Mechatronic Engineering,China University of Mining and Technology,Xuzhou 221116,China;2.China Tobacco Zhengjiang Industrial Co., Ltd.,Hangzhou 310000,China)

In order to study the large nonlinear deformation of the flip-flow screen plane(LNDoFSP),considering the instability of the screen plane under the axial compression force,the dynamic model for a slender compressed bar was adopted.Then,the accurate quantitative assessment on the deformation along the axial length was derived through integration by substitution,and based on which,a numerical algorithm was presented to find that the end of the screen plane should move less than 0.271 5l,where l is the length of the screen plane.Finally,an experimental test was conducted and the results show that the experimental data of the test points mounted symmetrically on either side of the center line of the screen plane are almost the same.Additionally,the errors between the experimental and theoretical data are all less than 7%,which demonstrates that the dynamic model is feasible to describe the LNDoFSP.

the flip-flow screen;the large deformation;the nonlinear deformation

TD452

A

0253-9993(2014)05-0976-05

彭利平,刘初升,董海林,等.弛张筛面大挠度非线性变形分析与实验[J].煤炭学报,2014,39(5):976-980.

10.13225/j.cnki.jccs.2013.0803

Peng Liping,Liu Chusheng,Dong Hailin,et al.Analysis and experiment on the large nonlinear deformation of a flip-flow screen[J].Journal of China Coal Society,2014,39(5):976-980.doi:10.13225/j.cnki.jccs.2013.0803

2013-06-09 责任编辑:许书阁

高等学校博士学科点专项科研基金(博导类)资助项目(20120095110001);中央高校基本科研业务费资助项目(2013DXS03)

彭利平(1987—),男,江苏江阴人,博士研究生。E-mail:plpbeckham@163.com