机器人 CO2 气体保护焊焊缝数学模型研究

林 军，温永策，卢庆亮，曹永华，孙俊生，左增民

1济南重工股份有限公司 山东济南 250109

2山东大学材料科学与工程学院 山东济南 250061

3菏泽广泰耐磨制品股份有限公司 山东菏泽 274600

大型焊接结构件的工程应用日益增多，对厚板的需求也大幅增加。目前针对厚板的焊接常采用的人工焊接方式，焊接生产率较低而且质量稳定性不高，机器人焊接是高效、智能和自动的有效解决方法。实现机器人焊接的首要基础就是提前规划出每一焊道的焊接工艺参数，这就需要建立焊接参数与焊道尺寸的准确数学模型。焊接速度和电流是 2个较为重要的焊接工艺参数。熔高、熔宽和焊道截面积是厚板多层多道焊焊道排布需要重点考虑的 3 个焊道参数。

霍厚志等人[1]根据焊缝体积与填充焊丝体积相等的关系推导出指定焊缝尺寸所需的焊接工艺参数，并通过试验表明预测焊缝尺寸与实际得到的焊缝尺寸相近。徐健宁等人[2]采用二次通用旋转回归设计的试验方法建立了熔深、熔宽、余高与 TIG 焊接参数的回归方程，置信度较高。J.I.Lee 等人[3-4]结合了回归分析和人工神经网络方法，建模分析了焊接电流、电压、速度和坡口间隙对 CO2气体保护焊焊道形状参数的影响。I.Kim 等人[5]使用相同的方法建立了 GMA 焊道熔宽与焊接电压、电流和速度等参数的回归方程。

笔者针对厚板焊接，采用二次通用旋转回归方法设计了单道熔敷焊接试验方案，根据试验得到 CO2气体保护焊焊道余高、熔宽和横截面积与焊接电流和速度的关系，建立了回归方程模型，并对回归方程的拟合性与显著性进行了检验。

1 试验方案

1.1 焊接工艺参数选择

焊接电流、电弧电压、位置、速度、喷嘴高度、板材厚度、是否摆动及摆动幅度是影响 CO2气体保护焊熔敷焊道质量的主要参数。在机器人焊接中，利用变位机使焊接保持在平焊位置。采用 CO2气体保护焊焊接时，焊接电压和喷嘴高度一般均保持不变或变化范围小，通过调整焊接电流和速度来控制熔敷焊道的尺寸。因此，工艺参数变量选择焊接速度和电流，其他参数保持不变。根据 CO2气体保护焊焊接电流及速度的数据[6]，焊接工艺参数如表 1 所列。

表1 焊接工艺参数Tab.1 Welding technical parameters

1.2 焊接试验设计

多因素试验利用正交表或均匀表等进行科学试验设计，通过广义试验寻找最优工艺组合[7]。作为一种现代建模优化方法，回归设计[8]可根据实际情况，进行特性化回归设计。旋转回归设计方法中，距离编码中心不超过 1 的点上预测值方差几近相等，而且预测值方差只与所在点位置有关，试验方案次数少，易于寻找最优方案，因此笔者将利用旋转回归设计方法进行单道熔敷焊接试验方案设计。

焊接试验中工艺参数变量为焊接电流I与速度v，即因子变量个数p＝2。因此，采用二因子二次通用旋转回归设计，每个因素都取-1.414、-1、0、1、1.414，即星号臂长度r=1.414。可得到各因素皆取二水平的全面试验点次数mc=2p=4，各因子在坐标轴上取得试验点(即某个因子的编码值取星号臂长度r，而其他因子的编码值取 0)的次数mr=2p=4，所有因子水平都取 0 水平时进行的重复试验次数m0＝5，总试验点个数n=mc+m0+mr=13。由此可知编码区间：ΔI=(Ir-I-r)/2r=58，Δv=(vr-v-r)/2r=7。利用该方案设计可以得到焊接电流和速度的水平编码，如表 2 所列。其中x1、x2为焊接电流和焊接速度在回归设计中使用的规范水平，实际参数可由其规范水平求得，I=I-r+ΔI(x1+r)，v=v-r+Δv(x2+r)。回归设计试验实施方案如表 3 所列。

表2 焊接电流及速度水平编码Tab.2 Horizontal coding of welding current and velocity

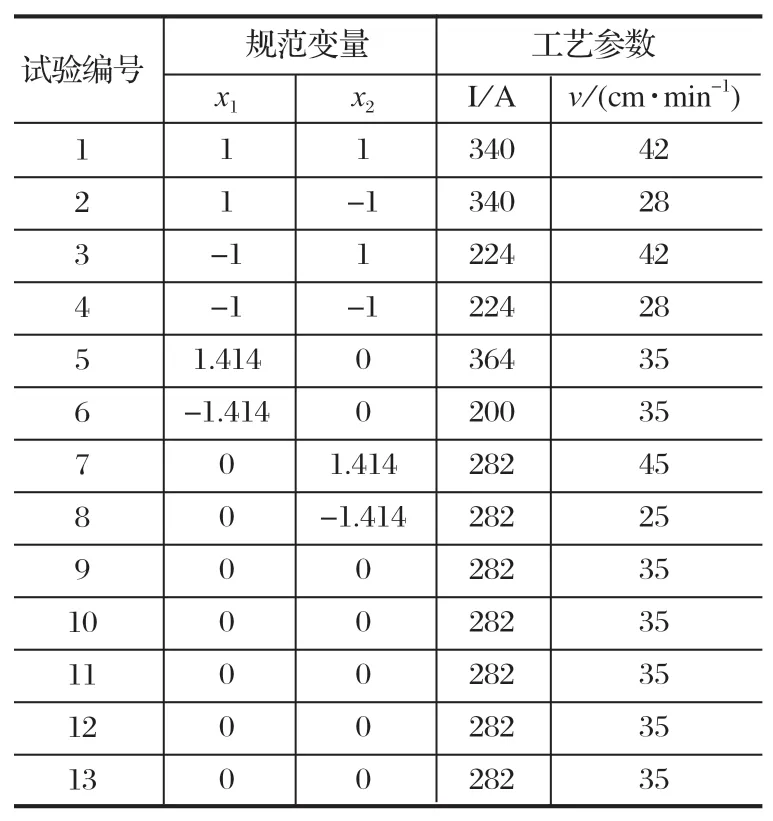
表3 回归设计试验实施方案Tab.3 Implementation scheme of regression design test

1.3 焊接试验

单焊道焊接试验平台如图 1 所示。FANUC 机器人进行 CO2气体保护焊单焊道焊接试验[9]。该试验采用 PulseMIG-500 RPMIG 焊机，焊接电流电压均可单独调控。焊接试板尺寸为 200 mm×60 mm×20 mm，材料为 Q345 钢，焊丝采用 ER50-6，直径为 1.2 mm，采用 CO2气体保护焊，气体流量为 20 L/min。

2 试验结果分析

使用不同焊接参数进行 CO2气体保护焊焊接试验，焊接后试板外观形貌如图 2 所示。

图1 单焊道焊接试验平台Fig.1 Single-pass welding test bench

图2 焊接后试板外观形貌Fig.2 Appearance of welded test plate

为获得准确的焊道尺寸，在焊后试板中段取 3 个位置，沿其截面进行切割并用砂轮和砂纸进行打磨使其平整光亮，利用数码相机拍摄得到焊道横截面宏观照片，如图 3 所示。

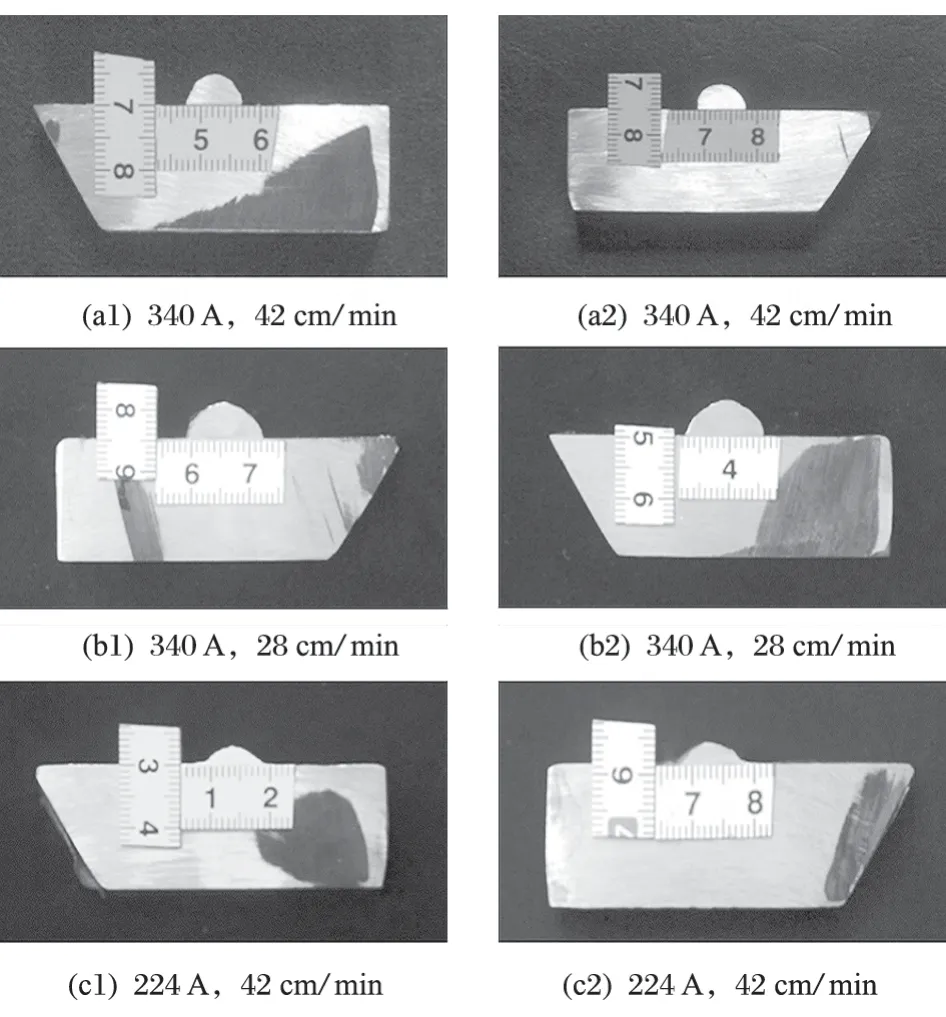
图3 焊缝横截面的宏观相貌Fig.3 Macroscopic appearance of cross section of weld seam

最后在 Image-ProPlus 软件中测得 3 个截面熔宽w、余高h及横截面积S，并取平均值，其结果如表4 所示。从表 4 可以看出，电流增大时，熔宽变化不大，余高和截面积增大。这是因为电流增大后弧柱直径增大，但是电弧潜入工件的深度增大，电弧斑点移动范围受到限制，因而熔宽近于不变，而焊丝融化量成比例地增多，所以余高和截面积增大。当焊接速度增大时，单位长度焊缝上的焊丝金属的熔敷量减少，熔宽和余高均变小。

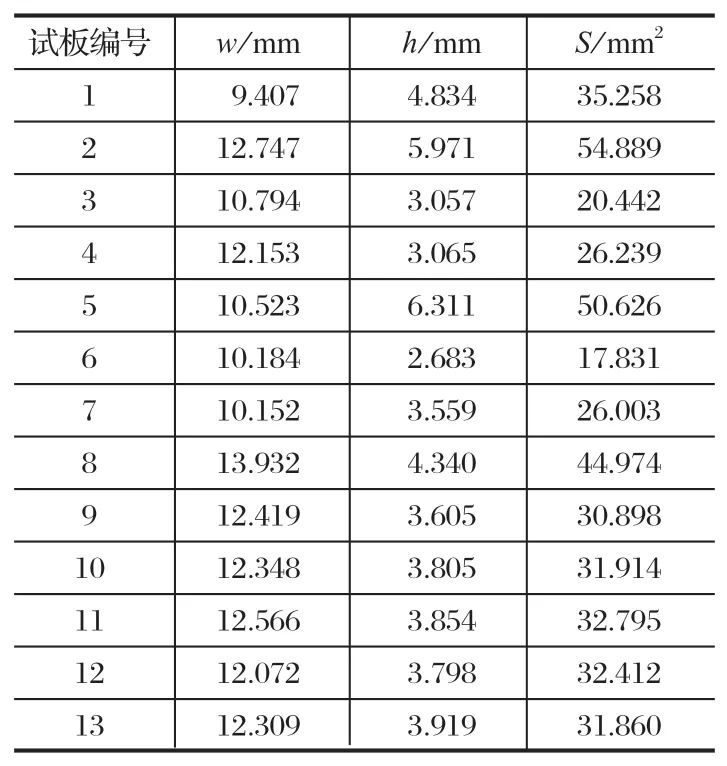
表4 焊道界面数据Tab.4 Dimensions of weld beam interface

3 焊接数学模型

通过数学模型建立焊接工艺参数与焊道尺寸的定量化关系式，可预测焊道熔宽、余高和横截面积，为填满焊缝选择合适的工艺参数。

3.1 回归模型建立

试验中，变量因子个数P=2，因此二次回归模型预测公式为

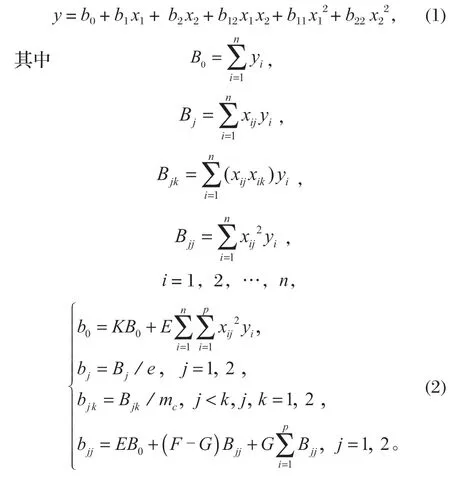
式中：y为预测响应值，即焊道截面参数熔宽w，余高h及截面积S；xj(j=1，2)为自变量即焊接工艺参数焊接速度和电流；b0，bj，bkj(k=1，2)为回归系数；i为试验次数，即为第i次实验所用的工艺参数；K、E、F、G、e根据二次通用旋转组合设计计算参数表[8]选取，得到K=0.2，E=-0.1，F=0.143 8，G=0.018 8，e＝8。

根据上述计算方法及测量数据，建立焊道熔宽w的二次回归方程

3.2 数学模型的检验

虽然建立了焊道熔宽回归方程，但是该方程的拟合效果及其可信程度还不清楚，因此需对回归方程的显著性、拟合性以及回归系数的拟合性进行检验。

回归方程的显著性主要是通过回归方程的置信度以及误差进行检验，通常使用F检验：

式中：SE、SR分别为残差平方和、回归平方和；fR、fR分别为其自由度，fR=2p+p(p-1)/2=5，fE=n-1-5=7。

通过计算得到FR=71.7。一般选择水平a=0.05，根据fR、fE值，通过临界检验表查取临界Fa=(fR、fE)值[8]，得到F0.05(5，7)=3.97＜FR，说明方程在水平a=0.05 是显著的。

上述分析只能说明回归方程在试验参数下拟合效果较好，但在其他参数下的拟合效果也需要进行评估，这就需要进行拟合性检验，

式中：SLf、Se分别为重复试验的误差平方和、失拟平方和，其自由度分别为fe=4 和fLf。笔者在中心点处做了 5 次试验，经计算试验测得熔宽平均值为12.343，误差平方和Se=0.130，自由度fe=m0-1=4，失拟平方和SLf=SE-Se=0.265，自由度fLf=fE-fe=7-4=3，查表文献[8]得到F0.05(3，4)=6.59＜FLf，说明方程在该水平并没有失拟。

此外，为判断各变量因子对回归方程的影响是否显著，还需进行回归系数显著性检验，

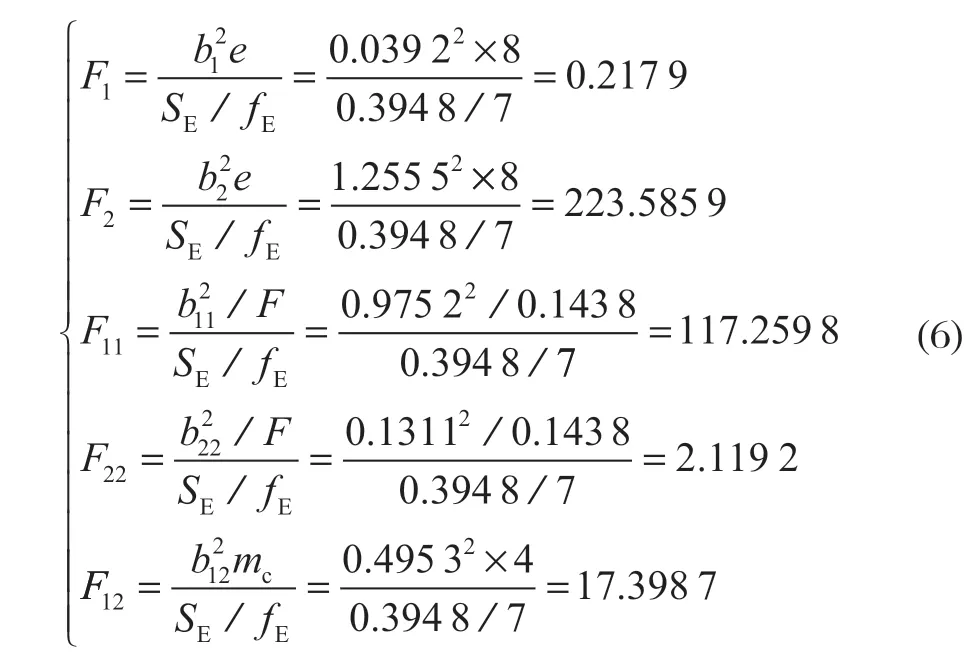
将上式求得的F值与Fa(1，fE)=5.59 进行比较，发现x1与x22不显著。因此剔除回归方程中x1和x22项，得到熔宽的优化回归方程

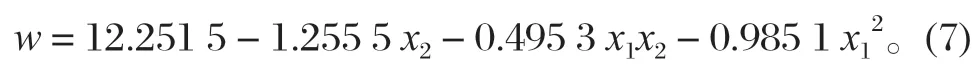
3.3 余高及焊缝横截面积的回归方程

重复式(7)的计算检验方法，可获得余高h和截面积S的回归方程

F检验结果如表 5、6 所列。

由表 5、6 可知，余高回归方程中x22项是不显著的。因此，余高以及横截面积的最终回归模型为

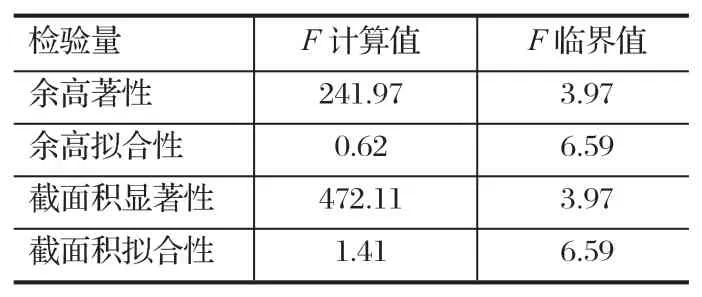
表5 回归方程的显著性、拟合性检验Tab.5 Test for saliency and fitness of regression equation

3.4 回归方程反编码

根据所述二因子二次通用旋转回归设计方法，将编码的变量因子xj(j=1，2)转化为实际工艺参数变量焊接电流和速度。

将其代入式(7)、(10)和式(11)中，最终获得熔宽、余高和横截面积对焊接速度和电流的回归方程

通过式(13)计算得到熔宽、余高和横截面积的预测值，预测值与实测值的对比如表 7 所列。由表 7可知，预测值最大误差仅为 8.4%，与计算得到的回归模型与实测值吻合很好，能够用于焊道截面尺寸的预测。

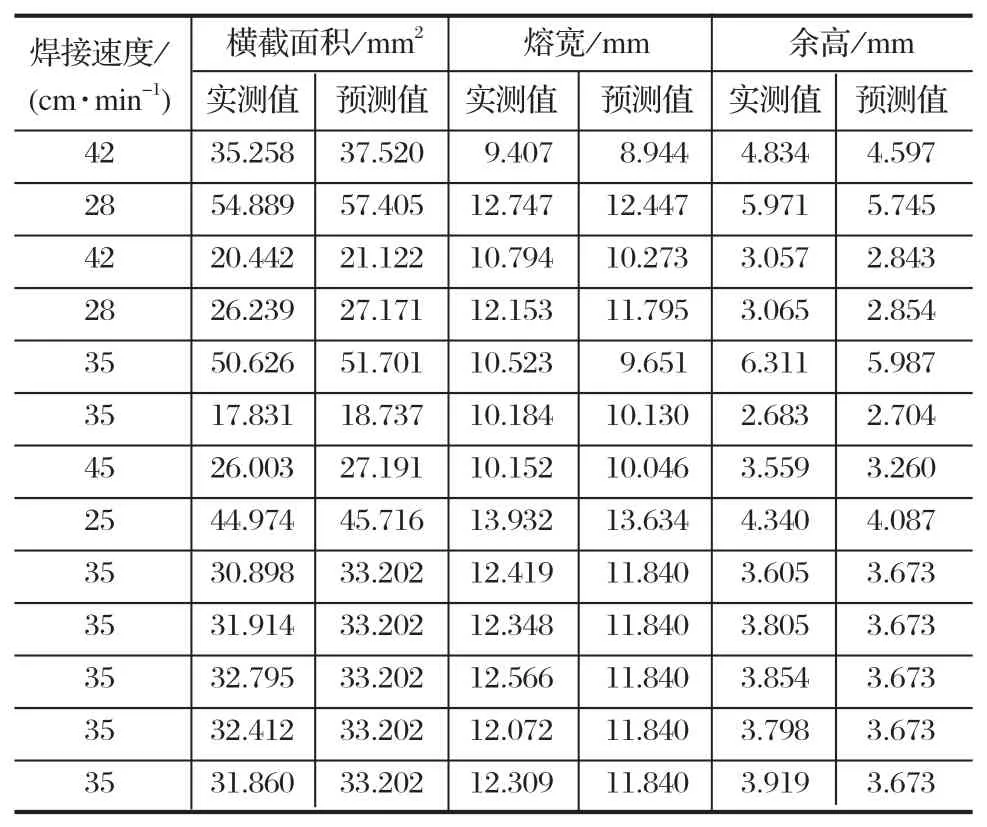
表7 预测值与实测值对比Tab.7 Comparison of predicted and tested values

4 结论

通过采用二次通用旋转回归设计方法进行焊接试验，并使用 Image-ProPlus 处理焊后试样截面照片，获取了焊缝尺寸参数，由此建立了熔敷焊道的余高、熔宽和焊道横截面积关于焊接电流和速度的二次回归方程。对回归方程有效性进行了检验，剔除了不显著项，获得了焊缝成型参数与焊接工艺参数间的回归模型，并与实测值进行了对比，发现回归模型能够很好的预测焊缝截面尺寸，能够用于指导焊接路径规划。