直线振动筛筛面颗粒运动特性分析
2023-11-21李嘉悦
周 扬,屈 阳,严 欣,李嘉悦
(中国矿业大学(北京),北京 100083)
筛分是将颗粒群按颗粒大小进行分离的方法,广泛应用于矿业、农业、建筑行业等领域。提高筛分作业的各项效率,优化筛分设备结构,都需要了解物料在筛分设备上的力学特性和运动状态及透筛规律,筛分过程包括分层和透筛两个过程,筛面上的颗粒运动与筛分设备的结构和工作参数有关。
李云峰[1]等通过理论计算的方法研究了各项参数对筛分效率的影响,陆金新[2]等通过力学分析理论计算了筛分过程中单颗粒的运动特性,为振动筛的动力学优化设计提供理论依据,此理论计算的方法大多不考虑外界干扰的因素,且在计算颗粒运动特性时只计算颗粒刚开始运动的类型从而推测出后续的颗粒运动特性而没有对整个运动过程进行计算。邓嘉鸣[3]等通过实验揭示了振动筛的高效筛分机理与特性,这种方法需要通过大量的实验数据进行统计分析需要耗费大量的时间且每一次实验都会有不同的干扰因素。SHIMOSAKA[4]最早将离散元分析应用于振动筛研究,模拟颗粒群在筛面上的筛分过程,并根据模拟结果得出现象学筛选模型。刘清泉[5]等研究了在筛分过程中煤粒平均粒径对筛分效率的影响,涂晓琴[6]等研究将筛分振幅偏差与筛分振幅偏差变化率对筛分时间、筛分效率、颗粒大小做在线自动整定,实现对振幅的最优控制。DONG[7]等和 JAHANI[8]等基于离散元法模拟了多层香蕉筛分的过程,研究了振动幅度、振动频率、振动方式对筛分过程以及筛分结果的影响。丁振军[9]等通过MATLAB数值模拟与高速摄像技术相结合的方法分析了振动筛筛面运动特性对筛面颗粒受力情况以及颗粒运动状态及形式的影响。Jiangang Yang[10]等在建筑行业基DEM仿真研究了筛面各项参数对筛分效率的影响。直线振动筛结构较大,许多学者对振动筛的某一部件单独分析研究[11,12],ELSKAMP[13]等人对振动筛的振动单元单独分析从而预测了筛分过程中的最佳参数[14],Jinpeng Qiao[15,16]等利用了颗粒运动特性分析了振动筛的筛分效率。
本文将筛板用盲板代替,利用EDEM软件模拟筛面上颗粒运动特性,研究了颗粒沿筛面运动位移与振幅、频率、振动方向角之间的关系模型。通过颗粒与筛面碰撞位置的变化规律,为筛面开孔方式的优化提供技术支撑。
1 研究方法与边界条件
1.1 研究方法
振动筛按照振动轨迹分为圆振动筛和直线振动筛,直线振动筛结构如图1所示,由于直线振动筛结构尺寸较大,为减少模拟计算量,加快计算速度,取振动筛一部分筛面(图1框线部分)进行模拟计算。本文主要研究颗粒在筛面上的运动特性,对直线振动筛结构进行简化,模拟分析时只考虑筛面,如图2所示。为详细研究筛面上颗粒的连续运动特性,防止模拟中途颗粒便已透过筛面,选取颗粒在筛面上连续跳动多次且未透筛的情况进行研究分析,此时颗粒除滑动运动外每次跳动落下时都未通过筛孔仅与筛面实心部分发生碰撞,故以盲板代替筛面进行研究分析,盲板本身存在倾角α,沿振动方向角δ做简谐振动运动。颗粒的运动速度可分解为垂直于筛面的分速度vn以及沿筛面方向的分速度vs,运动轨迹可以分解为沿筛面方向的位移Ss与垂直筛面方向的位移Sn,根据Sn-t的曲线可以得到颗粒与筛面的碰撞时间,而Ss-t曲线反映了颗粒沿筛面方向位移与时间的关系。

图1 ZK型直线振动筛

图2 模拟场景示意
1.2 边界条件
模拟计算采用无滑动接触模型,筛面长度1500 mm,宽度600 mm,筛面材料为钢,煤颗粒直径为10 mm,筛面与物料的物理参数见表1,模拟条件见表2。

表1 筛面与颗粒的物理参数

表2 筛面模拟条件设置
2 筛面颗粒运动特性
颗粒生成后,在重力作用下沿着筛面向下运动,在撞击筛面后被弹起,由于实验条件的不同,颗粒撞击筛面后的运动轨迹也不同。筛面上颗粒的运动类型分为Ⅰ,Ⅱ和Ⅲ,类型Ⅰ表示颗粒与筛面碰撞后无法被弹起主要随筛面做滑动运动,类型Ⅱ表示颗粒的运动过程中既存在滑动运动也存在弹跳运动,类型Ⅲ表示颗粒的运动过程只存在弹跳运动。
2.1 振动方向角对颗粒运动的影响
振动频率为5 Hz、振幅为30 mm、筛面倾角10°的情况下,选取振动方向角20°、30°、50°、70°、80°、90°进行模拟,颗粒的运动轨迹如图3所示,颗粒垂直于筛面的绝对位移曲线如图4所示,绝对位移与筛面本身的位移合成后得到颗粒垂直于筛面的相对位移曲线,如图5所示,Ss随时间变化的关系曲线如图6所示。
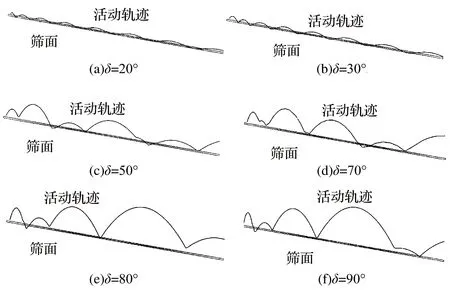
图3 不同振动方向角下颗粒的运动轨迹

图4 不同振动方向角下颗粒垂直于筛面的绝对位移

图5 不同振动方向角下颗粒垂直于筛面的相对位移

图6 不同振动方向角下Ss与时间的关系
2.1.1 对颗粒运动轨迹的影响
由图3可知,改变振动方向角时颗粒的运动轨迹会发生较大的变化。随着振动方向角δ逐渐增大,颗粒与筛面碰撞后垂直于筛面的分速度逐渐增加,颗粒的弹跳高度逐渐增大,颗粒在空中的运动时间增加与筛面接触次数不断减少。δ≤70°时,运动轨迹变化较为明显,δ=80°和δ=90°时,颗粒与筛面第四次接触前的运动轨迹基本相同。
2.1.2 对颗粒碰撞周期的影响
由图4可知,曲线最低点Sn=0,表示颗粒与筛面发生了接触。δ为20°、30°时,颗粒垂直于筛面的绝对位移曲线为一条简谐运动曲线,颗粒与筛面存在多次接触。δ为50°、70°时,颗粒与筛面的接触时间都不相同。δ为80°、90°时,颗粒前四次与筛面的接触时间几乎相同。
由图5可知,Sn减小到零并立刻增大时,表示颗粒与筛面碰撞后被弹起,Sn为零并保持一段时间时,表示颗粒与筛面碰撞后处于滑动运动状态。δ=20°时,颗粒在筛面上一直处于滑动运动状态,δ=30°时,颗粒与筛面碰撞后无法被弹起,只能跟随筛面做滑动运动直到颗粒与筛面在垂直于筛面方向上产生速度差后被再次抛起并以周期T=0.2、振幅A=9.5 mm不断重复,此时颗粒在筛面上只存在滑动运动,这两种情况下的颗粒运动为类型Ⅰ。δ为50°、70°时,颗粒在整个运动过程中同时存在弹跳运动和滑动运动,颗粒运动为类型Ⅱ。δ为80°、90°时颗粒在每次碰撞后都能被弹起且弹跳高度在不断增大,此时颗粒运动为类型Ⅲ。以δ=80°为例,每次碰撞前后颗粒与筛面在垂直于筛面方向上的速度见表3,其中碰撞时筛面的速度为Vsn1、颗粒的速度为Vpn1,碰撞时颗粒与筛面的速度差为ΔV,碰撞后颗粒的速度为Vpn2,颗粒在垂直于筛面方向上获得的能量为E,其中速度的正值表示垂直于筛面向上,负值表示垂直于筛面向下。速度方向相同,颗粒与筛面相向运动,速度方向不同,颗粒与筛面相对运动。从表3数据可以看出,前三次碰撞时颗粒与筛面为相对运动且速度差不断增大,前三次碰撞后颗粒垂直于筛面的最大位移不断增大。从上述分析可以看出,运动类型Ⅰ下的颗粒在筛面上只存在滑动运动,运动类型Ⅱ下的颗粒在筛面上弹跳与滑动并存,颗粒运动为类型Ⅲ时,改变振动方向角颗粒的碰撞周期几乎不会发生变化。

表3 振动方向角80°时碰撞前后颗粒与筛面的速度
2.1.3 对颗粒碰撞间隔的影响
由图6可知,δ≥40°时,随着振动方向角的增大,颗粒与筛面碰撞时沿筛面的分力不断减小,颗粒沿筛面方向上的分速度减慢,颗粒脱离模拟区域的时间增长。取颗粒与筛面碰撞时颗粒沿筛面方向上的位移距离,相邻两次碰撞的位移距离差即为颗粒的碰撞间隔。颗粒运动为类型Ⅰ和Ⅱ时,颗粒在筛面上存在滑动运动,此时颗粒的碰撞间隔无规律可循。δ为80°和90°时,颗粒碰撞间隔的详细数值见表4,其中S(Δn)表示颗粒的第n次碰撞与第n-1次碰撞时沿筛面方向上的碰撞间隔,第0次碰撞记为颗粒在筛面上的初始位置。从表4数据可以看出,随着颗粒的碰撞次数增加,相邻两次碰撞的碰撞间隔在不断增大,而增大振动方向角则会减小颗粒的碰撞间隔。

表4 振动方向角80°、90°时颗粒碰撞间隔
2.2 振幅对颗粒运动的影响
振动频率为5 Hz、筛面倾角为10°、振动方向角80°的情况下,选取振幅为10,20,30,40 mm进行模拟,得到颗粒的运动轨迹、颗粒垂直于筛面的相对位移曲线和颗粒沿筛面的位移随时间变化的关系曲线,分别如图7—图9所示。

图7 不同振幅下颗粒的运动轨迹
2.2.1 对颗粒运动轨迹的影响
由图7可知,随着振幅的增大,筛面的速度不断增大,颗粒与筛面碰撞后获得的速度不断增大,颗粒弹跳的最大高度不断增高,颗粒在空中的运动时间增长与筛面的碰撞次数减少。振幅30 mm时颗粒的弹跳高度已接近阈值,此时再提高振幅并不能明显增大弹跳高度,但会减少颗粒与筛面的碰撞次数,不利于颗粒的筛分。
2.2.2 对颗粒碰撞周期的影响
由图8可知,颗粒在振幅10 mm时的运动为类型Ⅰ,振幅20 mm时的运动为类型Ⅱ,当振幅增大到30,40 mm时颗粒运动为类型Ⅲ。随着振幅的增大,碰撞后颗粒垂直于筛面方向上的速度加快,颗粒垂直于筛面的最大位移不断增大,颗粒在空中的运动时间增长,碰撞周期增大。

图8 不同振幅下颗粒垂直于筛面的相对位移
2.2.3 对颗粒碰撞间隔的影响
由图9可知,随着振幅的增大,筛面速度增大,碰撞后颗粒获得的动能增大,颗粒沿筛面的分速度加快,颗粒脱离模拟区域的时间减短。A=30,40 mm时,颗粒碰撞间隔的详细数值见表5。从表5数据可以看出,随着振幅增大,颗粒的碰撞间隔不断增大。

表5 不同振幅下颗粒的碰撞间隔
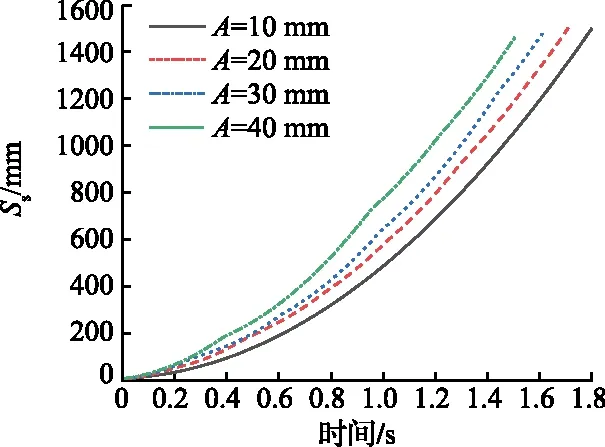
图9 不同振幅下Ss与时间的关系
2.3 频率对颗粒运动的影响
筛面倾角为10°、振动方向角为80°、振幅为30 mm的情况下,选取振动频率为3、4、5、6、7 Hz进行模拟,得到颗粒的运动轨迹、颗粒垂直于筛面的相对位移曲线和颗粒沿筛面的位移随时间变化的关系曲线,分别如图10—图12所示。

图10 不同频率下颗粒的运动轨迹
2.3.1 对颗粒运动轨迹的影响
从图10可以看出,随着频率增加,筛面速度不断增大,颗粒与筛面碰撞后获得的速度和颗粒弹跳高度不断增大。3≤f≤5 Hz时,增大频率颗粒的运动轨迹变化较为明显。5≤f≤7 Hz时,增大频率虽然仍会影响颗粒的运动轨迹,但颗粒的最大弹跳高度基本相同。
2.3.2 对颗粒碰撞周期的影响
由图11可知,频率3 Hz时颗粒运动为类型Ⅰ,频率4~7 Hz间的颗粒运动为类型Ⅲ。随着频率的增大,筛面速度不断增大,碰撞后颗粒垂直筛面的分速度增大,颗粒在空中的运动时间不断增长,垂直于筛面的最大位移不断增大,碰撞周期不断增大。f=6 Hz时,颗粒垂直于筛面的最大位移可达到450 mm,此时再增大频率,颗粒在空中的运动时间过长,颗粒与筛面无法保证每次碰撞时都处于相对运动状态,颗粒垂直于筛面的最大位移反而会降低。当频率从6 Hz增大到7 Hz时,从第二次碰撞开始颗粒垂直于筛面的最大位移会降低,同时颗粒的碰撞周期也会减小。

图11 不同频率下颗粒垂直于筛面的相对位移
2.3.3 对颗粒碰撞间隔的影响
由图12可知,3≤f≤6 Hz时,随着频率的增大,筛面速度增大,碰撞后颗粒沿筛面的分速度增大,颗粒脱离模拟区域的时间减短。f=7 Hz时,颗粒脱离模拟区域的时间大于f=6 Hz时的时间。f为4,5,6,7 Hz时,颗粒的碰撞间隔数据见表6。从表6数据可以看出,随着频率增大,颗粒的碰撞间隔先增大后减小,在6 Hz时达到最大。

表6 不同频率下颗粒的碰撞间隔

图12 不同频率下Ss与时间的关系
3 结 论
1)改变条件会影响颗粒的运动过程,产生三种运动类型,运动类型Ⅰ和Ⅱ下的颗粒在筛面上存在滑动运动,运动类型Ⅲ下的颗粒不存在滑动运动。
2)颗粒运动为类型Ⅲ时,改变振动方向角不会影响颗粒的碰撞周期,增大振动方向角会减小颗粒的碰撞间隔。
3)颗粒运动为类型Ⅲ时,颗粒的碰撞周期和碰撞间隔随着振幅的增大而增大,随着频率的增大先增大后减小。
4)增大振动方向角、频率和振幅都会减少颗粒与筛面的碰撞次数。
5)当颗粒运动为类型Ⅲ时,大多数模拟情况下,随着颗粒的碰撞次数增加,颗粒的碰撞间隔会不断增大,颗粒在筛面的最初的几次碰撞落点较为密集,是优良的筛分区域,筛面开孔时应在落点密集的区域增大开孔率。考虑到盲板与实际带有筛孔的筛面在碰撞落点有一定区别,在筛面开孔时可结合模拟结果和实际生产经验来指导优化开孔方式。
