一种基于几何特征由粗到细点云配准算法
2020-04-24胡加涛吴晓红何小海王正勇
胡加涛, 吴晓红*, 何小海, 王正勇, 龚 剑
(1.四川大学电子信息学院,成都 610065; 2.成都西图科技有限公司,成都 610021)
点云配准是三维计算机视觉中的一个基本问题。通常采用激光扫描仪获取点云,由于光在物体表面不能穿透,物体表面的信息往往需要多视角、多分辨率扫描获得。给定不同坐标系下的几组点云,配准的目的是找到将它们对齐到最佳公共坐标系的变换。通常需要对多个视角的点云进行配准才能获取完整的信息,其中最基本的是两个视角点云配准。点云配准在许多视觉应用中发挥着重要作用,例如三维重建[1]、机器人视觉[2]、医学研究[3]、文物数字化[4]等领域。
点云配准最经典的算法是由Besl等[5]提出的迭代最近点( iterative closest points, ICP)算法,该算法简单易理解,但配准效果受初始位姿影响较大,每次迭代都要搜索最近点,且没有包含局部特征信息。因此,中外学者提出许多改进的方法。为了避免局部最小值,Yang等[6]将ICP算法和分支定界(branch and bound, BnB)算法相结合,有效地搜索旋转和平移空间,保证全局最优,但计算量大,难以用于数据量大的场合;针对ICP算法迭代速度慢的问题,Han等[7]将分层搜索方案与基于八叉树的ICP算法相结合,有效提高配准效率;Yang等[8]基于统计特性提出局部特征统计描述符(local feature statistics histogra,LFSH),通过编码局部深度、点密度和法线之间的角度的统计特性,形成局部形状几何的全面描述,获得更稳健的匹配点对;Lin等[9]等将点云转换成2D方位角图像,然后使用基于2D特征的匹配方法(speeded up robust features,SURF)来寻找两幅图像之间的匹配像素对,该方法对两场景的相似性要求较高,不适合视角变化大的场景。上述算法大多忽略了点云的几何特征。
针对ICP算法对初始位置敏感且收敛速度慢的问题,提出基于几何特征由粗到细点云配准算法。粗配准阶段,采用基于曲率特征4点匹配,为细配准提供良好初始位姿;细配准利用法向量夹角启发最近点的搜索,加快ICP迭代速度。
1 基于曲率特征4点匹配的粗配准
邻域曲率作为鲁棒且计算快速的局部特征描述子,具有刚性变换不变特性。利用曲率特征进行粗配准。首先寻找点云的最佳投影平面,将点云投影到平面上,然后在平面上提取4个轮廓点,再根据投影变换寻找轮廓点的三维对应点,计算三维点邻域内的各点的曲率,根据曲率变化率的最值寻找特征点,匹配特征点得到初始变换参数。
1.1 曲率特征提取
表面曲率是描述三维曲面局部变化的一个重要度量,通过二次曲面拟合点p的k个最近邻点来估计点p的曲率,将曲面定义为
f(x,y)=a0x2+a1y2+a2xy+a3x+a4y+a5
(1)
利用最小二乘法来估计曲面的参数a0、a1、a2、a3、a4、a5,然后利用差分几何计算高斯曲率K和平均曲率H。

(2)
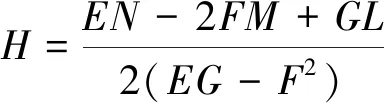
(3)
式中:E=rxrx;F=rxry;L=rxxn;M=rxyn;E=rxrx;G=ryry;rx、ry、rxx、ryy、rxy是二次曲面的偏导数。
主曲率k1和k2通过高斯曲率和平均曲率计算得到。
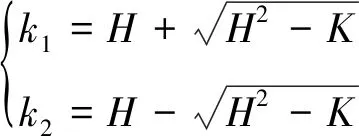
(4)
式(4)中:k1是最大主曲率;k2是最小主曲率。
Chen等[10]研究表明,特征点是邻域中曲率形状变化最大的点。根据这一特点,利用式(5)计算局部曲率变化率C(p),即

(5)
对于邻域中某点pi若满足:
C(pi)>max[C(pi1),C(pi2),…,C(pik)]
(6)
则点pi为邻域凸点;若满足:
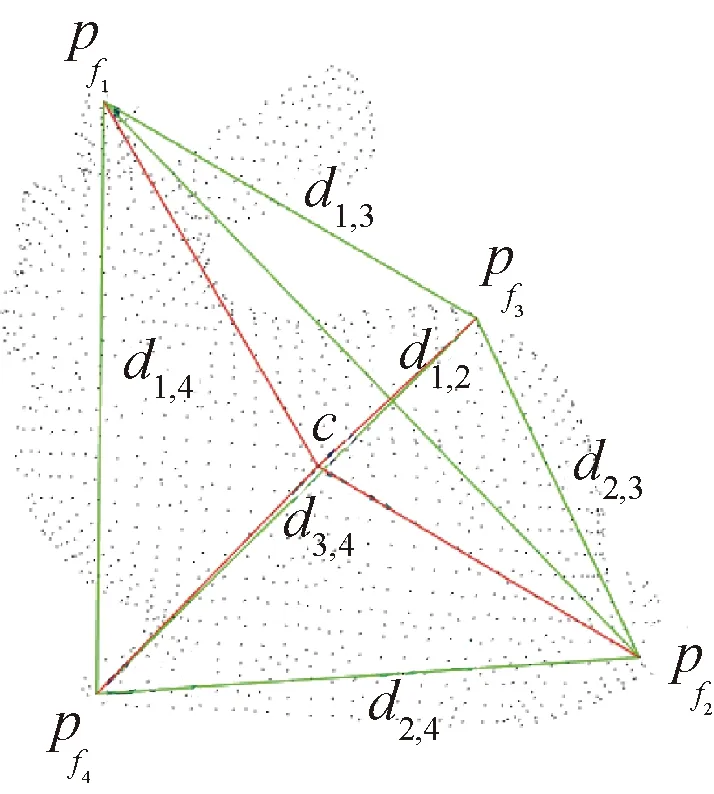
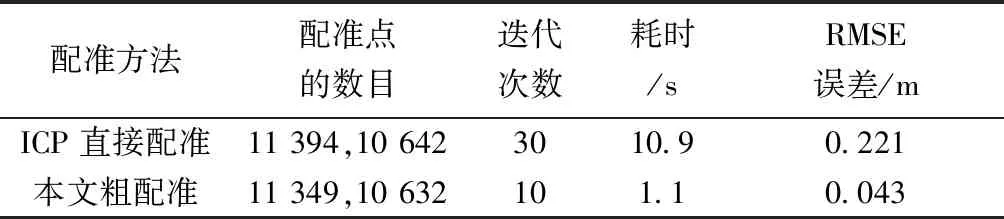
C(pi) (7) 则点pi为邻域凹点。 式中:C(pi1)、C(pi2)、C(pik)为pi点局部曲率形状描述C(p)值。 通常,点云数据量很大,若直接计算所有点的曲率形状特征,效率低。一般有两种方法来处理源数据:一种是通过创建体素网格,用网格的重心点来代表这些点,并且用所有的重心点作为特征点;另一种办法是选取点云最有代表性的特征点。4点全等集算法[11](4-points congruent sets,4PCS)利用共面4点的仿射不变性进行点云配准,受此启发,通过选取不在一个平面的4点来粗略定位点云在空间中的大小和轮廓。在此基础上提出基于投影的最大距离轮廓特征点提取算法。 (8) 在平面上选取的4个点如下: 第1个点f1为距离中心点最远的点,为 (9) 第2个点f2为距离f1点和中心点最远的点,为 (10) 点f1到中心点c的直线和点f2到中心点c的直线形成了以中心点c为顶点的∠f1cf2。 第3个点f3在∠f1cf2的角平分线上,并为距离中心点c最远的点。 第4个点f4在以f3为定点的射线f3c上,并为距离中心点c最远的点。 找到这4个点之后,将这4点映射到三维空间中,分别为p1、p2、p3和p4,pi∈S,然后在这4个点周围选取k个最近邻点,根据式(5)计算k个点的曲率形状变化率C(p),根据式(6)和式(7)寻找这4个点邻域内的特征凹点或特征凸点作为特征点,将4个特征点记为pf1、pf2、pf3和pf4,其中pfi∈S′∈S,点之间的距离为d1,2、d1,3、d1,4、d2,3、d2,4、d3,4,如图1所示,其中di,j表示点pfi与pfj之间的距离。 图1 特征点及特征点之间的距离Fig.1 Feature point and distance between feature points 根据式(11)计算两个4点集匹配的相似度。 (11) 参考文献[12],初始变换矩阵Tr可以通过公式计算: Tr=[P(c)p(t)T][P(t)p(t)T]-1 (12) 式(12)中:P(c)和P(t)为源点云和目标点云的4个轮廓特征点组成的特征矩阵。其中P(τ)定义如下: (13) 当τ=c时,为源点云特征点矩阵;当τ=t时,为目标点云特征点矩阵,p(c)和P(t)的每一列中的(x,y,z)三维坐标点都是一对匹配的轮廓特征点。 粗配准后源点云和目标点云部分重合,此时细配准进一步减少两点云的均方根误差。细配准采用法向量作为点云特征匹配的度量。通过法向量夹角来启发搜索以改善点云配准速度,同时避免陷入局部最小值。 (14) 利用奇异值分解(singular value decomposition,SVD)或者非线性优化计算得到刚性变换矩阵,并更新目标点云的位置,多次迭代,直到收敛于给定的阈值时停止。 通过法向量及法向量夹角,使得搜索时利用法向量方向的相似性确定性向一个方向接近最近点,以改善传统ICP迭代次数过多的问题。 2.2.1 法向量及法向量夹角 利用点云库[13](point cloud library,PCL)很容易计算点的法向量。法向量夹角可以衡量物体表面局部区域变化趋势,若点pj及其邻域内一点pi处的法向量分别为nj和ni,则法向量夹角为 (15) 若θ≤5°,则认为这两个向量具有相同变化趋势,为了计算方便,取cos(θi,j)。 2.2.2 ICP启发式搜索 传统ICP 根据距离,在k邻域内逐个点搜索,有时收敛到错误的位置。启发式搜索允许根据法向量夹角的相似性选择更有效的搜索路径,使ICP算法收敛更快。粗配准基础上,取源点云和目标点云最近点作为一组粗略匹配点为(pi,qj),其中pi∈S,qj∈T。给定刚体变换初值s0=[R0,t0]T,R0为初始旋转矩阵,t0是初始平移矩阵,迭代次数num=0。此时使用启发式搜索进一步优化R0和t0,如下。 输入:给定源点云与目标点云的一组粗匹配及收敛阈值ε。 输出:最优旋转和平移矩阵。 (1)从源点云S中选择点pi,并计算邻域法向量nsi。 (2)从目标点云T中选择pi的粗匹配点qj的k个最近点,并计算这些点的法向量nqj。 (3)将nsi与目标点邻域内k个最近点的法向量nqj进行匹配,利用式(15)计算pi与qj邻域各点法向量夹角,并把具有相同变化趋势的法向量的点对构成对应点集合m(pi,qj)。 (4)从对应点集合中选取法向量夹角最小的一组对应点(pi,qx),用奇异值分解(SVD)计算旋转矩阵Rk+1和平移矩阵tk+1,则sk+1=[Rk+1,tk+1]T,并更新目标点云的位置。 (5)计算两点云的均方根误差(root mean square error,RMSE),若RMSEk+1 (6)若出现RMSEk+1>RMSEk,选取法向量夹角较大的一组点(pi,qx),继续步骤(4)。 (7)若多次出现RMSEk+1>RMSEk,则减小k,继续迭代,直到收敛。 实验平台为Intel(R) Core(TM) i5-7500 CPU@3.4 GHz 64位8 G内存的计算机,软件平台为VS2013,结合PCL点云库实现算法。实验数据来源于三维公园开放的三维扫描数据,数据本身噪点少且模型比较完整,选取其中雕塑、汽车和鞋子点云模型,其中汽车模型在结构上具有对称性,可以验证算法对对称结构的鲁棒性。由于待配准两点云数据不是一一对应关系,业内还没有统一的标准来衡量点云配准精度,通常用均方根误差RMSE来衡量精度。在对比算法效率时,记录各算法在相同收敛阈值条件下,多次迭代所需总的物理运行时间。 首先验证初始位置对ICP算法的影响和本文粗配准结果,如图2所示。实验中ICP算法直接从初始位置开始迭代配准,由于初始位置较远及旋转角度较大,迭代30次后陷入局部最小值,配准后的结果图RMSE误差最小,但继续迭代后,误差变大且配准结果偏差增大。表1中配准点的数目是源点云和目标点云下采样后参与配准的点数。图 2(c)所示是本文粗配准的结果图,此时两点云部分重合,需细配准进一步配准以减小RMSE值。 图2 ICP配准和本文粗配准结果Fig.2 ICP registration and coarse registration results 表1 ICP直接配准和本文粗配准结果 图2、表1的结果表明,若两点云初始位置较远且旋转角度较大时,ICP算法需要多次迭代,最终可能陷入局部最小值,而所提出的基于曲率特征4点匹配的粗配准能将两点云快速拉近,并且不需要多次迭代计算,为细配准提供良好的初始位置。 在粗配准的基础上,细配准对比算法包括经典ICP算法、基于协方差矩阵改进的GICP[14]算法和迭代全局相似点的GH-ICP[15]算法。测试时,先使用理想点云模型进行实验,图3、图4是没有添加噪声的实验结果,然后分别在源点云和目标点云中添加高斯噪声,模拟外部设备获取点云时离群点较多或者环境噪点较大的情形,测试算法对噪声的鲁棒性,结果如图5、图6所示,表2所示是实验数据对比。 图3 无噪声时shoe模型的配准结果Fig.3 Registration result of shoe model without noise 图4 无噪声时对称car模型的配准结果 Fig.4 Registration result of symmetric car model without noise 图5 添加高斯噪声后在shoe模型上的结果Fig.5 Results on the shoe model after adding Gaussian noise 图6 添加高斯噪声后在对称的car模型上的配准结果Fig.6 Registration results on a symmetric car model adding gaussian noise 表2 配准算法结果 从图3、图5可以看出,各算法对于鞋子模型这类非对称结构具有较好配准效果,而对于图4、图6这种对称结构来说,配准效果受到影响,并且有噪声时,这种差异性表现更明显。从表2可以看出,经典ICP算法往往需要多次迭代,配准精度不高,且易受噪声和对称结构的影响。GICP和GHICP算法迭代次数相比ICP有所减少,4种算法中GHICP算法在配准精度表现最好,但需要复杂的计算,耗时较多。而本文提出的基于法向量和法向量夹角的点云精细配准算法通过法向量夹角启发搜索匹配点,加速了点云的收敛,在保证配准精度的同时,减少迭代次数,耗时少,且对于对称结构具有良好的鲁棒性,并且对具有噪声的点云也有较好的配准效果。 粗配准通过投影和映射寻找三维空间各4个轮廓特征点,利用特征点的曲率和特征点之间的距离寻找两点云特征点的最佳匹配,最终得到初始变换参数;细配准阶段,以法向量为特征寻找最近点,通过法向量夹角启发最近点搜索,快速寻找到最优的匹配点,加快ICP的迭代速度。最后,选取了具有代表性的点云模型进行了实验,得出如下结论。 (1)提出的基于曲率特征4点匹配的粗配准能使距离较远、旋转角度较大的两点云快速靠拢,为细配准提供良好的初始位置,避免陷入局部最小值。 (2)在细配准中,本文算法对比其他3种算法,在保障配准精度的同时,在迭代次数和配准速度上更具优势且鲁棒性强,与传统ICP算法相比配准误差减少59.15%,迭代耗时减少46.01%。 今后考虑有效融合物体表面的颜色纹理特征,提高点特征匹配的精确性,从而提升搜索匹配点的正确率,最终提高配准的速度。1.2 最大距离的轮廓特征点提取
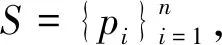
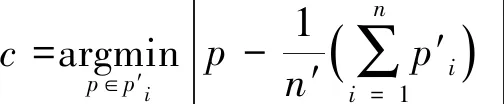
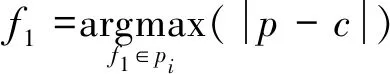
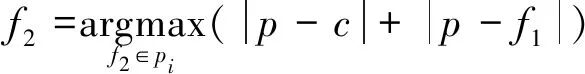
1.3 基于相似度的4点粗配准



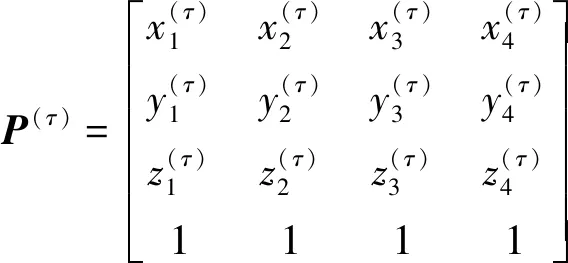
2 法向量启发搜索的点云细配准
2.1 传统ICP算法

2.2 本文算法
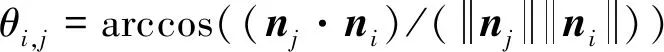
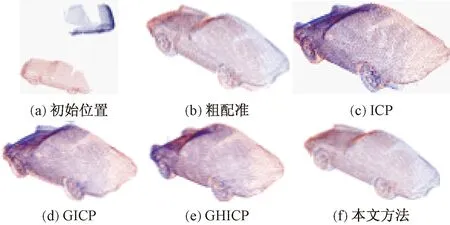
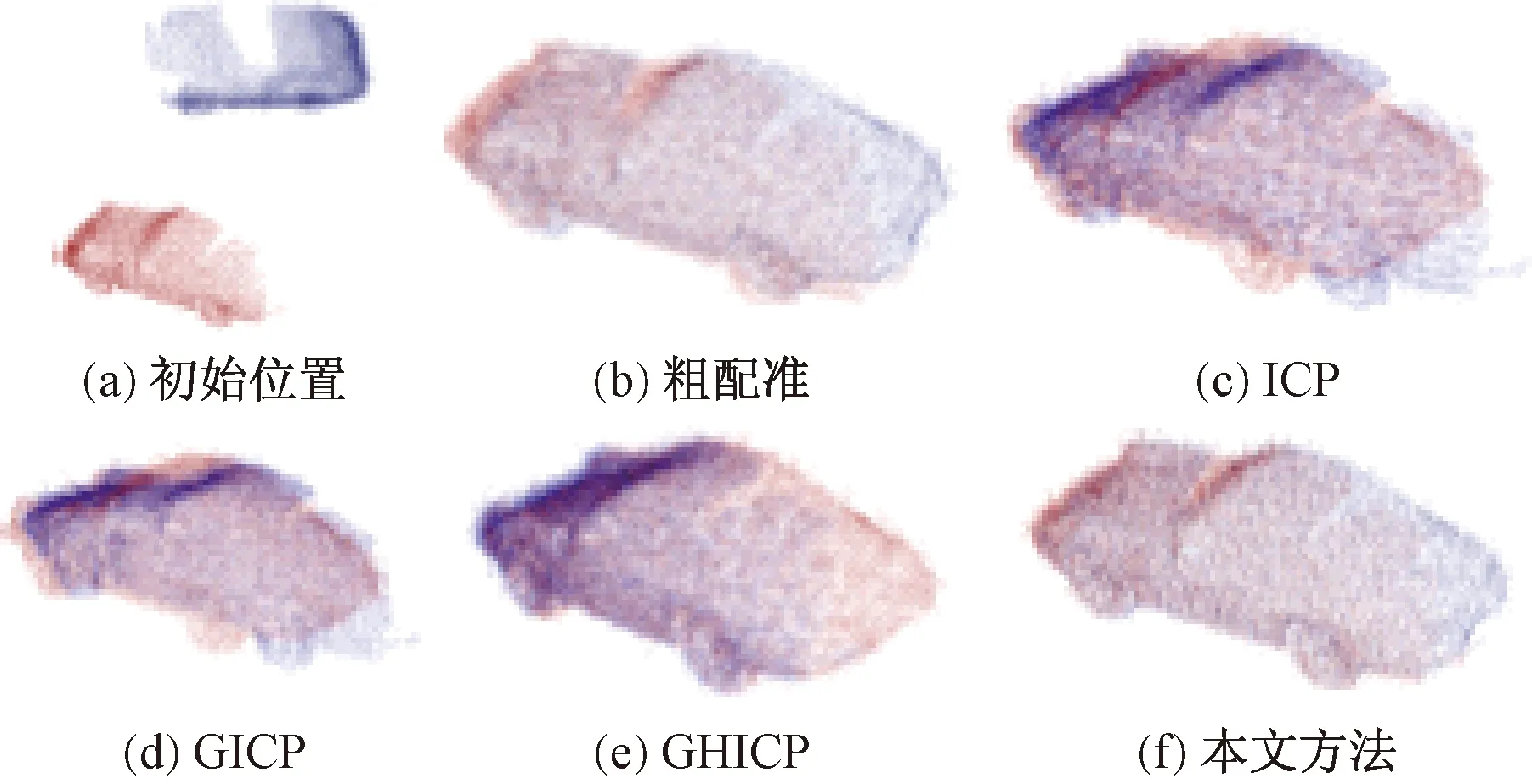
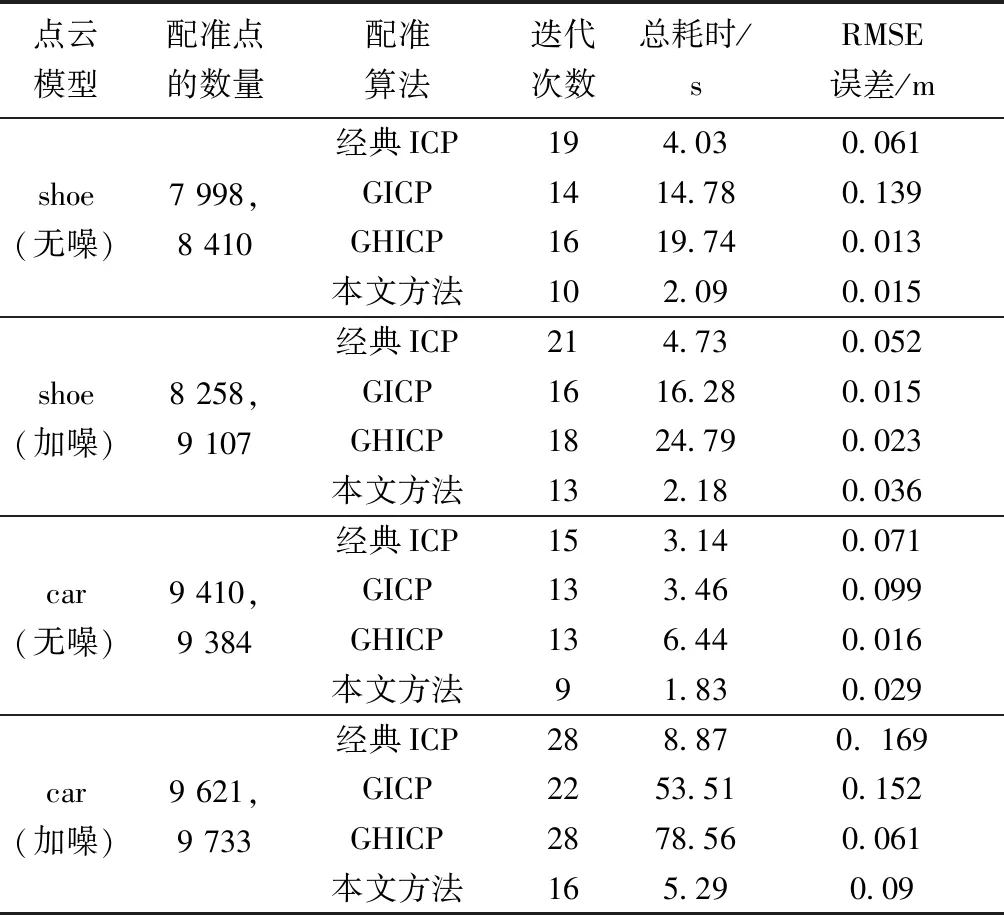
3 实验及结果分析



4 结论
