瓦斯爆炸对巷道壁面损伤破坏的数值模拟研究
2020-04-24邓照玉
邓照玉
(1.中煤科工集团重庆研究院有限公司,重庆 400037;2.国家煤矿安全技术工程研究中心,重庆 400037)
瓦斯爆炸事故是煤矿生产过程中严重的灾害之一,会造成巨大财产损失和人员伤亡。研究瓦斯爆炸的传播规律和爆炸过程中的破坏规律将有利于制定相应防爆抑爆措施,减少瓦斯爆炸对巷道的损伤。
目前中外学者已经对瓦斯爆炸的传播过程进行了大量的理论分析、数值模拟和试验研究,例如,Li等[1]计算了不同爆炸载荷作用下的混凝土分段柱数值结果,与整体柱相比节段间的滑移和开孔能有效吸收爆炸能量,从而减少了爆炸引起的混凝土的损伤破坏;Zhan等[2]通过现场试验和数值模拟,研究了在瓦斯爆炸作用下加固黏土墙体的性能,发现随着墙体厚度的增加和高度的降低,墙体的最大位移和损伤水平显著降低;Wang等[3]通过试验和数值模拟相结合的方法研究了瓦斯爆炸过程及破坏效果,分析了建筑物内爆炸冲击波的传播过程,计算结果表明,超压场和温度场变化情况相一致;林柏泉等[4]在数值计算和模拟实验基础上,研究了瓦斯爆炸过程中火焰传播规律,发现障碍物的存在能够促使爆炸冲击波火焰传播速度;江丙友等[5]发现了可以用二次抛物线方程来表达爆炸传播距离与对应时间之间的关系,据此可估算出巷道各处火焰传播速度大小。陈国华等[6]基于任意的拉格朗日-欧拉(arbitrary Lagrange-Euller,ALE)算法与流固耦合,建立了密闭空间燃气爆炸数值模型,探究了燃气爆炸过程冲击波的传播变化规律,得到了冲击波变化规律,据此拟合了冲击波传播衰减计算公式;张宇等[7]研究了爆炸作用下地下岩土结构界面反射机理,探讨了不同结构和尺寸下的反射系数,得出了爆炸位置、介质参数和结构参数对界面反射都有不同程度的影响。张秀华等[8]分析了在室内的燃气爆炸冲击波的特性及对结构的作用,得出混合气体化学配合比达到最佳比例时,产生的爆炸载荷冲击波峰值压力最大,对结构产生的破坏作用最大;孔德森等[9]建立了地铁隧道的爆炸计算模型,地铁隧道在爆炸载荷作用下的计算与分析可知,壁面的速度和加速度变化与冲击波的超压相关。滑帅等[10]基于流体动力学软件FLUENT 在不同拐角的巷道内对9.5%浓度的瓦斯爆炸气体进行了数值模拟研究,得出瓦斯爆炸在拐角巷道会产生较为复杂的流场,爆炸冲击波的速度、压力和温度等参数在传播过程中会逐渐增加;杨旭等[11]利用ANSYS/LS-DYNA有限元软件,研究了圆形拼装桥墩在爆炸冲击波作用下的动态响应与损伤,得出增加初始预应力可以减少其侧向位移,从而提高抗爆能力;田力等[12]对爆炸载荷作用下的框架结构的连续倒塌机理进行了分析,对比了不同条件下的破坏过程和倒塌程度,得出结构内力重分配使相邻结构损伤,爆源所在不同的位置其破坏范围有显著的区别;彭佳等[13]研究了一种柔性防护结构用于减缓爆炸冲击波破坏作用,得出柔性结构能有效地减少冲击波峰值,对结构防护结构设计具有重要的参考价值。多数学者的研究主要集中在爆炸载荷作用下的动力响应,而很少有研究瓦斯爆炸作用下对壁面结构的损伤破坏过程。
与其他爆炸相比,巷道内瓦斯爆炸是在密闭的受限空间内,且巷道内条件复杂多变。目前对于瓦斯爆炸对壁面结构损伤破坏的研究较少,尤其在数值模拟研究方面,缺乏系统研究,为了进一步研究巷道内瓦斯爆炸损伤过程,建立了巷道瓦斯爆炸物理模型和数学模型,运用ANSYS/LS-DYNA软件的非线性动力分析方法,以典型巷道结构模型为研究对象,通过对封闭端面和轴向壁面结构破坏过程的分析,比较直观地得到了壁面损伤的过程,展示了不同时间下的爆炸超压变化和壁面云图变化。巷道内瓦斯爆炸冲击波传播规律及破坏特性的数值模拟研究,揭示了瓦斯爆炸对巷道壁面损伤的规律,从而为巷道结构的加固设计及制定抗爆抑爆的措施提供理论依据。
1 瓦斯爆炸计算模型的建立
1.1 数学模型
1.1.1 基本假设
瓦斯爆炸是一种极其复杂的物理化学反应,涉及大量的瞬间和中间产物,为了简化计算,忽略爆炸过程的中间产物,瓦斯爆炸过程是不可逆反应,巷道内瓦斯混合气体比热容遵循混合规则,掘进巷道内只有瓦斯爆炸热源存在且不考虑巷道内与外界的热交换,巷道模型壁面视为刚性壁面,巷道空间为标准大气压条件,瓦斯初始状态温度和压力均匀分布。
1.1.2 基本控制方程
在掘进巷道瓦斯爆炸中,是一端封闭,一端开口的受限空间内爆炸冲击波的流动过程。在直角坐标系中,满足质量守恒定律、能量守恒定律、动量守恒定律、状态方程。瓦斯爆炸过程中三维流动的守恒方程如下。
质量守恒方程:
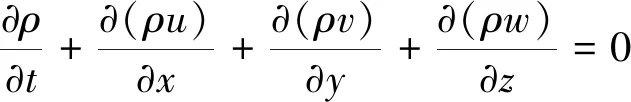
(1)
动量守恒方程:
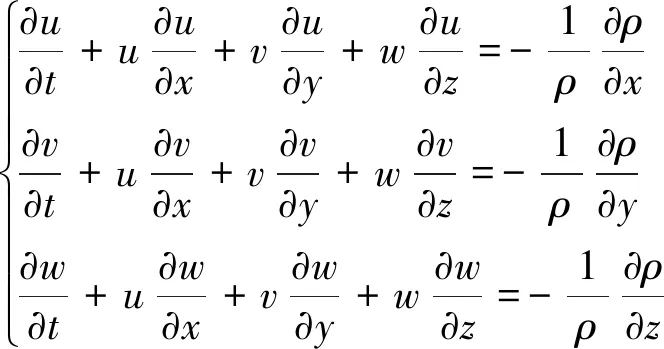
(2)
能量守恒方程:
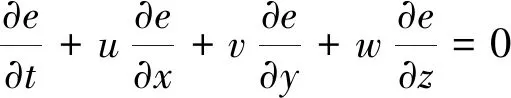
(3)
状态方程:
p=p(ρ,T)=ρRT
(4)

1.2 物理模型
1.2.1 有限元模型的建立
ANSYS/LS-DYNA中ALE建模方法可以实现爆炸冲击波对巷道壁面的损伤破坏的模拟分析。因此,瓦斯气体、空气及巷道均采用3D SOLID 164实体单元建模,在ANSYS/LS-DYNA包含的显示动力单元类型为线性单元,能够很好地运用在大变形和材料失效的问题上。物理模型如图1所示。
根据模型的对称性,建立1/2掘进巷道瓦斯爆炸模型进行分析,构建“瓦斯-空气-巷道壁面结构”的流固耦合数值模型。有限元模型如图2所示。爆源位置位于巷道前端,模型尺寸为10 m×2 m×1 m(长×宽×高),巷道壁面厚度为0.2 m,掘进巷道为一端开口,一端封闭的结构,其中瓦斯与空气预混气体用薄膜隔开,巷道边界条件为无反射边界以模拟无限域。

图1 巷道物理模型Fig.1 Roadway physical model

图2 有限元模型Fig.2 Finite element model
1.2.2 材料参数的选择与状态方程
P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+
C6μ2)ρ0E
(1)
式(1)中:μ=ρ/ρ0-1;C0~C6为状态方程参数,为定义常数;ρ为当前密度,kg/m3;ρ0为初始密度,kg/m3,ρ/ρ0为相对密度;E为材料的内能。空气计算参数如表1所示。
模拟中爆炸模型采用*MAT_HIGH_EXPLOSIVE_BURNJWL,状态方程为*EOS_JWL(Jones-Wilkins-Lee),状态方程的p-V关系如下:
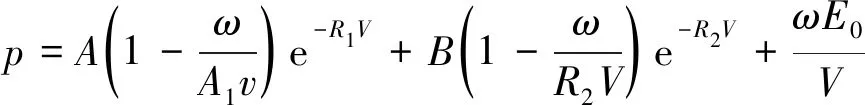
(2)
式(2)中:p为爆轰压力,Pa;V为相对体积,m3;E0为初始内能密度,kJ/m3;参数A、B、R1、R2和ω为爆轰实验确定的材料常数。巷道壁面在瓦斯爆炸冲击波作用下,会出现壁面损伤破坏演化和裂痕扩展,在表面产生拉伸应力,导致壁面拉伸破坏。因此壁面结构采用H-J-C(Holmquist-Johnson-Cook)模型,巷道壁面参数如表2所示[14-16]。

表1 空气计算参数

表2 巷道壁面参数
注:ρc为巷道壁面的密度;Ec为弹性模量;vc为泊松比;Gc为剪切模量;K、m、KIC为壁面性能参数;σcy为抗压强度;fs为壁面失效应变;fd为损伤度值。
2 数值模拟与结果分析
2.1 壁面超压分析
2.1.1 封闭端壁面超压分析
为保证SBS改性沥青混合料拌和稳定性,本项目选用间歇式拌和机进行沥青混合料的拌和,由于SBS改性沥青黏度较普通基质沥青高,因此在拌和SBS改性沥青混合料时,一般会增加5~10s的拌和时间,以确保SBS改性沥青能够均匀裹覆在集料上。另一方面,由于SBS改性沥青所需的拌和温度较高,因此在实际施工过程中应严格控制沥青混合料的拌和温度,既要避免温度过低影响路面铺筑质量,另一方面还要防止温度过高引起沥青混合料老化。
在掘进巷道封闭端壁面选取一系列目标点来记录爆炸冲击波破坏过程的参数变化,如图3所示,巷道内部沿高度方向(X轴)每隔0.2 m选取一个采集点,共选择5个采集点。巷道侧面长度方向(Y轴)每隔0.2 m选取一个数据采集点,共9个数据采集点。不同时刻下各测点超压时程曲线如图4所示。
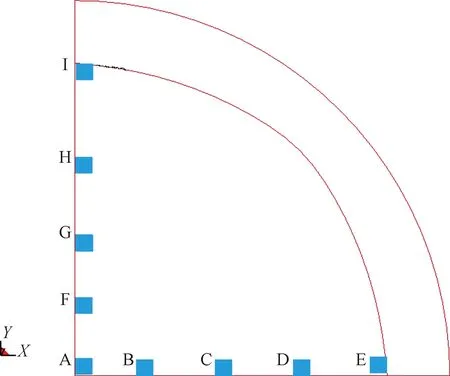
图3 封闭端超压数据采集点Fig.3 Overpressure data acquisition point at closed-end
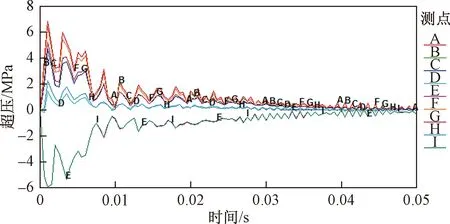
图4 封闭端壁面测点超压时程曲线Fig.4 Overpressure time curve of closed-end wall
从图3中可知,测点A、B、C、D、F、G、H变化趋势一致,另外,测点E和测点I超压变化趋势基本一致。封闭巷道整体的超压峰值整体变化为先增大后急剧降低,经壁面反射后,再次达到峰值,反复之后,趋于常压。由于爆炸冲击波并非以稳定的方式传播,而是在传播过程中不断变化,在不同方向上对巷道的损伤破坏会有所差别。从封闭端测点最大超压峰值来看,测点A最大,其次是测点B、E、C,最后为测点D,其中测点A最大值为6.92 MPa,测点E超压峰值为5.98 MPa,由于测点E在两壁面的交界处导致超压峰值变大。分析表明,在巷道壁面边缘位置和中心位置超压测值较大,其壁面损伤相对更为严重。
由此可知,由于巷道壁面的相互约束,封闭端超压变化变得更加复杂。测定均在爆炸区域,由于测点A在爆源位置附近,瓦斯爆炸具有瞬时性,测点A瞬间达到峰值,随着爆炸能量的衰减,整体超压测点值均呈现非线性衰减,最终趋于稳定值。瓦斯爆炸时,其他测点距离爆源位置较远,超压测点先后到达峰值,由于受到了瓦斯爆炸冲击波的连续干扰,冲击波在封闭端反复地反射和叠加,呈现出参差不齐的形状。
2.1.2 轴向壁面测点超压分析
巷道轴向数据采集点如图5所示,巷道轴向方向每隔2 m选取一个数据测点,J、K、L、M共4个测点。
从图6中可知,瓦斯爆炸后,冲击波在巷道轴向壁面也会出现反射和叠加,导致整体超压峰值上下振荡波动。J、K测点呈现衰减趋势,L、M超压测点先增加随后衰减趋势。这是由于瓦斯爆炸瞬间未达到空气区,导致超压峰值波动。最后,瓦斯爆炸超压趋于稳定。
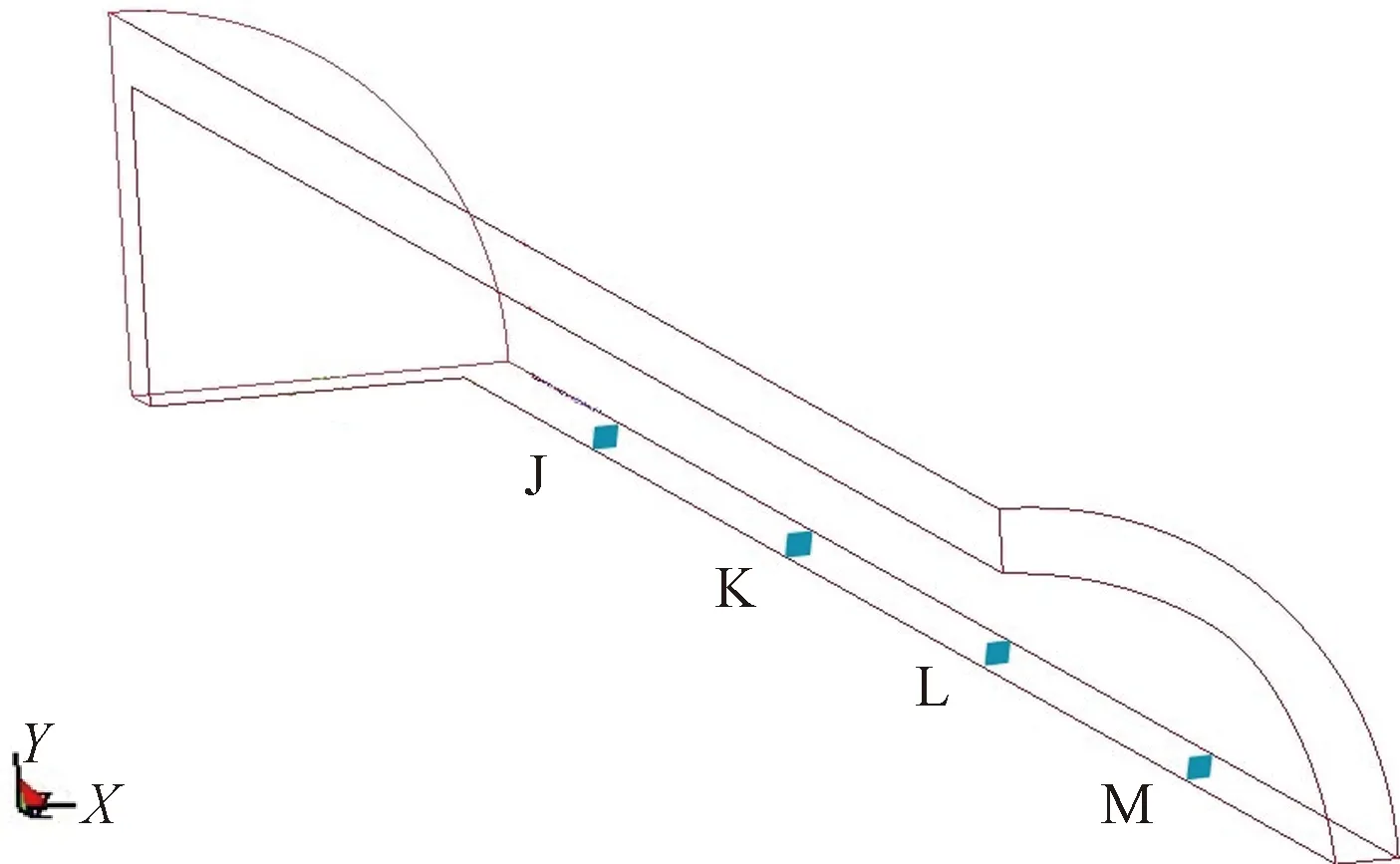
图5 轴向数据采集点Fig.5 Axial data acquisition point
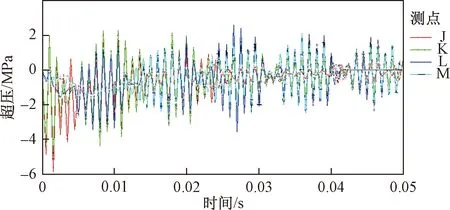
图6 轴向壁面超压变化曲线Fig.6 Axial wall overpressure curve
由此可知,在瓦斯爆炸后,冲击波向四周传播,在受到轴向壁面的限制下,冲击波会沿内壁传播,轴向超压呈现振荡起伏趋势。但随着瓦斯爆炸能量较少,爆炸超压整体衰减并趋于稳定。测点L最大峰值达到5.9 MPa,测点K峰值达到5.0 MPa,但都大于测点L、M,这是由于测点L、M位于空气区,瓦斯爆炸冲击波未直接达到空气巷道壁面,测点同时也受巷道壁面限制,超压测点出现上下波动。随后超压整体呈现衰减趋势。
2.2 壁面云图分析
2.2.1 封闭端云图分析
图7所示为在不同时刻下封闭端壁面超压变化云图,可知瓦斯爆炸后在封闭端压力较大位置为中间位置和边缘位置。超压区域呈现环状并向四周递减。随后超压区域不断扩展布满整个封闭端断面,在封闭端由于受到壁面限制,超压反射叠加达到峰值为6.12 MPa,同时壁面中间位置超压为3.95 MPa。然后,由于封闭端减负压的作用,封闭端壁面会再次受到二次冲击,对壁面造成更进一步的损伤破坏。
在封闭端云图中,可以看出封闭端应力随时间变化趋势,在瓦斯爆炸后,爆炸较大应力首次出现在封闭端中心区域,封闭端周围自由度受到限制。拱形区域应力不明显,说明其所受应力最小。随着反应的进行,封闭端壁面所受应力逐渐积累,使其遭受损伤破坏。

图7 封闭端壁面超压变化云图Fig.7 Closed-end wall overpressure change nephogram
2.2.2 轴向壁面云图分析
图8所示为巷道轴向壁面超压变化云图,从图中可知,瓦斯爆炸后,冲击波载荷首先加载到巷道内壁面上,超压作用促使壁面结构产生应力,并逐渐向外壁传递,随着爆炸反应的进行,能量逐渐衰减。在轴向上,瓦斯爆炸后冲击波沿轴向向开口方向传播,冲击波首先加载在瓦斯区壁面结构并逐渐向空气区壁面加载。瓦斯区壁面受到的载荷最大,随后向空气区壁面扩散。
轴向壁面应力云图呈现环状分布,沿巷道轴向方向扩散。其应力加载不是均匀扩散,其壁面的应力变化随着时间的增大而增大,在边缘区域逐渐发展到壁面中间区域。随后轴向壁面出现了环状应力变化,其爆炸载荷不断向壁面加载,不过应力不断变小,在部分区域应力集中,这些区域往往是巷道壁面最先出现损伤破坏的区域。
2.2.3 壁面破坏特征分析
在瓦斯爆炸后,冲击波最先冲击封闭端面,使其遭受损伤破坏,并且壁面中间位置损伤最严重,说明瓦斯爆炸后,巷道壁面结构在爆炸载荷作用下,随着反应的进行壁面区域破坏损伤沿壁面结构轴向扩散。冲击波传到壁面结构后,首先压缩波从内表面向外表面传播,之后压缩波从外表面拉伸形成拉伸波,沿巷道壁面结构向外扩展。
壁面损伤破坏主要是爆炸冲击波的动力破坏和爆轰气体准静态破坏的综合破坏结果。爆炸瞬间冲击波的动态应力促使壁面产生环形压缩应力,随着爆炸冲击波能量衰减,一部分能量通过对流、热交换损失,一部分转化为应力波,壁面结构在应力波的叠加作用下再次受到拉伸破坏,应力波加载再次加剧,造成更加严重破坏。冲击波能量减少,而应力持续加载在壁面结构,压力集中对壁面结构施加静态破坏,最后超过其承受能力,导致巷道失稳破坏。

图8 轴向壁面超压变化云图Fig.8 Axial wall change nephogram
3 结论
通过利用ANSYS/LS-DYNA动力学软件对巷道中瓦斯爆炸破坏过程的数值模拟,形象地反映出爆炸过程中超压及云图变化过程,由此得出以下结论:
(1)在巷道壁面边缘位置和中心位置超压测值较大,其壁面损伤相对更为严重。因此应该避免大物体堆放及加强其相应位置防护。
(2)瓦斯爆炸后,冲击波在巷道轴向壁面也会出现反射和叠加,导致整体超压峰值上下振荡波动。
(3)瓦斯爆炸后冲击波向开口方向传播,瓦斯区壁面受到的载荷最大,并逐渐向空气区加载扩散。
(4) 随着爆炸冲击波能量衰减,而应力持续加载在壁面结构,压力集中对壁面结构施加静态破坏,最后超过其承受能力,导致巷道失稳破坏。
