基于改进遗传算法的车间调度原型系统
2020-04-24车志忠张富强惠记庄
郭 岳, 朱 斌, 车志忠, 戴 博, 张富强, 惠记庄
(长安大学公路养护装备国家工程实验室,西安 710064)
当前,制造业进入以智能制造为代表的工业4.0时代,随着用户对于产品制造要求不断提升,以制造执行系统(manufacturing execution system,MES)为核心的先进制造技术已成为研究的热点[1]。车间调度作为MES系统中的关键业务,也是提高制造业生产效率的关键因素[2]。车间调度问题(job-shop scheduling problem,JSP)和柔性车间调度问题(flexible job-shop scheduling problem,FJSP)都是经典离散组合优化问题[3],数学上属于NP难题[4]。
中外学者采用不同的求解算法对车间调度问题进行了深入研究,其中遗传算法作为一种鲁棒性强、通用性好的智能优化算法,在车间调度问题中得到了广泛应用[5]。但传统遗传算法存在全局搜索能力和局部搜索能力较差,并容易早熟收敛等问题。对于遗传算法的改进已经有众多的研究成果。Gao等[6]针对柔性车间调度问题提出一种经典的混合遗传算法。陆曈曈等[7]针对柔性车间调度问题提出一种改进元胞遗传算法。石小秋等[8]为解决车间调度问题,提出了一种自适应变级遗传杂草算法,分析了求解参数对算法性能的影响。王秋芬等[9]基于集合论数学模型,研究了两层编码在解决车间调度问题的应用。Wang等[10]针对逆向作业车间调度问题,提出了一种基于十进制机制的分组编码方案,该方案可以同时优化过程和参数。何斌等[11]针对车间调度问题,提出通过动态改变交叉与变异概率提高算法的寻优能力。赵诗奎等[12-13]为提高遗传算法求解车间调度问题初始种群的质量,提出了启发式方法与基于短用时和设备均衡策略的机器链优化方法。宋存利[14]提出了改进贪婪遗传算法,采用了正序解码和逆序解码加再调度并用的解码策略。
这些研究主要集中在种群初始化、遗传操作、解码、以及其他算法融合等方面。可以看出,目前在构造遗传算法初始种群方面方法过于复杂,没有解决初始种群大小难以确定(一般通过经验或测试)、初始解稳定性差、初始化种群多样性难以保证[12-13]和不利于遗传操作过程的问题,且整个算法在实际车间调度系统实现上还存在一定的困难。为此在遗传算法求解车间调度问题的基础上引入幻方变换编码机制,产生自适应问题规模的初始种群,直接对幻方变换产生的互换编码种群进行遗传操作,简化了遗传操作的复杂度;针对车间调度问题和柔性车间调度问题进行综合考虑,不再将JSP问题当作FJSP问题处理,充分分析了两者差异,并融入到遗传算法中;最后在此基础上对这两类问题和上期工序遗留问题进行了原型系统开发,并对改进遗传算法的有效性进行了验证。
1 车间调度问题描述
车间调度问题作为一类特殊的排序问题,其目的是在给定的机器资源约束下,在不破坏事务技术顺序的前提下,完成多个事务的合理资源分配[15]。其数学上可以描述为n项事务在m种资源下按照给定约束有序进行,其数学模型如下:
(1)机器资源集M={me1,me2,…,mem},mej表示第j种资源,j=1,2,…,m。
(2)事务集J={jo1,jo2,…,jon},joi表示第i个事务,i=1,2,…,n。
(3)事务顺序集JM={jm1,jm2,…,jmn},jmi={jmi1,jmi2,…,jmil}表示事务i的技术顺序。
(4)可选机器集OPM={jmi1,jmi2,…,jmil},jmil={jmil1,jmil2,…,jmils}表示事务的技术步l可以选择的机器资源。
(5)机器处理事务时间矩阵T,til∈T,表示第i个事务在机器l上的加工时间。
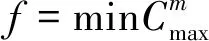
2 改进遗传算法
基于以上数学模型,改进遗传算法流程如图1所示,根据求解问题类型的不同,JSP问题采用单层编码,FJSP问题采用多层编码,并利用幻方变换法初始化种群,进行遗传操作,直到达到最大遗传代数,再将最优染色体按求解问题类型和解码规则生成调度方案。
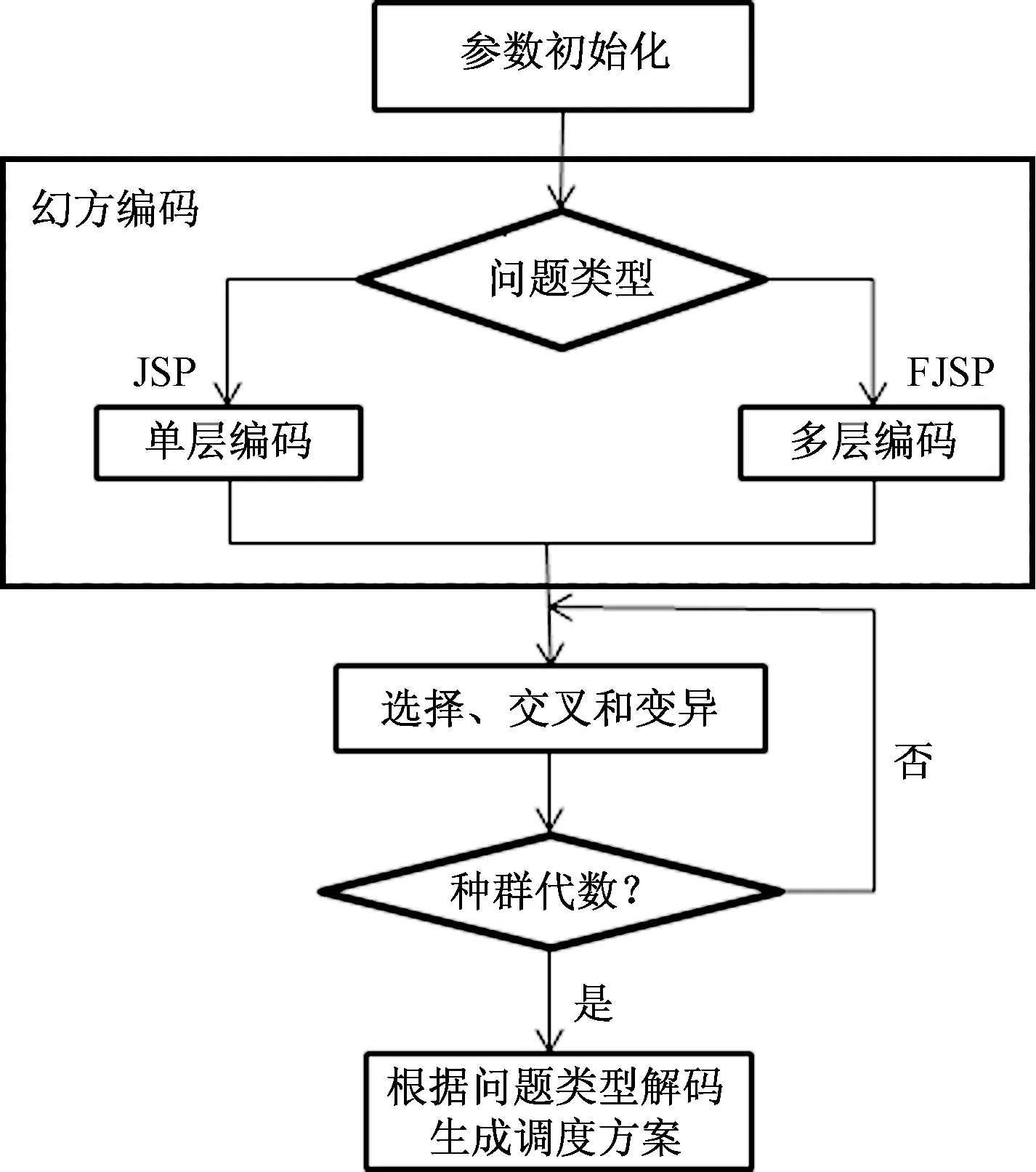
图1 改进遗传算法流程Fig.1 Flow chart of improved genetic algorithm
2.1 初始化种群
为了保证遗传算法种群的多样性,同时提高初始解的质量,目前车间调度问题多采用互换编码、随机编码、NEH启发式编码[16]和量子比特编码[17]等,这些编码方式都存在遗传操作过程过于复杂的问题,为此,提出基于规则的幻方变换互换编码。互换编码主要用于解决一维排序问题,如旅行商问题,车间调度问题可以看成是带约束的多旅行商问题(multiple traveling salesman problem, MTSP)[18],即多个工件在机器上的流转,只是需要添加技术约束条件(工件在机器上的加工次序)。车间调度问题编码可以看成一维旅行商问题,即对所有工件工序进行互换编码,并对互换编码进行切片以产生满足车间调度问题的工序编码。对于JSP问题工件工序和加工机器是一一对应的。采用基于工序的单层编码就足以解决;而对于FJSP问题,则需要根据工序可选机器集生成机器码层,然而机器码层可以看作工序编码层的子层,只要跟随工序码层做相同的遗传操作,就能求解FJSP问题,因此下文只对单层编码过程进行介绍。
2.1.1 互换编码与工序编码的关系
设一条染色体X={x1,x2,…,xJn},x为1~Jn的整数随机排列,对其进行切片映射即可产生工序编码的染色体X′={x′1,x′2,…,x′Jn},其中x′k=i(1≤i≤n,1≤k≤Jn),若x′k为染色体X′中x′1到x′k的第j个i,则x′k表示工件i的第j道工序。图2所示为4个工件,各工件工序数为3、3、4、2的互换编码到工序编码的切片映射生成过程。至此问题转化为基于工序的互换编码问题。下面开始构造互换编码。
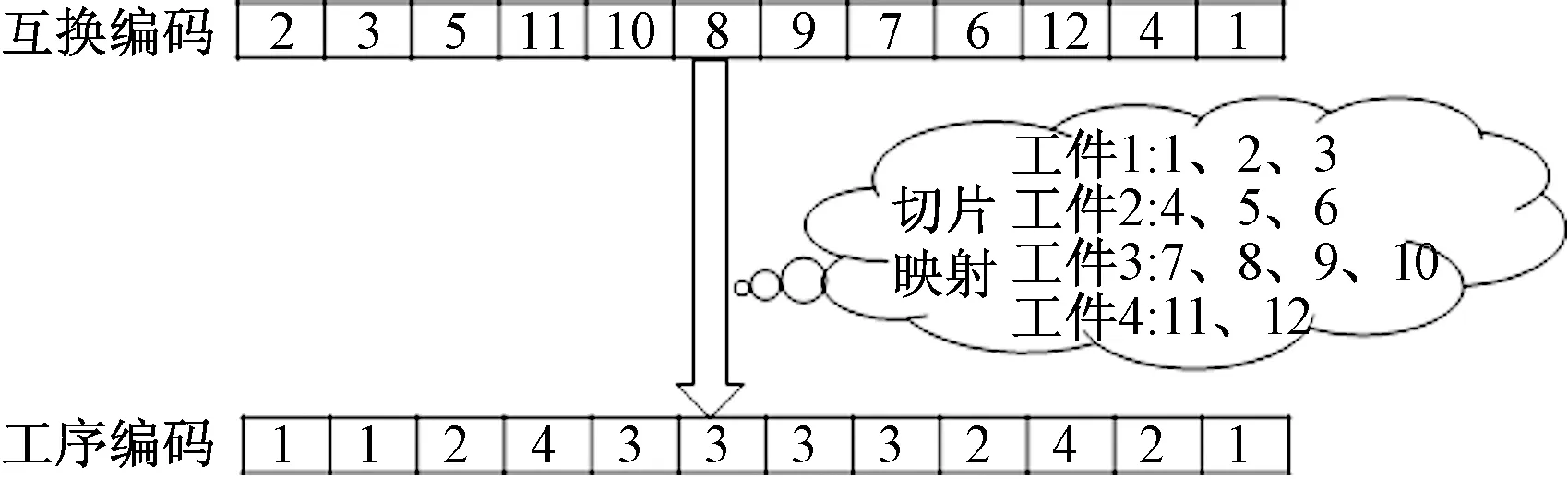
图2 互换编码与工序编码映射关系Fig.2 Interchange coding and process coding mapping
2.1.2 幻方种群构造方法
幻方是起源于我国的神秘的数学问题,其在人工智能、对策论、实验设计、工艺美术、电子回路原理、位置解析学等方面有着广泛的应用,并逐步成为组合数学研究的重要课题[19]。
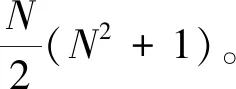
下面结合幻方矩阵构造工件工序总数为12的初始种群,具体步骤如下:
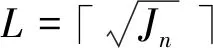
(2)幻方变换,对幻方矩阵依次逆时针旋转c×90°<360°,其中c=1、2、4,c为初始种群规模因子,控制种群大小。图3所示为4阶幻方旋转变换过程。
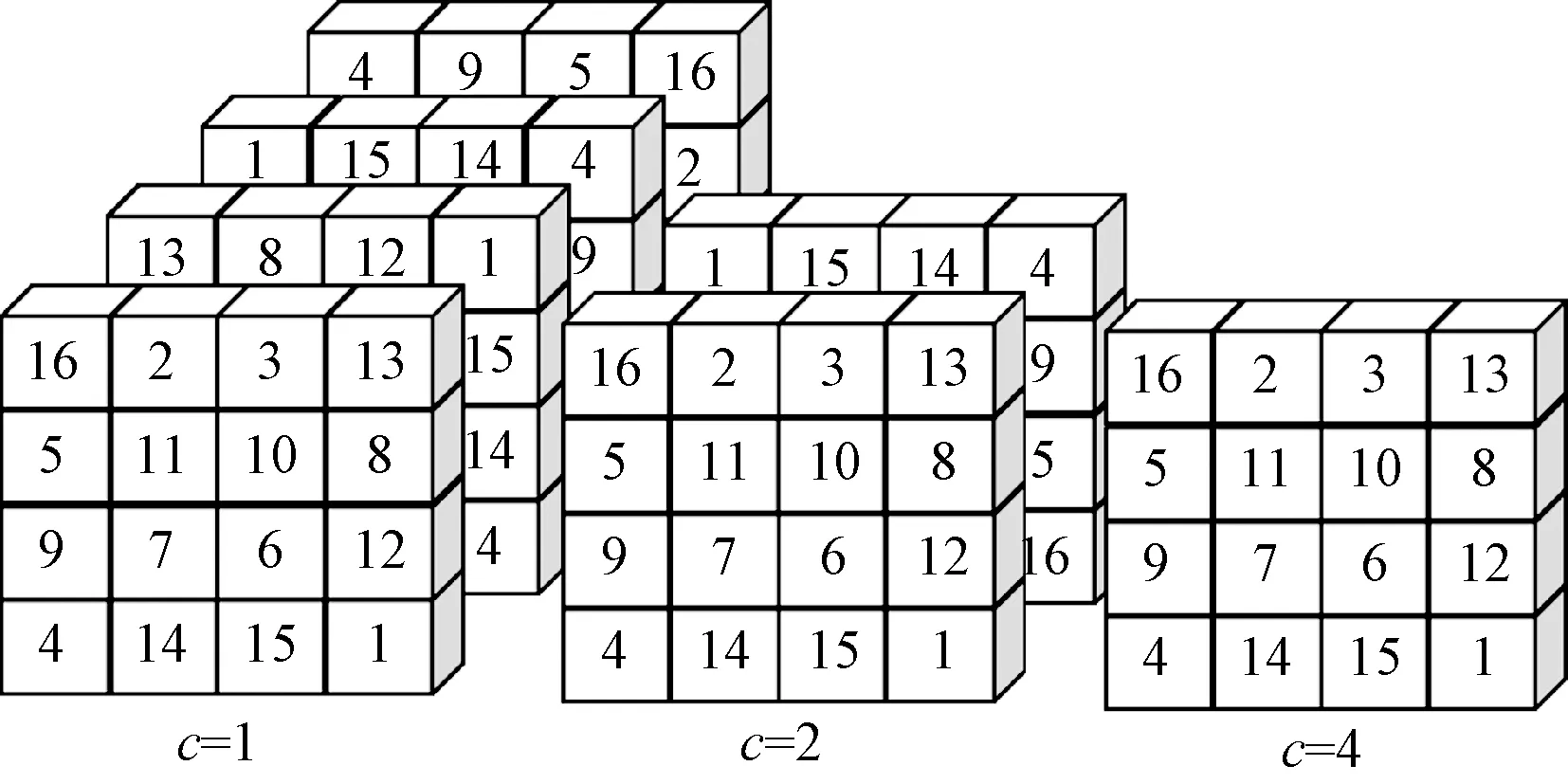
图3 4阶幻方旋转变换Fig.3 4th-order magic square rotation transformation
(3)取步骤(2)中幻方矩阵记为A,对A矩阵作初等行变换E(i,j)A,其中i,j∈[i,L],且i≠j,E(i,j)为初等矩阵。图4所示为步骤(2)旋转变换后的幻方进行行变换过程,每一个4阶幻方被变换为一个数据立方体。
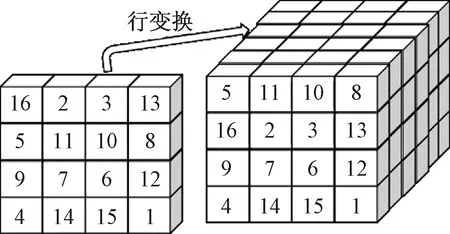
图4 4阶幻方行变换Fig.4 4th magic square row transformation
(4)对幻方变换数据立方体进行拉直,去除大于Jn的数据,产生初始种群。图5所示为4阶幻方变换数据立方体经过拉直调整生成初始种群的过程。
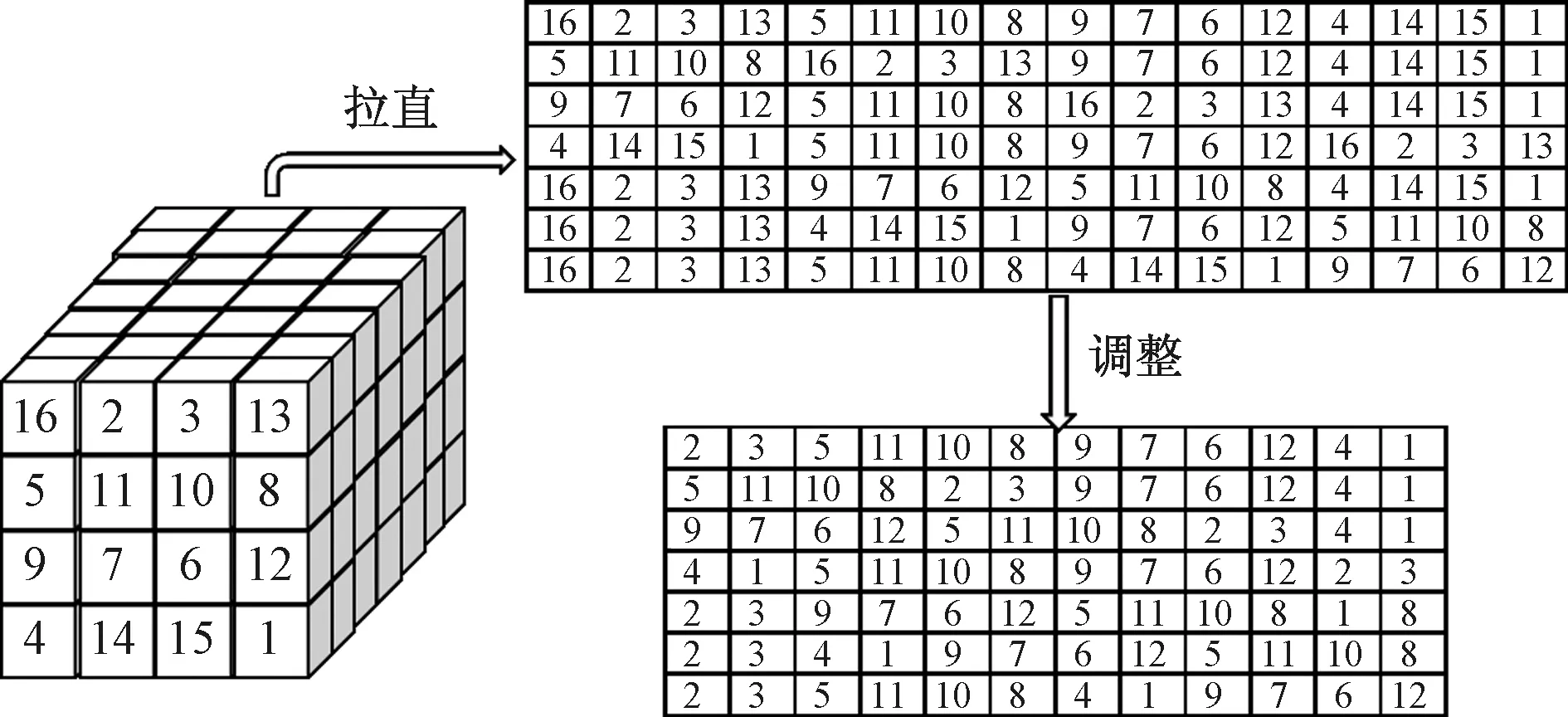
图5 4阶幻方种群生成过程Fig.5 4th-order magic square population generation process
2.1.3 种群规模
在遗传算法初始化时,种群规模设置过大会导致算法计算量增加、效率降低。经验得知,种群规模通常取[10,200],具体大小可根据染色体基因位数估算确定。现提出的构造初始种群机制,产生的种群个体为幻方阶数的函数,而幻方阶数又可以通过基因位数得到,所以可近似认为种群数与基因位数存在某种模糊关系,式(1)为其种群规模与幻方阶数L的关系。
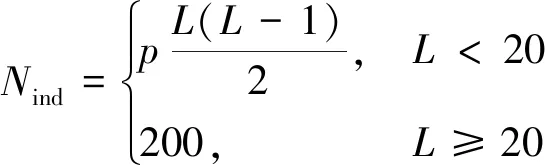
(1)
式(1)中:Nind为种群中个体数量;参数p与种群规模因子c有关,满足表1的关系。

表1 参数p与因子c的关系
可以验证在工件总工序数Jn与L2相差不大时,所产生初始种群的个体具有多样性。
2.2 选择操作
对于车间调度问题常采用所有机器中最大加工时间作为适应度函数。那么适应度为

(2)
式(2)中:Eval为种群中适应度值;m为机器数。
陶俊波等[20]提出通过个体好坏的排序(并非原始适应值)确定个体选择概率,可以防止优秀个体过度繁殖,进而避免算法过早收敛。基于排序的适应度分配选择步骤如下:
(1)由于种群中个体适应度越小,调度方案越优,所以对种群中个体按照适应度大小进行从小到大线性排序。
(2)种群中排序为i的个体分配适应度为
(3)
式(3)中:sp为选择压差,决定偏移和选择强度。
(3)按照种群中个体分配适应度值进行“比例选择”,即所谓的“轮盘赌”。
2.3 交叉操作
种群通过交叉操作可继承父代的优秀基因片段,从而推动整个群体的进化历程。对于车间调度问题,为了尽可能多的继承父代优秀基因片段,这里采用单点交叉,即交换父代两个染色体中交叉点之后(或之前)的基因片段,产生子代个体,具体操作步骤如下:
(1)根据交叉概率选择两条交叉染色体,并随机产生交叉位置Pos。
(2)将父代个体交叉点之后的基因片段进行交换,并找出在非交叉位置的不合法基因位。
(3)依次交换不合法基因位产生子代个体。
图6所示为种群中随机选择的两条染色体进行单点交叉操作过程,图6(a)随机生成交叉位置Pos,图6(b)交换Pos位置之后的基因片段,并且标记交叉点之前重复基因位,图6(c)交换交叉点之前基因位所产生的两条子代染色体。
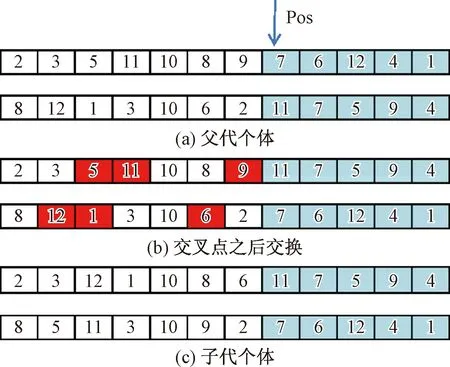
图6 单点交叉操作过程Fig.6 Single point cross operation process
2.4 变异操作
变异算子采用的是两点换位法,首先根据变异率选取染色体X={x1,x2,…,xJn},在染色体X上随机选取两点i、j,将这两个点上的基因位进行互换,生成新的子代染色体X*={x1,…,xj,…,xi,…,xJn}。
2.5 解码
由于JSP问题和FJSP问题编码方式的不同,编码位含义不同,那么解码也就存在一定的差异。虽然两种问题解码具体过程存在差异,但解码的过程可以统一,即实现染色体到加工描述矩阵的映射。
为描述某一工件某道工序的加工过程,需要4个参数,分别为工件号、工序号、机器号和加工时间,这一事件记作D=(X,XP,XM,XT),其中D为加工描述矩阵,D中各元素分别表示工件编码序列、以工件编码序列所对应工序序列、机器序列和加工时间序列。
对于染色体X={x1,x2,…,xJn},解码步骤如下:
(1)染色体切片,将互换编码通过切片转化为工序编码的染色体X′={x′1,x′2,…,x′Jn},其中x′k=i(1≤i≤n,1≤k≤Jn)。
(2)按照染色体X′工件加工顺序,对照工件工序集产生染色体X′的对应加工工序序列集XP、加工机器序列集XM和对照XP和XM产生染色体X′对应的加工机器时间序列集XT。
(3)定义机器上工件开始加工时间矩阵、机器当前时间数组和机器上工件结束加工时间矩阵,判断问题类型有无上期遗留未加工工序,如果存在工序遗留,那么机器当前时间数组应该为上期未加工工序各机器遗留时间。
(4)解码过程需做如下逻辑判断,如果某工件首次加工或待加工工件机器当前时间大于该工件上道工序加工完成机器时间则直接开始当前工件加工,否则机器等待工件上道工序加工完成,才能进行当前工序加工。
3 调度原型系统
作业车间调度作为MES生产计划的一个主要功能模块,其需要提供MES生产计划数据接口,完成对车间作业计划工艺和设备等信息的采集和处理,通过自身的排程功能,生成资源分配计划,传回MES系统,以便进行后续的动态调整和生产执行。
3.1 原型系统设计
作业车间调度系统(图7)中包含对工件、机器、工艺和排程的管理。工件管理完成调度工件的添加和移除;机器管理包括对机器号和机器状态的设定;工艺管理包括加工状态修改;排程管理包括问题类型、排程参数的确认、求解参数设定、查看求解过程和排程结果展示。
3.2 排程展示和功能验证
采用文献[21]提供的某钢桥算例来展示排程管理结果,实验数据如图8所示,程序为面向对象的、运行于.NET Framework和.NET Core之上的高级程序设计语言C#开发,参数设置如下:迭代次数为50,交叉概率为0.8,变异概率为0.1,种群规模c取1,对应的种群大小为88,上期各机器遗留任务所需时间均为10。图8和图9所示为其排程参数设置和排程结果,图10所示为每代求解结果和平均求解结果的变化情况。
为了验证本文提出的改进遗传算法的有效性,采用文献[9,11,21]中相同数据集进行测试。算例1为Ft06基准算例,算例2为8×6算例,算例3为工程测试案例。文献[9]采用两层编码并对适应度度量和遗传算子进行优化的改进遗传算法;文献[11]采用动态交叉和变异算子的改进遗传算法;文献[21]采用标准遗传算法进行求解。为了对本文提出的种群初始化方法的有效性进行验证,可对测试算例的10次实验结果的第一代最优值及第一代所有个体适应度平均值进行对比[12-13]。表2列出了3个算例的第一代求解结果和最终求解结果,将求解结果与相关文献求解结果进行比较可以看出,提出的种群构造方法在第一代就能得到相对优秀的个体,优于其他文献中的初始种群构造方法,采用自适应种群为工程测试案例大小,当种群规模较小时,仍然能够得到较优的结果,表明该算法构造种群具有良好的多样性。算法最终求解结果等于或优于文献结果,验证了该求解算法的有效性。

图7 车间调度系统组成Fig.7 Composition of the shop scheduling system
图8 排程参数设置界面Fig.8 Scheduling parameter setting interface

图9 排程结果展示界面Fig.9 Scheduling results display interface
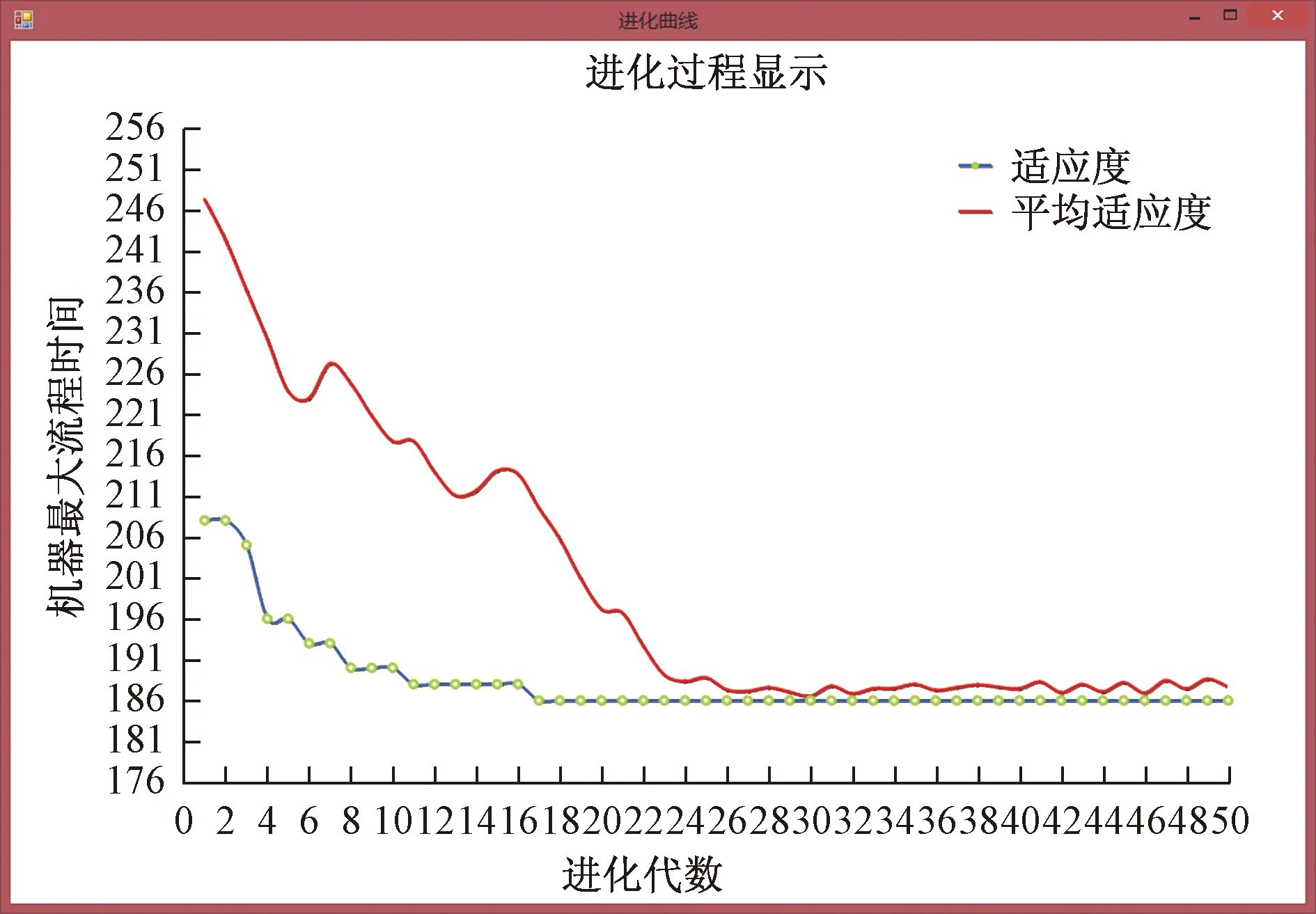
图10 改进遗传算法求解过程Fig.10 Improved genetic algorithm solution process

表2 改进遗传算法求解结果对比
4 结论
对车间调度问题的研究得到以下结论:
(1)遗传算法进行基于幻方变换的互换编码和基于规则的解码设计,减小了种群染色体的空间复杂度,简化了遗传算法求解车间调度问题的编码过程,提高了遗传算法的求解能力。
(2)采用互换编码进行遗传操作有效简化了交叉和变异过程,为实际调度问题的解决提供理论支持。
(3)在微软.NET平台采用C#语言构建了用于同时求解JSP、FJSP和上期工序遗留问题的调度原型系统,为搭建更加符合生产实际的车间调度系统提供了参考。
