Three dimensional nonlinear shock waves in inhomogeneous plasmas with different size dust grains and external magnetized field

Liping ZHANG (张丽萍),Jun FU (付君) and Junyan SU (苏俊燕)

School of Sciences,Lanzhou University of Technology,Lanzhou 730050,People’s Republic of China

Abstract

Keywords:shock structures,inhomogeneity,nonadiabatic dust charge fluctuation,dust size distribution

1.Introduction

Dust plasma exists widely in laboratory,space and other environments.The appearance of negatively charged dust particles will greatly change the collective behavior of plasmas and introduce new nonlinear structures [1–5].The solitary waves and shock waves are the most common nonlinear structures.In dusty plasmas,the steepening of nonlinear waves can be balanced by the dissipation induced by dust charge fluctuation,which excites stationary shock waves.During the past decade,the investigation of nonlinear shock structures in dusty plasmas has attracted extensive attention[6–8].In a uniform double dusty plasma device without magnetized field,the formation of the shock waves had been experimentally found and experimental results had shown that the oscillation at the leading part of shock waves had disappeared and a monotonic shock structures had been found when the dust density was larger than the critical value [9].The evolution of shock structures was experimentally investigated in a single layer Tangchuan hexagonal lattice composed of monodisperse plastic microspheres and it has been found that there were phase transitions due to the existence of shock waves [10].Sahu et al [11]have investigated the nonlinear evolution of arbitrary and small amplitude shock waves in a dusty plasma with external magnetized field but without dust charge fluctuations,and found that when the dissipation effect caused by the viscosity was dominant,the oscillatory feature of shock structures disappeared,i.e.the monotonic shock waves appeared.The shock structures in four component plasmas comprising of two temperature superthermal ions with kappa-distribution,dust fluid and Maxwellian electron have been reported by Ghai and Saini[12].They reported that the amplitude of positive shock waves governing by Burgers equation decreases but the amplitude of modified shock waves with higher order nonlinearity increases with superthermality of cold ions.

In reality,the dust particles have different sizes either in space plasmas or the laboratory plasmas.Generally,the size distribution of dust gains can be governed by a Gaussian distribution in laboratory plasmas,however,the size distribution of dust gains is described using power law distribution in space plasmas.The effects of particles size distributions on polymethyl methacrylate dust flame propagation behaviors have been experimentally investigated in polymethyl methacrylate dust clouds with same Sauter diameters[13].Duan et al investigated the evolution of damping solitary waves with different size particles and research results manifested that the solitary wave damping rate in a dusty plasma with different particle sizes is higher than that of ordinary particles [14].The influence of different size dust grains on the propagation characteristics of dust acoustic waves in dusty plasmas was studied and research results revealed that the rarefactive waves can primarily exist in plasma model while compressive waves can exist in the case of a small range of plasma distribution parameters,and the dust acoustic waves have a faster propagation speed and a wider propagation range for smaller size dust particles [15].Furthermore,the inhomogeneity and the dust charge fluctuation exist widely either in the laboratory or space plasmas.It is necessary to study the effect of the dust charge fluctuation,dust size distribution and the inhomogeneity on the evolution of shock waves in dusty plasmas.

In this work,we investigate the characteristics of three dimensional nonlinear shock waves in an inhomogeneous magnetized dusty plasma consisting of negatively charged dust particles with variational charges and different size,Boltzmann distributed electrons and nonthermal ions.The dynamical equations are presented for the evolution of shock structures by employing the derivation of modified nonlinear Korteweg-de Vries (MKdV) Burgers equation with variable coefficients.The influence of dust charge variation,magnetized field,dust size distribution,inhomogeneity and evolution angle on the propagation of shock waves is investigated.

2.Governing equations

Suppose the particles in the plasmas are in a thermal equilibrium state,the electrons obey the Boltzmann distribution.So,let us consider a magnetized dusty plasma composed of dust grains whose size is different and charge varies,nonthermal ions and Boltzmann distributed electrons.In a external magnetic field (B=Bx0) with fixed intensity,the number density of this system has a gradient along the x direction.At equilibrium,the quasi neutrality condition can be given as,whereZdj0(x)is the charge number on the jth dust particles,ndj0(x),ne0(x)andni0(x)are jth dust grain,the unperturbed electron,and ion densities,respectively.The basic equations describing the mechanics of this system can be written as

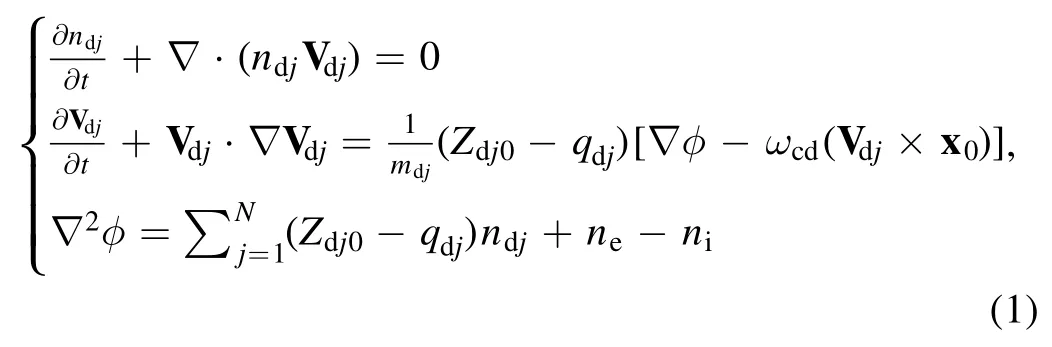
where the jth dust grains’ velocity Vdj=(udj,vdj,wdj)is normalized by the dust acoustic speedCd=(Tiis the ion-temperature),is the average dust grains’mass,andis the average dust charged number;n jdandniare the number densities of dust grain and ions normalized by Ntotandni0,respectively.φ is the dimensionless electrostatic wave potential.The space variable x and time variable t are normalized byandrespectively.wcdis

The distribution function of nonthermal ions is [16]:whereαis the parameter determining number of nonthermal ions.The number density of electrons with Boltzmann distribution is:where

Qdj=is the jth dust particle’s charge,whereq jdrepresents the normalized charge fluctuation of the jth dust particle.In order to obtain the normalized variableq jdof dust charge,the normalized balance equation of orbital motion-limited [17]charge current is

where Iiand Ieare the ion and electron current,respectively.It is supposed that the electron gyroradius (ρe) is much larger than the dust grain radius (a),which means that the effect of curvature on the trajectories of ions (electrons) traveling into dust particles with radius a is negligible [18,19].Thus,considering spherical dust particles with radius a,the dimensionless expressions of electron currents obeying Boltzmann distribution and that of ions obeying nonthermal distribution are [20]

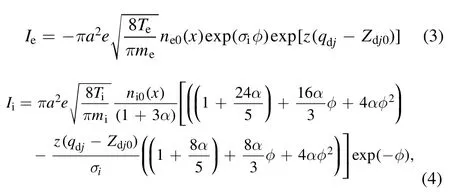
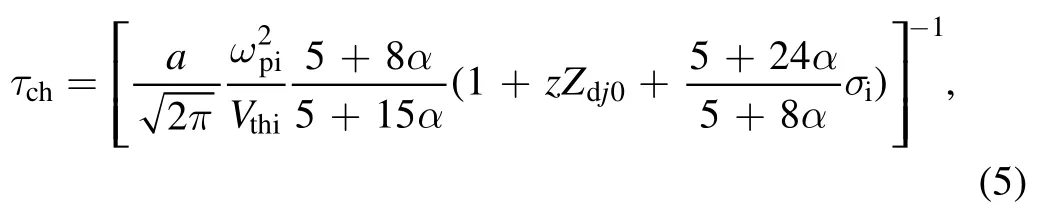
3.Nonlinear wave propagation equation

In order to obtain MKdV Burgers equation describing shock structures,we use the standard reductive perturbation technique [21].According to this technique,the stretched coordinates are:

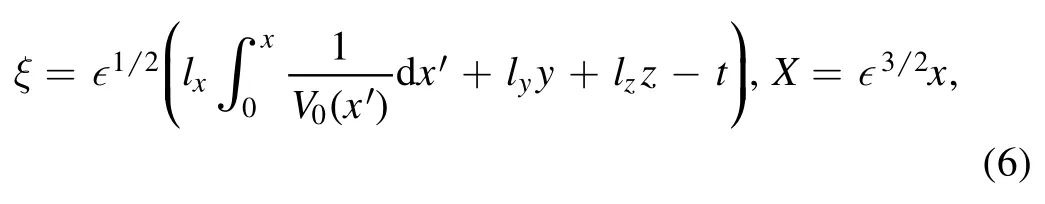
where є measures the weakness of nonlinearity,V0(x) is the velocity of the moving frame to be determined later.Substitutingndj=ndj0(X)+єndj1+є2ndj2+...,[22]into equations (1) and (2) and gathering the same power of є,we get:whereandβ1=

We obtain a set of equations at the second order of є:

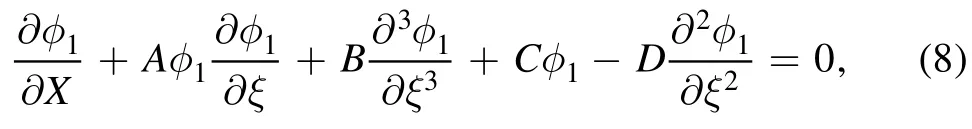
Equation(8)is the MKdV Burgers equation with variable coefficients describing the characteristics of nonlinear shock waves in a nonuniform magnetize dusty plasma by considering power law dust size distribution and the nonadiabatic variation of dust charge.For inhomogeneous dusty plasma without dust size distribution,the coefficients of A,B,C and D reduce towhich is the same as the result in our earlier work [23].

4.Approximate analytical solutions for the MKdV Burgers equation

Now we seek the analytic solution of MKdV Burgers equation (equation (8)).We set φ1towhereSubstituting it into equation (8),then the standard KdV Burgers equation with variable coefficients for φ can be obtained,

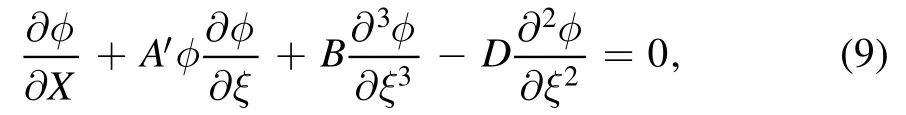
whereA＇=Aφ10.As is known to all,the profile of weak shock waves can be described by the KdV Burgers equation and there is the condition that the shock waves exist,that is,D＞0.No considering the nonadiabatic fluctuation of dust charge,the coefficient D is equal to zero.Then,the KdV Burgers equation,equation (9) turns into standard KdV equation governing the nonlinear evolution of solitary waves.

It is obvious that it is very difficult to obtain the explicit solutions of equation (9),we try hard to find an approximate solution.It is supposed that the variation of equilibrium quantities with X is slow,at one fixed position X0the variable coefficients ＇A B,,and D in equation(9)are evaluated.Then,we obtain a local stationary solution in a coordinate system moving with velocity U.Applying the transformation with a traveling variableη=UX-ξ,the KdV Burgers equation (9) is rewritten

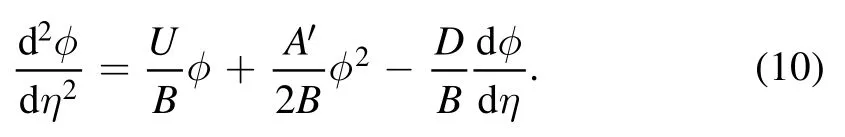
At the upstream regionη→∞,the integration constant has been set to zero according to the boundary conditions ofWe set φ=φcandat the downstream region(η→∞).So,the shock amplitude is

In order to investigate the downstream area’s asymptotic characteristics of equation (10),we take the following transformation [24]on the basis of nonlinear dynamics theory

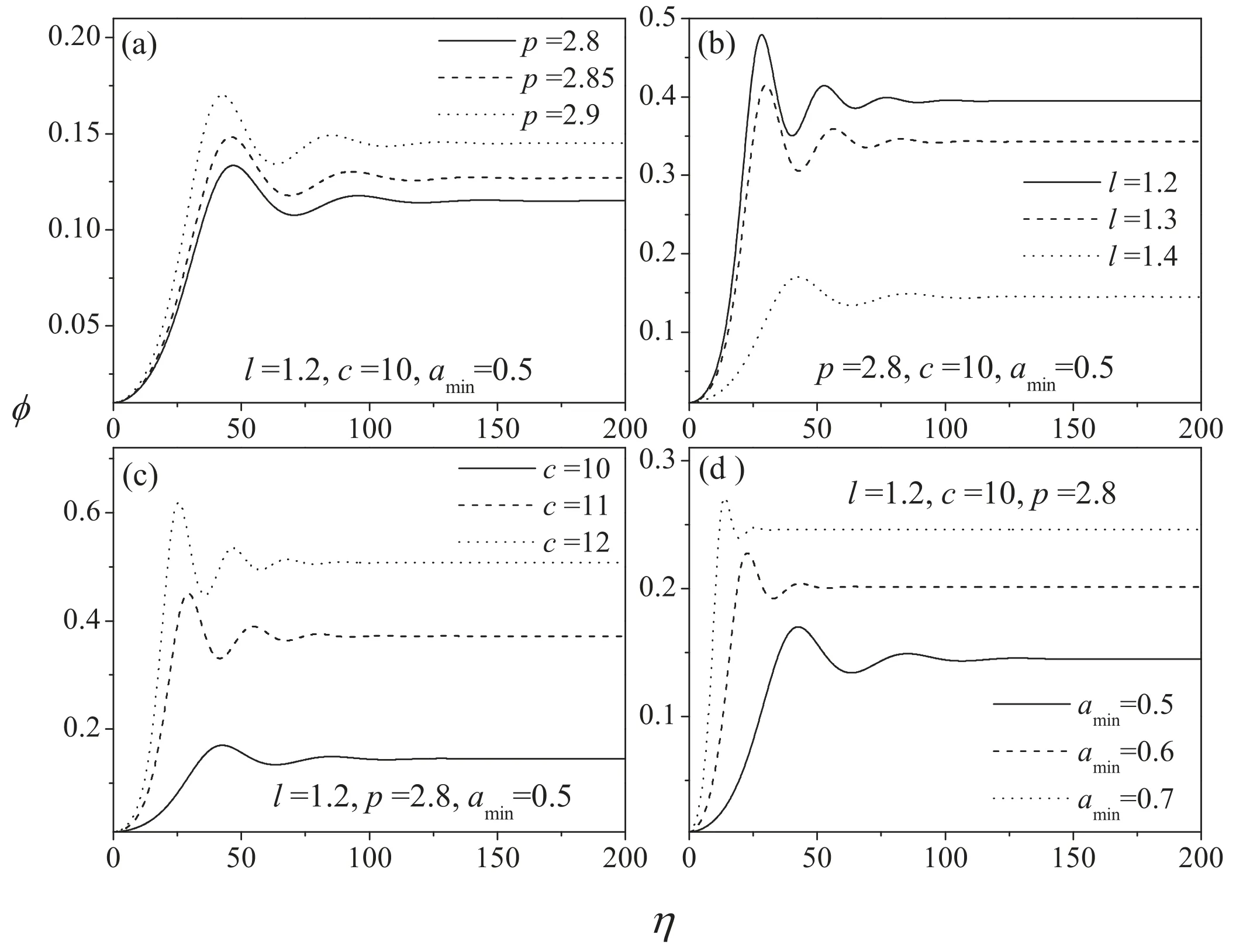
Figure 1.Profiles of shock waves for nd0=0.6,X L=0.8,α=0.2,σi=0.8,ν=1.2,lx=0.95,wcd=0.2.

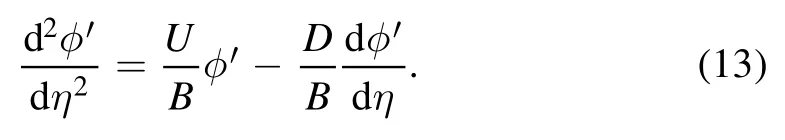
The solution of equation (10) is proportional to (λη) exp,where

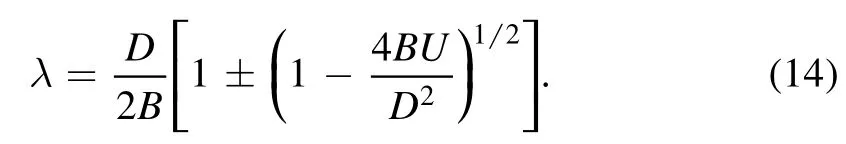
It is indicated from equation(14)that a monotonic property of the shock waves occurs whenhowever,an oscillatory property of the shock structures presents whenWhenthe asymptotic solution of equation (13) governing oscillatory property of the shock waves is

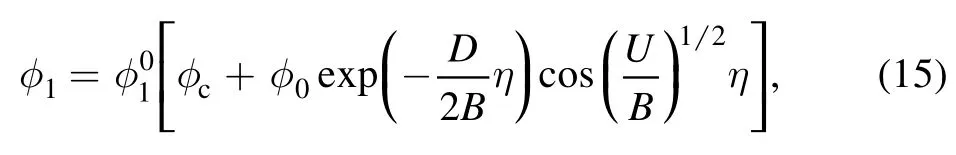
where φ0is a constant.From equation(15),the variation ofφ10in connection with inhomogeneity of dust density and dust charge causes changing of the shock amplitude.

5.Results and discussion

It is supposed that the radius of dust grains ajis much smaller than λDd,the charge and mass of dust particles arerepresents the mass density of the dust particles,Φ0represents the equilibrium electric surface potential,ε0represents the vacuum permittivity.

In space plasmas,the distribution of dust size obeys the power law distribution (n(a) da=Ka-pda).So the total number density is

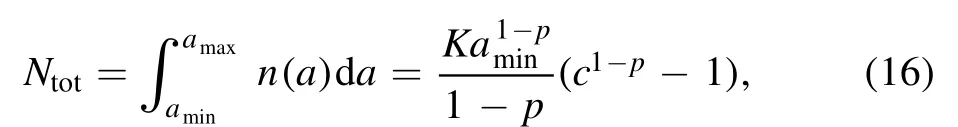
where p represents the power law index,=cThe dust particle radius is normalized according to the average dust particle radius

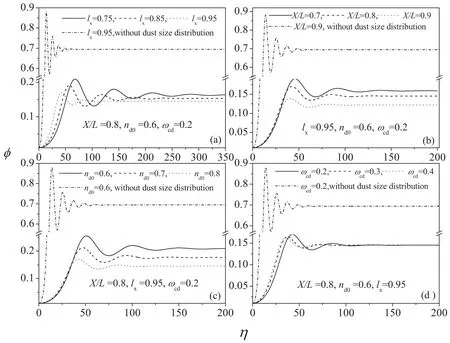
Figure 2.Profiles of shock waves for p=2.8,l=1.2,c=10,amin=0.5,α=0.2,σi=0.8,ν=1.2.

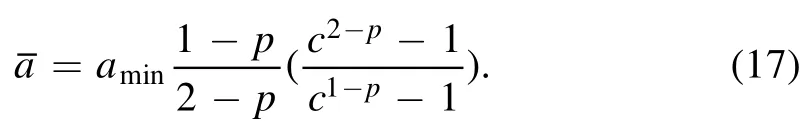
As a general rule,the number density of dust particles depends on both the inhomogeneity(X)and the distribution of dust size in plasmas.Considering that inhomogeneity and the distribution of dust size are independent of each other,the number density of dust particles about X and a is

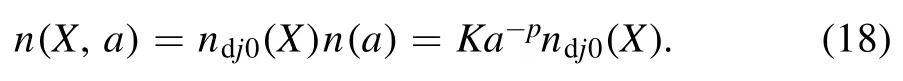
The charge on dust particles at equilibrium also depends on inhomogeneity X and dust size distribution.The charge on dust particles at equilibrium is

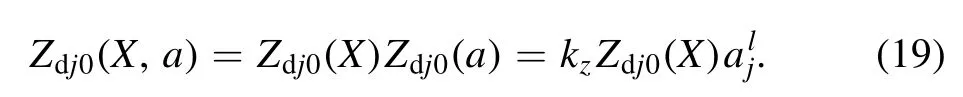
In order to numerically investigate the propagation of shock waves,the following parameters in a typical dusty plasma are obtained from mesospheric plasmas [26,27]:the grain radius a～1 μm,Zd0(0)nd0～0.1ni0(0),electron densityne0(0)～5 × 108cm-3,dust temperatureTd～0.6 eV,ion temperatureTi～1 eV,electron temperatureTe～4 eV,and ion densityni0(0)～109cm-3.For simple calculation,some physical parameters are represented in dimensionless form in the process of theoretical and numerical analysis.The normalized forms ofwcd,amin,σiandnd0areandnd0Ntot,respectively.Assume that the equilibrium ion density decreases exponentially,ni0(X)=where L is the density scale length.When the distribution of ion density is given,the charge on dust particles and the distribution of electron density are calculated by charging current equation at equilibrium and quasi-neutrality equation.

The KdV Burgers equation,equation (9),contains nonlinear and dispersive terms.There are shock waves when the dissipation and dispersion counteract the nonlinear effect in dusty plasmas.In addition,as dissipation is very strong,the shock waves exhibit the monotonic features,however,the shock waves show oscillatory properties when the dissipation is weak.

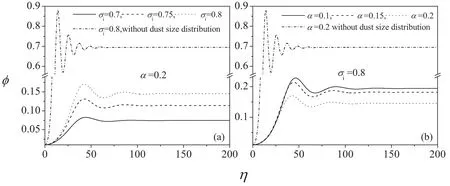
Figure 3.Proflies of shock waves for nd0=0.6,X L=0.8,p=2.8,l=1.2,c=10,amin=0.5,ν=1.2,lx=0.95,wcd=0.2.

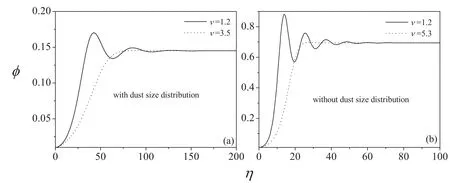
Figure 4.Profiles of shock waves for nd0=0.6,X L=0.8,p=2.8,l=1.2,c=10,amin=0.5,lx=0.95,wcd=0.2,α=0.2,σi=0.8.

Figures 1–4 show the effect of dust size distribution,inhomogeneity,external magnetized field and the oblique propagation on the evolution of shock structures.In order to investigate the effect of the dust size distribution,we have simulated the propagation of shock structures for different values of the pow law index (p),the minimum radius of dust size (amin),the ratio of the maximum and minimum grain radius (c) and the constant (l) depending on dust parameters and other plasma conditions in figure 1.It is found that the oscillation of shock structures strengthens when the ratio of the maximum radius to the minimum radius and the minimum radius of dust size increase,but it weakens with the constant(l).The influence of the power law index on oscillation of shock structures is insignificantly.It is also shown in figure 1 that the strength of shock waves increases withamin,cand p but decreases with l.The dependence of shock structures’features on the inhomogeneity,the oblique propagation,the external magnetized field and the nonthermal ions is illustrated in figures 2 and 3 The effective temperatures (σi) lead to the strengthening of oscillation and strength of shock waves,however,the dust density (n jd0),the position coordinate(X/L),the parameter representing number of nonthermal ions(α),the oblique propagation of shock structures(lz)give rise to the weakening of oscillation and strength of shock structures.So the density of the dust grains increases,the dissipation increases,which is consistent with the experimental result shown in figure 6 of[9].Figure 2(d) illustrates that the oscillation of shock structures decreases withwcd,which means that the external magnetized field acts as a dissipative factor.

Due to the non zero value of ν,the nonlinear dust ion acoustic wave is governed by the KdV Burger equation and the dust ion acoustic shock wave is generated due to the dissipation caused by the nonadiabatic charge variation of the dust particles.Figure 4 shows the dependence of shock structures on the dissipativity related to the variation of charges on dust particles.It is illustrated from figure 4 that the shock waves present an oscillatory shape as ν decreases.When the dispersion parameter is weaker than the dissipative term,oscillations at the front of shock waves occur.However,when dissipation predominates,the shock waves will have a monotonic behavior.The oscillatory shock waves are transformed into the monotone shock waves at ν=3.5 with dust size distribution and ν=5.3 without dust size distribution.Furthermore,it is also shown from figures 2–4 that the oscillation and the strength of shock structures in dusty plasmas with same size of dust grains are larger than that in system with different size of dust grains.That is to say,the nonuniformity of dust particle size will introduce some dissipative factors.

6.Conclusion

The characteristics of shock waves have been explored in nonuniform dusty plasmas containing variational negative charge of dust particles with power law dust size distribution.We analyzed the dependence of characteristic of shock waves on the power law dust size distribution,the inhomogeneity and the nonadiabatic charge variation of dust particles.Numerical simulation shows that there are two kinds of shock waves in the system and when the viscosity parameter leading to the dissipation effect increases the transition from oscillatory shock waves to monotonic shock waves occurs.Additionally,the oscillation and the strength of shock waves in dusty plasmas with same size of dust grains are larger than that in system with different size of dust grains.Through the research in this paper,we can have a deeper comprehension of the characteristics of shock waves in a nonuniform dusty plasma.In different space and astrophysical plasmas,viz.,mesosphere,Saturn’s rings,certain cometary environments,etc,the dust grains have different size.Furthermore,the inhomogeneity is observed from different space plasmas and laboratory discharges.So,the present work might be valid for study space plasmas,for example,mesospheric dusty plasmas with different size dust grains and inhomogeneity.

Acknowledgments

This work was supported by National Natural Foundation of China(No.10975114)and the HongLiu first-class disciplines Development Program of Lanzhou University of Technology.