A novel plasmonic refractive index sensor based on gold/silicon complementary grating structure∗
2021-03-11XiangxianWang王向贤JiankaiZhu朱剑凯YueqiXu徐月奇YunpingQi祁云平LipingZhang张丽萍HuaYang杨华andZaoYi易早
Xiangxian Wang(王向贤), Jiankai Zhu(朱剑凯), Yueqi Xu(徐月奇), Yunping Qi(祁云平),Liping Zhang(张丽萍), Hua Yang(杨华), and Zao Yi(易早)
1School of Science,Lanzhou University of Technology,Lanzhou 730050,China
2College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China
3Joint Laboratory for Extreme Conditions Matter Properties,Southwest University of Science and Technology,Mianyang 621010,China
Keywords: plasmonic sensor,gold,silicon,grating
1. Introduction
In the past few decades, the development of various nanofabrication technologies has provoked the enormous growth of nanostructures in various applications such as photocatalysis,[1–3]absorption enhancements,[4,5]photonic crystals,[6,7]and other fields.[8]Simultaneously, the fabrication of metal micro-nano structures mainly benefits from the rapid growth of electron beam lithography(EBL)and focused ion beam(FIB)milling.The realization of cost-effective metal nanostructures greatly improves the possibilities of their integration in the optical field. When the characteristic size of the metal nanostructure is of sub-wavelength order, a kind of electromagnetic motion mode of light and electron closely combined under the action of external electromagnetic wave,namely surface plasmons,cannot be ignored.[9]In reality,the structures and devices based on surface plasmons make it possible to manipulate and control photons on the nanoscale,which provides a new solution for realizing smaller,faster,and more efficient nanophotonic devices. Moreover, many applications of metal micro-nano structures,such as absorbers,[10]fiber sensors,[11,12]surface-enhanced Raman,[13–15]are all related to the surface plasmons generated by the close interaction between metal nanostructures and incident light.
At present, surface plasmons have a considerable application prospect in the fields of optical sensing, due to their high sensitivity to the physical and chemical properties of the environment, as well as their action range can be controlled at the nano level. In addition, surface plasmons based biochemical sensors are also attracting attention because of their advantages of fast detection speed, high specificity, samplefree labeling,[16,17]and online real-time analysis.[17]However,the plasmonic refractive index (RI) sensors based on prism coupling, which has been successfully commercialized, have gradually exhibited drawbacks in miniaturization and integration owing to its bulky volume. In recent years,the integrated grating coupled plasmonic RI sensors have attracted much attention since it is compatible with the portable development concept of future sensors.[18]Moreover, the noise reduction and light collection are other significant improvement advantages because the grating coupling based plasmonic RI sensors can be excited via normal incidence. Therefore, it is of great significance to design grating coupled plasmonic RI sensor with higher sensitivity,a higher figure of merit(FOM),and a more straightforward manufacturing process(easy to manufacture in a large area)to meet the future needs of RI sensing.
In this work,we propose a novel complementary grating structure for plasmonic RI sensing. Compared with the traditional grating coupled plasmonic RI sensors, our structure can more effectively couple the surface plasmons excited via grating to the environment of the analyte and significantly reduce the full width at half maximum(FWHM),thus improved the FOM. A broadband simulation was performed to extract the structure spectrum characteristics based on TM polarization, and the electric field distributions were obtained using the finite-difference time-domain (FDTD) method. We find that multiple surface plasmon resonance modes can exist in the complementary grating structure. Furthermore,the resonance mode excited via the first-order diffraction coupling of the grating is quite suitable for RI sensing because of its extremely narrow FWHM.The influences of grating geometric variables on resonance behavior are discussed in detail to obtain the appropriate geometric ranges for RI sensing.Finally,the RI sensing performances of the structure are reflected plainly by two important physical parameters,sensitivity and FOM.
2. Structural design
The three-dimensional schematic diagram and the twodimensional profile diagram of the structure are respectively shown in Figs. 1(a) and 1(b). The sensing structure is composed of Si grating,Au grating,and glass substrate. The structure is mainly composed of complementary and directly contacted Si and Au gratings. In essence, it is a functional layer based on the Schottky junction,which is advantageous to current silicon electronic devices from the integration point of view. The analyte is located on the upper surface of the entire structure during the actual RI sensing. Here, the RI of the analyte and the period of the Au/Si grating are assumed to be 1 and 1700 nm, respectively, unless otherwise stated. For the convenience of discussion,grating geometric variables are shown in Fig.1(b),which are the Au grating channel width w,Au grating channel depth td,and the thickness of Si film tsin the Si grating.
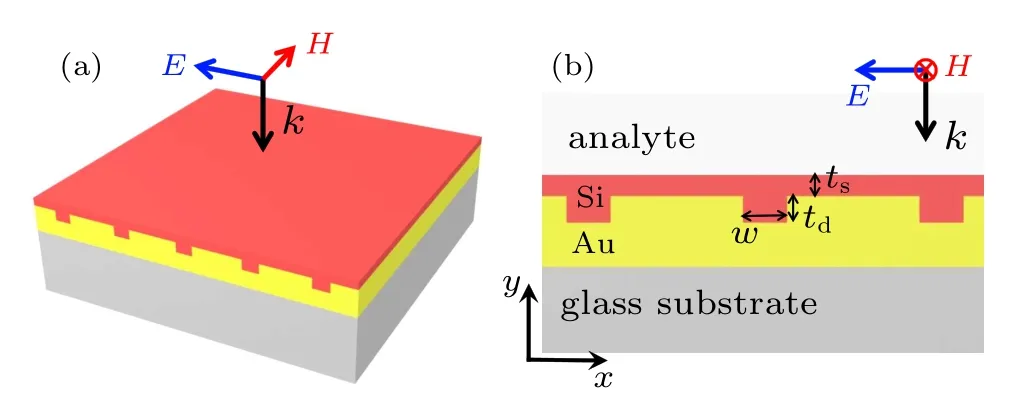
Fig.1. The three-dimensional schematic diagram (a) and the twodimensional profile diagram(b)of the complementary grating structure.From top to bottom are Si grating,Au grating,and glass substrate. The black and blue arrows represent the propagation direction and polarization direction of the incident light,respectively.
As shown by the arrows in Fig.1,this plasmonic structure is excited via vertical incident light with a polarization direction along the periodic direction(TM mode). In the structural design,the purpose of the Au grating is to compensate for the appropriate momentum to excite the surface plasmons propagating along the functional layer composed of complementary gratings. The thickness of the designed Au grating is thick enough; thus,the light transmission of the structure is almost zero in a wide frequency band. The Si grating, complementary to Au grating,has two main objectives. On the one hand,the Si grating makes the contact surface between the analyte and the structure smooth(easy to clean analytes). On the other hand, Si grating can assist Au grating to couple more energy of surface plasmons to the environment of analyte(discussed below). In the numerical simulation, the optical constants of Si and glass substrate (SiO2) are derived from previous experimental values,[19,20]and the dielectric constant of gold is selected from the experimental data supported by the Drude model.[21]
3. Results and discussion
3.1. Plasmonic responses of the structure
The black curve in Fig.2 shows the reflection spectrum of the complementary grating structure in a wide wavelength range of 1400 nm to 4000 nm. Here, the geometric parameters of the complementary grating structure are w=400 nm,td=160 nm, and ts=30 nm, respectively. To illustrate the advantages of the complementary grating structure, we also simulate the reflection spectrum of the structure with only Au grating under the same geometric parameters,as shown in the red curve in Fig.2. It can be clearly seen from the comparison that the complementary grating structure with a layer of Si can excite more surface plasmon resonance modes and can effectively reduce the FWHM of the resonance peak. According to the spectral response of the complementary grating structure,the resonance mode excited at 1708 nm has great advantages in RI sensing due to its strong resonance intensity(reflectivity almost 0)and extremely narrow FWHM(about 5.4 nm). It is worth mentioning that the resonance mode at 3189 nm may have application potential in broadband absorption,benefit by its FWHM of nearly 500 nm.

Fig.2. Reflection spectra of the structures. The black curve shows the reflection spectrum of the complementary grating structure at the geometric variables of w=400 nm,td =160 nm, and ts =30 nm, respectively. The red curve shows the reflection spectrum of the structure with only Au grating under the same geometric parameters.
To intuitively reveal the resonance mechanism caused by grating coupling,we calculated the electric field distributions of the grating coupling structures for each resonance mode(corresponding to Fig.2)in Fig.3. Figure 3(a)shows the electric field distribution at 1813 nm,which is the only plasmonic resonance mode excited via the structure with only Au grating. Figures 3(b)–3(d) show the electric field distributions of the complementary grating structure at resonance wavelengths of 1558 nm, 1708 nm, and 3189 nm, respectively. As can be seen, in the case of Fig.3(a), the electric fields are found to leak into the environment of the analytes, which is the signature of propagating surface plasmon. It can be confirmed that this mode is caused by the first-order diffraction coupling of the Au grating. For Fig.3(c), one can observe a similar phenomenon in the complementary grating structure and draw the same conclusion. Thus, the 1708 nm mode can be illustratively called propagation-mode in the complementary grating structure. However,it can also be observed that the existence of Si grating in complementary grating structure makes the energy of surface plasmons excited by Au grating more evenly coupled to the environment of analytes. Furthermore, the Si grating that flattens the propagation interface of the surface plasmon is the main reason for reducing the FWHM of the first-order diffraction coupled resonance of Au gratings. Remarkably, both these two characteristics caused by complementary gratings are conducive to RI sensing. Subsequently,it can be observed from Fig.3(b) that the weak resonance of Au/Si interface in the channel of Au grating is the reason for the reflection valley at 1558 nm,and a standing wave is formed in the environment of analyte due to the reflection of the incident light. As shown in Fig.3(d),the large capture of the field energy via the Au grating channel is responsible for the resonance mode at 3189 nm,which can be called channel-mode.
To further reveal the role of grating on the excitation of surface plasmon resonances,we theoretically verify the simulation results via the 1D grating equation. Incident light scattering on metal nanostructures results in a wide range of directions for the propagation vector. Then, surface plasmon resonance is generated when the following momentum matching conditions are satisfied:[22]

where k0nsinϕ is the k-vector of the incident light in the xdirection, and 2πm/P is the additional momentum compensated via 1D grating.More specifically,k0=2π/λ is the propagation constant in free space, nais the RI of the analyte, εmis the complex dielectric constant of the gold, ϕ is the incident angle, P is the 1D grating period, m are the diffraction orders of 1D gratings and are integers. In the case of normal incidence,the above equation can be reduced to

where λresrepresents the resonance wavelength.When m=1,the 1708 mode is in good agreement with Eq.(2)obtained via theoretical analysis, which fully testifies that the 1708 mode is excited by the first-order subwavelength diffraction of the grating. The theoretical result is also consistent with the qualitative analysis of the electric field distribution in Fig.3(c).

Fig.3. The electric field distributions of the structures corresponding to each resonance wavelength in Fig.2 and the white dashed line outlined the structures.The electric field distribution of the structure with only Au grating at the resonance wavelength of(a)1813 nm. The electric field distributions of a complementary grating structure at the resonance wavelengths of(b)1558 nm,(c)1708 nm,and(d)3189 nm,respectively.
3.2. Structural optimization
Considering the purpose of using this structure for RI sensing, the following discussion focuses on the 1708 nm mode (propagation-mode), which has strong resonance (low reflectivity)and narrow FWHM,and has extensive interaction with the environment of the analyte. Firstly, the geometric parameters of the structure are optimized, and the geometric parameter tolerance suitable for RI sensing is obtained. Figure 4(a) shows the reflection spectra at the waveband where the propagation-mode is located when w changes from 280 to 680 in a step size of 100 nm with tdand tsfixed at 160 nm and 30 nm, respectively. It can be observed that the resonance wavelengths move towards the shorter wavelength,and the reflectivity decreases first and then increases with the increase of w, while the FWHM presents fluctuation. Hence, a choice of the channel width w of 380 nm(red line)resulted in a decent value of signal contrast. Figure 4(b)shows the reflectivity spectra for w of 380 nm,tsof 30 nm,and variable channel death tdin step size of 20 nm. It can be noticed that the reflectivity decreases to the minimum value and then increases,resulting in an optimal value of 160 nm for td(blue line). Figure 4(c) shows the reflection spectra for w of 380 nm, tdof 160 nm,and with tschanged from 0 nm to 40 nm in step size of 10 nm. It can be observed that with the increase of ts, the resonance wavelength shifts to the long wavelength and is accompanied by the reflectivity gets lower,and the FWHM gradually widened. Here, tsis optimized to be 30 nm (blue line)because there is a trade-off between dip strength and FWHM.

Fig.4. Influences of(a)channel width w,(b)channel depth td,and(c)Si film thickness ts on the 1708 nm mode(propagation-mode).
According to the above discussion,the optimum geometric parameters of the complementary grating structure used for RI sensing are w of 380 nm, tdof 160 nm, and tsof 30 nm,respectively. In addition, two important points can be simultaneously derived from the above discussion on the influence of geometric parameters on propagation-mode: (i)in terms of sensing, this structure is capable of exciting the strong resonances with sensing capability in a wide range of grating variables,which reveals a remarkably high tolerance to geometric parameters of the structure in the fields of RI sensing;(ii)the variations of w, td, and tsshow the minor effect on the peak position of the propagation-mode, this is because the change of the geometric parameters does not alter the essence of Au grating diffraction,and further confirms that the propagationmode at 1708 nm is indeed aroused by grating diffraction after compensating optical momentum.
3.3. The sensing performance of the structure
Based on the above analysis of the plasmonic responses of the complementary grating structure, the sensing performances of the propagation-mode are discussed in detail. Via introducing two crucial physical parameters, sensitivity (S)and figure of merit (FOM), we follow the common knowledge in the field of RI sensing. The RI sensitivity of a plasmonic sensor is generally reported in nanometers of peak shift per refractive index unit (nm/RIU), i.e., S = ∆λ/∆n.The sensing precision depends on higher sensitivity and narrower FWHM;thus,the concept of FOM can be derived,i.e.,FOM=S/FWHM.
Figure 5(a) shows the reflection spectra of the structure under different analyte RI in the waveband where the propagation-mode is located. Here, we assume that the analytes are gases, and their RI varies from 1.0 to 1.1 in step size of 0.02. As shown, the resonance wavelength of the propagation-mode moves to the long-wavelength equidistantly with the even increases of analyte RI.It is also observed that the sensing process is very stable,which is reflected in the fact that the reflectivity and the FWHM of the resonance peaks are almost unchanged.Figure 5(b)shows the relationship between the resonance wavelength and the FOM of the propagationmode with the analyte RI. It is more intuitive to observe that the resonance wavelengths are linearly sensitive to the change of analyte RI.According to the definition of S,the slope of the black line in Fig.5(b)is the value of S and keeps a constant of 1642 nm/RIU.In the range of analyte RI being gas,the FOM is all above 300 RIU−1,and the highest can reach 409 RIU−1.The S of this plasmonic sensor is quite high compared with the RI sensors in recent reports,[23–27]and the FOM is higher than that obtained in other previous studies.[28–31]For Fig.5(a),an interesting phenomenon can also be observed. The mode at about 1558 nm (described in detail in Fig.2) presents insensitive to analyte RI, which indicates the potential application in the RI sensing of self-referenced.[32]The reason can be explained from Fig.3(b), which is the electric field distribution under this mode. One can observe from Fig.3(b)that the region of this weak plasmonic resonance is only confined in the channel of Au grating,and has no effect on the external environment of the analyte.
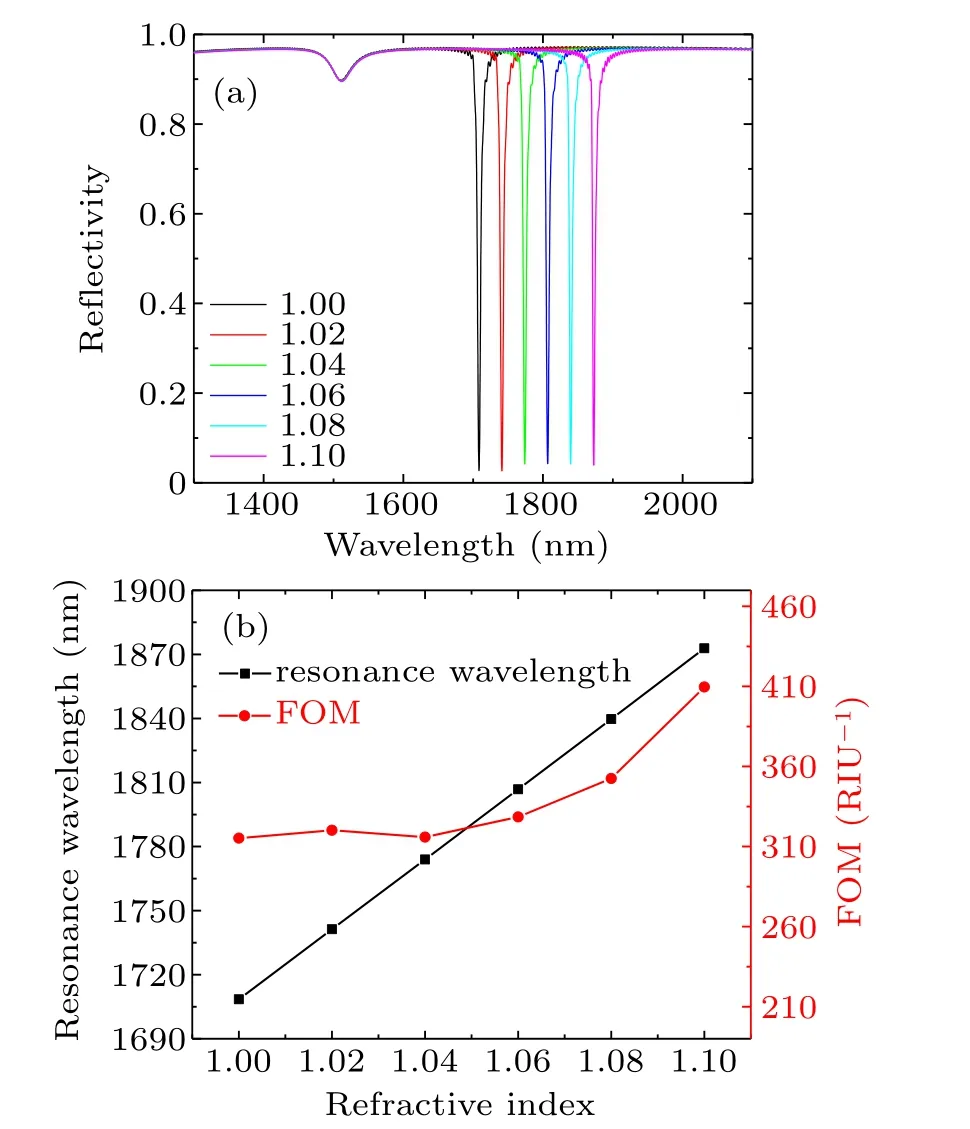
Fig.5. (a) Reflective spectra of the complementary grating structure with the optimum geometric parameters when the analyte RI ranges from 1.0 to 1.1 in steps of 0.02. (b)The relationship of resonance wavelengths and FOM with analyte RI in propagation-mode.
The complementary grating structure we designed can be used not only as a gas RI sensor but also as a liquid RI sensor.Figure 6(a) shows the reflection spectra under the waveband where the propagation-mode is located when the analyte RI varies from 1.3 to 1.4 (within the analyte RI range near liquid). Here,the values of w,td,and tsare the optimized parameters under the grating period equals to 1200 nm. As shown in Fig.6(a), the stable sensing ability of the resonance peak can still be observed, which is shown in the linear sensitivity with the even change of analyte RI and the almost constant FWHM. It is noted that when the structure is used for liquid sensing,the sensing waveband can be the same as that for gas sensing. This is because although the increase of analyte RI will lead to the redshift of the resonance peak,the decrease of the period will lead to the blueshift of that. The flexibility of geometric parameter change is also illustrated when the structure is used for RI sensing. Figure 6(b) shows the sensitivity curve used to calculate S and the relationship between FOM and analyte RI.The sensitivity of the structure used for liquid sensing is estimated to be 1212 nm/RIU,and its FOM is stabilized at about 135 RIU−1. Compared with the structure used in gas sensing, the sensitivity of liquid sensing is obviously reduced. This is due to the decrease of the period,which corresponding to reduce the interaction range between the surface plasmon and the environment of the analyte.

Fig.6. (a) Reflective spectra of the complementary grating structure when the analyte RI ranges from 1.3 to 1.4 in steps of 0.02.Here,the geometric parameters of the structure are with grating period=1200 nm,w=400 nm, td =180 nm, and ts =30 nm. (b) The relationship of resonance wavelength and FOM with analyte RI in propagation-mode.
4. Conclusion
In conclusion, a surface plasmon RI sensor based on a complementary grating structure composed of Au and Si is presented. The effective energy couplings between the surface plasmon and the incident light are fully proved by the detailed discussion of the structure plasmonic responses. A propagation-mode with narrow FWHM and high strength occurs via the first-order diffraction of the complementary grating structure, making it very suitable for RI sensing. After optimizing the geometrical parameters of the structure, the S and the highest FOM of the structure are 1642 nm/RIU and 409 RIU−1,respectively,in the analyte of gas.Moreover,flexible geometric parameters regulation makes the structure can be used for liquid sensing in the same waveband as gas sensing. This plasmonic RI sensor is simple to manufacture and has stable sensing performance in the case of the analytes being gas and liquid. Thus, this sensor can be widely used in biological and chemical RI sensing fields.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Statistical potentials for 3D structure evaluation:From proteins to RNAs∗
- Identification of denatured and normal biological tissues based on compressed sensing and refined composite multi-scale fuzzy entropy during high intensity focused ultrasound treatment∗
- Folding nucleus and unfolding dynamics of protein 2GB1∗
- Quantitative coherence analysis of dual phase grating x-ray interferometry with source grating∗
- An electromagnetic view of relay time in propagation of neural signals∗
- Negative photoconductivity in low-dimensional materials∗
