Comparative analysis of the arc characteristics inside the convergingdiverging and cylindrical plasma torches

Jianghong SUN (孙江宏),Surong SUN (孙素蓉),Haixing WANG (王海兴),Chong NIU (牛冲) and Tao ZHU (朱涛)

School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,People’s Republic of China

Abstract

Keywords:plasma torch,thermodynamic non-equilibrium,arc characteristics

1.Introduction

As an important high temperature heat source,non-transferred arc plasma torch has a wide range of applications in material processing,spraying,biomass gasification and waste disposal.In these applications,the torch performance,such as high enthalpy,good stability,and long service life,especially electrodes life,are of primary concerns for optimal design of plasma torch in making these devices commercially viable[1,2].In spite of significant progresses over the past decades,the physical processes inside plasma torch are still not fully understood.This lack of understanding is a consequence of the complexity prevailing in plasma torch caused by the strongly interactions of electrical,magnetic,thermal,and fluid dynamic effects [3–6].

Traditional direct current (DC) plasma torch has a cylindrical structure as shown in figure 1(a).Over the past several decades,intensive studies have been conducted to investigate the arc behavior in such kinds of torches [7–13].The main advantage of cylindrical torch is that its structure is relatively simple while it also suffers two problems.Firstly,because the essential nature of arc always tends to find the shortest path between the cathode and the anode[14–16],this usually results in a short arc and low arc voltage.Secondly,the gas flow parallels to the anode of cylindrical torch.The arc anode attachment is directly exposed to the action of gas flow and is very susceptible to axial gas dynamic forces.The location of the arc anode attachment is determined by a balance of gas dynamic,electric,and magnetic forces as well as thermal effects [17,18].Under the influence of the superimposed flow the arc attachment at the anode may move upstream or downstream,which leads to that the torch is often operated in a ‘fluctuating mode’ [19–21].The arc root movement inside the torch often relates to the voltage fluctuations and then directly translates into power fluctuations which then affect heating of injected powders in material processing.

Recently,an improved structure of torch with converging-diverging anode is developed which attempts to overcome these disadvantages[22,23].The basic structure of this DC non-transferred arc plasma torch is schematically shown in figure 1(b) which consists of converging section,constrictor and diverging section.It is expected that the converging-diverging torch offers several advantages over cylindrical plasma torch.Firstly,the arc length would be increased due to the presence of the constrictor,and this leads to the increase of arc voltage and thus the input power and enthalpy of plasma jets also increase.Secondly,due to the higher arc voltage,amplitude of the voltage fluctuations becomes small relative to the total arc voltage.Thirdly,it has been found from experiment that in the case of a specific combination of operating parameters,the arc passes through the constrictor and attaches to the expanded section of the anode in a diffusion mode with low current density [24].Although intensive experimental and analytical studies have been carried out for this converging-diverging torch[22,23],the evolution and development of arcs in this kind of torch is still unclear.Since the experimental diagnosis inside the plasma torch is quite difficult,it is necessary to obtain the characteristics of plasma flow in the converging-diverging torch by numerical simulation analysis,especially investigating the effect of the constrictor on the arc characteristics.

The purpose of this paper is to obtain a deep insight into the effect of torch structure on arc characteristics through comparative analysis of the two kinds of plasma torch.In order to avoid specifying the lowest conductivity for conducting current on the anode wall of the plasma torch under local thermal equilibrium (LTE) assumption,a two-temperature thermodynamic non-equilibrium method is used in this numerical simulation.Section 2 presents the physical and mathematic model based on two-temperature chemical equilibrium assumption,the computational domain and boundary conditions.Numerical results of the modeling of the arc behavior inside two kinds of structure plasma torches,including comparisons with experimental measurements,are shown in section 3.Conclusions are drawn in section 4.

2.Modeling approach

2.1.Computation domain

The numerical simulation of this paper is based on two structures of plasma torches.The first is a conventional cylindrical torch which was numerically simulated in [3].In this study,it is used as the baseline torch.As in [3],the simplified structure of cylindrical torch used in the simulation is shown in figure 2(a).It is noted that only the half of the torch geometry is presented since axial symmetry is assumed.The torch has a length of 32 mm (GF) and a radius of 6.35 mm (EF).The cathode is assumed as a cylindrical rod with a radius of 3 mm.The cathode current density is assumed to be uniformly distributed on cathode spot (CD)with a radius of 0.5 mm.For the rest of cathode plane(BC),it is assumed that there is no current flow through this area.The second is a converging-diverging torch which was reported in[22,23].A schematic sketch of the torch is shown in figure 2(b),the length of the torch is 62.82 mm.The inlet JA is 6.65 mm in radius with a length of 2 mm(JI).The converging section(IH)of the torch is 10 mm in length with a half angle of 28°.The diverging section of the anode(FG)is conical with a half-angle of 7°,and the nozzle-exit radius(EF)is 7.1 mm.The constrictor (HG) is 3.22 mm in length and 1.4 mm in radius.The cathode(ABC)is a cylinder rod with a radius of 3.54 mm,with a flat tip (CD) of a radius of 0.5 mm.

2.2.Basic assumptions

The following assumptions are used in this simulation:(1)The plasma is assumed to be axially symmetric,laminar,and steady.(2) The plasma is considered in chemical equilibrium and thermodynamic non-equilibrium,i.e.the electron temperature Teand heavy particle temperature Thcan be different and are separately solved by each energy equation.Maxwellian distributions are assumed for both electrons and heavy particles.(3) Thermodynamic and transport data are determined by Teand Th,which can be calculated by the Chapman–Enskog theory and detailed procedure is described in [25,26].(4) The plasma is assumed to be optically thin,and radiative losses are treated by the net emission coefficient method.(5) Plasma sheath is not included.

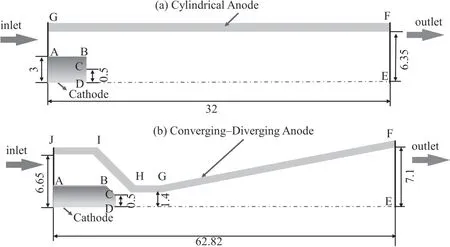
Figure 2.Computational domain of torches with (a) the cylindrical anode and (b) the converging-diverging anode (unit:mm).

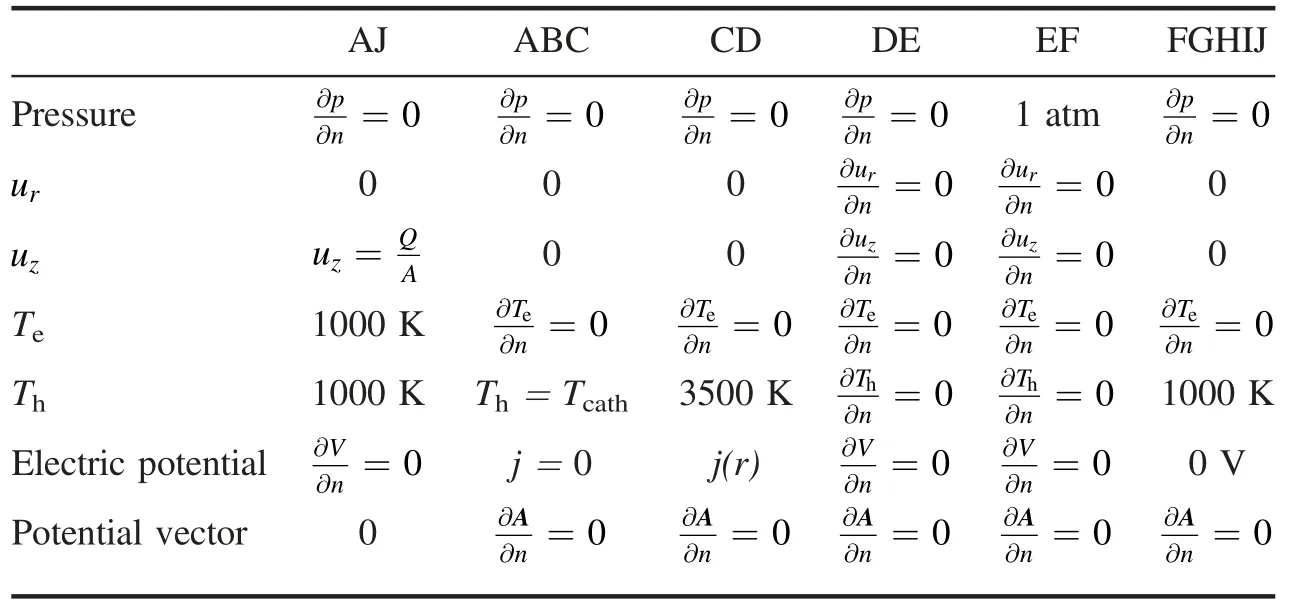
Table 1.Boundary conditions for two-temperature model.

The laminar flow assumption adopted in this simulation is due to the low Reynolds number inside this convergingdiverging torch.According to the geometrical and operating parameters of the plasma torch,the estimated Reynolds number is on the order of 1000.The estimated Reynolds number for cylindrical torch under the flow conditions used in this study is around 200,which is on the same order with the estimation of Westhoff[3].For this condition,the assumption of laminar is reasonable for cylindrical torch.In previous experimental study of plasma torch [22,27,28]the uniform and diffused arc attachments at the anode have been observed with similar operating conditions used in this study.This infers that the arc can be considered as axially symmetric for this case.Although there are small fluctuations in the voltage under the present operational conditions,the measured voltage and electro-thermal efficiency are time averaged and the same input current and gas flow rate are used for simulations.Hence the steady state is assumed in the present model.

It is noted that two-temperature thermodynamic assumption is used in this study.It is because that in the LTE model,the electron temperature is equal to the heavy particle temperature,which is low near the electrodes due to the strong cooling they experience.This causes the low value of the equilibrium electrical conductivity near the electrodes which is not enough to support electrical current flow to the anode.In order to solve this problem,numerical simulation methods based on LTE assumptions usually use various artificial methods to improve conductivity [3,7,8].One of main advantages of two-temperature model is that it does not require any special treatment of the electrical conductivity in cold boundary layer,because the electron temperature will typically remain high in the arc attachment regions.

2.3.Boundary conditions

Figure 3.The predicted temperature distribution (lines) with reported results from [3],I=250 A,Q=9.83 slm.

The boundary conditions for different variables are shown in table 1.The inlet axial velocity is assumed to be constant which is determined by gas flow Q and inlet area A and the radial velocity at inlet is zero.The inlet temperatures for electrons and heavy particles are equal to 1000 K.Zero electron temperature gradient condition is defined in other boundaries.On the axis of symmetry DE,all variables have zero gradient.At the torch outlet,the pressure is set to be 1 atm.For cathode,a linear rising of heavy particles temperature from 1000 K to 3500 K is set along ABC,while at the cathode tip(CD)temperature for the heavy particle is set to be 3500 K.For the sake of comparison,the same constant current density of 3×107A m-2is given at flat tips of cathode for the two torches,which was also used in[3].Zero current density is set on the rest part of the cathode.For the anode boundary,the electric potential is set to be zero.These boundary conditions are typical for plasma torch simulations and the corresponding discussion was presented in detail in[29].For the sake of comparison in the numerical simulation,we use the same gas flow,operating current and cathode tip current density for two kinds of torches.

2.4.Governing equations

The governing equations used in this simulation consist of mass continuity,momentum,electron and heavy particle energy conversation equations and Maxwell equations.The electromagnetic field is closely coupled by the Lorentz force and the Ohmic heating with the momentum equation and the energy equation.Mass continuity:

where ρ represents the mass density and u is the flow velocity Momentum conservation:

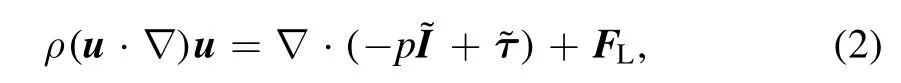
Energy conservation for electrons:

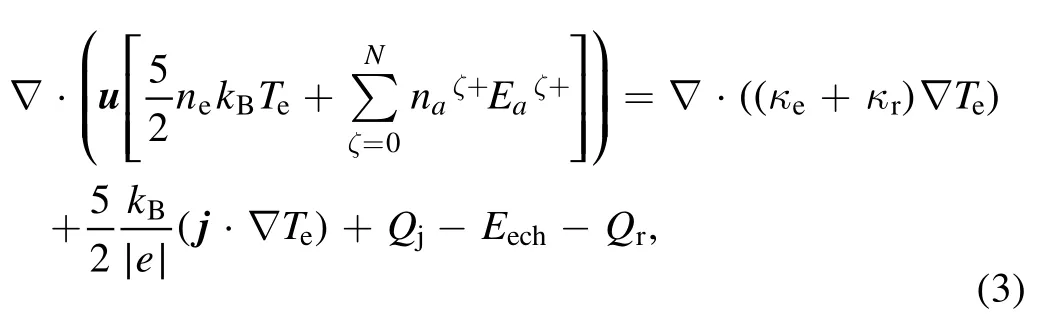
where necorresponds to the electron number density.kBis the Boltzmann constant.represents a particle charged ζ times.represents the ionization energy of this particle,κethe electron conductivity,κrthe reaction thermal conductivity,the enthalpy work of electrons,Qjthe Joule heating,Eechthe electron-heavy-particle energy exchange term,Qrthe volumetric net radiation losses.

Energy conservation for heavy particles:

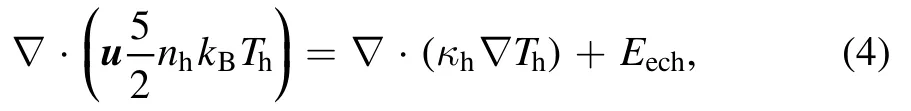
where nhis the heavy particle density,κhthe heavy particle conductivity.

The magnetic vector potential A is obtained from the Poisson equation:

whereμ0denotes the magnetic permeability,j the current density.The magnetic field B which causes the Lorentz force FLcan be derived fromB=∇×A.

Current continuity equation:

Equation (6) together with Ohm’s law (j=σE) and electric potential equation (E=-∇V) are solved,where E is the electric field,σ the electrical conductivity,V the electric potential.

3.Results

3.1.Code validation

The numerical code used in this paper is first used for numerical simulation of the baseline torch to verify the reliability of the code.The cylindrical torch shown in figure 2(a),was previously simulated to investigate the heat transfer,and fluid flow phenomena inside plasma torches by Westhoff’s [3]based on local thermodynamic equilibrium assumption.In order to treat the problem of current conduction in the low temperature region of the anode boundary layer,they adopted an artificially given dependence function of electrical conductivity and temperature below 9000 K.For temperatures above 9000 K the conductivity is equal to the calculated(LTE) values.The arc current and gas flow rate in [3]were respectively set to be 250 A and 9.83 slm.

In order to test our modeling approach,the same geometry,operating parameters of the plasma torch and also based on LTE assumption with[3]are used in this simulation.The comparison between our calculation results of temperature distribution inside plasma torch and the correspondingresults of [3]is shown in figure 3 and comparison of some important typical parameters is given in table 2.As can be seen from figure 3 and table 2,the numerical predictions are in good agreement with Westhoff’s work [3].

In order to further verify the numerical simulation approach used in this paper,the code is extended to simulate the converging-diverging plasma torch based on two-temperature model.Comparison of the predicted axial temperature distribution with the experimental measurement results is shown in figure 4.In the experiment,the converging-diverging torch was operated at arc current of 90 A and argon flow rate of 9.8 slm.Spectral measurement of atomic excitation temperature was conducted with a similar method used in[30].Several 0.9 mm diameter holes were drilled into the diverging section of the plasma torch to provide side-on optical access to the internal flow.Axial distribution of atomic excitation temperature of argon was determined from emission line ratios.As can be seen from the figure 4,the numerical simulation results are consistent with the experimental measurements.It is noted that both the electron and heavy particle temperatures obtained from the two-temperature numerical simulation are plotted in the figure 4,and they are very close to each other,indicating that the plasma is close to the thermodynamic equilibrium along the torch axis.

The measured axial temperatures of mixture of Ar–N2with the converging-diverging torch are presented in figure 5.Similar to the experimental measurement of excitation temperature of pure argon,the axial variation of excitation temperature of argon in Ar–N2mixture was also obtained by relative line intensity ratio method.As can be seen from figure 5 that the addition of nitrogen to the mixture leads to a significant increase in the excitation temperature along the axis of torch.It is mainly due to that adding nitrogen to the mixed gas can significantly increase the specific enthalpy of the gas [31,32].In order to further verify the code,we also performed a numerical simulation using an Ar–N2mixture as the working gas.The calculated axial distribution of excitation temperature of Ar–N2mixture is also presented in figure 5.Considering the uncertainties (～25% [33]) of relative line intensity method used in the experiment,the measured and predicted temperature can be considered to be reasonably agreed.

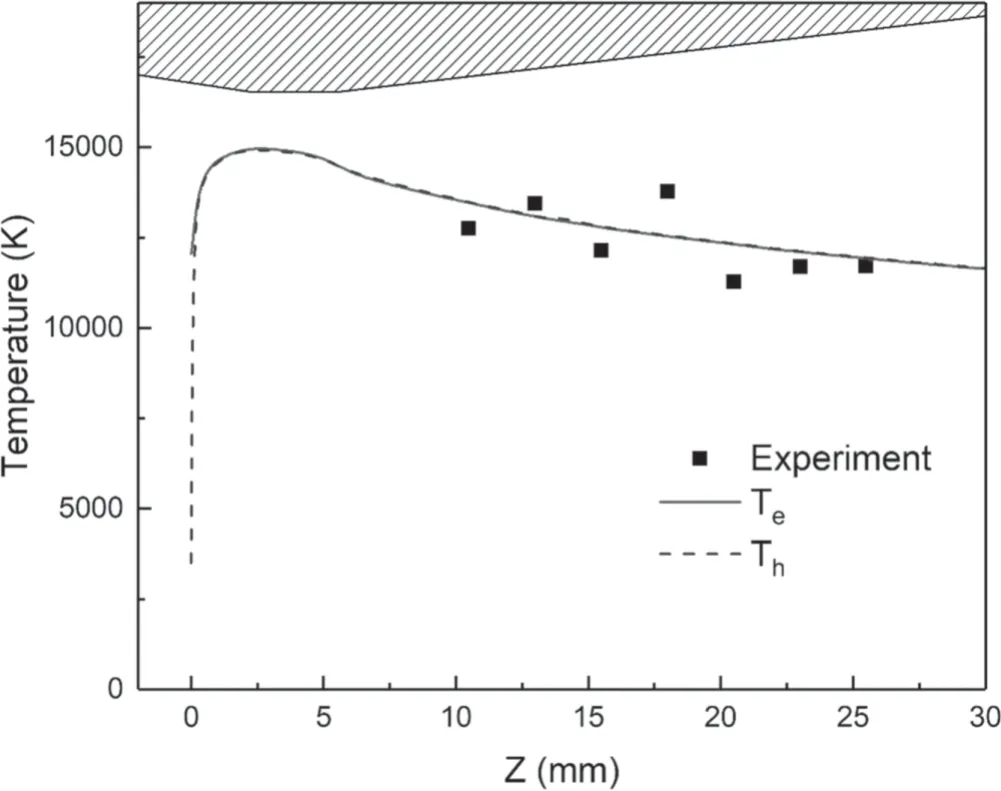
Figure 4.Comparison of the predicted axial temperatures with experimental measurement in the converging-diverging torch(argon,90 A,9.8 slm).

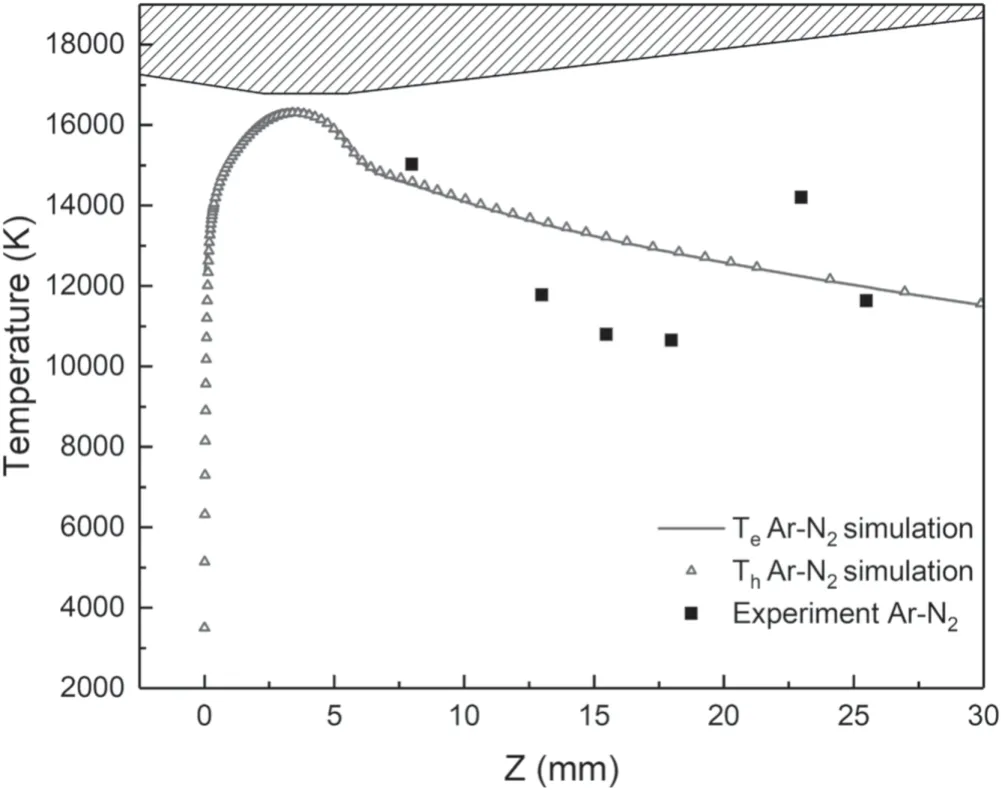
Figure 5.Comparison of the predicted axial temperatures with experimental measurement in the converging-diverging torch (Ar–N2 (65.2% N2),100 A,16.1 slm).

Figures 6 and 7 show the arc attachment conditions on anode surface inside the converging-diverging torch which were taken with digital camera with exposure time of 250 μs and further ICCD pictures also show the same arc root attachment tendency with the exposure time of 5 μs.A specially designed copper mirror with a boron nitride film coated on its surface central-region is employed.The copper mirror was put at the downstream of the torch exit to transmit the upward-view image of the arc plasma torch into the intensified charge coupled device(ICCD)camera[22,24,25].It can be seen from figures 6 and 7 that the arcs are attached to the anode surface in a diffused and uniform mode in the converging-diverging torch for pure argon and even for the mixture of argon and nitrogen.The experimentally observed arc attachment modes demonstrate the reasonability of axisymmetric assumption in the simulation.

Figure 6.The image of the diffused arc attachment for converging-diverging torch with gas flow rates of(a)7,(b)11.2,(c) 14 slm of pure argon,arc current of 80 A.

Figure 7.The image of the diffused arc attachment for converging-diverging torch with the mixture of 2.8 slm argon and 12 slm nitrogen,arc current of (a) 90,(b) 100,(c) 110 A.

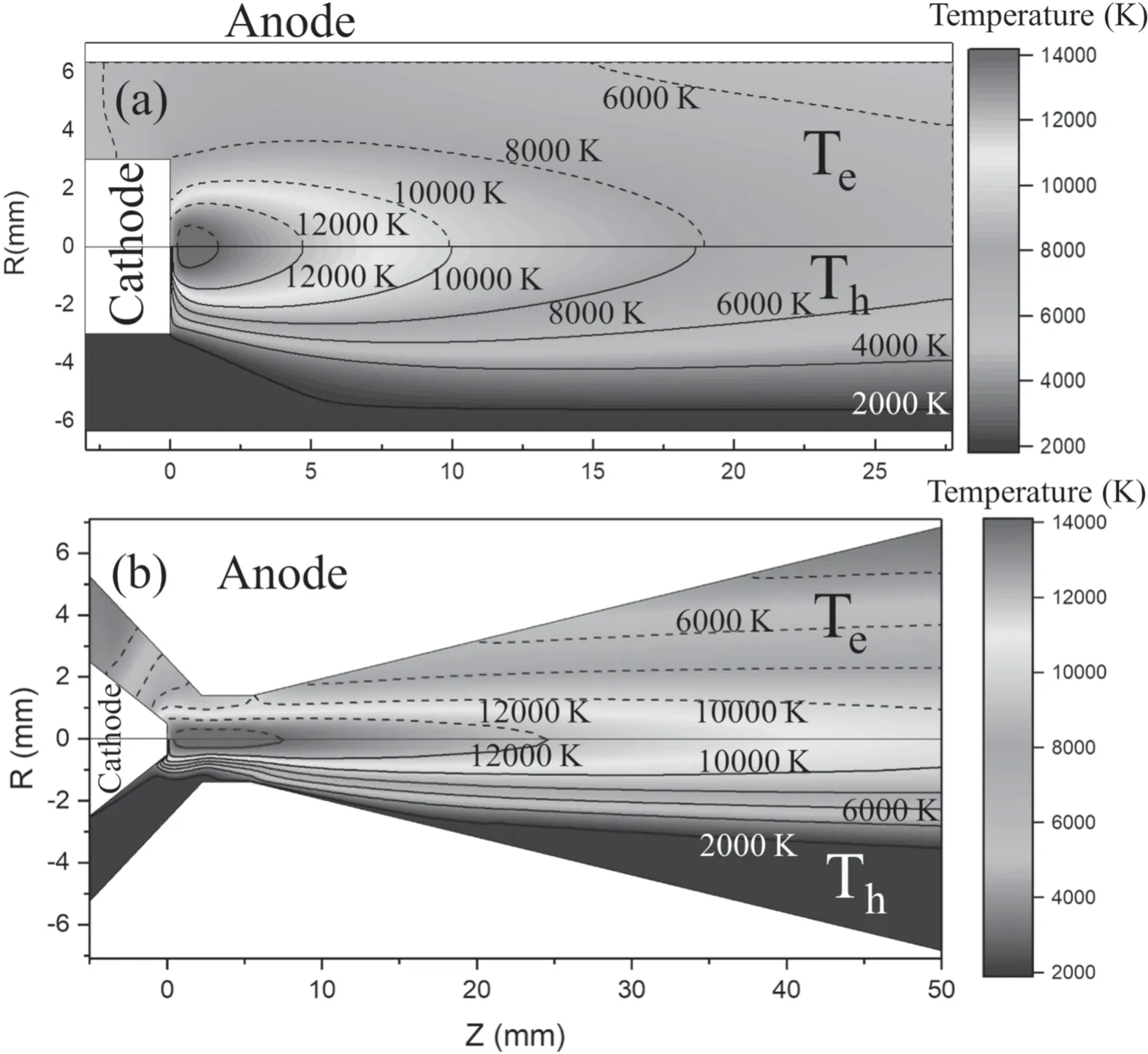
Figure 8.The electron and heavy particle temperature distributions of (a) the cylindrical torch and (b) converging-diverging torch.

Figure 9.Calculated velocity and pressure distributions of the cylindrical torch (a),(b) and converging-diverging torch (c),(d).

3.2.Temperature and flow fields

In order to facilitate comparison,the same operating parameters,arc current of 90 A and gas flow rates of 9.8 slm of pure Ar,are chosen for conventional cylindrical torch and converging-diverging torch in the following simulations.The calculated electron temperature and heavy particle temperature inside the cylindrical torch and converging-diverging torch are given in figure 8.It can be seen that the temperature distributions share two features in common.Firstly,in the central region of the torch,the electron temperature is close to the heavy particle temperature,which infers that the plasma is close to thermodynamic equilibrium state.However,in arc fringes,the electron temperature is higher than the heavy particle temperature,and this indicates that the plasma deviates from the thermodynamic equilibrium state.Secondly,the highest temperatures in the two kinds of torches are almost equal and appear downstream of the cathode tip,indicating that the maximum temperature is primarily determined by the current density distribution of the cathode tip.An important difference between the two temperature distributions is that the length of the high temperature zone in the convergingdiverging torch is much longer than that of cylindrical torch.It is further noted that the length of the converging-diverging torch is approximately 63 mm,which is much larger than 32 mm of the cylindrical torch.It demonstrates that a longer high temperature arc column can be formed inside the converging-diverging torch.The numerical results show that the predicted arc voltage of the converging-diverging torch is 24 V,which is much higher than the 7 V of the cylindrical torch.In the case of the same arc current and gas flow rate,the input power of the converging-diverging torch is much higher than that of the cylindrical torch.

The velocity and pressure distributions in the cylindrical torch and the converging-diverging torch are respectively given in figures 9(a)–(d).It can be seen from the figure 9 that the maximum gas velocity in the converging-diverging torch is 1400 m s-1,which is much higher than 40 m s-1of the cylindrical torch.The main reason for this difference in gas velocities is caused by the pressure difference between the inlet and outlet of the two structural torches.For the converging-diverging torch,the decrease of gas flow cross section area at converging section and the choking effects caused by arc heating inside the constrictor are the main reasons of the increase in the pressure difference between the inlet and outlet of the torch [34].It can be seen that the pressure difference of converging-diverging torch is on the order of 22 000 Pa,while the pressure difference of the cylindrical torch is only around 100 Pa.In the convergingdiverging torch,the higher gas velocity acts to stretch the arc,increase the arc voltage and the power input.

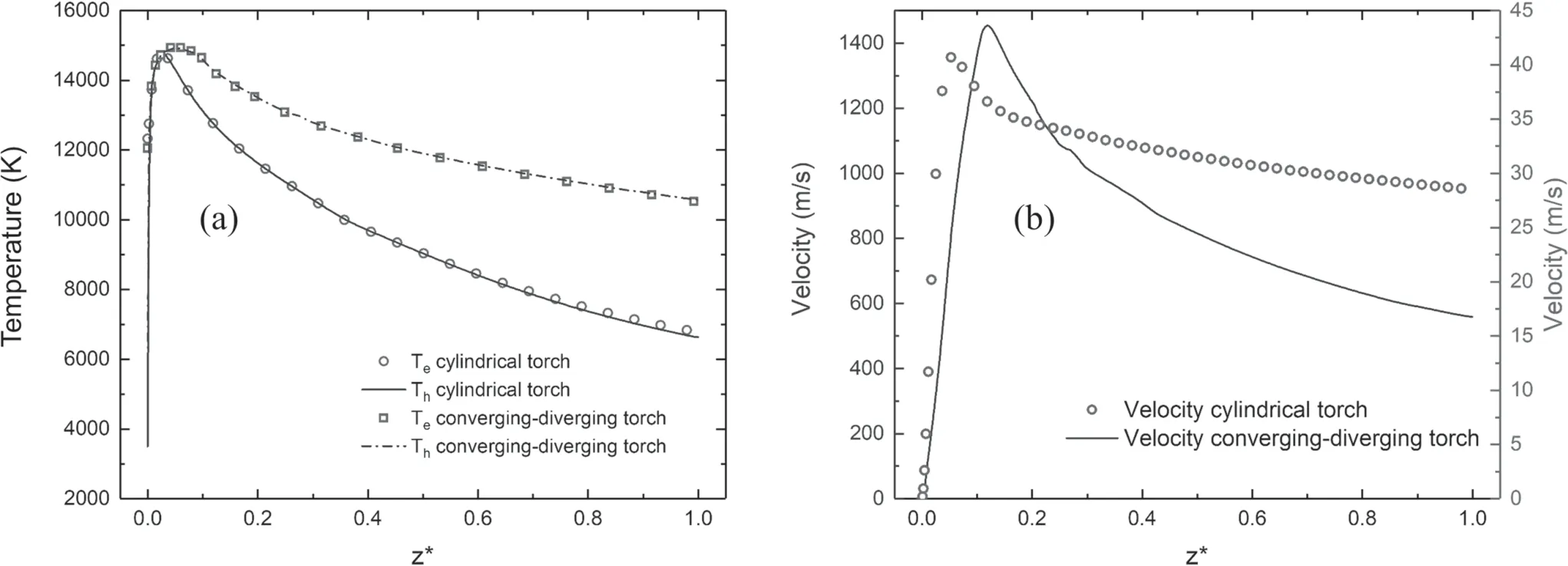
Figure 10.Axial temperature (a) and velocity (b) distributions of two different torches.

Figure 10 shows the velocity distribution and temperature distribution along the axis of the two kinds of torches.It should be noted that in order to facilitate comparison,the axial distances are normalized to their respective length of torch.It is seen that the axial plasma temperature in the convergingdiverging torch decays much slower than that of the cylindrical torch even though the actual length of the converging-diverging torch is much longer.As can be seen from figure 10(b),the positions at which the highest speeds appear inside the two kinds of torches are different.For cylindrical torch,the maximum of gas velocity occurs near the downstream of the cathode tip,which is primarily driven by j×B pumping effect(j is the current density and B the magnetic induction due to the arc current) in the vicinity of the cathode.However,the maximal velocity inside converging-diverging torch appears around the exit of constrictor.It is because that the gas flow in the constrictor is still subsonic,arc heating continues to accelerate the gas,reaching a maximum at the beginning of the diverging section of the torch.The predicted highest Mach number of approximately 0.56 also appears near the exit of the constrictor infers that the flow velocity in diverging-converging torch is lower than the speed of sound.Since the plasma torch is operated at a back pressure of 1 atm,the gas cannot be fully expanded in the diverging section of the torch unlike the arcjet thruster operated under vacuum conditions[35–41],so both the gas velocity and the Mach number in the diverging section of the torch decrease as the axial distance increases.

3.3.Arc characteristics

For the converging-diverging torch,the evolution and development of the arc between the cathode tip and the constrictor exit are critical,so comparison and analysis of arc characteristics of the two kinds of torches are focused in this region.Figure 11 presents the radial distribution of electron,heavy particle temperature and degree of thermodynamic non-equilibrium(Te/Th)at the axial distance 0.5,2 and 6 mm downstream of cathode tip,which corresponds to axial position of the near cathode,the inlet and the outlet of constrictor for the converging-diverging torch.It is noted here that in order to facilitate comparison the radial distances are also normalized according to the respective arc channel radius.

As can be seen from the figures 11(a) and (c),for the cylindrical torch,the thermodynamic equilibrium area of the arc occupies a small proportion of the channel of torch,which is about 0.3 of the dimensionless radius.In most of the radial region of the torch channel,the plasma deviates significantly from the thermodynamic equilibrium state.As the axial distance increases from 0.2 to 6 mm,the variation of arc column diameter is small since the channel diameter does not change.

For the converging-diverging torch,the evolution characteristics of the arc before and after the constrictor are different from that of cylindrical torch.It can be seen from the figures 11(b)and(d),as the axial distance increases from 0.2 to 6 mm,the heavy particles and electron temperatures increase across the entire section of channel.It is shown by the dot–dash lines in figures 11(a) and (b),if we define a heavy particles temperature of 6000 K as the boundary of the arc column [34],for the cylindrical torch,the dimensionless radius of the arc column increases from 0.4 to 0.55.However,for the converging-diverging torch the dimensionless radius of the arc column increases significantly,which increases from 0.4 to 0.75.On the other hand,the dimensionless radial thermodynamic equilibrium region of the arc within the converging-diverging torch is also significantly increased relative to that of the cylindrical torch.Similar phenomenon has also been found in the numerical simulation of an arcjet thruster with a converging-diverging nozzle [34]that the radius of the arc core in the constrictor also increases with increasing distance.It can be seen from figure 2 that the radius of the constrictor is only 1.4 mm,which is much smaller than 6.35 mm,the channel radius of the cylindrical torch.The gas is compressed in the constrictor due to the limitation of cold wall,which enhances the mixing of the low temperature gas around the arc column and the high temperature core region.This increases the average temperature of the gas across the constrictor section and improves the degree of thermodynamic equilibrium of the plasma.

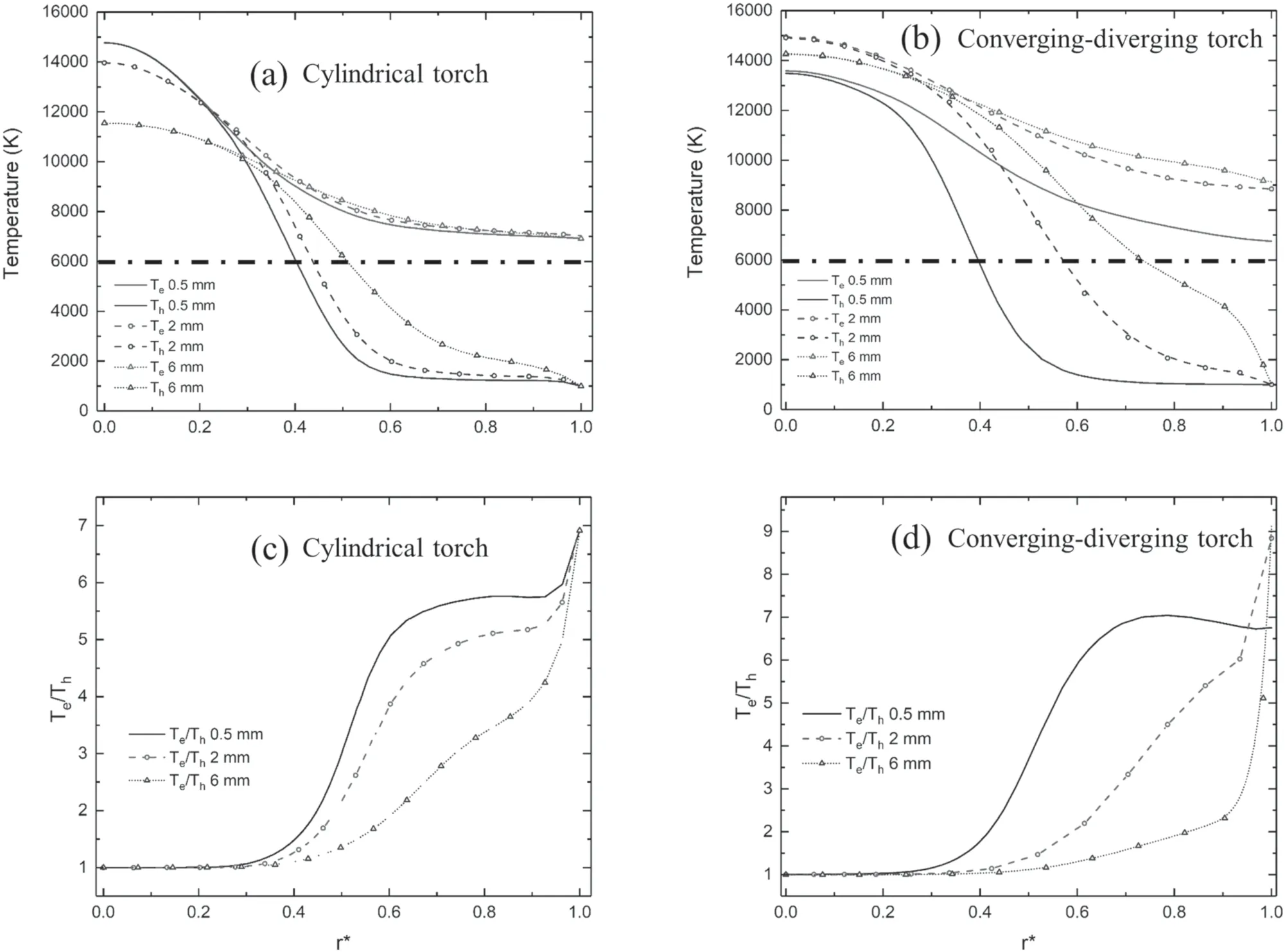
Figure 11.Normalized radial distribution of Te,Th(a),(b)and the non-equilibrium temperature ratio(c),(d)at different distances away from the cathode tip for the cylindrical (a),(c) and converging-diverging torch (b),(d).

3.4.Analysis of radial momentum balance

The evolution and development of plasma arc in the torch are determined by the interaction of different forces.Therefore,analyzing the radial distribution of different forces in the developing stage of the arc can deepen our understanding of the influence of torch structure on the arc characteristics[42].Figure 12 presents the normalized radial profiles of different forces acting on the arcs for two kinds of torches.It can be seen from figures 12(a)–(c),for the cylindrical torch,the forces that dominate the radial evolution of the arc are radial gas dynamic forces and Lorentz forces which are in the opposite direction.With the increase of the axial distance from 0.2 to 6 mm,the radial pressure gradient and arc current density decrease with the arc development.This results in the decrease of peak values of radial gas dynamics force and Lorentz force.

The radial evolution of forces in the converging-diverging torch is significantly different from that in the cylindrical torch.At the downstream of cathode tip,i.e.axial distance of 0.5 mm,the radial gas dynamic force is mainly balanced with the Lorentz force when the dimensionless radius is small,i.e.corresponding to the arc column region.While for the region with dimensionless radius larger than 0.3,the radial gas dynamic force becomes negative which also acts as to compress gas.This is due to the fact that in the converging section of the torch,most of the gas has to pass through the low temperature gas region in arc fringes,thereby increasing the gas pressure gradient in this region and creating a large radial force pointing to arc center.At the inlet of constrictor,i.e.axial distance of 2 mm,the radial gas dynamic and Lorentz force forces are still balanced in the arc column region.In the arc fringes,the radius of the converging section decreases to the radius of constrictor and this leads to the significant increase of the radial gas dynamic force that points to arc center.This radial gas dynamic forces directing toward the arc center in the converging section and the constrictor serve to enhance the mixing of the gas in the high temperature zone of the arc column with the gas in the cold boundary layer.At the axial distance of 6 mm,i.e.the exit of constrictor and also the upstream of diverging section of the torch,the dominant force is the gas dynamic force that causes the arc to expand radially,and the Lorentz force is almost negligible due to the decrease in current density.This facilitates the arc attachment to the anode in this area.

The experimental observation of arc root attachment for this converging-diverging torch was reported in [22].The pictures recorded by ICCD camera show that in most situations the mixture of nitrogen–argon arc attaches at the downstream of constrictor,i.e.upstream of diverging section of torch.The experimentally observed arc attachment area is qualitatively consistent with this numerical simulation results.It should be mentioned,however,that it is very difficult to accurately predict the location and area of the arc attachment at anode.Arc attachment not only depends on the evolution of radial forces but also on the balance of axial gas dynamic forces and Lorentz forces at the arc attachment region.In arc attachment region,the plasma deviates from both the thermodynamic and chemical equilibrium simultaneously,making the prediction of current density distribution very difficult.There is a need to develop a reasonable model to describe chemical non-equilibrium and species transport process that can accurately capture arc fringe characteristics.

4.Conclusions

Arc characteristics inside the conventional cylindrical torch and converging-diverging torch are investigated in this study.In order to avoid the use of artificially given conductivity near the surface of the anode,a two-temperature model is used in the numerical simulation.The reliability of the code is verified by comparing the predicted results with the numerical simulation results of the baseline torch and with the measured axial distribution of temperature in the converging-diverging torch.

It is found that that due to the presence of the constrictor,the arc characteristics in the converging-diverging torch are quite different from those in the cylindrical torch.In the converging-diverging torch,the pressure difference between the inlet and outlet is much larger than that of cylindrical torch due to the reduction of the flow cross-sectional area and the thermal choking effects of arc heating inside constrictor.Therefore a much higher plasma flow velocity and relatively longer high temperature region can be generated and maintained inside the converging-diverging torch.Correspondingly,the higher gas velocity acts to stretch the arc,increase the arc voltage and the power input.

The other important role of the constrictor is to enhance the mixing of high temperature gas in the arc column and the low temperature gas in the boundary layer,and to increase the average temperature of the channel section.The modeling results show that in the constrictor,the radius of the arc column increases with the increase of the axial distance,and the thermodynamic equilibrium degree is also improved.This corresponds to the decrease of thickness of the cold boundary layer in the constrictor,which is beneficial to the arc attaching to the anode in the diverging section.

The momentum balance analysis before and after the constrictor allows us to have a deeper understanding of the evolution process of the arc.For converging section of torch,from the downstream of the cathode tip to the inlet of the constrictor,there exists a strong radial gas dynamic force which points to arc center.At the exit of constrictor and also the diverging section of the torch,the dominant force is the aerodynamic force that causes the arc to expand radially and this is also very beneficial for the arc attaching to this area with diffusive mode.

Acknowledgments

This work was supported by National Natural Science Foundation of China (Nos.11575273,11735004,11575019)and the National Postdoctoral Program for Innovative Talents(BX20180029).The authors especially thank Pan Wenxia for providing the experimental data and photos.