Extremely hidden multi-stability in a class of two-dimensional maps with a cosine memristor

Li-Ping Zhang(张丽萍) Yang Liu(刘洋) Zhou-Chao Wei(魏周超) Hai-Bo Jiang(姜海波)Wei-Peng Lyu(吕伟鹏) and Qin-Sheng Bi(毕勤胜)

1Faculty of Civil Engineering and Mechanics,Jiangsu University,Zhenjiang 212013,China

2School of Mathematics and Statistics,Yancheng Teachers University,Yancheng 224002,China

3Engineering Department,Mathematics and Physical Sciences,University of Exeter,Exeter EX4 4QF,UK

4School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China

Keywords: two-dimensional maps,memristive maps,hidden attractors,bifurcation analysis,extremely hidden multi-stability

1. Introduction

Since memristor was regarded as a fourth circuit component by Chua in 1971[1]and physically implemented by HP laboratory in 2008,[2]it has been intensively studied in the literature and extensively applied in many fields.[3]Very recently, discrete memristor has begun to receive many researchers’ attention.[4–20]For instance, Penget al.presented a model of discrete memristor via the difference theory and derived a memristive H´enon map in Ref.[4]. Then they gave a higher-dimensional map containing the discrete memristor and studied the dynamical behaviors of the map in Ref.[5]. Meanwhile, Baoet al.constructed a two-dimensional (2D) memristive map based on the method of sampling and showed the chaotic and hyper-chaotic behaviors of the map in Ref. [6].Liet al.provided several examples of 2D memristive maps and investigated complex dynamics by considering their coupling strengths and initial values in Ref.[7].In Ref.[8],Baoet al.gave four representations of the discrete memristor model and studied the complex behaviors of their corresponding 2D memristive maps. Baoet al.proposed a memristive Logistic map and investigated the dynamical behaviors of the proposed map in Ref. [9]. In Ref. [10], Baoet al.presented a class of three-dimensional (3D) memristive maps and studied the application of these maps. Liet al.investigated the effect of magnetic induction on the constructed memristive Rulkov neuron map in Ref. [11]. In Ref. [12], Deng and Li established a class of 2D non-autonomous memristive maps that can display hyper-chaotic, periodic, and bursting oscillations. Deng and Li yielded a memristive sine map and studied non-parametric bifurcation and hyper-chaotic behaviors of the map in Ref. [13]. In Ref. [14], Konget al.put forward a 2D memristive map by introducing a discrete sinusoidal memristor. Liu gave and investigated a memristive map by couping the discrete memristor with nonlinear maps of sine and cosine functions in Ref. [15]. In Ref. [16], Liet al.presented a memristor-type chaotic mapping whose parameters could be considered as partial and total amplitude controllers. Fuet al.constructed a class of discrete quadratic memristors and implemented the memristor by using Simulink in Ref. [17]. In Ref. [18], Maet al.put forward a memristive hyper-chaotic map by introducing the proposed discrete memristor into a class of 2D generalized square maps. Ramakrishnan proposed a new memristive neuron map and investigated the complex dynamics of the networked maps by hybrid electrical and chemical synapses in Ref.[19]. In Ref.[20],Lai and Lai presented a 2D memristive hyper-chaotic map with a line of fixed points by coupling a discrete memristor into an enhanced Logistic map. Laiet al.proposed a memristive neuron map by introducing a discrete memristor into an existing neuron map in Ref.[21]. In Ref.[22],Ronget al.constructed a 3D memristive map by coupling a discrete tangent memristor to the H´enon map. Penget al.gave three 2D memristive sine maps by introducing three discrete memristor models into the sine map in Ref.[23]. In Ref.[24],Baoet al.presented a 2D memristive map by implementing sine transformation for the memristor. The memristive maps proposed in Refs.[4–24]usually have several fixed points or a line of fixed points.

If the map has no fixed points,the map belongs to the category of maps with hidden attractors according to the classification of self-excited and hidden attractors given by Leonov and Kuznetsov.[25–27]The basin of attraction of the attractor does not contain any small neighborhoods of fixed points of the map, so it is called a hidden attractor. Otherwise, if the basin of attraction of the attractor intersects with small neighborhoods of any fixed points of the map, it is called a selfexcited attractor.[28]Hidden attractors are difficult to be located and may lead to unexpected responses, so the hidden attractors of continuous and discrete-time systems have been extensively investigated in the literature.[29–33]In Ref. [34],Ramadosset al.obtained several memristive maps without any fixed points by introducing a tiny perturbation and showed hidden attractors in these maps. If a dynamical system generates more than one attractor for a set of fixed parameters using different initial conditions, the system has multi-stability. If the number of the coexisting attractors of the dynamical system for a set of fixed parameters and different initial conditions is infinite, this phenomenon is called extreme multi-stability.Multi-stability and extreme multi-stability of dynamical systems have been found in many disciplines,including physics,chemistry, biology, and economics.[35,36]Very recently, extreme multi-stability of nonlinear maps has received much attention.[37–40]In Ref.[37],Zhanget al.presented a class of 2D chaotic maps with extreme multi-stability by introducing a sine term. Baoet al.proposed a 2D hyper-chaotic map with extreme multi-stability in Ref.[38]. In Ref.[39], Konget al.proposed a 2D hyper-chaotic map with conditional symmetry and attractor growth by introducing two sine terms. Liet al.constructed a 2D map with a sine function to show the selfreproducing dynamics of the map,i.e., reproducing infinitely many coexisting attractors of the same structure but in a different position in Ref.[40].

If a nonlinear map exhibits coexisting hidden attractors(or infinitely many coexisting hidden attractors), we say the map has hidden multi-stability (or extremely hidden multistability). When the map generates infinitely many coexisting hidden attractors having the same shape but different amplitudes, frequencies, or positions, the map has homogenous extreme hidden multi-stability. While the map has infinitely many coexisting hidden attractors of different types, the map has heterogeneous extreme multi-stability. In Ref. [41], Zhanget al.formulated a class of 2D rational maps showing hidden attractors and hidden multi-stability.Then Zhanget al.studied hidden attractors and hidden multistability of a class of 2D rational memristive maps without fixed points in Ref. [42]. However, to the best of our knowledge, the work on memristive maps with extremely hidden multi-stability is limited, which motivates the present study.The main novelties and contributions of this paper are as follows: (i)A new class of 2D maps with a cosine memristor is presented to show extremely hidden multi-stability. (ii) The nonlinear dynamics of the memristive map is numerically analyzed by using several numerical tools including phase portraits, basins of attraction, bifurcation diagram, and the Lyapunov exponent spectrums(Les). (iii)The two-parameter bifurcation analysis of the memristive map in the regions concerned has been carried out to reveal the bifurcation mechanism of the nonlinear dynamics. (iv)The memristive map can display different types of infinitely many coexisting attractors.

The rest of this paper is organized as follows. In Section 2, we formulate the mathematical model of this class of 2D maps with a cosine memristor and study the existence of their fixed points. In Section 3,we investigate the rich dynamics of the memristive map by using numerical analysis tools.Finally,we draw conclusions in Section 4.

2. System model

The equation of the cosine memristor[7]is given by

wherevk,ik, andqk(k=0,1,2,...) denote the output, input,and internal state of the cosine memristor at stepk, respectively.M(qk)=c(cos(dqk))represents the memristance of the cosine memristor.

In this paper,the discrete cosine memristor is coupled to a one-dimensional constant map,and a class of 2D memristive maps is formulated as

wherexkandyk(k=0,1,2,...)are the states at stepk,the coefficientsa,b,c,d,andeare the parameters. In this paper,we assume that the parameters are all not equal to zero,i.e., the map contains the constant term and the cosine memristor.

Remark 1 In Ref.[7],if the parametersc,d,andeof the cosine memristor are chosen as(c,d,e)=(1,1,1),“8”-shaped tight hysteresis loop and the characteristic of the fingerprint and memory can be shown in the cosine memristor.

Remark 2 In Ref. [34], the constantawas considered as a tiny perturbation,i.e.,a=0.001 and only the dynamics of the memristive map with fixed parameters was shown. In this paper,the parameterawill be taken as a varying parameter,and the extremely hidden multi-stability of the memristive map with a cosine memristor will be demonstrated.

One can get the fixed points (x*,y*) of the memristive map(2)by solving the following equations:

Sincea/=0, there is no solution in Eq.(4), so the memristive map (2) has no fixed points. Then the mathematical model of the memristive map with no fixed points is formulated,which is scarcely seen in the memristive map. Since the memristive map(2)has no fixed points,the basin of the attractors in the memristive maps does not contain any fixed points.According to Definition 1 given in Ref.[28],the attractors of the memristive map(2)are all hidden.

By the translational symmetry,i.e.,S(x,y+2mπ) =S(x,y), whereS(x,y) = (a+b(c(cos(dy)))x-x,ex),m=1,2,..., the memristive map(2)may produce infinitely many coexisting hidden attractors having the same shape but in different positions.So the map may display homogenous extreme hidden multi-stability, which is rarely studied in the memristive maps before.

3. Complex dynamics of the 2D map with a cosine memristor

In this section, the complex dynamics of the memristive map (2) will be explored by utilizing numerical analysis tools. The Lyapunov exponent spectrums of the attractors of the memristive map (2) will be calculated by using the Wolf methods.[44,45]The iteration length of the memristive map(2)is chosen as 105.

3.1. Dynamical region

Figure 1 presents a two-parameter dynamical region of the memristive map(2), which can show the effect of the parametersaandbon the dynamics of the map.The period of the periodic solutions and Lyapunov exponent spectrums(Les)of other solutions were used to determine the dynamical regions.Denote the largest Lyapunov exponent and the smallest Lyapunov exponent by Le1 and Le2,respectively.The memristive map(2)is in hyper-chaotic state if Le1＞Le2＞0. The map is in chaotic state if Le1＞0 and Le2＜0. The map is in quasiperiodic state if Le1=0 and Le2＜0. The map is in periodic state if Le1＜0. We run the compute program in parallel for the parametera. In each parallel,we fix the parametera,and vary the parameterbin the interval [-3,3]. The initial states were selected randomly in the region{(x,y)|x,y ∈[-15,15]}if there is no steady attractor.We use the last state of the steady attractor for the initial state for the next step of the parameterb.In Fig. 1, the regions of different dynamical behaviors are marked with different colors, where the regions of period-2 to period-16 solutions are shown in different colors labeled by the numbers ‘2’ to ‘16’, and the region of periodic solutions whose period is more than 16 is indicated in the gray color labeled by ‘M’. And the regions of quasi-periodic (T),chaotic(C),hyper-chaotic(H),and divergent(D)solutions are denoted by the light blue,black,dark black,and white colors,respectively. From Fig.1,we can observe complex dynamics,including hidden periodic,quasi-periodic,chaotic,and hyperchaotic solutions. Moreover,the cascades of period-doubling bifurcations of the memristive map(2)are seen clearly. Note that the dynamical regions are symmetric about the horizontal linea=0 and the vertical lineb=0.

Fig.1. The two-parameter dynamical regions of the memristive map(2)calculated for a ∈[-3,3], b ∈[-3,3], and(c,d,e)=(1,1,1). Different colors labeled by the numbers‘2’to‘16’represent period-2 to period-16 solutions.The gray color labeled by‘M’indicates the periodic solutions whose period is more than 16. The light blue, black, dark black, and white colors denote the quasi-periodic(T),chaotic(C),hyper-chaotic(H),and divergent(D)solutions,respectively.

Fig.2. The two-parameter bifurcation curves of the memristive map(2)calculated for a ∈[-0.7,0.7], b ∈[-0.95,1.75], and (c,d,e)=(1,1,1). The two-parameter bifurcation curves are denoted by different color lines,where PDi represents the period-doubling bifurcation of period-i solution, LPi indicates the saddle-node bifurcation of period-i solution, i=2,4,8. LPPD denotes the codimension-2 bifurcation point, which is the intersection of saddle-node bifurcation and period-doubling bifurcation.

To show the bifurcation mechanism of dynamical transition of the memristive map(2),the two-parameter bifurcation analysis are carried out fora ∈[-0.7,0.7],b ∈[-0.95,1.75]and(c,d,e)=(1,1,1). Figure 2 presents several two-parameter bifurcation curves of main low-periodic solutions. Different color lines are used to denote the two-parameter bifurcation curves,where the period-doubling bifurcation of period-isolution is represented by PDi,the saddle-node bifurcation of period-isolution is indicated by LPi,i=2,4,8. The intersection of saddle-node bifurcation and period-doubling bifurcation is labeled by LPPD,which is a codimension-2 bifurcation point.

3.2. The bifurcation analysis of parameter a

The one-parameter bifurcation diagram can be classified into three categories,i.e., bifurcation diagram using random initial values, bifurcation diagram using a fixed initial value,and bifurcation diagram using the last state of the steady solutions. The bifurcation diagram using random initial values can be called a random bifurcation diagram. Many initial values are selected randomly in an interval for each bifurcation parameter value in the random bifurcation diagram. So the interval where the initial values are randomly taken from has a certain influence on the bifurcation diagram. The random bifurcation diagram may exhibit all possible attractors if the interval is chosen appropriately. To show the phenomena of extreme homogenous hidden multi-stability, we adopted the random bifurcation diagrams of the memristive map(2)by selecting its initial values randomly in an interval.

3.2.1. The case: b=1.6

Fig.3. Random bifurcation diagrams of(a)x, (b)y(y ∈[-12,12]), and(c)Lyapunov exponents spectrum (Les) of the memristive map (2) calculated for a ∈[-0.7,0.7]and(b,c,d,e)=(1.6,1,1,1). The black dots represent the states of the attractors. The red and blue dots indicate the largest Lyapunov exponent(Le1)and the smallest Lyapunov exponent(Le2),respectively. The horizontal dashed line denotes the zero value of the Lyapunov exponents.

Figure 3 depicts random bifurcation diagrams and Lyapunov exponent spectrum (Les) diagram of the memristive map(2)with the parameter(b,c,d,e)=(1.6,1,1,1),whereawas used as a bifurcation parameter,and the initial states were randomly chosen in[-15,15].In Figs.3(a)and 3(b),the states of the attractors are denoted by black dots. In Fig. 3(c), the largest Lyapunov exponent (Le1) and the smallest Lyapunov exponent (Le2) are indicated by red and blue dots, respectively. Since there are infinitely many coexisting attractors,the range ofyis set asy ∈[-12,12]in Fig.3(b). From Fig.3,we can show the influence of the parameteraon the hidden dynamics of the memristive map (2) and a good agreement between the Lyapunov exponent diagram and the bifurcation diagram.Figure 4 presents the phase portraits of the coexisting solutions for the memristive map(2). Since there are infinitely many coexisting attractors, we only gave the phase portraits in the region{(x,y)|x ∈[-2.5,2.5],y ∈[-12,12]}. Whena=0, two different cases of hidden period-2 solutions coexist. Since the memristive map (2) is invariant for the transformation (x,y,a,b,c,d,e)→(-x,y,-a,b,c,d,e), the bifurcation diagram shows symmetrical about the diagonal line. So we only consider the case thata ＞0. From Fig. 3, when 0＜a ＜0.015, the memristive map (2) shows two different cases of hidden period-2 solution (Fig. 4(a)). Asaincreases to 0.015, one case of hidden period-2 solutions disappears. Ata=0.192, the memristive map (2) encounters a period-doubling bifurcation,and the hidden period-4 solutions(Fig. 4(b)) bifurcate to hidden period-8 solutions (Fig. 4(c)).Whena=0.265,another period-doubling bifurcation occurs,converting these hidden period-8 solutions into hidden period-16 solutions. Then these hidden period-16 solutions become multiple-piece chaos(Figs.4(d)and 4(e))via a perioddoubling bifurcation cascade. Hereafter, we can observe a small window of hidden periodic solutions(Fig.4(f)),and the memristive map(2)goes into chaotic states(Fig.4(g))again.After that,we can observe another small window of hidden periodic solutions(Fig.4(h)). Then the memristive map(2)enters into chaotic states(Fig.4(i)). Whena=0.667,the memristive map(2)displays a two-piece chaotic attractor.Based on our numerical computation,the Lyapunov exponent spectrum(Les)of the chaotic attractor are 0.2040,-0.1387. Since the sum of the Lyapunov exponent spectrum of the chaotic attractor is larger than zero, its Lyapunov (Kaplan–Yorke) dimension (Dky)[46]is 2, which demonstrates the chaotic property of the memristive map (2). The correlation dimension of the chaotic attractor of the memristive map(2)is 1.6566 by using the method proposed in Ref. [46]. Finally, whena=0.669,the hidden two-piece chaotic attractors terminate to emerge.

Fig.4. Phase portraits of coexisting solutions of the memristive map(2)with{(x,y)|x ∈[-2.5,2.5],y ∈[-12,12]},(b,c,d,e)=(1.6,1,1,1)and(a)a=0.001(two different cases of hidden period-4 solutions),(b)a=0.015(hidden period-4 solutions),(c)a=0.25(hidden period-8 solutions),(d)a=0.29(hidden multiple-piece chaotic solutions),(e)a=0.304(hidden four-piece chaotic solutions),(f)a=0.331(hidden period-12 solutions),(g)a=0.369(hidden two-piece chaotic solutions),(h)a=0.427(hidden period-10 solutions),(i)a=0.667(hidden two-piece chaotic solutions),respectively.

3.2.2. The case: b=1.7

Figure 5 exhibits random bifurcation and Lyapunov exponent spectrum(Les)diagrams of the memristive map(2)with the parameter(b,c,d,e)=(1.7,1,1,1),whereawas taken as a branch parameter, and the initial states were randomly selected in[-15,15]. In Figs.5(a)and 5(b),the states of the attractors are represented by black dots. In Fig.5(c),the largest Lyapunov exponent (Le1) and the smallest Lyapunov exponent(Le2)are shown by red and blue dots,respectively. Since there are infinitely many coexisting attractors,the range ofyis limited asy ∈[-12,12] in Fig. 5(b). From Fig. 5, we can observe the effect of the parameteraon the hidden multistability of the memristive map (2) and the good accordance between the Lyapunov exponent (Les) diagram and the bifurcation diagram. Figure 6 shows the phase portraits of the coexisting solutions of the memristive map (2) in the range{(x,y)|x ∈[-3,2.5],y ∈[-12,12]}.

From Fig.5,when 0＜a ＜0.034,different cases of hidden solutions coexist. Whena=0.034, the hidden chaotic solutions vanish, and there are only hidden period-16 solutions. Asaincreases to 0.079, there is a period-halving bifurcation, leading the hidden period-16 solutions to hidden period-8 solutions (Fig. 6(a)). Ata= 0.115, the appearance of a period-doubling bifurcation turns the hidden period-8 solutions into hidden period-16 solutions. Then hidden multiple-piece chaotic solutions (Fig. 6(b)) take place after a period-doubling bifurcation cascade. Hereafter, the memristive map (2) exhibits several small windows of hidden periodic solutions (Fig. 6(c)). Then the memristive map (2)goes into chaotic states (Fig. 6(d)) again. After that, we can observe another small window of hidden periodic solutions(Fig. 6(e)), and the memristive map (2) evolves into chaotic states (Fig. 6(f)) again via a period-doubling bifurcation cascade. Finally, whena=0.519, the hidden two-piece chaotic solutions cease to exist.

Fig.5. Random bifurcation diagrams of(a)x,(b)y(y ∈[-12,12]),and(c)Lyapunov exponent spectrum(Les)diagram of the memristive map(2)calculated for a ∈[-0.55,0.55]and(b,c,d,e)=(1.7,1,1,1). The black dots denote the states of the attractors. The red and blue dots represent the largest Lyapunov exponent(Le1)and the smallest Lyapunov exponent(Le2),respectively. The horizontal dashed line refers to the zero value of the Lyapunov exponents.

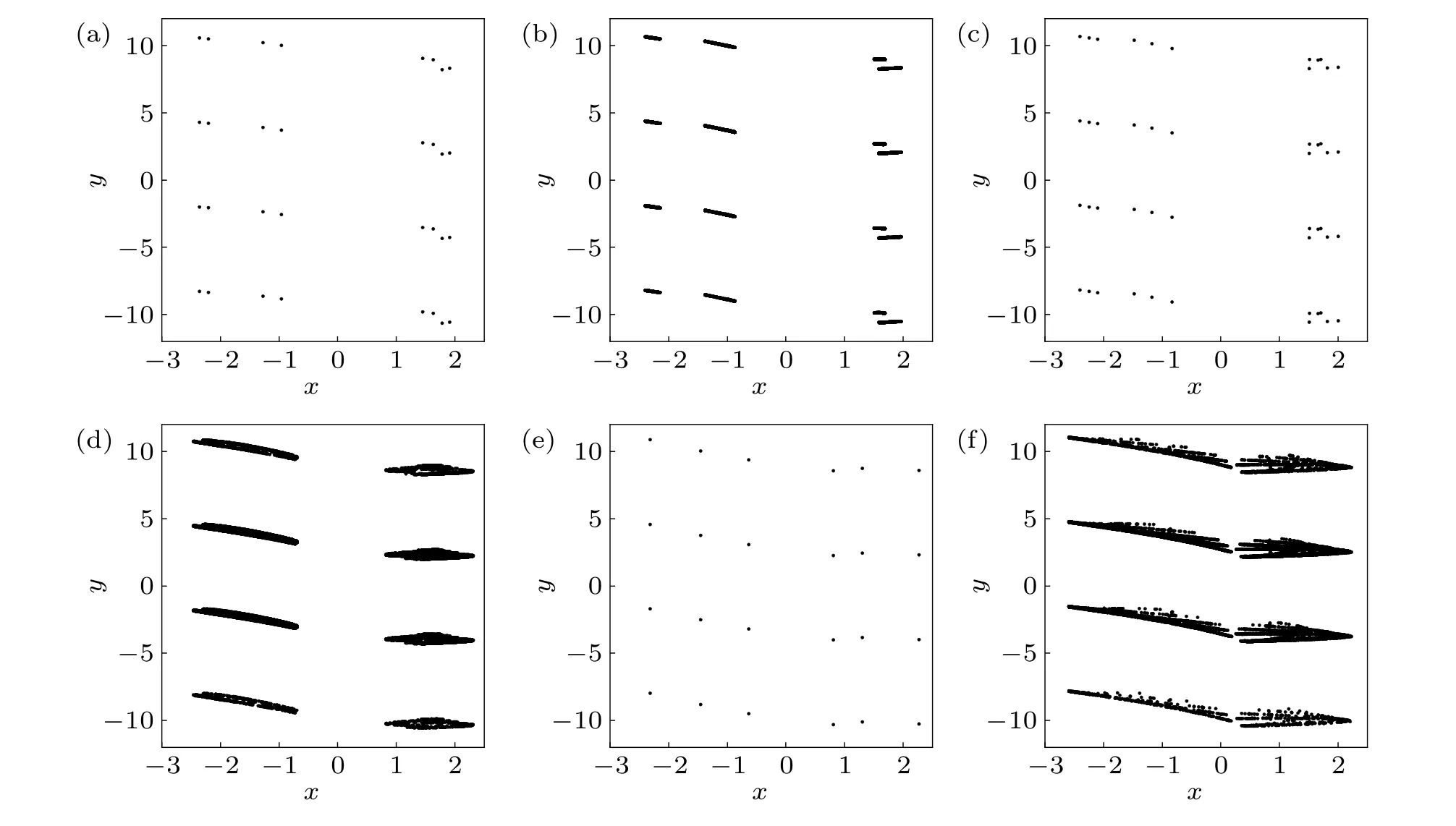
Fig.6. Phase portraits of coexisting solutions of the memristive map(2)with{(x,y)|x ∈[-3,2.5],y ∈[-12,12]},(b,c,d,e)=(1.7,1,1,1)and(a)a=0.079(hidden period-8 solutions),(b)a=0.156(hidden four-piece chaotic solutions),(c)a=0.191(hidden period-12 solutions),(d)a=0.21(hidden two-piece chaotic solutions),(e)a=0.241(hidden period-6 solutions),(f)a=0.518(hidden two-piece chaotic solutions),respectively.

3.3. Bifurcation analysis of parameter b

3.3.1. The case: a=0.1

Figure 7 gives random bifurcation and Lyapunov exponent spectrum diagrams of the memristive map (2) with the parameter(a,c,d,e)=(0.1,1,1,1), wherebwas chosen as a control parameter and the initial states were randomly selected in[-15,15]. In Figs.7(a)and 7(b),the states of the attractors are indicated by black dots. In Fig.7(c),the largest Lyapunov exponent(Le1)and the smallest Lyapunov exponent(Le2)are represented by red and blue dots, respectively. Since there are infinitely many coexisting attractors,the range ofyis chosen asy ∈[-15,15] in Fig. 7(b). From Fig. 7, we can manifest the impact of the parameterbon the hidden dynamics of the memristive map (2) and a perfect accord between the largest Lyapunov exponent (Le1) and the smallest Lyapunov exponent(Le2). Figure 8 illustrates the phase portraits of the coexisting solutions of the memristive map (2) in the range{(x,y)|x ∈[-3,3],y ∈[-12,12]}.

From Fig. 7, whenb= 1.133, the memristive map (2)shows hidden period-2 solutions (Fig. 8(a)). Asaincreases to 1.491, a period-doubling bifurcation occurs, yielding hidden period-4 solutions (Fig. 8(b)). Whenb= 1.681, another period-doubling bifurcation appears, resulting in hidden period-8 solutions (Fig. 8(c)). Atb=1.702, these hidden period-8 solutions turn into hidden period-16 solutions and then evolve into multiple-piece chaos(Figs.8(d)and 8(e))after a period-doubling bifurcation cascade. After that, one can observe a small window of hidden period-6 solutions(Fig. 8(f)) and hidden period-12 solutions. Then the memristive map(2)settles into hidden chaotic solutions(Fig.8(g)).Finally,whenb=1.82,the hidden two-piece chaotic solutions(Fig. 8(h)) are jointed together into hidden one-piece chaotic solutions(Fig.8(i)),which disappear atb=1.942.

Fig.7. Random bifurcation diagrams of(a)x,(b)y(y ∈[-15,15]),and(c)Lyapunov exponent spectrum(Les)diagram of the memristive map(2)calculated for b ∈[-2,2]and(a,c,d,e)=(0.1,1,1,1). The black dots indicate the states of the attractors. The red and blue dots denote the largest Lyapunov exponent(Le1)and the smallest Lyapunov exponent(Le2),respectively. The horizontal dashed line stands for the zero value of the Lyapunov exponents.

Fig.8. Phase portraits of coexisting solutions of the memristive map(2)with{(x,y)|x ∈[-3,3],y ∈[-12,12]}, (a,c,d,e)=(0.1,1,1,1)and(a)b=1.14(hidden period-2 solutions),(b)b=1.5(hidden period-4 solutions),(c)b=1.7(hidden period-8 solutions),(d)b=1.709(hidden five-piece chaotic solutions),(e)b=1.722(hidden two-piece chaotic solutions),(f)b=1.756(hidden period-6 solutions),(g)b=1.766(hidden six-piece chaotic solutions),(h)b=1.8(hidden two-piece chaotic solutions),(i)b=1.835(hidden one-piece chaotic solutions),respectively.

To show the hidden homogenous multi-stability of the memristive map (2), we calculated the basin of attraction of the map whena=0.1,b=1.14,c=1,d=1, ande=1,as demonstrated in Fig.9,respectively. Four hidden period-2 solutions were represented by red, blue, magenta, and black dots,respectively. The basins of these period-2 solutions were colored in orange,yellow,cyan,and green,respectively. From Fig. 9, the basins of attraction of the period-2 attractors are similar.

Fig. 9. Basin of attraction of the memristive map (2) with (a,b,c,d,e)=(0.1,1.14,1,1,1). The unbounded basin of attraction which is the set of initial points going into the region({(x,y)||x|+|y|＞100})is shown in white.The hidden period-2 solutions are denoted by red,blue,magenta,and black dots, respectively. The basins of these period-2 solutions are shown in orange,yellow,cyan,and green,respectively.

3.3.2. The case: a=0.01

Figure 10 displays random bifurcation diagrams and Lyapunov exponent spectrum diagram of the memristive map(2)with the parameter (a,c,d,e) = (0.01,1,1,1), wherebwas treated as a varying parameter and the initial states were randomly taken in[-15,15]. In Figs.10(a)and 10(b), the states of the attractors are denoted by black dots. In Fig. 10(c), the largest Lyapunov exponent (Le1) and the smallest Lyapunov exponent (Le2) are indicated by red and blue dots, respectively. Since there are infinitely many coexisting attractors,the range ofyis selected asy ∈[-15,15]in Fig.10(b). From Fig. 10, we can depict the impact of the parameterbon the hidden multi-stability of the memristive map (2) and a good coherence between the Lyapunov exponent diagram and the bifurcation diagram.

Whenb=1.024, there exists hidden period-4 solutions,which become hidden period-8 solutions through the perioddoubling bifurcation. Whenb=1.028, hidden period-2 solutions arise. So a tiny range of hidden multi-stability is observed. The hidden period-2 solutions continue to exist.However,the hidden period-8 solutions turn to hidden period-16 solutions and finally to chaos via the cascades of perioddoubling bifurcations. The chaotic solutions run away atb=1.01. The hidden period-2 solutions (Fig. 11(a)) bifurcate to hidden period-4 solutions(Fig.11(b))after the perioddoubling bifurcation atb=1.529. Whenb=1.583, another hidden period-4 solutions appear. Then a new range of hidden multi-stability is shown. The two branches of hidden period-4 solutions convert into hidden period-8 solutions, period-16 solutions, and finally into hidden chaotic solutions. So the coexistence of hidden period-8 solution, period-16 solution,and chaotic solutions is observed. In the coexisting region,different types of solutions coexist. Whenb=1.728, there are only hidden two-piece chaotic solutions (Fig. 11(c)). After that, a window of hidden period-6 solutions (Fig. 11(d))and hidden six-piece chaotic solutions (Fig. 11(e)) is found.Whenb=1.812,there are only hidden two-piece chaotic solutions. Whenb=1.847,the two-piece chaotic solutions merge into one-piece chaotic solutions (Fig. 11(f)) which disappear atb=1.928.

Fig. 10. Random bifurcation diagrams of (a) x, (b) y (y ∈[-15,15]), and(b)Lyapunov exponents(Les)diagram of the memristive map(2)calculated for b ∈[-2,-2]and(a,c,d,e)=(0.01,1,1,1). The black dots indicate the states of the attractors. The red and blue dots represent the largest Lyapunov exponent(Le1)and the smallest Lyapunov exponent(Le2),respectively. The horizontal dashed line corresponds to the zero value of the Lyapunov exponents.

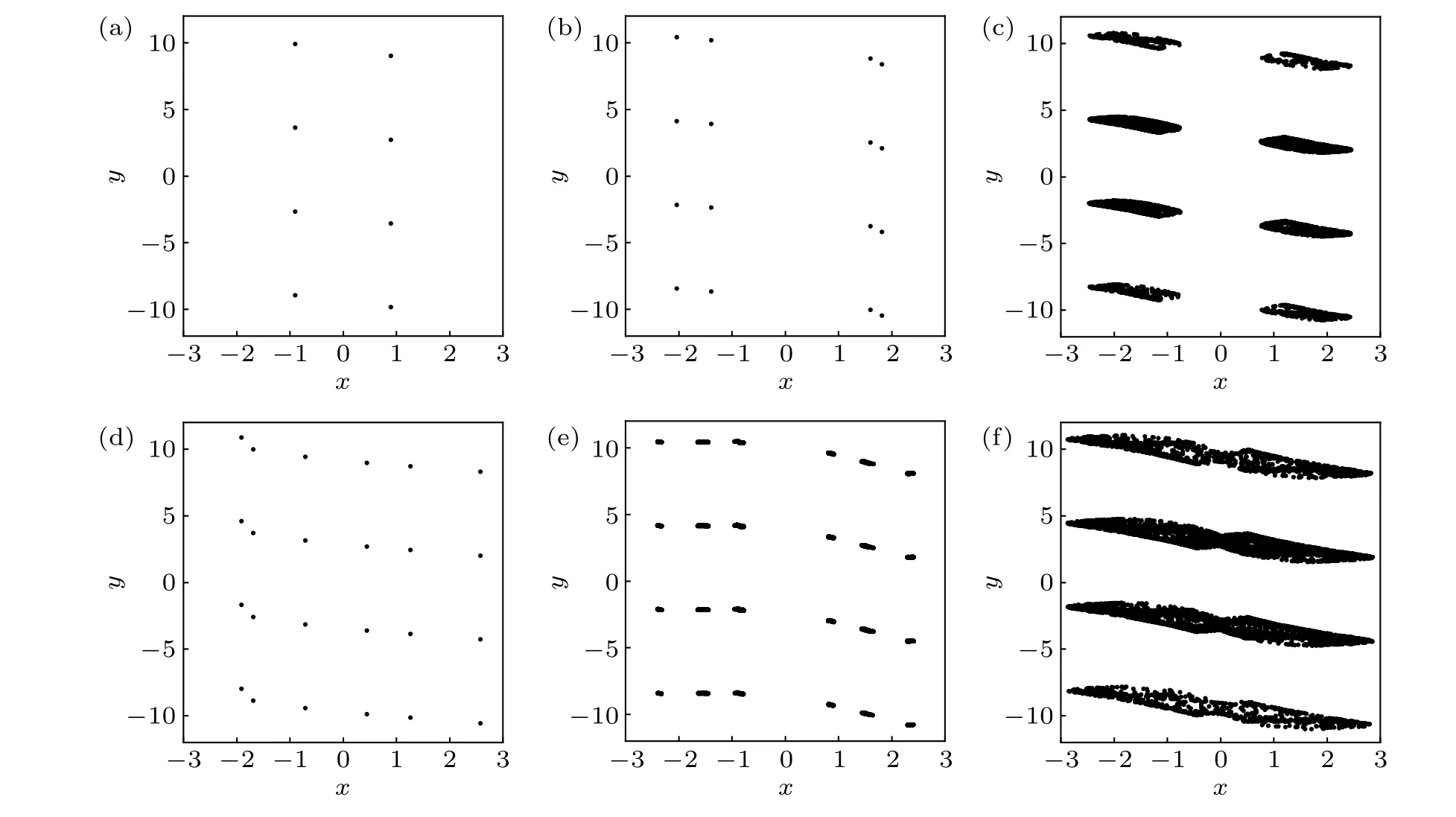
Fig.11. Phase portraits of coexisting solutions of the memristive map(2)with{(x,y)|x ∈[-3,3],y ∈[-12,12]},(a,c,d,e)=(0.01,1,1,1)and(a)b=1.11(hidden period-2 solutions), (b) b=1.58 (hidden period-4 solutions), (c) b=1.728 (hidden two-piece chaotic solutions), (d) b=1.784 (hidden period-6 solutions),(e)b=1.81(hidden six-piece chaotic solutions),(f)b=1.865(hidden one-piece chaotic solutions),respectively.

4. Conclusions

A new class of 2D maps with a cosine memristor was presented and investigated in this paper. We discussed the existence of fixed points of these memristive maps first. Then we employed several numerical analysis tools to demonstrate their complex dynamics, including hidden periodic, chaotic,and hyper-chaotic solutions. The two-parameter bifurcation analysis of the proposed memristive map has been carried out to reveal the bifurcation mechanism of the complex dynamics.The proposed memristive maps can generate infinitely coexisting hidden attractors with the same shape but at different positions. So the map can exhibit the phenomena of extreme homogenous hidden multi-stability. They can potentially be applied to some real applications in secure communication,such as data and image encryptions. Future works will concentrate on investigating the high-dimensional memristive maps with extreme hidden heterogeneous multi-stability.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant Nos.11972173 and 12172340).