基于核估计下概率密度函数的信度模型
2020-04-23温利民吴贤毅
章 溢, 熊 佳, 温利民, 吴贤毅, 周 宪
(1.江西师范大学数学与信息科学学院,江西南昌330022;2.江西财经大学统计学院,江西南昌330013;3.华东师范大学统计学院,上海200062;4.麦考瑞大学统计与精算学系,澳大利亚悉尼2109)
§1 引 言
在非寿险精算中,常用非负随机变量X表示风险的损失.一般地,风险X的分布依赖某个风险参数θ,记f(x;θ)表示风险X的密度函数或概率分布律.由于保单风险的非齐次性,所有θ的取值形成某个概率分布π(θ).在Bayes统计中,π(θ)被称为先验分布,在精算学中又被称为结构函数.假设对风险X已经有若干年的索赔记录X1,···,Xn,可看成θ给定条件下的独立同分布的随机样本.本文的目的是通过结合样本信息和先验分布信息对风险X或其分布f(x;θ)进行估计或统计推断.显然,对f(x;θ)的统计推断落入了Bayes框架.
在非寿险精算中,信度理论是解决非齐次保单定价的一种重要方法,在保费厘定,责任准备金评估等方面都有广泛的运用[1-6].假设随机变量X1,···,Xn与X是在风险参数θ给定条件下相互独立同分布的随机变量,其共同的密度函数为f(x;θ).为了预测未来的损失X或估计条件均值µ(θ)=E(X|θ),Bühlmann[1]建议将估计限定在样本的线性损失函数下,求解下面的最小化期望平方损失问题
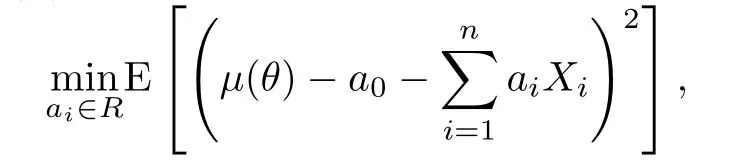
得到了条件均值µ(θ)的信度估计表达为下面的加权平均形式:

其中µ0=E[µ(θ)]为保单组合的聚合保费,而权重

被称为信度因子.这里φ=E[Var(X|θ)],ρ=Var(µ(θ))
在数理统计中,核密度估计是密度函数的一种最为流行的非参数估计方法.核估计方法首次由Rosenblatt[11]提出,在生物统计,医学统计,教育统计等领域有广泛的运用[12-15].
借助核估计思想,本文将建立损失额分布的Bayes模型,将条件密度的估计限定在核函数的线性结构中,通过求解最小化期望积分损失函数,得到密度函数的信度估计.进而通过代入的方法得到具有安全负荷的保费原理中风险保费的信度估计.后面的内容安排如下.§2介绍核密度估计并建立损失密度函数的Bayes模型.§3讨论密度函数的核估计及其统计性质.§4在一些保费原理中,获得风险保费的信度估计,并与已有的信度估计进行比较.
§2 模型的准备与设定
记F(x)=P(X≤x)为风险X的分布函数,相应的密度函数为f(x).假设X1,···,Xn为该总体的n个独立同分布样本.对给定的x>0,定义经验分布函数为

容易得到经验分布函数的期望和方差为
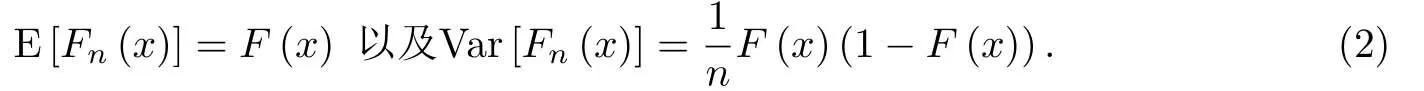
因此Fn(x)是F(x)的无偏相合估计.
注意到密度函数是分布函数的导数,根据导数的定义有

容易想到f(x)的一个近似估计为
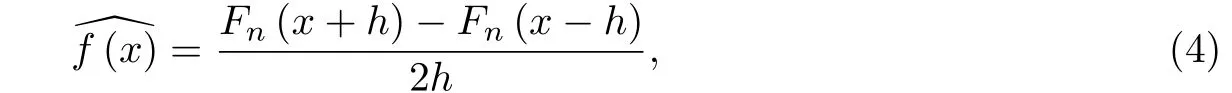
其中h是一个给定的小的正数.如果令

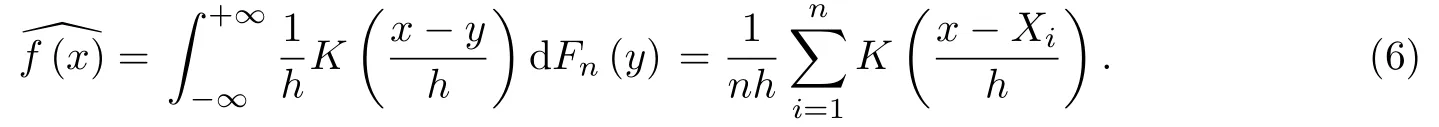
其中K(y)被称为核函数.进一步地,令Kh(·)=K(·/h)/h.记
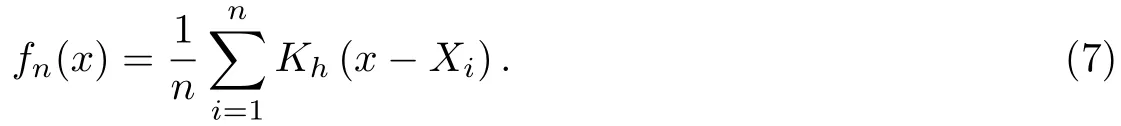
当K(y)不取为(5)式而取更一般的核函数时,估计(7)被称为核密度估计或核估计.其中h被称为窗宽.
首先容易证明核密度估计fn(x)是渐近无偏估计[11],即有

一般地,窗宽h的选取与样本容量n有关,且有对于核函数K(y),常常选取偶函数且满足:.常用的核函数有均匀核,高斯核,三角核以及Epanechikov核等.
在信度理论中,保单的损失额度X常常是连续型随机变量,具有某个概率密度函数f(x;θ),其中θ一般表示该风险的特征.例如,在汽车第三者责任保险中,θ为汽车的型号,行驶里程数,司机的年龄,性别,工作性质等与风险相关的综合因素总和.由于保单的非齐次性,θ一般为随机变量,具有某个先验分布π(θ).
在保险合同中,被保险人通过缴纳一定的保费将风险X转嫁给保险公司.显然,保费的多少是该保单合同成立的关键.精算师通过分析X的分布,通过某种方法确定风险X保费.这种确定保费的方法称之为保费原理.
定义1.1设X为非负随机变量,具有密度函数f(x;θ).保费原理即为对风险X分配一个固定的数额H(X),记为X 7−→H(X)或f(x;θ)7−→H(f(x;θ)).
在实际中,常用的保费原理有期望值原理,方差原理,标准差原理,Esscher保费原理,指数保费原理等等.关于保费原理的详细介绍可参考[16].经典的信度理论仅给出了净保费原理的经验厘定方法.近年来,已有许多文献讨论各种保费原理下风险保费的经验厘定问题.大部分研究都是通过将平方损失函数修改为其他损失函数的方法,获得某些特殊的保费原理中风险保费的信度估计及其经验厘定[7,9-10].然而,对于某些保费原理,例如方差保费原理,标准差保费原理,分位数保费原理,它们不能通过修改损失函数的方法得到.注意到,不管是什么保费原理,总能表达为密度函数的某个泛函H(f(x;θ)).如果能获得密度函数的信度估计,则通过代入的方法即可获得该保费原理中风险保费的信度估计,即为

因此,下一节将探讨密度函数的信度估计问题.
§3 基于核函数下密度函数的信度估计
考虑一个保单合同,被保险人面临的可能损失为X.在风险参数θ给定条件下,风险X的密度函数为f(x;θ).由于风险的非齐次性,假设风险参数θ为随机变量,服从某个先验分布π(θ).设(X1,···,Xn)分别为该风险在n个保单期的索赔样本.本文的目的是根据样本信息和先验信息估计条件密度函数f(x;θ),进而估计风险X的保费H(f(x;θ)).
根据Bayes定理,对给定的x>0,条件密度函数f(x;θ)的后验均值
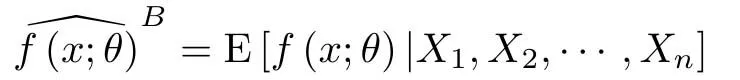
是平方损失函数下f(x;θ)的最优估计,即有





§4 基于密度函数的信度估计的保费厘定





表1 当样本容量n=10的均方误差及估计效率

表2 当样本容量n=50的均方误差及估计效率
模拟结果表明,在窗宽较小的情况下,即使小样本容量也能保证估计有较小的均方误差,随着样本容量增大,估计的效率很快收敛到1.
