具有动态边界的记忆阻尼Timoshenko梁的稳定性
2020-04-23鲁轶戈章春国
鲁轶戈,章春国
(杭州电子科技大学数学系,浙江杭州310018)
§1 引 言
近二,三十年来,现代控制理论在空间飞行器控制中处于迅猛发展阶段,在带有大量燃料及挠性部件的大型应用卫星控制中,为了解决振型及频率不准确的控制以及部件闭路系统中优化控制的难题,人们正在积极开展控制理论应用的探索研究.于此同时,由于柔性结构在空间科学及机器人学中被广泛应用,空间柔性结构的控制问题也引起了人们广泛的关注,而Euler-Bernoulli梁,Timoshenko梁以及Rayleigh梁扮演了重要的角色,其中尤以Timoshenko梁能更精确地描述一类弹性梁模型,因此能更好地满足实际应用的需求(参见文献[1-3]).
许多数学与力学工作者都致力于研究具有粘弹性阻尼的弹性梁系统的稳定性.如:Liu和Liu在[4-5]中研究了抽象粘弹性系统与具有局部粘弹性的振动弦的指数稳定性;赵宏亮在[6]中研究了具局部粘弹性(Kelvin-Voigt阻尼和Boltzmann阻尼)的弹性系统的稳定性;章春国在[7]中对只具有一个局部记忆阻尼的非均质Timoshenko梁的稳定性进行了研究,借助波速点点相等的条件得到了该系统的指数稳定性;在文献[8]中,Ma等研究了Timoshenko梁方程与热方程耦合系统的指数稳定性;Rivera等在[9]中研究的是具有全局记忆阻尼的Timoshenko梁系统的一致指数稳定性;Rivera等在[10]中研究了一类Timoshenko梁系统的Signorini问题,引入混合惩罚法给出了局部耗散模型的多项式衰减估计.
本文主要研究的是具有动态边界的局部粘性阻尼的Timoshenko梁的稳定性,更确切地说,考虑如下初边值问题:
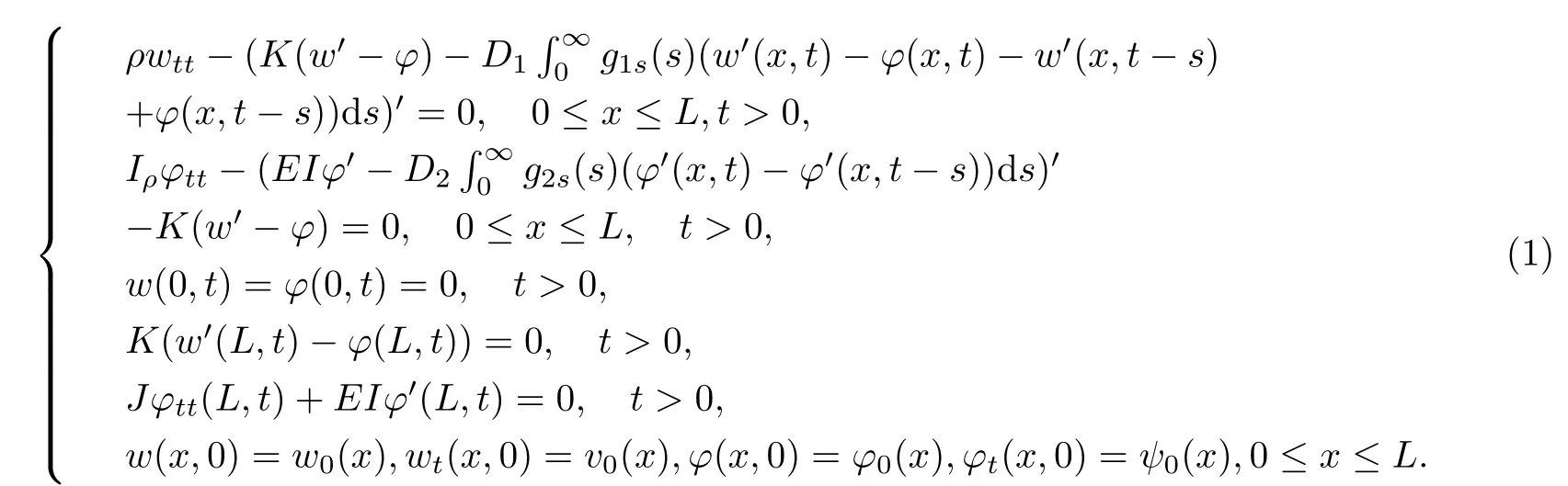
§2 主要结果
为了研究系统的能量衰减估计,需要下面的自然假设.


§3 系统的适定性和半群的谱性质


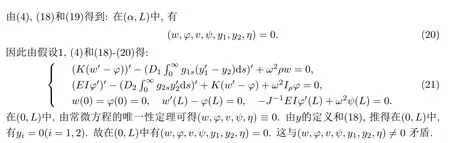
§4 定理2.2的证明





