雅鲁藏布江下游墨脱江段黄斑褶鮡的年龄结构与生长特征

金洪宇，李 雷，金 星，王念民，马清芝，尹家胜，马 波

(1.水产科学国家级实验教学示范中心(上海海洋大学)，上海 201306；2.水产种质资源发掘与利用教育部重点实验室(上海海洋大学)，上海 201306；3.农业部淡水水产种质资源重点实验室(上海海洋大学)，上海 201306；4.中国水产科学研究院黑龙江水产研究所，哈尔滨 150070)

西藏地区独特的高原生态环境孕育着特殊鱼类物种，鱼类区系主要由裂腹鱼类(Schizothorax)、高原鳅类(Plateauloach)和鰋鮡鱼类(Glyptosternoidfishes)组成[1]，其中鮡科鱼类具有生命周期长、生长速度缓慢等生物学特性[2]。由于雅鲁藏布江位处高原，海拔高、水温低，鱼类生长速度与较低海拔地区相比较为缓慢[3]。

鱼类的年龄结构与生长特性是研究鱼类生物学的重要内容，也为渔业自然资源的保护管理提供基础资料[2]。有关文献表明在鮡科鱼类的年龄鉴定过程中，已使用耳石[3]、脊椎骨[4]、胸鳍棘[5]等作为年龄鉴定材料。近年来，对分布于青藏高原的扁头鮡(PareuchiloglaniskamengensisJayaram)[3]、黑斑原鮡(Glyptosternummaculatum)[4]等高原鮡科鱼类的年龄结构与生长特性进行研究，为高原鱼类的保护研究提供了基础数据。

黄斑褶鮡(Pseudecheneissulcatus)，隶属鲇形目(Siluriformes)鮡科(Sisoridae)褶鮡属(Pseudecheneis)，俗称褶赖、绒布，为底栖性中小型鱼类，栖息在山涧溪河多砾石的急滩，常吸附于石块上生活[6]。黄斑褶鮡为西藏土著特有鱼类，在中国仅分布于雅鲁藏布江中、下游[1]，其中以墨脱附近干支流为主要分布区，分布海拔最高可达2 960 m[7]。目前对于黄斑褶鮡的研究仅限于形态[8]、体长体重关系[9]、系统发育[10]等方面的工作，然而黄斑褶鮡年龄与生长方面的研究尚未见报道。本文首次对雅鲁藏布江下游墨脱江段黄斑褶鮡的年龄结构与生长特征进行了系统研究，以探求其生长规律，旨在为资源的保护管理提供科学依据。

1 材料和方法

1.1 样品采集

2018年3月和7月，于西藏雅鲁藏布江下游墨脱江段(29°18′N，95°16′E)采集黄斑褶鮡样本，采样地点位于西藏墨脱县境内，海拔约600 m，两岸为高山峡谷，河道底质为直径大于256.0 mm的巨岩，河岸带植被主要为林地(图1)。主要使用定置刺网(网眼大小1～3 cm)及小型电捕器(输出功率600 W)对黄斑褶鮡进行采集，共采集203尾。全部样本在新鲜状态下测量体长(精确至0.1 mm)，电子天平称重(精确至0.1 g)。解剖样本取出生殖腺，判断性别。取出左、右微耳石，放入盛有无水乙醇的培养皿中，进行清洗，去除耳石表面粘膜，风干后，分别放入2 mL离心管中，带回实验室进行处理。取第2～5节脊椎骨，剔除表面肌肉及结缔组织，放入50 mL离心管中，带回实验室进行处理。

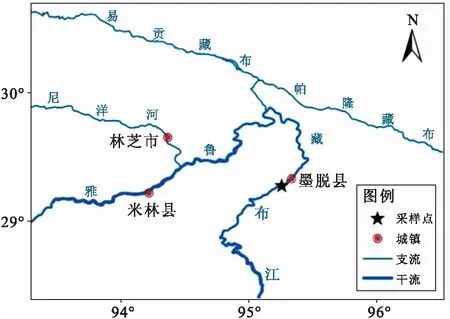
图1 黄斑褶鮡采样地点位置图Fig.1 Geographical location of sampling sites for P.sulcatus

1.2 材料处理

以脊椎骨和微耳石做为鉴别年龄的材料，每尾样本取第2～5节脊椎骨，煮沸5 min，在自来水下进行冲洗，用镊子剔除附着表面的肌肉及结缔组织，自然干燥12 h，放入5%的双氧水中浸泡24 h，将椎体放入盛有二甲苯的培养皿中，使用解剖镜在通风橱下进行观察。将微耳石用无色透明指甲油固定于载玻片上，先使用500#砂纸进行打磨，再使用2000#砂纸精细打磨，打磨过程中在显微镜下观察，待打磨至中心时，将微耳石翻至另一面，继续上述操作，打磨到轮纹清晰可见为止。在显微镜下用反射光进行观察，可以发现以生长中心核为圆心，呈同心圆状排列的透明带和暗带，一个透明带和一个暗带构成一个年轮。将脊椎骨和耳石尚无年轮形成，划分为0龄组，将已形成第1个年轮和轮纹外已有第2年的生长环片，但未形成第2个完整轮纹的个体，划分为1龄组，将已形成第2个年轮和轮纹外已有第3年的生长环片，但未形成第3个完整轮纹的个体，划分为2龄组，以此类推，对年龄组进行划分。

1.3 数据处理

体长体重关系采用W=aLb公式进行拟合，其中W为体重(g)，L为实测体长(mm)，a、b分别为通过回归分析估算的常数和指数；以体长作为协变量进行协方差分析，检验雌、雄个体之间体长体重关系是否存在差异。依据t检验，分析指数b与3之间是否存在显著性差异，当t值小于t(0.05，(n-2))值时，表示差异不显著，为匀速生长，否则差异显著，为异速生长。

根据体长、体重数据采用VBGF、Compertz GF、Logistic GF[11]三种生长方程，进行生长分析，公式如下：

VBGF:Lt=L∞[1-e-k(t-t0)]+ε

Compertz GF:Lt=L∞e-e(-k(t-t0))+ε

LogisticGF:Lt=L∞/(1+e-k(t-t0))+ε

式中L∞表示渐进体长，k表示趋近渐近值的相对速度，t0表示理论上的起点年龄，ε表示加性误差(符合正态分布)。采用AIC准则(赤池信息量准则)和BIC准则(贝叶斯信息准则)和R2(拟合优度)[12-13]进行筛选，AIC和BIC值最小者为最适生长方程。

所有数据的分析采用SPSS20.0和Microsoft Excel 2016软件处理，所有图片使用Photoshop6.0进行图像处理。

2 结果与分析

2.1 不同鉴定材料的年轮特征

黄斑褶鮡的微耳石呈不规则圆形，薄且透明，直接观察无明显轮纹。打磨加工后，可见轮纹，但较为模糊，且成功率低，打磨35份，年轮清晰可见的仅有5份，即微耳石不适合作为黄斑褶鮡的年龄鉴定材料。黄斑褶鮡的脊椎骨经处理，显微镜下观察，可发现脊椎骨略呈椭圆形，在解剖镜的投射光下可见l宽带与1窄带相间隔，组成l个年带层，且宽带比窄带颜色较浅。由于窄带宽度小而均匀，作为年带层的分界线更为合适，故称为年轮(图2)。脊椎骨年轮间距逐渐缩小，越接近脊椎骨边缘间距越小，但观察部分脊椎骨时其间距会突然的跳跃。因此本研究选用脊椎骨作为黄斑褶鮡年龄鉴定材料，通过对比有183份脊椎骨可进行年龄判断。

图2 雅鲁藏布江黄斑褶鮡的脊椎骨Fig.2 Spine of P.sulcatus in Yarlung Zangbo River短线表示年轮；SR：脊椎骨半径

2.2 体长、体重及年龄组成

样本体长范围为50.0～144.0 mm，平均体长为(99.1±18.7)mm，优势体长为70.0～110.0 mm，约占73.22%(图3)；样本的体重范围为3.8～65.6 g，平均值为(26.0±14.7)g，优势体重为10～30 g，约占62.84%(图4)。群体年龄由1～9龄组成，其中优势年龄为2～5龄，占全部样本数的73.22%。

性别可辨认的样本为180尾，雌性90尾，雄性90尾，性比为1∶1，另有3尾无法判断性别。雌性样本体长范围为50.0～140.0 mm，平均体长为(94.0±18.4)mm。体重范围为3.8～64.1 g，平均体重为(22.3±13.9)g。雄性样本体长范围为69.3～144.0 mm，平均体长为(104.1±17.7)mm。体重范围为8.4～65.6 g，平均体重为(29.6±14.7)g(表1)。

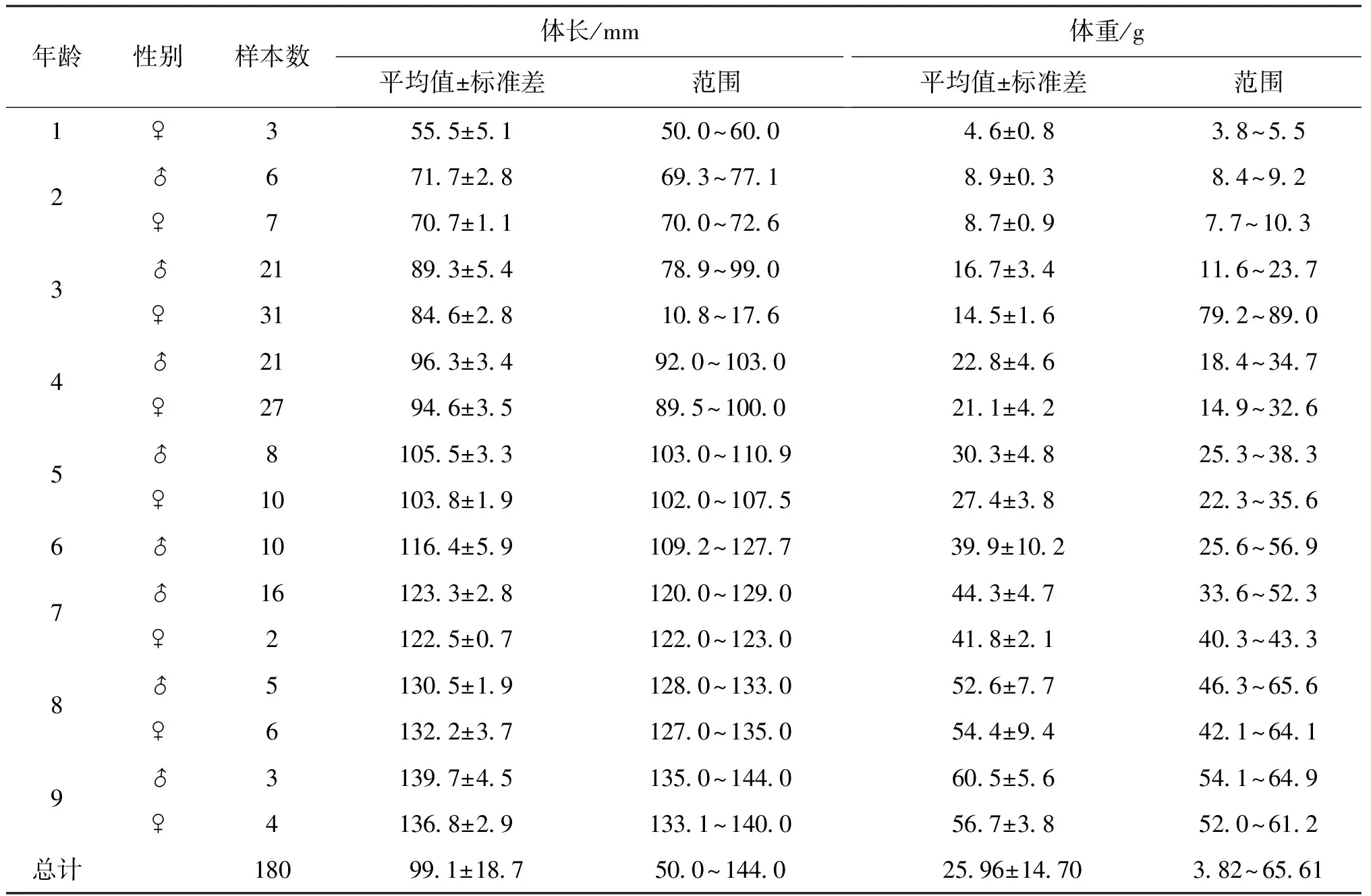
表1 黄斑褶鮡各年龄组的生长参数Tab.1 Growth indices in P.sulcatus in different age classes

图3 黄斑褶鮡体长频数分布Fig.3 The body length distributionn of P.sulcatus

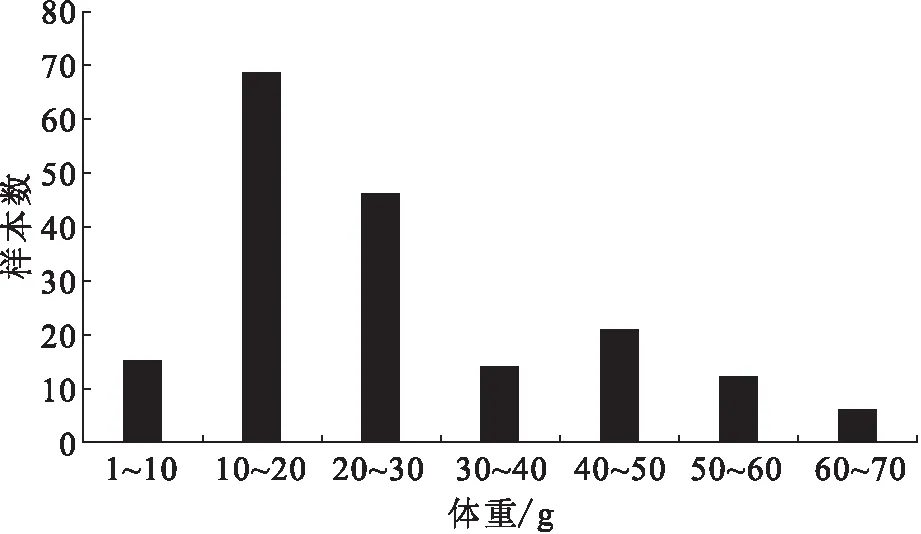
图4 黄斑褶鮡体重频数分布Fig.4 The body weight distributionn of P.sulcatus

2.3 生长特性

2.3.1 体长与体重的关系

采用W=aLb公式对雌、雄样本实测体长(L)和体重(W)分别进行拟合，得到关系式：W♀=4×10-5L2.8875(R2=0.97,n=90),W♂=3×10-5L2.9961(R2=0.95,n=90)。

以实测体长为协变量，进行协方差分析(ANCOVA)，结果显示雌、雄群体体重之间无差异(F=0.134,P=0.715>0.05)。因此将雌、雄样本进行统一分析，得到关系式：W=3×10-5L2.9292(R2=0.96，n=183)(图5)。对全部体长体重关系式的幂函数进行t检验结果表明体长体重关系幂指数与3差异不显著(t=0.605

图5 黄斑褶鮡的体长与体重关系Fig.5 Relationship between body length and body weight of P.sulcatus

2.3.2 生长退算

共测量样本183尾，其中雌性样本90尾，雄性样本90尾，未辩明性别3尾。以实测体长为协变量，进行协方差分析(ANCOVA)，结果显示雌、雄群体脊椎骨半径之间无差异(F=0.761，P=0.384>0.05)。对脊椎骨横突方向的半径(R)与体长(L)进行拟合(图6)，得到直线函数相关：L=62.88R+40.69(R2=0.89,n=183)；幂函数相关：L=104.67R0.6236(R2=0.89,n=183)。两者均能较好的拟合脊椎骨半径与体长的关系，但脊椎骨半径接近于0时，直线相关式退算体长较幂函数关系式退算体长相比较大，因此选择直线相关式进行生长退算。将脊椎骨各年轮的轮径代入体长与脊椎骨半径关系式进行退算得到各年龄组的推算体长(表2)。

表2 黄斑褶鮡的实测体长和推算体长Tab.2 Measured and back-calculated total length of P.sulcatus

图6 黄斑褶鮡的脊椎骨半径与体长关系Fig.6 Relationship between body length and spine radius of P.sulcatus

2.3.3 生长方程

根据实测数据，选用Compertz GF、Logistic GF、VBGF分别拟合了黄斑褶鮡的体长生长方程。从生长方程的拟合结果可以看(表3)，三种生长方程的拟合均具有较高的拟合度(R2>0.99)，其中Compertz GF和Logistic GF的R2为0.97，均低于VBGF的相关系数，且VBGF的AIC值和BIC值最低。因此，选用VBGF对黄斑褶鮡进行生长描述时，可以更好的描述黄斑褶鮡生长特性。

运用非线性回归法将黄斑褶鮡各年龄组实测体长的平均值与von Bertalanffy生长方程进行拟合，求得各参数值：L∞=189.56 mm；k=0.118；t0=-1.981；W∞=155.45 g。由此得出黄斑褶鮡的体长、体重生长方程如下：

表3 黄斑褶鮡的生长模型检验Tab.3 Values for the fitness of P.sulcatus body length with different growth equations

Lt=189.56[1-e-0.118[t+1.981]]

Wt=155.45 [1-e-0.118[t+1.981]]2.9292

根据体长、体重生长方程绘制黄斑褶鮡的生长曲线(图7)。

图7 黄斑褶鮡体长体重生长曲线Fig.7 The growth curves of standard length and body weight in von Bertalanffy functions of P.sulcatus

2.3.4 生长速度与生长加速度

对黄斑褶鮡的体长、体重的生长方程分别求一阶导数和二阶导数，得到体长、体重的生长速度及生长加速度方程：

dL/dt=22.37e-0.118(t+1.981)

dW/dt=53.57e-0.118(t+1.981)(1-e-0.118(t+1.981))1.9292

d2L/dt2=-2.639e-0.118(t+1.981)

d2W/dt2=6.34e-0.118(t+1.981)(1-e-0.118(t+1.981))0.9292(2.9292e-0.118(t+1.981)-1)

分别绘制上述方程的曲线(图8，9)。黄斑褶鮡体长生长速度和体长生长加速度不具备拐点，体长生长速度随着年龄的生长而逐渐下降，均为正值，说明体长生长速度在0龄时最大，随着年龄增长递减速度缓慢，体长趋近渐近值。随着年龄增长，体长生长加速度逐渐上升，逐渐趋近于0(图8)。黄斑褶鮡体重生长速度先上升后下降，具有生长拐点，此时体重生长加速度为零(d2W/dt2=0)，体重生长速度达到最大值(图9)。将生长方程参数b、k、t0代入方程tIP=lnb/k+t0，求得黄斑褶鮡生长拐点为7.1龄，对应的体长、体重为Lt=124.6 mm，Wt=45.5 g。

3 讨论

3.1 年龄鉴定材料的选择

年龄鉴定是鱼类生物学研究的重要内容，也为构建鱼类资源评估模型提供基础依据[14]。鱼类年龄鉴定过程中，常用材料主要包括鳞片、耳石、鳍条、脊椎骨和鳃盖骨等[2]，并不是所有鱼类的年龄鉴定材料都能进行有效判读，需要比较不同鉴定材料的判读效果、可操作性，选择最适材料进行年龄鉴定[15]。有关研究表明脊椎骨是大多数鲇形目鱼类的最佳年龄鉴定材料[4、16-21]。李秀启等[17]以脊椎骨作为黄颡鱼(Pelteobagrusfulvidraco)的年龄鉴定材料。李红敬[4]以脊椎骨、耳石、胸鳍棘作为材料，对黑斑原鮡年龄进行鉴定，脊椎骨鉴定效果最为理想。申严杰等[18]以脊椎骨和胸鳍棘作为材料对福建纹胸鮡(Glyptothoraxfukiensis)年龄进行鉴定，结果表明脊椎骨鉴定效果最佳。杨德国等[19]研究发现，长吻鮠(Leiocassislongirostris)可使用脊椎骨和胸鳍棘进行年龄鉴定，鉴定结果相近，均可准确鉴定年龄，该结果与黄静等[5]对大鳍异鮡(Creteuchiloglanismacropterus)年龄鉴定材料选择结果相同。王志玲等[20]以脊椎骨作为主要鉴定材料，耳石或胸鳍棘作为对照材料，对大口鲇(SilurusmeriordinalisChen)进行年龄鉴定，这与段中华等[21]对瓦氏黄颡鱼(P.vachelli)和王永明等[22]对黄石爬鮡(Euchiloglaniskishinouyei)进行年龄鉴定时，所用的年龄鉴定材料相同。因此脊椎骨在鮡科鱼类年龄鉴定中，可作为可靠材料。黄斑褶鮡为小型无鳞鱼类，其微耳石薄而小，打磨后较为模糊，不易读取年轮，鉴定成功率低。胸鳍棘需包埋切片进行观察，材料处理复杂。脊椎骨操作简单，可批量操作，年轮结构清晰，易于观察。因此，脊椎骨为黄斑褶鮡的最佳鉴定材料。

图8 黄斑褶鮡体长生长速度及生长加速度曲线Fig.8 Curves of growth rate and its acceleration of body length in von Bertalanffy functions of P.sulcatus

图9 黄斑褶鮡体重生长速度及生长加速度曲线Fig.9 Growth rate curve and acceleration of body weight in von Bertalanffy functions of P.sulcatus

3.2 黄斑褶鮡生长方程的选择

鱼类生长是同化作用与异化作用两个相反过程机制共同作用的结果[2]。生长方程是用以表达鱼类生长特点的函数式，随着鱼类年龄的生长其参数值不发生改变[23]。描述鱼类生长特性的生长方程种类繁多、各有特点，不同生长方程在描述鱼类生长特性时的侧重点各不相同，因此需要选择最为适合的生长方程对鱼类生长进行准确描述[24]。段中华等[21]使用VB GF、Logistic GF和Gompertz GF对瓦氏黄颡鱼的生长进行了模拟，结果表明，Gompertz GF为瓦氏黄颡鱼的最适生长方程。尹邦一等[26]使用VBGF、Logistic GF和Gompertz GF对长脂拟鲿(Pseudobagrusadiposalis)的生长进行模拟，其中VB GF的描述效果最佳，Gompertz GF次之，Logistic GF效果最差。本文为了准确概述黄斑褶鮡的生长特性，使用VB GF、Compertz GF、Logistic GF三种生长方程分别对黄斑褶鮡的体长生长进行拟合，通过对比R2、AIC、BIC的数值，选择最佳拟合方程。结果表明VB GF为最适生长方程，Logistic GF拟合效果最差。据殷名称报道鱼类体长体重关系式中参数b值接近3，VBGF的拟合效果最佳[2]，本研究中黄斑褶鮡的b值为2.9292，经t检验结果表明体长体重关系幂指数与3差异不显著。Logistic GF受到鱼类生境的环境容纳量影响，自然环境下受食物和栖息地影响[26]。Compertz GF适用于生命周期较短的r选择生物模型，黄斑褶鮡生命周期较长[4、24]，不适用于该方程。生长方程受到种类、环境、生长阶段等因素的影响，通过生长方程的参数检验，选择最适模型描述鱼类生长概况。

3.3 黄斑褶鮡的生长特性

在体长体重关系方程W=aLb中，b值与3不存在显著差异，即黄斑褶鮡为匀速生长。本研究中，黄斑褶鮡雌、雄个体生长无显著性差异，这与大鳍异鮡[5]、大鳍鳠(Mystusmacropterus)[27]、瓦氏黄颡鱼(P.vachelli)[21]结果一致。研究表明，k值范围为0.05～0.10的鱼类为缓慢生长鱼类，0.10～0.20为中速生长鱼类，0.20～0.50为快速生长鱼类[28]。黄斑褶鮡k值为0.118，属于中速生长的鱼类。与其它鮡科鱼类对比发现，黄斑褶鮡的k值相对较大。高原鮡科鱼类扁头鮡[3](♂0.073)、黄石爬鮡[22](0.089)、大鳍异鮡[5](0.049)和黑斑原鮡[4](♂0.088)k值较小，属于缓慢生长鱼类。与扁头鮡[3](♀0.107)、黑斑原鮡[4](♀0.114)的k值接近，而低海拔的福建纹胸鮡[18](0.254)的k值较高，属于快速生长鱼类，远高于黄斑褶鮡。黄斑褶鮡k值与其他鮡科鱼类存在差异，究其原因，可能是因为存在种间差异，同时也受水体饵料丰富度、水温等环境因素的影响。由于黄斑褶鮡采样地点环境恶劣，采样困难度较大，并未进行全年样品采集，可能对黄斑褶鮡生长特性的研究造成影响。

3.4 资源保护

黄斑褶鮡为小型中速生长鱼类，种群规模较小，生境地理位置偏僻，处于原始自然状态，容易遭到破坏，加之近年来西藏水电站的建设对河道环境的改变，使其资源大量消减，需尽快制定相关的保护策略，落实相关禁渔政策，加强对黄斑褶鮡资源的保护。生长方程估算雅鲁藏布江下游黄斑褶鮡生长拐点年龄为7.1龄，对应的体长、体重为Lt=124.6 mm，Wt=45.5 g，为黄斑褶鮡的自然资源保护提供了理论依据。建议将黄斑褶鮡列为重点保护鱼类物种，并为其建立自然保护区，对其栖息地环境进行全面保护，避免遭到破环，同时，建议相关部门应加强相关的科学研究，开展人工繁育工作，可进行野外增殖放流工作，增加种群数量，保证种群的维持和可持续发展。