第三届国际数学教材研究与发展会议综述
2020-04-22綦春霞
綦春霞,曹 辰,付 钰
第三届国际数学教材研究与发展会议综述
綦春霞,曹 辰,付 钰
(北京师范大学,北京 100875)
2019年第三届国际数学教材研究与发展会议主要包括教材的研究理论、教材的开发、教材内容的呈现方式、教材的发展、教材的比较、数字教材等主题.通过对会议论文及会议发言的梳理,可以归纳出国际数学教材研究的最新观点、成果与方向,并为中国数学教材研究提供一定的借鉴.
教材内容呈现;教材比较;教材历史;数字教材
继第一届在英国、第二届在巴西,第三届国际数学教材研究与发展会议于2019年9月16—19日在德国帕德博恩召开,来自美国、英国、德国、中国、日本、韩国、新加坡、巴西、法国、南非、以色列、瑞典等18个国家的一百九十多位专家出席了会议.按照大会议程,第四届国际数学教材大会将于2021年在北京师范大学召开.为了更好地借鉴国际经验,提升中国数学教材研究的水平,这里试图对第三次国际数学教材会议的内容进行介绍,以期对中国的数学教材研究提供一定的借鉴.
此次会议共包括4场大会报告、4场专题讨论会以及两场工作坊和多场小组会议研讨,主要涉及数学教材的分析与评价、数学教材的内容分析、数学教材的比较、数学教材的使用、数学教材的开发、信息技术和电子平台6个方面.
1 基于理论的数学教材分析与评价
关于教材分析与评价的研究是此次会议的重要议题,德国莱布尼茨科学和数学教育研究所的Henning Sievert等学者发现,教材质量对于学生的学业成绩有显著影响.此次会议着重关注从理论角度去分析和评价教材,是数学教材研究的最新方向.
1.1 教学认识论
在此次会议中,多国学者利用人类行为学中的“ATD(anthropological theory of didactics)”模型[1],展示了他们在教材评价上的成果.日本鸣门教育大学的Toru Hayata与Sakura Amor学者对日本一~六年级几何教材中所提出的问题进行了分析,以研究这些问题是否可以支持学生几何思维的发展.其结果发现,一~五年级教材中设置的问题可以支持学生几何思维的发展,而六年级教材中则存在一定问题,因为其关于图形性质、变换、数学活动的问题数量明显减少.据此提出建议,在六年级教学中,教师需要对教学方法进行适当调整,或者教材需要重新设计.挪威科技大学的Solomon A. Tesfamicael等学者对于挪威教材中多种函数概念表征间的转换方式进行了分析.结果发现,大部分表征方式之间的转换过程符合ATD理论,可以有效帮助学生加深对函数概念的理解,但也存在一些转换过程不符合ATD理论.基于以上发现,他们建议可以基于ATD理论,对教材内容进行标定并修正,以提高教材的使用效果.而德国帕德博恩大学的Tobias Mai与Rolf Biehler应用以上理论,对3本德国教材中向量概念的引入方式进行了比较研究.研究表明,每本教材对向量的引入方式均有所不同,有些侧重于从代数角度进行引入,有些则从几何的角度.而德国锡根大学的Frederik Dilling对以上问题进了进一步探索,他发现几何方法在数学和物理教材中占主导地位.进而提出,为了让学生全面理解向量概念,应将概念的不同方面都呈现给学生,向量在数学和物理课中的应用应协调一致,这样学生就不会在单一学科中形成片面的向量概念.具体地,物理课应强调矢量的代数表示,数学课应强调矢量的物理应用.教师不仅要学习教学的基础知识,而且要学习其它学科的基础知识,并在学科交流中发现共性.
1.2 语言符号学
多特蒙德理工大学的Jennifer Dröse与Götze Daniela利用语言学和符号学理论,对教材内容进行了细致地研究.Jennifer Dröse对德国四年级(小学)、五年级(初中)数学教材中的应用题表述进行了比较研究.她发现,相比于四年级教材,五年级教材应用题中的动词、名词明显增多,导致其语言理解难度与问题情境的复杂度明显增加.为了帮助学生适应小学、初中的衔接,她建议,五年级教师需要重视对于教学内容的准备与编排,以帮助学生尽快适应五年级教材的表述特点.而Götze Daniela利用语言学中意义相关的词汇对教材中图像、文字、符号之间的关系进行了优化,形成新的实验教材,并记录了一位四年级学生使用以上教材的学习过程.研究表明,在学习过程中,意义相关的词汇具有中介作用,可以将具体的或标志性的表征与运算联系起来,从而有助于学生理解.
日本筑波大学的Shogo Murata使用四边形层次分类法[2](de Villiers,1994)的5个维度对两套日本最新中学教材中的几何部分进行了分析.研究表明,以上教材中并没有包含四边形层次分类的所有维度,他建议教材中同一概念需要有多种定义方式,即只从一个维度呈现概念是不恰当的.
1.3 多元表征理论
华东师范大学鲍建生研究团队从ERIC和CNKI上共收集了211篇关于数学表征的文献,发现仅19篇文献是关于数学教材中数学表征的研究.这些文献主要以中小学教材为研究对象,研究关注某一教材的数学表征特点,或者对多本教材的数学表征方式进行比较,研究内容聚焦算术、代数和几何,主要采用文献分析法或比较研究法进行研究.鲍建生认为,随着数字教材和其它形式教材的不断出现,需要加强对教材中数学表征的研究以适应时代的进步,但目前关于数学教材表征的研究还处于起步阶段,研究方法和工具相对简单.
西班牙巴斯克大学的Oihana Moreno-Arotzena等学者借助Hughes Hallett等学者提出的“四法则”理论[3],即概念可以用图像、数字、符号、文字4个角度进行表征,以大学数学教材中的“梯度”概念为例,分析教材中是否均存在相应的任务以帮助学生完成“梯度”概念不同表征之间的转换,从而对教材的质量进行评价.类似地,德国弗里德里希-亚历山大大学埃朗根-纽伦堡分校的Jennifer Postupa提出,可以通过比较教材中图表、注释及任务的数量,以比较不同年代、不同国家数学教材的编写特点.
荷兰Marc van Zantenl与Marja van den Heuvel-Panhuizen学者为发现“现实数学教育”这一思想是如何影响荷兰数学教材的编写,对荷兰一~三年级教材中的加减法内容进行了分析.研究发现,在近些年的教材中,关于阐释加减法运算过程的直观表示越来越具体,这影响了学生对运算的多样化理解,因为学生动手尝试所带来的实践性与开放性是难以被取代的.据此建议,教材在编写过程中应适度“留白”.
2 教材内容的评价
此次会议中,基于教材内容的评价研究是重要议题之一.多位学者在教材内容呈现方式、编排顺序以及研究方法上展示了他们的研究成果.
2.1 内容的呈现方式
学者Allan Tarp以小学数学教材为研究对象进行教材内容的评价研究,他认为:当单词语言作为对外部世界的描述对学生进行外部教授时,数字语言作为其元语言或语法的例证而在内部教授,这使得数字语言更加抽象,难以学习和应用.因此建议:数学教材应进一步引导孩子们掌握“许多”这个概念知识,因为“许多”这个概念涉及比例、微积分、方程和建模等数学核心知识.
巴西Cydara Cavedon Ripoll等学者针对分数的性质、分数运算两部分内容对巴西小学教材进行了分析.研究发现,只在两本巴西教材中明确提及分数相等的判别标准.随着分数学习的深入(巴西六年级),分数等价性问题才能得以解决.
巴西Lourdes M. Werle de Almeida等学者以高等数学教材《微积分第2卷》为研究对象,对教材如何引入二重积分概念的方式进行探究.结果表明,教材引入二重积分概念的方式是通过图表推理呈现的,学生在使用教材的过程中用图表表征自己的认知过程,有利于加深他们对概念的理解过程.
墨西哥Josip Slisko等学者从宏观角度对数学教材中的不合理编排和错误的事实性知识进行了调查.调查结果表明,不清晰的问题和不必要的复杂作图任务对学生的表现会产生负面影响.因此,Josip Slisko等学者建议,如果出版社和教育部的修订程序无法解决墨西哥教材存在的以上问题,教师应设计“合理改变教学顺序、引导学生发现并纠正作者使用的错误公式”等活动,以帮助学生减少其负面影响.
2.2 教材中的数学史
很多教材中出现了关于数学史的介绍.南安普敦大学的范良火与华东师范大学的李楠比较了上海教育出版社、人民教育出版社的两套中小学数学教材中数学家是如何呈现的异同.研究表明,两套教材均介绍了中国与国外的数学家,但是大多数介绍的数学家都是古代数学家,初中教材更加重视对数学家的介绍.但德国学者Sebastian Schorcht指出,大部分教师并没有意识到数学史与数学知识、数学思想方法等的关联,而是简单地利用“数学史”内容提高学生的阅读能力.
2.3 教材评价的方法
在传统的教材评价工作中,往往需要对教材每一页的内容进行详尽分析,这需要极大的工作量.萨姆休斯顿州立大学Dustin L. Jones等学者为了提高分析效率,在参照原有结论基础上,分别采用简单随机抽样、系统抽样、分层随机抽样、整群抽样4种抽样方法以调查统计内容在以上教材中的分布状况,并将抽样结果与全面调查的结果进行对比.研究发现,在以上的抽样方法中,分层抽样后的统计结果误差最小,这将有利于进行大范围的传统教材评价工作.
3 教材的比较研究
在数学教材比较或历史发展方面,国际会议学者不仅关注教材间的横向比较研究,也专注了教材的纵向比较研究.
3.1 横向比较研究
Yasin Memiş等学者对不同国家同一数学内容进行分析与研究.土耳其阿纳多卢大学Yasin Memiş等学者探讨了土耳其、新加坡和加拿大中学数学教材中比例推理的内容分布.结果表明,新加坡教材中比例推理内容所占比例最大,让学生经历较完整的体验比例推理的学习过程,而加拿大和土耳其教材中比例推理内容所占比例较小.因此指出:研究结果为教材编写者和课程决策者提供了重要的反馈.
巴西Franciele Marciane Meinerz等学者对巴西、西班牙与葡萄牙的多部数学教材中方程、不等式内容的呈现方式进行比较.研究发现,三国教材中均使用天平模型帮助学生理解方程概念,但在不等式内容中,天平模型仅作为引入内容.同时,三国数学教材均缺少“帮助学生理解方程与不等式内容之间的联系”的相关数学内容的设置.因此建议,在教材开发中,天平模型不但可以帮助学生更好地理解方程与不等式的相关概念,还可以帮助学生认识此二者之间的联系.
华东师范大学的陈月兰和何晓燕对中国、日本、美国高中数学教材中的三角函数内容及编排特点进行了细致研究.研究表明:3个国家对三角函数的重视程度较高,但中国教材中三角函数的内容最少.在美国和中国的教材中,三角函数的应用设置在三角函数之后,而日本教材则相反.因此建议,单位圆应该作为三角函数学习的有效工具,教师可以利用单位圆的对称性引导学生来探索三角函数公式.
3.2 纵向历史研究
纵向比较主要集中于对不同时期的数学教材进行比较,以发现数学教材的明显特征变化以及数学内容渗透的变化.华东师范大学鲍建生与Hyoungmi Cho着重分析了2009、2015年韩国小学数学教材中在分数除法、分数直观表示上的异同.研究表明,随着韩国数学课程的修订,2015年教材的分数除法内容也强调了情感特征.2009年和2015年的教材都将分数除法分为不同类型的运算法则、概念化和直观表示.2009年的教材打算在逻辑上和程序上提出“乘除法转换法则”.另一方面,2015年的教材旨在激发学生对各种表示的兴趣,如分数除法运算法则和直观表示.
肯尼索州立大学的Tad Watanab对日本两个版本教材中“比、比率和比例关系”内容进行纵向和横向对比.研究表明,虽然比例关系的概念在四、五、六、七年级均有所涉及,但是在每个年级都不断渗透新的数学知识与更高的数学学习要求.并且,日本课程明确区分了不同单位的两个量与同一单位的两个量间的比较问题,这两种类型的比较均在五年级出现.但是在上一次修订中,六年级出现了“单位1”的概念.因此,对该部分内容不同引入顺序的比较在日本数学教育界似乎仍是一个悬而未决的问题.作者建议,扩大分析范围可能会让人们对教材中比例关系的处理有更多的认识.
4 数学教材使用研究
数学教材使用研究始终是数学教材研究领域的热点话题.此次会议中,一些学者采用社会教学四面体(socio- didactical tetrahedron,简称SDT)理论[4],对“学生、教师、资源”之间的互动关系进行了研究.SDT理论模型如图1.
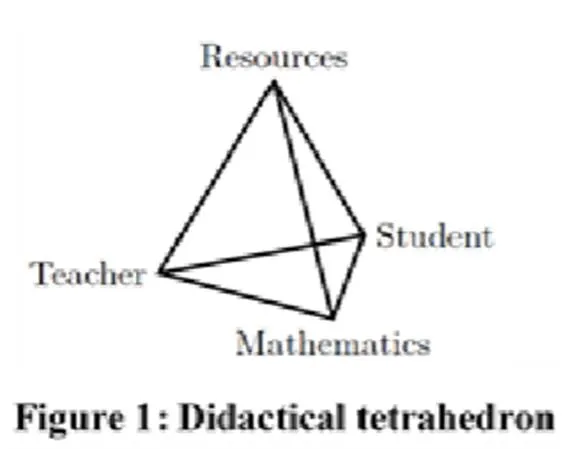
图1 SDT理论模型
4.1 教师与教材的互动
萨格勒布大学的Dubravka Glasnović Gracin与奥西耶克大学的Ljerka Jukić Matić对学生和教师使用教材的方式和原因进行了探究,并着重探讨了影响教师与学生使用教材的社会性因素.从学生和教师两个相互依存的角度进行个案研究,将教学和教材的使用描述为社会过程.结果表明,学生对教材的使用依赖于教师在学生和教材之间的中介调节过程.此外,许多教师关于教材使用的方式会受到教师的社会构成规范的影响.
4.2 学生与教材的互动
美国密歇根大学的Vilma Mesa等学者通过对教材内容进行编码,以调查教师、学生在微积分、线性代数和抽象代数学习中使用数学教材的情况.结果表明,在教材的使用过程中,与其它教材相比,以数学学科能力为导向的数学教材更能促进学生的数学学科能力的提高.在学生学习例题与完成习题的同时,他们在数学思维方式、数学符号的使用、提出和解决数学问题方面有很大的提高.
5 数学教材开发研究
德国波茨坦大学的Thomas Jahnke认为,教材开发中应体现理论基础、实践基础、教学实例与任务实例的融合.
5.1 教材开发的原则
多特蒙德工业大学的Susanne Prediger认为,教材的编写应体现以下原则:(1)支持学生的理解过程;(2)通过合作促进概念理解;(3)引导学生实现“再创造”和“数学化”;(4)在“垂直数学化”中帮助学生进行知识主动建构;(5)在多元表征和不同数学方法间建立联系.
5.2 教材开发的方法
作为丹麦一~九年级数学教材的编写者,奥胡斯大学的Tomas Højgaard认为,理论模型在教材开发上可以起到规划教材的内容结构、确定每一章节的核心能力以及指导每章节内容的呈现方式的作用.在开发过程中,他提出了一个“年级—能力—概念”三维模型以规划教材的顶层设计.在每个年级的教材编写中,所有教学内容都会在这个模型中找到合适的位置(如图2六年级教材所示),以便可以从适当的角度完成对该部分内容的编写工作.六年级教材内容所体现的核心能力在框架中的分布如图3所示.
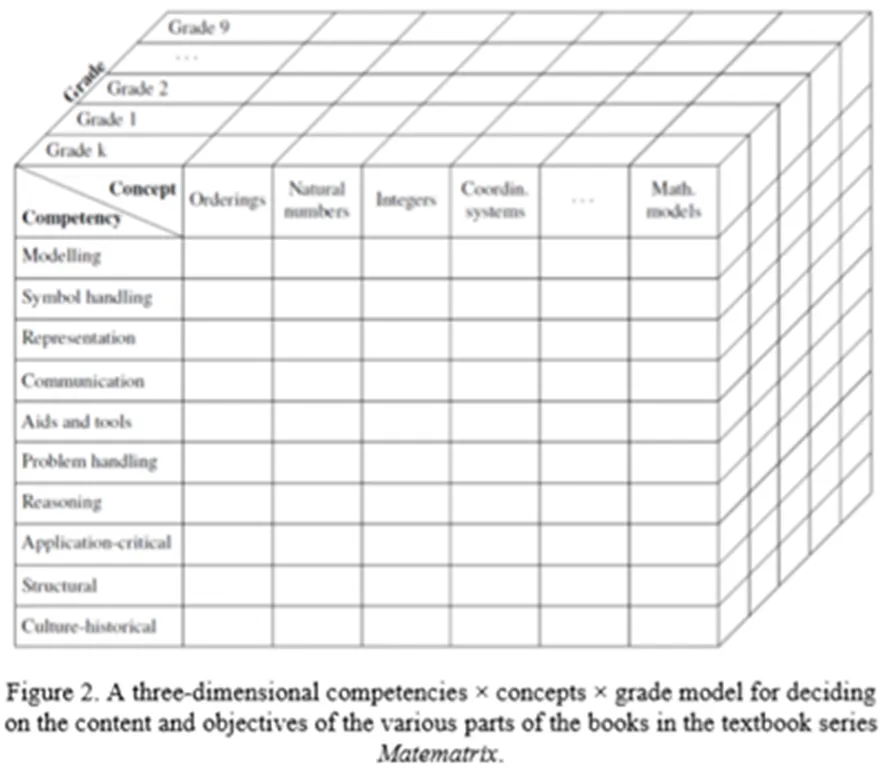
图2 “年级—能力—概念”三维模型

图3 六年级教材内容所体现的核心能力在框架中的分布
作为一种学习理念,“项目式学习”在近10年来被越来越多地应用到学科教育领域,北京师范大学的綦春霞在大会上作“基于项目式学习理论教材的开发与实践”的报告.在理论研究方面,綦春霞团队厘清了数学项目学习的实施标准及评价标准;归纳了当前国际数学教育领域新兴的项目学习模式;明确了项目学习在数学学科中应用路径、影响效应及面临的挑战等;规范了数学项目式课程设计的一般路径,即确定核心概念、明确知识目标、预设知识的发展序列、确定项目主题及任务分割.在实践研究方面,綦春霞团队明确了数学项目式课程的功能定位、基本体例及设计原则等,为后续系统设计项目式课程提供统一规范;以《课标》和教材为参考,系统设计了初中项目式数学课程.研究发现,项目学习课程能够适应初中生的认知风格和学习需求,对于学生数学问题解决、探索创新等能力,学习态度、兴趣等非智力因素的培养有显著的积极影响.
6 基于信息技术的学习工具
数字教材和智慧学习平台也是此次大会的重点议题之一.荷兰埃因霍温理工大学的Birgit Pepin在报告中指出:数字教材可能有助于教育创新,因为它们可以帮助教师在教学过程中实现新的课程意图.同时,数字教材也可能阻碍真正的创新,因为它们限制了教师重新课程设计与开发能力.他认为,除了培训教师恰当地使用资源外,还应综合培养教师的资源开发能力.
6.1 数字教材的开发
相比于传统纸质教材,数字教材在改革课堂教学模式,研究学生学习特点上起到了突出的效果.通过观察学生的行为、参与程度和与同伴的交流,利用数字教材可以判断学生是否深度参与了课堂教学活动.在德国,第一批数字教材在过去的几年里已经出版.随着“资源”概念的拓展,产生了新的教材观念,因此多样化的数字教材也随之发生了结构性的变化.因此德国杜伊斯堡-埃森大学的Maximilian Pohl与Florian Schacht认为,研究者既需要关注数字教材的结构变化,也需要关注学生对数字教材的实际使用情况.
根据美国学者Alden J. Edson, Elizabeth D. Phillips与Kristen Bieda的课堂实践,他们发现在以探究为导向、以问题为基础的数学课堂中,数字教材可以发挥重要的协作特性.首先,在和他人分享交流的过程中,学生可以经历生成、评价、改进自己作业的过程,从而提高自己的表达能力;同时,通过理解他人的作业,可以加深对数学概念的理解.数字教材的协作特性增强了课堂上的社会互动能力,可以提高学生在数学情境中提出问题的能力,树立数学学习自信心.
数字教材还为评价和分析学生在数学课堂中的参与程度提供了新的途径,拥有很大的研究潜力.基于253名六年级学生在3次分数教学活动中产生的日志文件,德国慕尼黑理工大学的Frank Reinhold等学者对以上数据进行了聚类分析,发现了学生体现出4种不同的参与程度.而帕德博恩大学的Sebastian Rezat利用MAXQDA,对多个三年级学生在实验环境和真实环境中使用数字教材的录像进行编码及聚类分析,将学生在教学中的应答模式分成3种类型,并根据学生的使用情况对数字教材的开发提出了建议.
6.2 数字平台的应用
通过视频教程和在线适应性数学活动和游戏来支持数学学习者,以及教师准备课程、选择任务、评估学生的理解和技能,并与同事协作的数字平台在K-12年级和高等教育中十分普遍.会议中对一些数字平台的特点进行了介绍.
美国的动态评估项目(ongoing assessment project)始于2003年.基于对学生学习的研究,OGAP为教师提供了一整套形成性评估工具、资源和使用说明,以帮助他们系统地、持续地在学生的学习路径上回应他们对核心概念的理解.OGAP的评估过程基于评估—分析—回应循环,其框架综合了问题情境、知识结构和学习路径,教师可以利用以上支持来分析学生的作业并确定教学的进一步规划.最近的研究表明,OGAP的使用在学生解决问题的准确性和策略使用上,以及教师对学生思维的理解上有显著的促进作用.
STEP(seeing the whole picture)是一个在线数学形成性评价平台.STEP可以对学生答案进行自动批阅,尤其对于那些基于不同的数学推论,需要学生构建不同示例,具有很强开放性的任务,这里被称之为EET任务(example eliciting tasks).STEP中EET被设计成有许多可能的正确答案,这些答案可以根据不同的特征进行自动分析.其作答分析不但可以为基于学生学习错误的研究或实践提供帮助外,还可以根据学生作答中出现的数学对象的不同特征,分析学生作答的生成过程.在课堂上,STEP可以为教师提供对于学生水平的实时学习分析.
而还有一些研究者重点关注数字平台对教师、学生的影响.美国肯特州立大学的Scott A. Courtney介绍了俄亥俄州的数字平台是如何帮助当地农村地区六~十二年级的数学教师、教学干预专家和大学数学教育研究者在网上协同工作,给予农村学生在数学上的巨大支持,以帮助他们进入大学或者进行职业教育.
在课程改革背景下,法国于2017年开放了两个数字平台(CARTOUN与DRSB).其中,CARTOUN允许教师相互分享教学设计,而DRSB则储存了教师教学所需的大量资源.法国布雷斯特大学的Ghislaine Gueudet对以上两个平台进行了分析和比较.他首先观察教师是如何利用以上两个平台进行教学设计,再去分析两个平台与其它资源、软件的兼容程度.研究表明,可以通过以上两种方式来调查数字平台在教师中的使用状况.
荷兰埃因霍温理工大学的Birgit Pepin与Zeger-Jan Kock从宏观和微观两个层面,对荷兰政府资助的数字教育平台(WIKIWIJS)进行了分析.结果表明,在宏观层面,研究者发现平台支持开放共享资源的创建、修改和使用,这些资源可以链接到平台内外的资源;平台还支持教师共同制作资源;通过将教育相关的元数据附加到数字资源上,增强了平台的搜索功能,从而使教师更容易访问各种存储库和数据库中的资源.在微观层面,该平台可以在一个主题与相关知识、不同概念或不同主题的领域和学科之间建立联系.但WIKIWIJS不提供教师之间,或师生之间的交流平台,也不提供关于学生学习的数据存储(例如,测试结果).研究者认为,该平台有可能改变教师的文档工作习惯.
丹麦奥尔堡大学的Andreas Lindenskov Tamborg和Morten Misfeldt调查了“数字平台”对教师教学的局限与支持.研究者用两个例子说明数学教师在使用这些平台时所受到的启示和约束.结果表明,使用平台的效果取决于教师是否遵循平台的理念和方法.但研究者认为,在平台与教育系统的关系上,各国之间存在着巨大的差异,平台是由国家集中开发的,还是由私人公司开发的?开发这些平台的目的是什么?它们是教师自愿使用的吗?这些问题的答案对数学教师的工作都有着重要的意义.
需要注意,虽然信息技术在帮助学生学习的过程中起到了关键的作用,但也暴露出一定的问题.智利学者Alex Montecino与Melissa Andrade-Molina发现,随着信息技术逐渐渗入智利的课堂,智利教育上的两极分化现象进一步加重.其原因在于,信息技术所发挥的威力取决于他们的使用者,即教师和学生所具有的能力.
7 对中国数学教材研究的启示
由以上分析可知,此次大会对中国数学教育研究有如下4点启示.
7.1 应重视数学教材研究中的理论构建
无论是教材开发、教材内容的呈现、教材的比较、教材的使用等方面,理论框架占据重要的地位.例如,多位学者将ATD理论、四面体理论、符号学理论、项目学习理论应用于教材的分析和开发.另外,在教材与教师、学生之间的关系上,也有专题组进行相关研究.这说明在教学中,教材不是独立存在的,而与其它要素之间存在密切的关系,这在教材开发、使用和评价中都需要重点关注.
7.2 应重视信息技术和数字教材的研究与开发
在此次会议的所有主题中,均包含数字教材的开发、研究和评价,基于互联网的智慧学习平台与数字教材也已经成为热点话题.随着信息技术的发展,科技在数学教育中发挥的作用与日俱增,其不但可以颠覆课堂教学的传统模式,更为中国学者了解学生的数学学习过程提供数据支持,因此数字教材的开发、实验、推广和使用研究应该成为中国未来数学教材研究的重点.尽管信息技术在改变学生学习方式,提高教育公平性上具有重要的作用,但也会加大教育资源两极分化的趋势.以色列海法大学的Shai Olsher指出,教师的水平会极大地影响教师对资源的选择和使用.因此,如何加强教师培训使得教师可以合理地使用教学资源,减少两极分化也是中国数学教育工作者亟需关注的问题.
7.3 应重视不同阶段教材的比较研究
国外学者在教材内容的编排顺序及呈现方式上进行了细致的研究,但这些研究主要集中在小学阶段,中学、大学阶段的教材研究较少,因此建议中国研究者应重视中学数学教材,乃至大学数学教材的研究.在教材编写过程中,编写者应注意不同学段教材间的表述差异,以帮助学生更好地完成学段衔接;在编写过程中,应从多个角度对概念进行定义,并设置相应的任务以帮助学生完成多元表征间的转换.在教材比较上,参会学者不仅关注了教材间的横向比较研究,也关注了教材的纵向比较研究.教材比较研究有助于研究者借鉴不同版本的数学教材的优点,各国教材比较的异同反映了教材在社会文化和功能定位上的差异.对这些差异进行合理、有效的解释,有助于中国更好地开发有利于数学学习的教材.
7.4 应重视教材的动态性与广义性及应用性
南非威特沃特斯兰德大学的Jill Adler在她的主题报告中指出,近20年来数学教育中的“教材(或资源)”在3个维度上发生了重构.一是“资源”由一个名词转变为一个动词,即意味着研究的重心转变为教师在实践中是如何与资源进行互动的;二是“资源”的概念发生了拓展,除了传统的实体教学用具外,网络资源,甚至学生所处的社会文化环境,都可以视为广义的“资源”;三是关于“资源”的理论导向也发生了变化,在学校教学中,更加重视将“资源”与学生的日常生活及动手实践相联系,这些都为研究者更好地看待教材和资源提供新的视角.同时也应该认识教师在教材使用中的关键作用.南非威特沃特斯兰大学的Moneoang Leshota指出,当教师不能完全理解教材编写意图时,教师难以发挥教材在教学中的应用价值.因此建议教材编写人员应加强与一线教师及教研员的交流.
[1] BIKNER-AHSBAHS A, PREDIGER S. Networking of theories as a research practice in mathematics education [M]. New York: Springer, 2014: 76–91.
[2] VILLIERS M D. The role and function of a hierarchical classification of quadrilaterals [J]. For the Learning of Mathematics, 1994, 14 (1): 11–18.
[3] CHANG B L, CROMLEY J G, TRAN N. Coordinating multiple representations in a reform calculus textbook [J]. International Journal of Science and Mathematics Education, 2015, 14 (8): 1 475–1 497.
[4] REZAT S. From the didactical triangle to the socio-didactical tetrahedron: Artifacts as fundamental constituents of the didactical situation [J]. ZDM, 2012, 44 (5): 641–651.
The Review of the Third International Conference on Mathematics Textbooks Research and Development
QI Chun-xia, CAO Chen, FU Yu
(Beijing Normal University, Beijing 100875, China)
The Third International Conference on Mathematics Textbook Research and Development in 2019 mainly included the theory of textbook research, textbook development, textbook content, textbook history, textbook comparison,textbook research, digital textbook and other topics. After analyzing the conference papers and conference speeches, we could summarize the latest views, achievements and directions of international mathematics textbook research, and provide some reference for the research of mathematics textbook in China.
textbook content presentation; textbook comparison; textbook history; digital textbook
G423.3
A
1004–9894(2020)02–0089–05
2019–12–18
北京师范大学未来教育高精尖创新中心项目——中学数学学科诊断分析工具开发与应用研究(BJAICFE2016SR-008)
綦春霞(1966—),女,山东东营人,教授,博士生导师,主要从事课程比较、数学教育研究.
綦春霞,曹辰,付钰.第三届国际数学教材研究与发展会议综述[J].数学教育学报,2020,29(2):89-93.
[责任编校:周学智、陈隽]
