数学学科核心素养导向下的有理数教学实证研究

吴增生

数学学科核心素养导向下的有理数教学实证研究

吴增生

（浙江省仙居县教育局 数学教研室，浙江 台州 317300）

以有理数为例，基于文献研究提出发展数学核心素养的教学策略：以数学核心素养的双向细目表为导向，在数学思想引领下整体设计与数学核心素养相匹配的教学活动．用教学对比实验的方法研究这种教学策略对学生学业水平及数学核心素养发展的影响．通过数据分析发现：在前测和后测显著相关的前提下，实验班和控制班前测数据没有显著性差异，而两次后测中，实验班成绩显著高于控制班．研究结果表明：这种教学策略，对学生学业水平和核心素养的发展，都具有显著促进作用．

核心素养；整体教学；实证研究

1 研究背景

自从林崇德教授领衔的课题组于2016年发布研究成果“中国学生发展核心素养”[1]以来，数学学科核心素养的研究如火如荼，并取得了一系列的成果．一是通过对数学学科核心素养内涵的研究，明确了数学学科核心素养的涵义和主要成分．如，蔡金法、徐斌艳提出了数学学科核心素养的4个成分：数学交流、数学建模、智能计算和数学情感[2]；喻平通过因素分析，得出数学学科核心素养的8个成分：数学抽象、运算能力、推理能力、数学建模、数据处理、空间能力、问题解决能力和数学文化品格[3]；史宁中把数学学科核心素养归结为“会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界”[4]；在《普通高中数学课程标准（2017版）》中，进一步明确了数学学科核心素养的内涵，给出了数学抽象、逻辑推理、数学运算、数学建模、直观想象、数据分析等6个成分，指出了它们之间的关系．二是对数学核心素养的心理机制及教学策略的思辨研究．如，郑毓信提出反对去学科化，要把发展数学学科核心素养落实到学科教学中[5]．常磊和鲍建生则研究了6个数学学科核心素养与情境的关系，发现这些核心素养与情境的关系密切[6]；吴增生研究了数学抽象的认知与脑机制[7]；李昌官研究了数学抽象及其教学策略[8]．喻平提出了发展数学学科核心素养的教学策略，指出“培养数学核心素养需要明确核心素养发展的年龄规律，厘清发展的关键期，需要划分不同的发展水平（知识理解、知识迁移、知识创新），助推从知识理解到知识迁移及知识创新；陈述性知识是核心素养生成的基础，程序性知识是核心素养生成的中介”[9-10]；作为教材编写者，章建跃则研究了教材编写中如何落实数学学科核心素养的发展，提出了“构建数学核心素养双向细目表，明确每一章节和单元落实核心素养的侧重点，制订落实核心素养的操作指南”的策略，他在“指南”中提出“以发展学生的数学学科核心素养为目标，以知识的发生发展过程为逻辑线索，精选学习素材，构建学习情境，设计系列的数学学习活动”，这一观点为将发展数学学科核心素养落实到课堂教学指明了方向[11]．

到目前为止，国内学者对数学学科核心素养的内涵虽仍有一些分歧，但整体上已基本取得共识，对数学教学中发展数学学科核心素养的重要性有了一致的认识，对于如何在数学教学中落实发展核心素养的目标，也有了许多思辨的研究．但是，怎样构建学习情境，设计有效促进学生数学学科核心素养发展的教学活动，形成系统的教学策略体系，并对教学效果进行基于数据的分析评价，这样的实证研究还非常缺乏．基于此，以有理数为例，进行基于数据分析的教学实证研究，探讨具体内容中发展学生的数学学科核心素养的教学策略以及这种教学策略对学生学业水平与数学学科核心素养发展的影响．

2 研究设计

2.1 研究假设

《普通高中数学课程标准（2017年版）》指出，数学学科的核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析，这些核心素养是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，它们既相对独立、又相互交融．这些数学学科核心素养是在数学学习和应用过程中逐步形成和发展的[12]．一方面，数学学科核心素养作为数学思维品质和关键能力，对促进学生学业水平的发展具有重要作用；另一方面，通过适当的教学设计，可以有效发展学生的数学学科核心素养．

研究假设：以数学学科核心素养的双向细目表为导向，在数学思想引领下整体设计与数学学科核心素养相匹配的教学活动，对提高学生学业水平，发展数学学科核心素养具有重要作用．

2.2 设计方案

2.2.1 制作双向细目表

根据喻平的核心素养及其水平分析框架，分析有理数内容相关的数学学科核心素养，制作有理数一章内容的核心素养双向细目表，如表1所示．

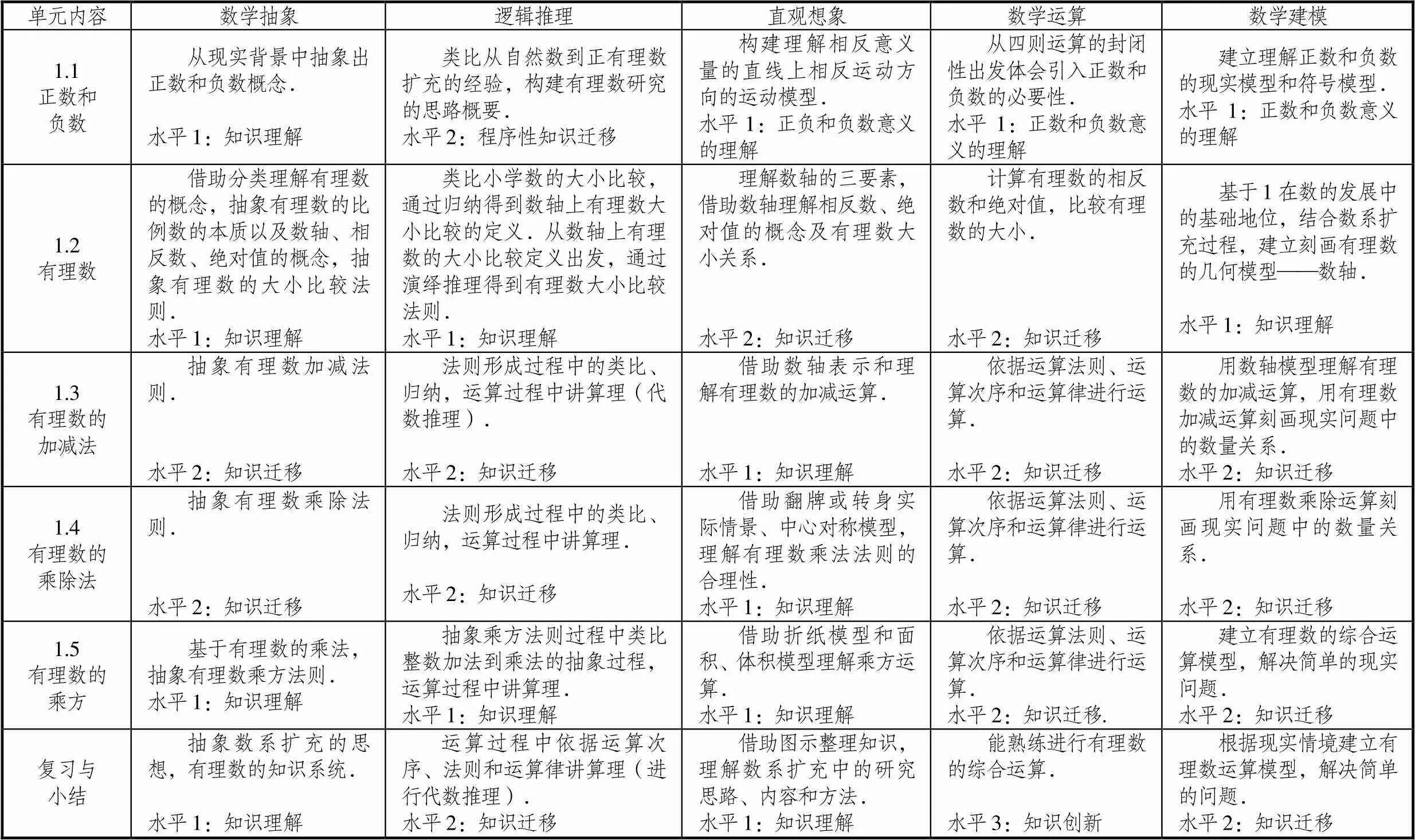
表1 有理数一章的数学核心素养双向细目表（本章没有涉及数据分析素养）

2.2.2 确定教学策略

在数学思想引领下整体设计与核心素养相匹配的数学活动．数学思想是人们对数学的总看法，是一种一般观念（big idea），数学基本思想包括抽象思想、推理思想和模型思想，而数学学科核心素养是具有数学基本特征的思维品质、关键能力及情感、态度、价值观的综合体现，反映的是从事数学活动的能力，并在特定的数学活动中得到发展．这些活动应该具备以下两个条件：一是要有数学思想这个一般观念的统领；二是要与特定的核心素养相匹配．所谓匹配，指的是特定的核心素养所需要的活动步骤和内容（如数学抽象中的“建构模型、分离属性，概括与一般化，定义与符号化，系统化”）．在有理数一章教学中，采用数系扩充这一核心思想引领下整体设计与数学学科核心素养相匹配的活动，是本章的基本教学策略．数系扩充思想包括数系扩充的一般研究思路、研究内容和研究方法，这是总的观念，也是系统结构的抽象．进一步，在有理数的有关概念和法则的学习与应用中，结合具体内容设计与之相匹配的数学活动（直观观察和想象、数学抽象、数学运算、逻辑推理、数学建模中的一种或几种活动）．

（1）整体性教学策略．让学生经历“引入研究对象—界定研究对象，明确研究目标—整体构建研究思路、内容和方法”的整体规划过程，引发学生的目标导向行为，形成问题研究的路径．当这条路径是基于先前经验的总结，又与当前学习内容同步，且在学习小结中再次被总结时，能有效促进学生的学习[13]．在有理数教学中，需要首先引导学生回顾小学阶段数的发展历程（如图1）．在此基础上抽象出数系扩充的研究思路、研究内容和研究方法．研究思路：引入新数，扩大数集—表示新数—研究性质—研究运算和运算律—应用．研究内容：数的性质和运算（包括运算律）．研究方法：特殊到一般，类比，归纳，运算与转化．接着，让学生在相反意义的量的情境中产生正数和负数，并类比小学数系扩充的经验，规划有理数的研究思路、研究内容和研究方法．而在后继教学中，在整体思路下提出问题、分析问题和解决问题．分别研究有理数的定义、表示、性质、运算和运算律．应用研究成果解决简单的问题．

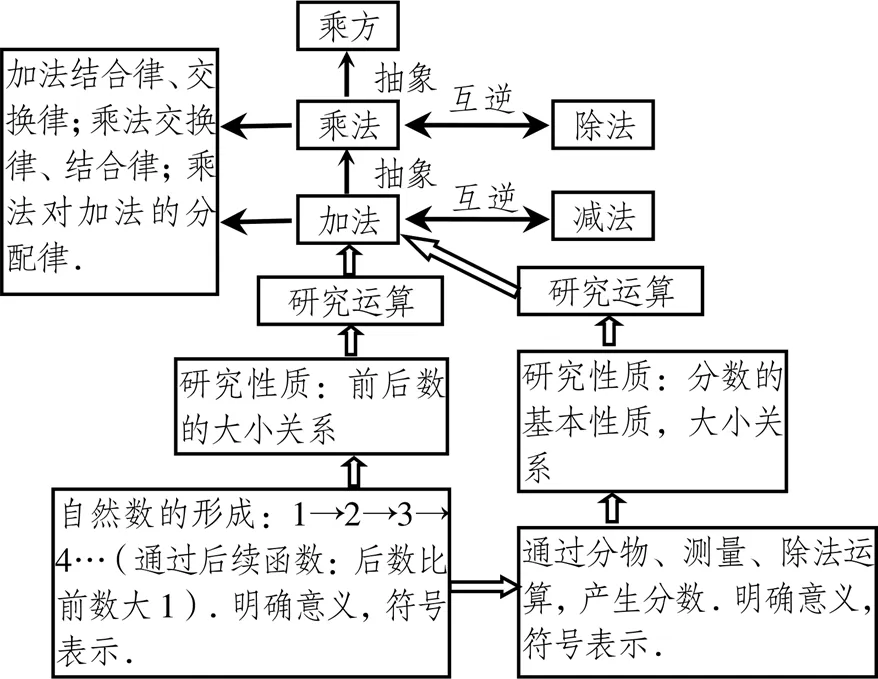
图1 小学阶段数的发展历程

（2）温故知新教学策略．从学生已有知识经验中确定知识生长点，分析知识形成中发展数学核心素养的活动需求，研究与数学核心素养相匹配的活动规律．在此基础上设计数学活动类型和整体活动线索．如上述有理数研究思路的形成过程中，从学生已有知识经验出发，通过抽象形成数系扩充的思路，并迁移到新的数系扩充活动中．在有理数概念的教学中，从学生已认识的有理数的不同类型出发，通过对数的结构（分母是否为1）对有理数进行分类和整合，得到正整数、负整数、整数、正分数、负分数、分数、有理数等概念，在此基础上进一步抽象出有理数的“比例数”本质；在有理数的性质——大小比较教学中，以小学中非负数的大小比较为知识生长点，把这种比较方法投射到数轴上，得到“非负数大小关系”反映在正半数轴上“点的位置关系”的特征——左小右大，并把用这种“左小右大”推广到整条数轴上，借助数轴得到有理数的大小关系的定义；在有理数的运算法则教学中，从小学中的运算法则出发，借助数轴直观和逻辑一致性推广到有理数范围，等等．

（3）根据不同数学学科核心素养相关活动的特点和认知机制开展相匹配的数学活动，让学生在活动中发展特定的数学学科核心素养．根据不同数学学科核心素养的特点和认知机制得到操作步骤，在这种操作步骤的引导下设计与核心素养相匹配的活动，这与喻平的“程序性知识是生成核心素养的中介”的观点一致．

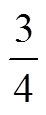
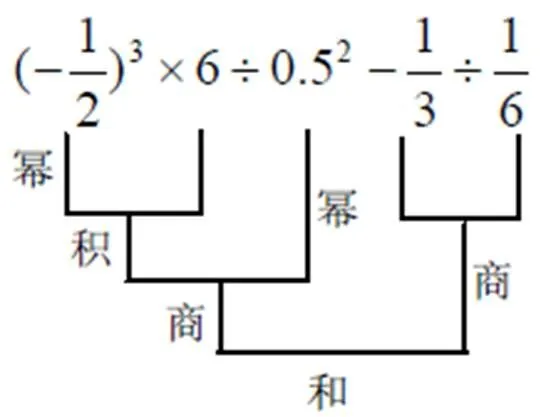
图2 算式的结构分析图

④数学运算的教学策略．有理数的运算是代数运算的基础，因此，本章教学对学生数学运算素养及今后代数的学习，具有奠基作用．有理数内容中发展学生数学运算素养的教学策略是“理解算例、选择算法、准确运算”要求的具体化和活动化：让学生经历运算法则的抽象过程，使其成为他们自己的研究成果，体会其自然合理，深刻理解法则的内涵与本质，加强算理教学；让学生经历从算理控制下的系列加工到自动加工的发展过程，提高运算的准确性；让学生经历依据算理选择和构建算法的过程，发展创新意识；通过适当的运算训练，使运算次序、运算法则、运算律的应用自动化，形成运算技能．

⑤数学建模的教学策略．在知识形成过程中，重视联系现实情境，如在有理数大小比较数轴定义形成后，引导学生思考“这样规定是否符合生活常理？”，借助气温变化理解这种定义的合理性．同时，适当进行用有理数及其运算描述生活中问题的训练，让学生体会用有理数运算模型解决现实问题的过程．

2.3 确定实验变量与实验样本

2.3.1 确定实验变量

确定“基于核心素养的双向细目表，融合数系扩充思想整体设计与核心素养相匹配的教学活动”的教学策略为自变量，以学生的学业水平和核心素养水平为应变量，研究采用这种教学策略对学生学业水平和核心素养发展的影响．为了确定自变量对因变量的影响，以该学校的入学考试成绩为前测数据，设计两个后测，后测1为常规学业水平测试，后测2为与有理数相关的数学抽象、逻辑推理、数学建模、直观想象、数学运算等核心素养水平测试．对3次测试数据进行相关检验，前测数据和后测1、后测2数据的相关系数分别为0.729和0.607，类内相关性检验的Sig值都是0.000．达到显著相关，说明这3次测试具有良好的信度．

2.3.2 选择实验样本

为了验证研究假设，在一所城镇普通初中的七年级16个教学班中选择实验对象．首先用SPSS20.0软件分析入学考试的成绩数据．其中Levene统计量为0.335，差异显著性指标值为0.963；单因素值为0.389，差异显著性为0.941；多重分析结果表明，除了1班和16班外，其余班级之间成绩均值没有显著性差异（≥0.255)．

2.4 实施教学实验

在前测成绩均值没有显著性差异的班级中选择出10个班级，随机选择出七年级（3）班为实验班，其余9个班级为控制班．控制班按照人教版教材编排的顺序和方法由原任课教师实施教学，实验班由研究者执教，按照“基于有理数内容的核心素养双向细目表，融合数系扩充思想整体设计与核心素养相匹配的教学活动”这一教学策略下设计和实施教学，教学时间4周．教学结束时实施后测1和后测2，并用SPSS20.0分析实验班和控制班成绩均值的差异．

3 实验结果

3.1 数据分析

后测1中实验班平均分第一，为80.45分，比控制班的最高平均分高4分．单因素分析中方差齐性分析Levene统计量值为1.724，显著性为0.081；单因素方差分析中方差F值为2.092，显著性为0.029．多重比较结果表明：实验班与控制班的成绩均值差异显著（<0.05）．

后测2中实验班平均分第一，为30.43分（满分50分），比控制班最高平均分高2.03分．单因素分析中方差齐性分析Levene统计量值为1.324，显著性为0.221；单因素方差分析中方差值为7.548，显著性为0.000．多重比较结果表明：实验班与控制班的成绩均值差异显著（≤0.006<0.05）．

数据显示，在前测和两次后测具有显著相关的前提下，实验班和控制班前测平均成绩没有显著性差异，而后测1、后测2实验班显著高于控制班．这说明实验班的教学策略对学生数学学业成绩的提高，特别是数学核心素养的发展，具有显著的促进作用．

3.2 实验结果的讨论

实验的数据分析验证了研究假设，其主要原因可能如下：（1）制定数学学科核心素养双向细目表，明确了具体内容中蕴含的数学学科核心素养及其水平要求，使设计的核心素养相关的教学活动更有针对性；研究数学核心素养的特点和认知机制，得到与之相匹配的数学活动步骤，在此基础上创新教学设计，提高了活动促进数学核心素养发展的有效性；而数学学科核心素养的发展，又促进了学生数学学业水平的提升．（2）在数系扩充思想引领下，整体设计与核心素养相匹配的数学活动，让学生充分经历了数学知识的形成和发展过程，比较深刻地感悟了贯穿有理数知识形成和发展过程中的数系扩充思想，使学生在一般观念引领下建立起系统简约的有理数知识结构，在学习过程中经历了“用相似的方法做不同的事情”的过程，经历了自然合理的数学思考，从而深化了学生的知识理解，优化了学生的知识结构，减轻了学生的记忆负担，促进了学业水平的提升．（3）通过设计核心素养的相关活动，让学生“用相似的方法做不同的事情”，这符合大脑“总是通过修饰已有神经激活模式应对新的挑战”的原理，使学生的数学学习变得简单和自然，提升了学生学习的自信心．

3.3 研究的意义与价值

研究在核心素养相关理论的指导下，制作有理数整章内容中相关数学学科核心素养的双向细目表，研究不同核心素养的特点和认知机制，并在此基础上提出教学策略，尝试在科学理论指导下进行整体教学策略的系统创新，把发展学生的数学核心素养目标落实到课堂教学中；通过设计教学实验，基于数据进行教学实证研究，验证了教学策略对提升学生数学学业水平和数学学科核心素养的有效性．这为今后进行类似研究提供了实证研究的案例．

3.4 研究的局限与展望

因研究是对一所学校的少数样本进行一次性教学比较研究，样本数量不足，需要进行更多的教学验证．今后，需要针对不同内容分别进行多样本的教学实证研究，这样得到的证据更可靠，也能可靠地建立起不同内容的教学策略．这样有助于在教学实践中把发展数学学科核心素养落到实处，更好地体现数学育人的教育理想．

4 研究结论

研究表明，以数学核心素养的双向细目表为导向，在数学思想引领下整体设计与数学核心素养相匹配的教学活动，能有效促进学生数学学科核心素养的发展及学业水平的提高．通过制作数学核心素养双向细目表，明确单元内容知识的发生发展过程中蕴含着哪些核心素养，要达到哪一种水平；通过分析核心素养与数学思想的联系，用数学思想引领，抽象出具有迁移价值的数学一般观念，便于进行学生学习活动的整合设计，让学生在学习中用相似的方法做不同的事情，在思考过程中返璞归真、以简驭繁，在问题的整体思考与研究中形成知识；通过研究不同的数学学科核心素养的认知机制，明确这种核心素养要求学生会从事哪些数学活动及活动过程有哪些主要步骤等，在此基础上整体设计合理有序的教学活动，提高数学教学活动发展特定的数学学科核心素养的针对性．

[1] 核心素养研究课题组．中国学生发展核心素养[J]．中国教育学刊，2016（10）：1-3．

[2] 蔡金法，徐斌艳．也论数学核心素养及其建构[J]．全球教育展望，2016，45（11）：3-12．

[3] 喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1-6．

[4] 史宁中，林玉慈，陶剑，等．关于高中数学教育中的核心素养[J]．课程·教材·教法，2016，36（4）：8-14．

[5] 郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1-5．

[6] 常磊．鲍建生．情境视角下的数学核心素养[J]．数学教育学报，2017，26（2）：24-28．

[7] 吴增生．数学抽象的认知与脑机制[J]．数学教育学报，2018，27（4）：68-75．

[8] 李昌官．数学抽象及其教学[J]．数学教育学报，2017，26（4）：61-64．

[9] 喻平．从PME视角看数学核心素养及其培养[J]．教育研究与评论（中学教育教学），2017（2）：8-12．

[10] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19-23．

[11] 章建跃．高中数学教材落实核心素养的几点思考[J]．课程·教材·教法，2016，36（7）：44-49．

[12] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：4．

[13] 谢和平，安婧，王福兴．多媒体学习中的图文整合：同步化线索和学习者经验的作用[J]．心理科学，2017，40（5）：1 104-1 110．

[14] 史宁中．图形与图形关系的抽象[M]．长春：东北师范大学出版社，2015：184-226．

[15] 周新林．教育神经科学视野中的数学教育创新[M]．北京：教育科学出版社，2016：333-343，427-438．

[16]  DAVID A，SOUSA．心智、脑与教育——教育神经学对课堂教学的启示[M]．周加仙，译．上海：华东师范大学出版社，2013：159-161．

An Empirical Study on Rational Content Teaching under the Guidance of Developing Mathematical Core Literacy

WU Zeng-sheng

(Mathematics Teaching and Research Office, Education Bureau of Xianju County of Zhejiang, Zhejiang Taizhou 317300, China)

Taking the rational number as an example. Based on literature research, this paper puts forward the teaching strategy of developing the core literacy of mathematics: Taking the bidirectional breakdown table of the core literacy as the guide. Under the guidance of mathematics thought Integral Design the teaching activities matched with Mathematics Core Literacy. Use teaching comparative experiment to study the influence of this teaching strategy on students’ academic level and the development of mathematics core literacy. The experimental class adopted this strategy to carry out the whole teaching. The control class was taught according to the textbook arrangement, taking the junior middle school entrance examination results as the pre-test data. after the completion of the teaching, carried out the routine academic level test and core literacy level test as two post-test data, analysis data with SPSS20.0. It is found that under the premise of significant correlation between pre-test and post-test. There was no significant difference between the experimental class and the control class in the pre-test data. But there was significant difference between the experimental class and the control classing in the two post-test data. This study shows that this teaching strategy has a significant role in promoting the development of students’ academic level and core literacy.

core literacy; holistic teaching; empirical study

G622

A

1004–9894（2020）02–0053–05

2019–11–08

浙江省教研课题——基于脑的初中数学总复习教学策略研究（G2019260）

吴增生（1962—），男，浙江仙居人，特级教师，正高级教师，主要从事数学教育研究．

吴增生．数学学科核心素养导向下的有理数教学实证研究[J]．数学教育学报，2020，29（2）：5357．

[责任编校：陈隽、陈汉君]