21世纪国际数学教育在关注什么——基于ICME中TSG主题的分析

陈 昊，王建磐

21世纪国际数学教育在关注什么——基于ICME中TSG主题的分析

陈 昊1，2，3，王建磐1，2，3

（1．华东师范大学 数学科学学院，上海 200241；2．上海市立德树人人文社会科学重点研究基地（数学教育教学研究基地），上海 200241；3．上海市核心数学和实践重点实验室，上海 200241）

每一届国际数学教育大会（ICME）上专题研究组（TSG）的设置反映了国际学术界，至少是当届ICME的国际程序委员会（IPC）对国际学术动态的把握以及对前一届会议实施结果的调整，作为国际学术发展的趋势有一定的参考意义．利用内容分析法，对21世纪以来6届大会（2000年ICME-9至2021年ICME-14）的TSG主题设置进行了历史梳理，并分8个模块进行深入分析，总结数学教育领域的主要研究内容和研究热点，发现了传统主题继续保持，部分主题独立发展，零散主题难以稳定，新生主题有望跻身的特点，最后对ICME-14以及数学教育的发展趋势进行了展望．

数学教育；TSG；主题；关注点

国际数学教育大会（ICME）是数学教育界规模最大、水平最高的国际性学术盛会．第一届ICME于1969年在法国里昂召开，从1972年的ICME-2开始，每4年举办一届．第14届国际数学教育大会（ICME-14）将由华东师范大学与上海市数学会共同承办，在中国上海召开，但受全球性新型冠状病毒肺炎（COVID-19）疫情的影响，原定的会议日期由2020年7月12—19日推迟为2021年7月11—18日．这将是ICME第三次在亚洲举办，也是首次在中国举办，既是一个让国际同行近距离了解和分享中国数学教育的机会，也是中国数学教育学术界可以有更便利的条件去更深入了解国际学术动态，在交流和学习中进一步完善中国自己的教育学科体系的机会[1]，因此可以说此次大会对中国数学教育界的意义非同凡响．广大教育工作者也应该借此机会驻足总结21世纪以来的国际数学教育大会，分析并展望国际数学教育的关注点．

1 从国际数学教育大会看国际数学教育关注点

学术会议最能体现有关领域的最新科研成果，是分析研究热点的重要依据，通过学术会议的交流，可以预测学科领域的未来发展方向[2]．ICME包括诸多学术活动，其中专题研究组（topic study group），简称TSG，涵盖了基本所有的数学教育研究领域，是ICME最主要的学术活动之一，一般通过论文宣读（口头报告）或海报张贴的形式介绍与会代表的一些最新研究成果，广大学者可以在这里跟踪到自己所感兴趣的研究领域的新动向．数量上TSG一共数十个，每组有4~5个来自世界各地的研究者作为协调主持人，会议期间平行举行学术报告．由于大会报告（plenary lecture）和大会团队报告（plenary panel）的数量有限，且报告主题多数由报告人自己选择，因此国际数学教育的关注点，或者说是兴奋点的转变，一定程度上就反映在TSG主题的变化上．广大教育工作者可以通过关注ICME中TSG主题的设置及变化，把握国际数学教育发展动态，明确各个子领域的研究热点并预测其发展趋势．这里对21世纪以来20年间6届ICME的TSG主题设置进行了历史梳理和分模块分析，希望能总结国际数学教育的关注点，从而为数学教育的发展提供客观有效的决策依据和数据支持．

2 研究方法

2.1 数据来源与分类

往届ICME的TSG数据部分可参见会议出版物[3–5]，其它参考当届大会的官方门户网站（http://www.icme-10.dk和http://www.icme11.org）．在ICME-14的第一次IPC会议上（2017年10月10—17日），参考ICME-9至ICME-13中TSG的总结，基于当前一些主题的发展及其它新兴主题的出现，这届IPC成员共同讨论并决定了此次TSG的62个主题和负责团队[6]．在近6届的ICME中，第14届设置的TSG组数之多是空前的（图1）．这里以ICME-14的62个TSG设置为主，将它们按内容分成8个模块，每个模块各自包含一些主题，它们是按照组序号从小到大排列的，不特别考虑主题之间存在交叉的情况．以下将分析ICME-14所设置的TSG主题相较前5届有何变化，从中能解读出这20年来数学教育关注点有着怎样的变化，或呈现出何种趋势．

2.2 研究设计与方法

应用内容分析法，将各届TSG主题内容进行分类，转化为定量的数据，并用定性和定量相结合的方法做出关于事实的判断和推论，说明该领域发展的变动情况，并分析或预判其发展趋势．

图1 近6届TSG组数的变化

具体地，在以下表格中，每个主题前的序号为该主题在ICME-14中的TSG组序号，在前5届的TSG设置中尽量找到与第14届所设主题相同或相似的（以本质内容为主，不细追究前缀后缀等），用●表示；曾经出现过，但不能被第14届组别所替代的主题，便附在与其内容最接近的组下面；没有相同或类似主题的不做标记，为空格．

3 TSG主题的划分与分析

如表1，在对62组TSG的划分中，前5个模块所含的主题数相差不多，也比较稳定，基本属于传统的数学教育研究领域．这里的稳定指的是包括第14届在内，不间断地出现至少4届．新主题指的是自第14届完全新提出的，之前从未出现过．前5个中，模块四最稳定，全部主题都连续4届及以上，且没有提出新主题．模块六涵盖的内容最散，课程、教材、评价、测试、竞赛各占一个主题，也没有新主题的加入．模块七所含的主题数不少，但稳定性很差，8个主题中有7个都是只从ICME-13才开始提出，第14届保留的．内容最少，也最不稳定的是模块八，它既没有主题传承得很好，也没有新鲜的元素注入．下面将依次分析各个模块中的每个主题，追溯历史，洞察变化，展望未来．

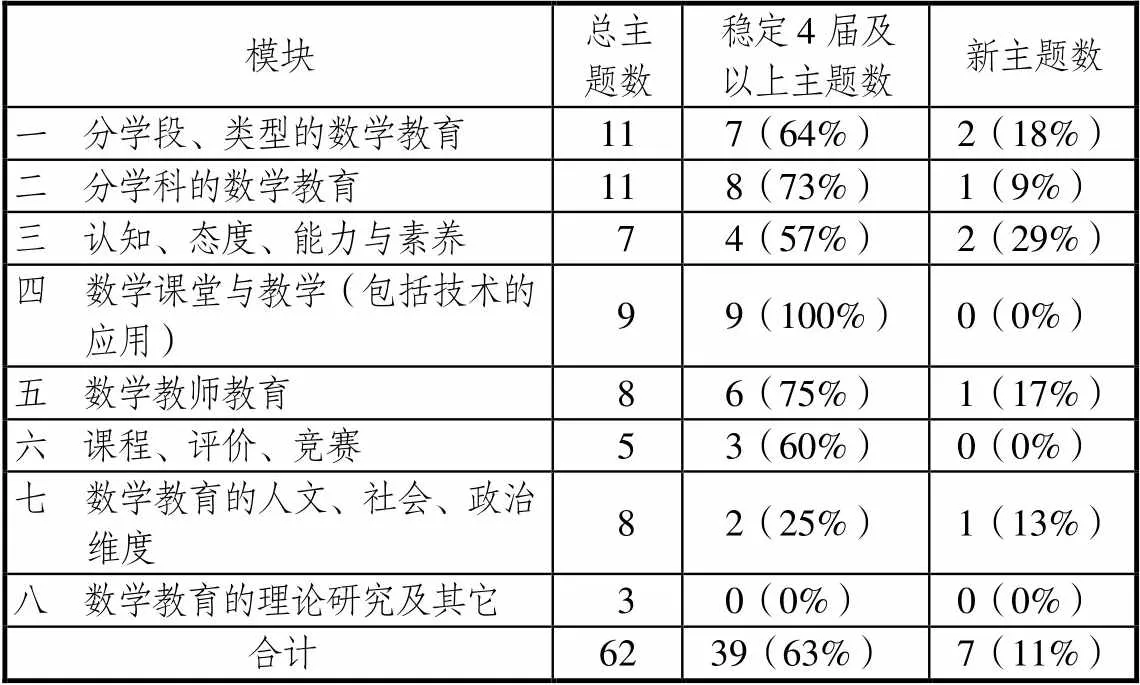
表1 8个模块的基本情况统计

3.1 分学段和类型的数学教育

模块一主题统计如表2所示．

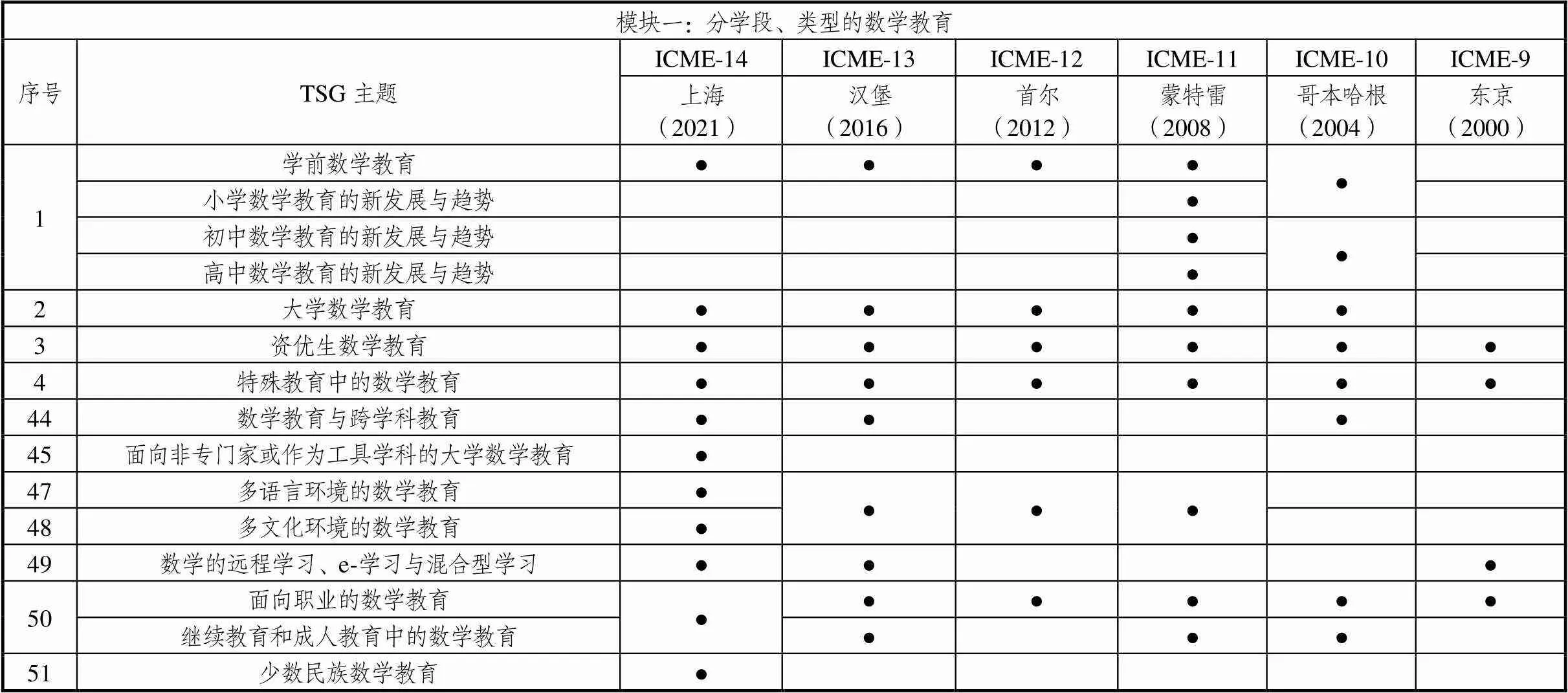
表2 模块一主题统计

分学段教育的主题设置近3届稳定在“头”和“尾”．“头”即指学前，“尾”即指大学（不包括研究生的数学教育）．特别的，ICME-10将学前和小学放在一个模块，初中和高中放在一个模块，ICME-11时将这4个学段都分开，在发现这种分法承载的内容太多之后，近3届都拿掉了中小学的数学教育这类大的主题，放入分学科学段的数学教育（见模块二）．

资优（英才）与特教的两个极端情况被持续关注．比较遗憾的是，国内对于这两个部分的关注和研究都甚少．在CNKI上检索以“数学资优生”为主题的国内文献，不足30篇（截至2019年10月10日）．巩子坤等指出，中国的资优生教育仍存在很多问题，不仅迫切需要加强相关的教育法规和政策建设，还应加大资优生师资培训的力度，因为中国当前中小学资优生教育师资队伍很大一部分是奥数教练[7]，但是对资优生的教育不应局限在培养他们参加竞赛（尤其是竞赛技巧）这方面．同样检索以“数学特殊教育”为主题的文献，不足50篇．田寅生等早些年已经指出了特殊儿童数学教育研究整体水平不高及问题的主要表现[8]，但近年来依然没有该方面较好的研究成果，学校资源不足，学生差异较大，专业人才缺乏的状况依然存在，在解决了这些基本条件之后，怎样让这些特殊团体恰如其分地学习数学是数学特殊教育工作者需要着重考虑的事情，而不单单是关注他们如何正常地生活、融入社会．以上这两个主题（TSG3、4）连续出现6届没有变动，证明全世界都在持续关注这两个层面，因此需要做更多的努力来弥补这里的短板．

跨学科和作为工具学科的数学教育主题近年在升温．2014年第38届国际数学教育心理学（PME-38）和第36届北美数学教育心理学（PME-NA36）联合大会的主题就是重视跨学科与地域的数学教育[9]．STEM课程的出现也是跨学科数学教育的一个非常好的体现，它包括科学（science）、技术（technology）、工程（engineering）、数学（mathematics）．2016年中国教育部出台的《教育信息化“十三五”规划》中也明确指出，应有效利用信息技术推进“众创空间”建设，探索STEM教育、创客教育等新教育模式．

多语言、多文化环境的教学从ICME-11开始逐步得到重视，ICME-14将其分成两个主题．此外特别强调了少数民族数学教育（TSG51），将它首次作为一个独立的主题出现．在美国和欧洲一些国家没有明确提出少数民族的数学教育，而是将其归在多语言或多文化数学教育中，或者归在民族本土数学中（模块七TSG52）．中国西南的少数民族数学教育很有特色，多年来积累了一定的经验，也取得了丰富的研究成果[10]，此外西藏、新疆、内蒙这些地方的数学教育也采取了一些特殊的做法，包括教材、语言等．因此，单独把少数民族的数学教育当作一个主题，是希望能在这个方面做出中国自己的特色，从经验中提炼出有价值的内容．

3.2 分学科的数学教育

模块二主题统计如表3所示．

表3 模块二主题统计

中小学算术、代数、几何始终是关注的核心，它们TSG的设置在学段区分上逐渐细化．关于度量（面积、体积、距离等），它在西方课程体系中大多独立于几何与代数，形成独立的学科，但它作为TSG主题的单独设定近3届才出现．对于中国的数学教学来说，虽然目前很难把度量从几何中分解出来，但已经有专家学者提出了度量的重要意义，并关注到如何在小学数学教学中使学生分清两类度量的本质特征，感悟度量单位所蕴含的数学思想[11]．

概率与统计主题设定的历史较长，且统计先于概率，在ICME-9就出现了．2003年，中国教育部颁布的《普通高中数学课程标准（实验）》中指出，“让学生体会统计的作用和基本思想及了解随机现象与概率的意义”；2017年的《普通高中数学课程标准（2017年版）》将数据分析素养作为数学六大核心素养之一，并进一步指出，统计与概率部分的教学中应着重发展学生的数据分析素养[12]．国内也有学者做了概率与统计这部分教材内容的中外比较研究[13–16]，但这样的研究也不多，也不全面；结论多是中外各有所长，应取长补短，除了内容上的设置，更需要结合好自身优势的同时利用信息技术辅助该方面的教学．总之，这两个学科需要更多关注与努力，使中国的统计与概率教育能够进入到国际层面进行对话．

微积分持续关注，对离散数学的关注次之，有间断．微积分是大学数学教育中非常重要的一部分，这一点毋庸置疑，虽然微积分在国内高中教材上的出现可追溯到1958年，但多年来历经诸多波折变动，广大研究者对它的重视程度仍然远少于其他一些发达国家和地区．在2017版课标中，选择性必修部分只有“一元函数导数及其应用”这个单元涉及微积分，另外它出现在选修A类、B类、E类课程中[17]．尽管其重要性早已明确，国内诸多学者也已经在关注如何衔接大学与高中的微积分部分，但如何将微积分教学落实到高中课堂仍然是亟待解决的问题．

高等数学专题的教与学的主题仅在ICME-10与ICME-11出现，现在这方面的研究被归在了TSG2“大学数学教育”中．

编程与算法是第14届新添的主题，当前国际上较为关注这一方面，但其是否有可持续性尚待检验．在这一主题上，中国可能走了回头路，因为编程与算法曾被列入2011版高中数学课程标准，但是在2017版新课标中又被取消，问题在于如何平衡这一部分内容在教材、教学与考试3者之间的关系．

3.3 “认知”“态度”“能力”与“素养”

模块三主题统计如表4所示．

持续关注的主题有4个：“推理、论证与证明”“问题解决”“数学学习与认知”“数学应用与建模”．它们始终是关注的核心，但其中前3个主题都有发展与变化：在ICME-9时对“推理”的关注还没明确提出，实际上推理的范围更广，是论证和证明的前提，一些新的数学想法的出现在达到论证层面之前，都需要推理；在持续关注“问题解决”的基础上第14届新添了“问题提出”，提出问题可能比解决问题更难，既然是从这届新加的主题，因此，非常希望中国在这方面可以有经验体会和理论与世界共享；数学学习与认知的研究在第14届拓展到对神经科学/认知科学的关注，希望能将客观的神经科学、认知科学的理论用在中国学者对学生数学认知方面的研究上．在“数学应用与建模”这个主题上，也在积极努力地追赶国际步伐，数学建模活动已经正式纳入2017版高中数学课标的必修与选择性必修部分，且中国香港在2019年7月21—26日成功举办了第19届国际数学建模教学与应用会议，这都标志着建模在中国数学教育中（尤其是中学）的地位稳固提升，当下存在的问题仍然在操作和执行层面，可能需要组织一些研讨班，对中学数学建模怎么教进行研讨，旨在提高中学生普遍的建模水平，而不仅仅是培养建模竞赛代表队．

表4 模块三主题统计

学生的情感方面，即数学学习的非认知因素在ICME中有被关注，但不是持续性的．

数学素养在近3届会议上都得到关注，这届更强调不同层级和类型的素养．数学素养以及数学核心素养，近3年在国内的热度增长非常快，期待这次可以在国际平台上交流讨论、学习借鉴．具体地，ICME-12与ICME-13均用literacy这个单词表达广义的素养．经这一届IPC的认真讨论后，分别用3个词去表达素养：competency指广义的素养，literacy指在数学语言阅读、阅读理解或表达方面的素养，numeracy指数与运算方面的素养．

3.4 数学课堂与教学（包括技术的应用）

模块四主题统计如表5所示．

表5 模块四主题统计

对教与学中技术的应用（包括信息化意义下的可视化）的关注，ICME-10是个分界线，之前关注的基本是传统的教具、学具与媒介．教与学中技术应用的学界关注度越来越高，之前是不分学段或拆分成“教”与“学”，发现这样都会导致一些困难之后，从近两届开始分学段，每个学段有它的特色，发展非常快．尽管这一部分体现在TSG主题上的稳定性很高，但是随着科技的发展，它们在内容上是一定有很大变革的，这种变化也是可以切身感受得到的，具体研究可参考TSG论文．

“课堂的实践研究”与“任务设计与分析”之前已出现3届，这届把“课堂的实践研究”细分为小学和中学两个学段，是因为有关这一主题的论文增长速度比较快，是一个发展趋势．

“课堂语言与交流”与“数学史（HPM）的角色”从ICME-10开始得到持续重视．数学教学的创新途径在ICME-10出现过一次，但是后来销声匿迹，也许融合到其它地方．刘兰英曾提出课堂教学的终极追求是为增进学生思维而对话[18]，她还提出了数学课堂师生对话分析的内容框架，包括数学课堂师生对话分析的3个维度与其内含的10个核心要素[19]，为国内这一主题的研究做出了诸多贡献，但放眼国际，中国学者在这一方面的关注度仍然不够，毕竟从十多年前国际上就开始关注这个方面了．中国的HPM研究起步较早，几乎与ICME-10同步，近年来热度升高尤其快，希望这一届中国学者能拿出好的成果到会上交流．

3.5 数学教师教育

模块五主题统计如表6所示．

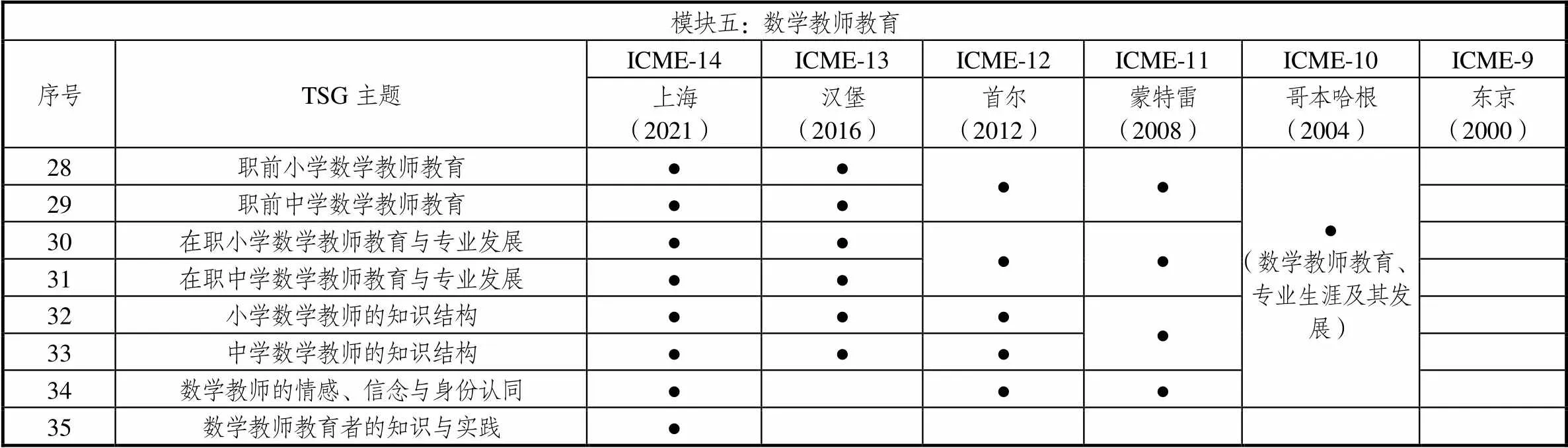
表6 模块五主题统计

教师教育类（包括教师知识结构）的主题经历了从无到有、从粗到细的演化和发展过程．ICME-10只有一个总括的主题，然后走向“职前”与“在职”的分离和“知识结构”主题的单独存在，再走向学段上的细分．教师的情感、信念与身份认同从ICME-11开始间或得到关注．吴颖康基于ICME-11至ICME-13的相关报告和论文分析了数学教师教育研究的现状和趋势[20]，对此模块的发展梳理及预测有很大的借鉴意义．ICME-14的第三调查小组（survey team 3）也是与此模块内容密切相关的：教师的集体工作——为教师发展而存在的学校常规活动（teachers’ collective work as a regular school practice for teacher development）．由此可见国际上对数学教师教育的重视．

东方文化很大程度上影响了这一大类主题的发展，例如日本的课例研究和教学方法，它以开放式案例的形式不断发展并为人所知，且有雄厚的师资队伍作为支撑，如今成为引起全球广泛关注的主题[21]．相比之下，中国在推广自己的教学文化与优势这方面就内敛许多．中国教师教育实践重视高等学校（U）、地方政府（G）、中小学（S）“三位一体”联合培养教师的教育模式[22]，在政策领导下，多年来教师整体水平高，知识结构好，有教学中的朋辈互助，也有老教师对新入职教师的指导，加上教研制度开始于20世纪50年代，经过六十多年的发展，使得中国已经拥有了一支超过10万人的教研员队伍，发展成了省、地市、区县、乡镇、校教研网络（四级教研网络），形成了有效的、体系化的教研工作机构和工作机制，在中国基础教育发展中扮演着关键“角色”[23]，这些都是数学教育中非常有特色的东西．因此，在该领域中国研究者有足够的发言权，应该在这个模块上响亮地发出中国声音，让中国的经验走向世界．

另外值得一提的是，“教师教育者”本身在这届成为一个新的、颇具特色的主题，或许跟中国对这个角色的普遍关注有关．在西方的理念里，教学职责划分很清，被他人指导或指导他人都是不可思议的．教师教育者是教师教育知识的生产者、教师专业发展的引领者以及教师教育文化的推动者[24]．尽管当前中国教师教育者存在身份困境，但已有学者提出教师教育者可以通过建立明确的自我意识，增强身份的实践感和效能感来解决此问题[25]．TSG35关注的即是数学教师教育者本身的知识与实践，并不是教师教育者如何“教”他人的问题，研究者对该组的研究与汇报满怀期待，更希望中国能在这一主题建立起自己的话语体系．

3.6 “课程”“评价”“竞赛”

模块六主题统计如表7所示．

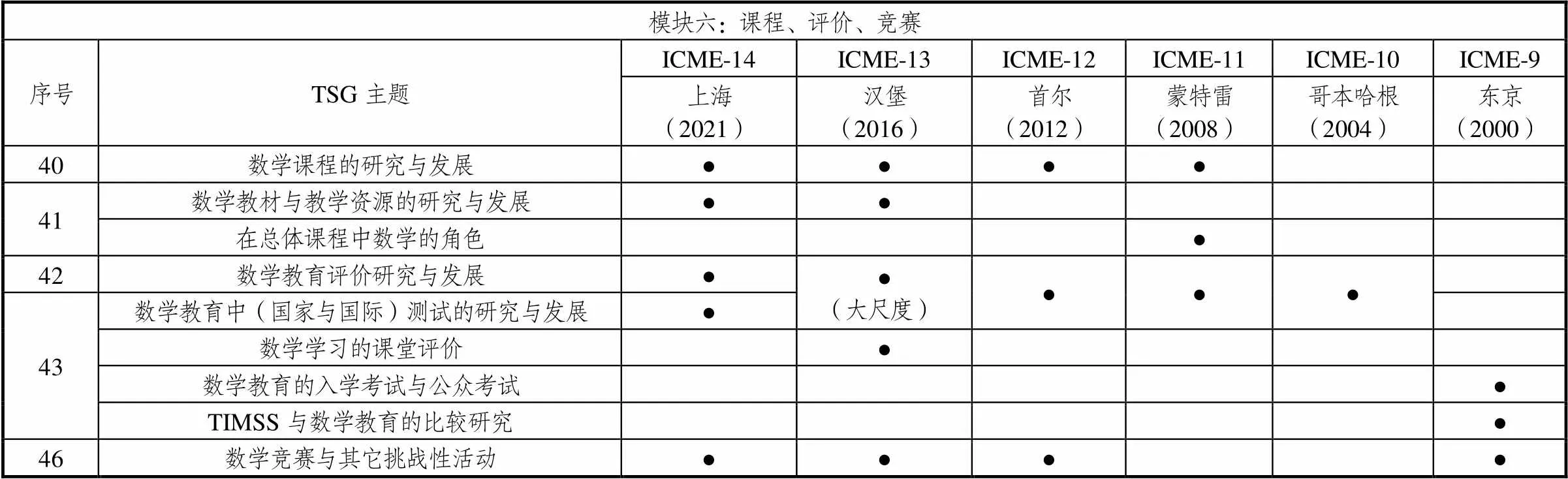
表7 模块六主题统计

课程与教材的研究与发展从无到有，自ICME-11以来进入视野，但是到ICME-13，教材与教学资源才作为单独的主题出现．而早在2011年，中国华东师范大学就成功召开了中小学数学教材国际研讨会，成为该系列会议的发端；2014年，由范良火教授主导的首届数学教材研究与发展国际会议在英国南安普敦大学召开；而后的第二、三届分别于2017年、2019年在巴西和德国召开．以这样的发展趋势来看，教材与教学资源的研究必将成为数学教育研究的一个重要领域．

ICME对考试、测试的关注先以对具体项目的研究形式出现，后转为包容性更大的评价与测试主题，比较聚焦于评价研究．ICME-14将两个主题各自单列，评价研究与发展不管大小尺度都放在一起，而测试更关注于国家和国际层面，似乎是对ICME-9两个主题的回归．ICME对竞赛等活动的关注出现过间断，但近3届保持稳定．

3.7 数学教育的“人文”“社会”“政治维度”

模块七主题统计如表8所示．

表8 模块七主题统计

这一模块总体上的稳定性不高，其中有一部分主题是近两年才被提出．民族本土数学（ethno-mathematics）是巴西数学家和数学教育家达布罗西欧（Ubiratan D’Ambrosio）提出的概念．在ICME-9上以他为组长的TSG对此有深入的探讨，但此话题沉寂了两届，而后重新被挖掘；数学教育中的平等一直是一个重要话题，但有3届会议聚焦于性别平等，近两届研究者关注了更多方面的平等；数学教与学的历史长期被关注，是非常稳定的；ICME-9关注了亚洲国家数学教育问题，实际上地区性的论坛在各届会议上或多或少地被关注，不过这些活动不是以TSG的形式出现；第14届特别强调了数学教育的国际合作，作为一个全新的主题出现，希望可以更好地促进国际交流，互相学习借鉴．另外，数学教育的政治、社会（包括数学普及）与哲学（包括符号学）维度都是从近两届开始特别予以关注的，推测在今后的大会中会持续出现．

3.8 数学教育的理论研究及其它

模块八主题统计如表9所示．

表9 模块八主题统计

关于数学教育理论的TSG主题的设定从ICME-9关注单一的建构主义，到ICME-11对研究新趋势的思考，发展到了近3届对理论多样性的包容．近两届对数学教育研究中的实证方法给予特别关注，这方面在近年来非常被看重，也是尤其需要加强的，一方面，因为中国数学教育相当数量是经验决定的，需要用大数据说明数学教育实践的普适性，另一方面，实证研究的理论和规范都有待明确，应该用更精准的研究给出更能令人信服的结果，而不是为了证实一件已经构想好的事情去“补”上一个实证研究．近两届还关注了数学与创造性；早期的ICME还对数学教育的学科定位、发展趋势以及数学发展在数学教育中的反映给予关注．整体来看，这一模块的内容分散，稳定性最差，这届也没有新提出的主题．

4 结论与讨论

4.1 传统主题继续保持

模块一、二、四、五是多年来的研究重点和热点．这些模块在主题内容上都比较稳定，被视为“传统研究领域”，只是随着时间的进展，有些主题被拆分，从粗化走向细化；有些主题被合并，从细化走向粗化．其中值得一提的是TSG44和TSG49，含数学在内的跨学科教育与混合型学习等，现在来看尚不属于传统领域，但一定是未来稳固的发展趋势，这不仅是对数学教育研究领域的丰富，更是培养以数学为基础的全方位社会有用之才的必然条件．

4.2 部分主题独立发展

模块三、六所含有的主题独立性都很强．例如认知（心理学）、建模、教材、竞赛等，都是相对专一而又独特的领域，它们也有属于自己领域的国际盛会，因此在ICME中，这些领域虽然会一直保持存在，但每个只占一组主题，尽管它们自身内部包罗万象．

4.3 零散主题难以稳定

模块七、八含有诸多零散的主题，这些主题稳定性差，也难以预测发展趋势．人文、社会与政治的层面几乎会影响到所有学科的发展，数学自然也不例外，因此这些主题的存在是十分合理的，研究价值也是不言而喻的．问题在于如何开展这些方面的研究，是否有高水平的成果可以在国际舞台上交流展示．例如TSG58，虽然在做研究时倡导多用实证的方法，但是单纯研究数学教育中的实证方法与方法论又如何？如何能让这样的成果更有说服性，促使各类相关研究更规范？

4.4 新生主题有望跻身

ICME-14相较前几届的大会，TSG组数最多，其中13%（8/62）的主题是上一届新提出，这届“传承”下来，还有11%（7/62）的主题是这一届新提出，是否能够延续下去还有待检验，需要看实际的参与度和后续的反响．在新提出的主题中，大致可分为3类：一类是与中国特色或多或少有关，如TSG35数学教师教育者的知识与实践，TSG51少数民族数学教育，由于每届大会的举办国家或地区都会不可避免地在一定程度上影响到会议的部分内容设置，因此不确定这两个主题是否还会延续到下一届，从另外一个角度说，中国的学者需要在这两个主题上发出更多有力的声音引起世界的注意，从而可能将它们留存在数学教育的世界舞台上，而不是昙花一现；第二类新加主题是与科学的进步和社会热点密不可分的，昭示了研究的新趋势，如TSG14编程与算法的教与学，TSG21神经科学与数学教育/认知科学；第三类是只与数学教育研究内容有关，作为对之前大会的主题补充，如TSG17数学教育中的问题提出（与问题解决合并在一起），TSG45面向非专门家或作为工具学科的大学数学教育，TSG61数学教育的国际合作，这3个领域的研究热度近年都在上升．

4.5 总结与展望

4年一度的国际盛会，如同一场不早不晚的饕餮盛宴，既能给广大研究者带来新鲜前沿的思想碰撞与交流，又是一次绝佳的驻足总结及反思的机会．总结21世纪以来6届ICME中的TSG主题，带来的收获依然是包含“历史”与“未来”两个篇章：历史让研究者们有迹可循，保持清醒——传统与独立的主题将会继续进行，大家可以去填充它、丰富它；未来让大家充满期待，奋力研究——对于零散的主题，剑走偏锋的坚持不失为一种好的选择，对于新生主题，把握机遇、紧跟形势乃是明智之举．

ICME-14已经箭在弦上，中国作为这届大会的东道主，给了中国数学教育工作者一个非常有利的接轨世界的条件与机会．而中国数学教育的发展就如同会议从申办到筹备承办的过程，即便起步晚了一些，即便前路依然充满着困难与考验，但是中国学者肯克服、愿努力、能学习、会总结，最后一定可以给世界呈现一个精彩的ICME-14，也同样可以给世界呈现一个数学教育强国．

由于ICME-14原定会期的推迟可能导致一些事宜的变动，最新消息敬请关注大会门户网站www.icme14.org

[1] 李海，张晋宇，王建磐．承办ICME-14是中国数学教育崛起的良好契机——王建磐教授访谈[J]．数学教育学报，2018，27（6）：55–59．

[2] 邱均平，刘国徽．从学术会议的视角看学科研究热点[J]．情报科学，2015，33（9）：3–7，32．

[3] HIROSHI F, YOSHIHIKO H, BERNARD R H, et al. Proceedings of the ninth international congress on mathematical education [C] // Dordrecht: Springer, 2004: 292–368.

[4] CHO S J. The proceedings of the 12th international congress on mathematical education [C] // Dordrecht: Springer, 2015: 379–583.

[5] KAISER G. Proceedings of the 13th international congress on mathematical education [C] // Dordrecht: Springer, 2017: 373–631.

[6] ICME-14 LOC MEMBERS. The handbook of the first IPC meeting for ICME-14 [C]. Shanghai, 2017: 1–60.

[7] 巩子坤，何声清，殷文娣，等．美国数学资优生教育：是非与评述[J]．数学教育学报，2018，27（2）：29–37．

[8] 田寅生，方俊明．特殊教育学校数学教师知识结构：现状、成因及对策研究[J]．中国特殊教育，2010（4）：62–68．

[9] 刘舒，王光明，王兆云．数学教育的边缘：重视跨学科与地域的数学教育 关注弱势群体的数学教育——PME38和PME-NA36联合大会会议综述[J]．数学通报，2015，54（6）：5–10，33．

[10] 张定强，蒋会兵，蔡娟娥．中国少数民族数学教育研究的回顾与展望——基于1993—2013年CNKI期刊数据的分析[J]．数学教育学报，2015，24（1）：69–74．

[11] 娜仁格日乐，史宁中．度量单位的本质及小学数学教学[J]．数学教育学报，2018，27（6）：13–16．

[12] 朱亚丽，张慧慧，刘月．高中数学新旧课标中概率与统计内容的比较研究[J]．教学与管理，2019（6）：77–80．

[13] 孙露．中新两国小学数学教科书“统计与概率”内容的比较——以PEP版与MC版为分析对象[J]．江苏第二师范学院学报，2018，34（4）：108–114．

[14] 赵凤．中英小学数学“统计与概率”内容比较研究[D]．上海：华东师范大学，2019：1–91．

[15] 王倩倩．中美高中数学概率部分的比较研究[D]．石家庄：河北师范大学，2019：1–61．

[16] 金黎．中澳高中数学教材概率与统计内容的比较研究[D]．武汉：华中师范大学，2018：1–23．

[17] 史娇．基于普通高中数学课程标准（2017年版）下微积分内容探究及教学研究[D]．济南：山东师范大学，2019：1–54．

[18] 刘兰英．为增进学生思维而对话：课堂教学的终极追求[J]．外国中小学教育，2012（7）：58–61．

[19] 刘兰英．数学课堂师生对话分析的内容框架构建[J]．全球教育展望，2013，42（5）：91–99．

[20] 吴颖康．数学教师教育研究的现状和趋势——基于对近三届国际数学教育大会相关报告的分析[J]．中学数学月刊，2016（6）：1–4．

[21] 张佳宁，代钦．日本数学课例研究之启示[J]．内蒙古师范大学学报（教育科学版），2017，30（11）：140–144．

[22] 李中国．两种“三位一体”教师教育模式比较研究[J]．教育研究，2014，35（8）：113–117．

[23] 本刊编辑部．教研转型[J]．人民教育，2016（20）：12–13．

[24] 康晓伟．教师教育者：内涵、身份认同及其角色研究[J]．教师教育研究，2012，24（1）：13–17．

[25] 赵明仁．教师教育者的身份内涵、困境与建构路径[J]．教育研究，2017，38（6）：95–100．

What Is International Mathematics Education Focusing on in the 21st Century——Based on the Analysis of TSG Topics in ICME

CHEN Hao1, 2, 3, WANG Jian-pan1, 2, 3

(1. Department of Mathematics, East China Normal University, Shanghai 200241, China;2. Shanghai Research Base for School Mathematics Education, Shanghai 200241, China;3. Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Shanghai 200241, China)

The setting of Topic Study Group (TSG) at each International Congress on Mathematical Education (ICME) reflects the international academic communities, at least the International Program Committee (IPC)’s grasp of international academic trends and the adjustment of the implementation results of the previous session, which is of certain reference significance as the trend of international academic development. This paper uses the content analysis method to sort out the TSG theme setting of the six conferences since the 21st century (ICME-9 in 2000 to ICME-14 in 2021), and conducts in-depth analysis in eight modules to summarize the main areas of mathematics education. By summarizing the research content and hotspots, we have found that the traditional themes continue to be maintained, some of the themes develop independently, the scattered themes are difficult to stabilize, and the new themes are expected to be in the whole. Finally, the development trend of ICME-14 and mathematics education is prospected.

mathematics education; TSG; topic; focus

G40–059.3

A

1004–9894（2020）02–0041–08

2019–11–22

国家自然科学基金——第14届国际数学教育大会（11942110）；上海市教育委员会——立德树人人文社科基地建设（含课程方案和课程标准修订）（2019基01–01–22）；上海市科学技术委员会——上海市核心数学和实践重点实验室建设（18dz2271000）

陈昊（1995—），女，吉林松原人，博士生，主要从事数学教育研究．

陈昊，王建磐．21世纪国际数学教育在关注什么——基于ICME中TSG主题的分析[J]．数学教育学报，2020，29（2）：4148．

[责任编校：周学智、张楠]