例谈探究式解题课教学

朱清波，曹广福

例谈探究式解题课教学

朱清波1，曹广福2

（1．广州市执信中学，广东 广州 510090；2．华南农业大学，广东 广州 510005）

阐述了解题课的基本功能，指出了目前中学数学教育中解题课存在的问题．通过对一道平面几何题的分析，讨论了解题课环节如何创设一系列探究式问题，引导学生从问题的条件出发通过特例、试错等方法猜测一般规律并找到解决问题的方法，反思是如何想到这样的方法的？进一步对解题方法的优劣进行评判．通过方法的探究过程培养学生的元认知以及提升学生对数学方法的价值与审美判断能力．

探究式；解题课；元认知；数学素养

1 问题提出

中学课堂通常分“概念课”“原理课”“解题课”3种课型，“复习课”可以归类到“解题课”．解题课是中学数学教学中非常重要的课型，也是教师们十分重视的教学环节．很多教师甚至把解题课比概念课、原理课看得更重，付出的精力更多．然而目前解题课普遍存在的问题是：课堂上反复刷题，提高学生解题的熟练度，缺少提升学生思维能力的考量．从高考的考题情况分析，除了最后的压轴题，大多数题更多地依赖于考生的解题熟练度．刷题越多，遇到类似题型的几率就越大，得分率也就越高．考试是根指挥棒，有什么样的考试，就会有什么样的教育方式，因此，改善基础教育现状的着眼点或许是考试方式．然而，涉及千万学子的考试改革不是一件一蹴而就的事情，需要逐步进行．考试是检验教育效果的一种方式，并非目的，从教育的角度看，教学不能沦为考试的奴隶，考试与教学的关系不应该本末倒置．但考试作为一种重要的选拔方式，在很大程度上决定了考生们的未来，教学不顾及考试的效果是不现实的．这就存在一个数学素养的提升与应试之间如何平衡的问题．解题课在这个平衡中无疑充当了至关重要的角色，把握得好，可以二者兼顾；把握不好，可能二者皆失．研究者从一则普通的几何题出发，层层拓展，分析在解题课教学中如何引导学生抛开惯性思维，不是基于经验，而是从问题自身的条件出发寻找解决问题的思路，并从中发现有规律性的现象，从而达到举一反三的效果．

2 解题课在数学教育中的作用

哈尔莫斯说：“学习数学的唯一方法是做数学．”[1]适度地解题是数学学习必不可少的环节，但教师应该选择具有启发性的好题，通过这类问题能够让学生发现其中所蕴含的规律，起到触类旁通的效果．

解题课的功能是什么？这是需要首先搞清楚的问题．解题课的功能是在概念课、原理课基础上固化已学的概念、原理、思想与方法，并能熟练运用它们解决问题．其基本特征即探究式或研究式解题，关于探究式教学模式有一个相对传统的解释：“探究性教学模式不仅可以较深入地达到对知识技能的理解与掌握，更有利于创新思维与创新能力的形成与发展，即有利于创新人才的培养．在此过程中，能否取得成就的关键是，学生在学习过程中的主体地位是否能得到比较充分的体现，同时还需要有教师方面的引导、帮助与支持．换句话说，探究性教学模式的成功实施涉及两个方面——既要充分体现学生在学习过程中的主体地位，又要重视发挥教师在教学过程中的主导作用．离开其中的任何一方，探究性学习都不可能有良好效果．可见，‘主导—主体相结合’是这种教学模式的基本特征．”上述定义稍显笼统，并未解释清楚什么叫“探究”．

探究式解题是指教师针对给定的问题从条件出发，创设一系列引导式问题，形成一个层层递进的问题链，引导学生寻找解决问题的思路，其理论基础是弗赖登塔尔的“数学教育是数学的再创造”．众所周知，数学并非是一门演绎科学，当人们试图解决一个数学问题时，并非仅仅是罗列一些条件，然后进行推理．实际上，解决问题是一个不断摸索、试错、猜想、检验的过程．解题课不仅为了固化已学的概念、原理，同时也是培养学生解决数学问题正确方法的重要环节．与数学家研究过程不同的是，学生的认知能力与知识积累有限，不可能像数学家那样完全独立地研究数学问题．事实上，数学教育是在教师引导下学生的“有限再创造”过程．换言之，教师需要通过一系列引导式问题启发学生寻找解决问题的思路．然而，实际的解题课常常是通过重复训练达到一定的解题熟练度，从而提高应试效率．实践表明，重复训练可以有效增加学生的解题经验与熟练度，凭借经验解决相对比较熟悉的题型，从而提高解题速度，它对于应付选拔式考试具有一定的效果．

无论出于提升分析问题解决问题的目的还是应试的目的，两者并无根本矛盾，考试的初衷也是为了检验考生掌握概念、原理、思想与方法的程度，检验学生的数学素养与运用数学理论与方法解决问题的能力．所以，一方面，作为指挥棒的选拔式考试需要改革，使之能真正促进素质教育与考生数学能力的提升；另一方面，课堂教学要兼顾素养与应试两个方面．概念课与原理课两个教学环节不能弱化，关于该问题，已经有一些论著论及（见文[2-7]）．但关于解题课如何兼顾素养与解题能力的提升，相关的研究并不多见．很多关于解题课的讨论都是基于如何解题的，纠缠于解题技巧与细节者较多，缺少解题课对学生思维能力提升方面的剖析．研究者认为，探究式解题课至少应该在教师引导下完成3个方面的教学环节：（1）如何从问题的条件出发通过特例、试错等方法猜测一般规律？（2）如何在前述基础上找到解决问题的方法并反思是如何想到这个方法的？（3）什么是好的方法？第一个环节属于方法的探究过程，第二个环节本质上属于元认知问题，第三个环节则涉及对数学方法的价值与审美判断．

当然，在探究式解题基础上进行适度的解题训练也是需要的，尤其是引导学生通过解题训练进而学会题型与方法分类，对于增加解题经验、提高解题速度无疑是有帮助的，但这已超出本论题的范围．

3 一道平面几何题的思考

平面几何是初中数学的重要组成部分，传统的平面几何逻辑性与系统性都比较强．新课标下的平面几何在此方面有所弱化，更注重与代数之间的联系，生活化的味道也相对浓了一些．几何是培养学生的直观思维与逻辑推理能力的重要载体，如何通过几何问题提升学生的思辨能力值得探讨．

下面这道题的难度中等偏下，有解题经验的学生并不难找到它的解答：“正方形内一点与4个中点依次连接，得到4个区域，其部分区域面积如图1所示，求剩余区域面积．”

这道题蕴含着一个非常有趣的一般规律，如何发现这样的规律则是件有难度的事情．

该题如果出现在解题课上，学生由于清楚了多边形的面积以及计算多边形面积的一般方法，那就是化多边形为三角形或特殊的多边形（例如矩形、平行四边形、梯形等），所以，学生很容易想到的一种方法就是把上述图形分解成若干三角形：

点在正方形内部时，相对的两个区域面积之和相等，即Ⅰ+Ⅲ=Ⅱ+Ⅳ，连接4个顶点，如图2，每块区域利用中点平均分成2块，共8块，重新组合成4块大区域，即：

对比可知：?+20=32+16，

故 ?=32+16-20=28 cm2．

由于已经有了前期的经验积累，因此，学生想到上述方法并不奇怪．

图1 正方形区域面积

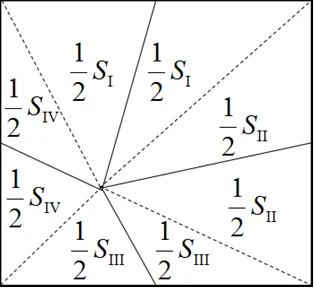
图2 正方形分割

还有一种分割方法也不难想到，那就是连接正方形4条边的中点（如图3），也可完成对4个多边形的三角剖分．

从图形结构来看，4块区域都有一部分面积相等的小区域，同时去掉后，还是一个小正方形，在新的正方形中探究这些小区域的面积关系（如图3）．记4个新区域面积分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ，则有：

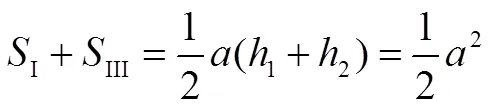
所以Ⅰ+Ⅲ=Ⅱ+Ⅳ，同时增加4个全等等腰直角三角形后，上述规律保持不变，故?=32+16-20=28 cm2．

看起来上述问题似乎已经得到解决，但有一种情况可能会出现，大正方形内的点有可能不在小正方形内部（如图4）：设内点为，当在小正方形外（同时在大正方形内）时，区域的划分会显得复杂．为方便起见，记Ⅰ=△PEF，Ⅱ=△PFG，Ⅲ=△PGH，Ⅳ=△PEH,同理可推得Ⅰ+Ⅲ=Ⅱ-Ⅳ．这说明若点不在小正方形内部,需将两个面积相减．

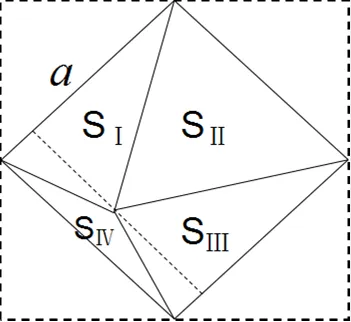
图3 多边形的三角剖分

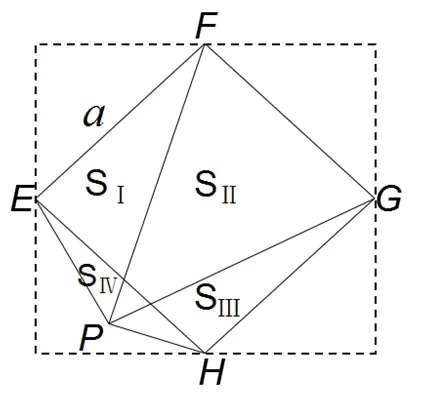
图4 正方形内的动点

上述两个方法的思路是类似的，出发点都是试图将四边形分割成三角形，利用“三角形等底等高则面积相等”这一性质完成问题的解答．但显然第一个方法比第二个方法更简洁，避开了可能出现的分类讨论．所以从方法上评判，第一个方法比第二个方法更优．

然而，以上方法都是基于经验，经过了训练的学生都不难发现这类解题思路，但它们是不是好的方法？什么叫好的方法？通常有几个判断标准：简洁，抓住了问题的本质，方法具有一般性．

上述问题的本质是什么？如果把问题稍微变换一下，类似的结论是否还成立？类似的方法是否还适用？例如，若是把正方形换成矩形呢？或者把正方形边界的中点换成更一般的点呢？此时的问题没有发生本质的变化，上述两个方法依然是适用的．如果将正方形换成圆（到了高中甚至可以换成椭圆）呢？类似的结论是否还成立？这就涉及问题的本质与方法的一般性讨论了．一旦边界是“弯曲的”，第一种方法显然就不能照搬了，因为用此方法无法将4个小区域分割成三角形．第二种方法或许可行，将圆周上的4个等分点连接之后，得到了4个面积相等的曲边区域，割掉这4个小区域后得到一个正方形，问题回到了正方形的情形．从这个角度看，第二个方法比第一个方法更具有一般性．换言之，第一个方法更具简洁性，第二个方法更具一般性．所以两种方法各有千秋，优劣在伯仲之间．

还有其它方法吗？这就需要暂时摆脱化多边形为三角形的惯性思维，以对问题本质的探索作为出发点寻找新的方法．

数学研究的一个基本特征是从特殊到一般．姑且不管是何种区域，问题的关键是区域内一点与区域的4个边界点连接得到4个不同的子区域，这4个子区域之间的关系与内部点的位置是否有关？不妨先从特殊的点出发考察一下这些子区域之间的关系．例如，若内部的点是正方形的中心或者在正方形的一条中线上，结果如何？此时将会发现一个共同的规律：相对的两个区域面积之和相等．再考察更一般情形，中线上的点发生了偏移，变成了正方形内的任意一点，类似的现象是不是还会出现？这样的思考方式有效避开了分割多边形为三角形的惯性思维，虽然最终还是需要利用三角形的面积，但这是探索出来的必然方法，而不是经验的结果，这也是进行科学研究的普适性思维，两者不可同日而语．

不妨先探究一下第三种解答：连接对边中点、，相交于点（如图5），连接、、、、，因为是对称中心，有△POE=△POG，△POF=△POH，同时减去公共部分后有①+②=③+④（数字符号代表区域面积）这说明相对的区域面积总是“相互补充的”（即某块区域面积增加，其对角区域面积会减少相应部分），且对角区域的面积之和为全部面积的一半，对比原图，则必然有?=32+16-20=28 cm2．

上述解法的出发点并非化多边形为三角形，虽然最终还是用到了三角形面积之间的关系，但这种关系建立在探索的基础上而不是经验的基础上．更重要的是，第三种解答抓住的是区域内部点的位置，没有直接去关心边界，这也就使得这种方法具有了普适性．边界是不是直的并不重要，最终需要的并非正方形图形本身，而是正方形的对称性．只要保证交点是整个平面图形的对称中心，即可让“对角区域面积之和为定值”这一性质得以保留，因为中心对称图形的对称中心可以保证原始划分中的对角区域面积之和相等，这可以从平行四边形和椭圆这两种特殊图形中加以检验．

图5 正方形对边中点连线

两种图形均满足SⅠ+SⅢ=SⅡ+SⅣ．

4 解题课课例设计

以上述问题为例，如何在解题课中引发学生去思考从而寻找解决问题的最佳方法，进而提升思维能力？

通过如下一系列问题的设计层层递进，可以引导学生深入思考．

问题1：正方形内一点与4边中点依次连接，得到4个区域，其部分区域面积如图1所示，求剩余区域的面积．

相信无需多少时间，就会有学生给出解答，学生给出的解答很可能是前面的第一种解法．如果学生无法回答，不妨辅以这样的问题：一般的多边形面积如何计算？有了这样的提示后，学生是可以想到化多边形为三角形的．如果学生给出了上述两种不同的解答，则直接进入问题3，否则先考虑下面的问题2．

问题2：这是分割多边形为三角形的唯一方法吗？

学生如果了解了第一种方法，很容易想到另一种分割方法，所以这个问题的回答对于学生应该没有多少难度．

问题3：上述几种方法哪种方法更好？好在哪里？

这个问题的提法可能令学生一头雾水，不知从何回答，不妨问得更具体一点：哪个方法更简洁？哪个方法更具有一般性？

问题4：上述方法的缺陷是什么？除了将多边形分割成三角形，还能想出别的办法吗？

在分析这个问题的过程中应该同时阐明问题的重要性，上述两种方法仅适用于多边形，一旦区域的形状发生变化，这种方法可能就不适用了，但类似的结论是否仍然成立？例如将正方形换成圆怎么办？此时学生或许会想到第二个办法也适用于圆，但如果换成更一般的对称区域呢？通过对这个问题的分析，可以帮助学生了解：分割多边形的方法依赖于区域的形状．它仅适用于正方形或平行四边形，如果边界弯曲，就要想办法把边界割成多边形，所以第二种方法才更具有一般性，但它仍然具有局限性，因为如果是更一般的区域，第二种方法可能也不适用．这两种方法之所以具有局限性，根本原因就在于两种方法都需要转换成多边形才能利用三角形面积完成计算．在此基础上抛出下面更一般的问题．

问题5：假设两条直线交于区域内一点，与区域边界分别交于点、、、（如图7），构成一个平行四边形．线段与将区域分割成4块小区域，使得相对的两块区域面积之和等于整个区域面积的一半．任取区域内一点，与、、、的连线将区域分成4个小的区域，相对的两块区域面积之和是否仍是整个区域面积的一半？为什么？

这个问题中的区域很宽泛，甚至不必要求它是中心对称图形，只要过区域内部一点的任意两条线段被点平分且能将区域分割成4块小区域使得相对两块区域面积之和等于整个区域的一半，那么这4个点就决定了区域内任意点的性质：到4个边界点连线得到的4个小区域相对区域面积之和相等．有了前面的分析基础，学生已经不难应对这个问题．这个结论与区域形状无关，只与分割区域的两条直线的位置有关．在此基础上还可以进一步拓展：

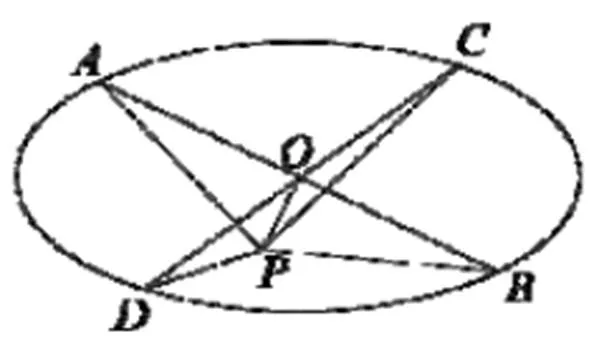
图7 两条直线分割区域

问题6：是不是所有的区域都能找到两条相交直线具有问题5中所说的性质？

这个问题的难度比较大一些，可以作为课外思考题，供有余力且有兴趣的学生思考．其基本的思路是：（1）有没有一条直线将一个给定的区域面积平分？这个问题不难有肯定的回答；（2）过平分区域面积的线段之中点是否存在一条直线将区域分割成具有问题5中所说性质的4块小区域而且交点也是该线段的中点？结论就未必了．不妨把问题5中所说的性质称为区域面积对分性质．

定义1 假设区域的边界上有4个点，内的点到这4个边界点的连线将区域分割成4个相对的区域面积之和相等的小区域，则称为相对于这4个边界点的区域面积对分点．如果区域的边界上存在4个点，使得区域内的任意点相对于这4个边界点都具有面积对分性质，就称该区域具有面积对分性质．

由此可以得到一个一般性的结论，不妨让学生总结成一个定理：

定理1 假设是中心对称的有界凸区域，则具有面积对分性质．

以上一系列问题的分析体现了探索的一般思维方法，思维能力正是在这种探索中慢慢形成的．当然，由于时间所限，所有的解题课都如法炮制显然是不现实的，正如前文所说，需要考虑到素养、能力与应试之间的平衡．定期进行一些类似的探究式解题，学生慢慢就能掌握分析问题过程中的探究方法．

可以作为课外的研究习作，引导有兴趣并有余力的学生围绕着这个问题进一步展开讨论．

问题7：定理1中的中心对称条件是不是必需的？区域的凸性是不是必需的？

中学虽然没有专门介绍凸区域的概念，但此概念并不抽象，学生在理解上并无难度．通过具体的例子很容易发现，如果区域不是凸的，就不能保证区域内任意点到边界点的连线都在区域中，面积对分性质可能不成立，所以区域的凸性是必要条件．那么，中心对称性条件是否可以去掉呢？此时，不妨引导学生先考虑特殊情形，例如，三角形情形如何？凸四边形情形又如何？通过分析会发现，三角形与凸四边形区域都可以通过连接各边的中点得到一个平行四边形（其中三角形为3边的中点加上任意一个顶点）．但到了五边形以上的情形，类似方法就不适用了．问题的焦点集中在能否找到具有类似对称图形中心性质的那种点？利用凸区域边界的连续性可以证明，所有的凸区域都存在一个内接平行四边形，该平行四边形对角线交点就是这样的点．换句话说，该平行四边形的对角线将凸区域分成了4块相对区域面积之和相等的小区域，因而凸区域内的任意点相对于该平行四边形的4个顶点都具有面积对分性质．于是得到一个更一般的结论：

定理2 假设是平面内的有界凸区域，则具有面积对分性质．

5 结束语

概念课、原理课与解题课是数学教学过程中3个不可或缺的基本课型，无论是为了强化对概念、原理的理解与灵活运用，夯实数学基础，提升数学思维能力与数学应用能力还是为了应试，解题课都起着举重轻重的作用．探究式解题对于强化学生对数学概念、原理的理解，提升数学思维能力与解决问题的能力无疑是有帮助的．在现实的大背景下，兼顾学生数学素养的培育与解题的熟练度是解题课需要肩负起的重任．

[1] 哈尔莫斯．怎样做数学研究[EB/OL]．（2019-04-16）[2019-06-12]．https://chuansongme.com/n/2909741451012．

[2] 曹广福．课标与教材浅议[J]．课程·教材·教法，2016，36（4），12-16．

[3] 何勇，曹广福．课堂教学中如何兼顾学生素养与应试能力[J]．数学教育学报，2014，23（2）：63-65．

[4] 张蜀青，曹广福．以问题驱动对数概念课教学[J]．中学数学教学参考，2014（7）：12-13．

[5] 张蜀青，曹广福．以问题驱动的原理课教学[J]．中学数学月刊，2014（8）：34-35．

[6] 张蜀青，曹广福．大学教师与中学教师关于《基本不等式》的“同课异构”评析[J]．数学教育学报，2015，24（6）：40-43．

[7] 曹广福，张蜀青．问题驱动的中学数学课堂教学（理论与实践卷）[M]．北京：清华大学出版社，2018：1．

Inquiry Teaching of Solving Problems by Examples

ZHU Qing-bo1, CAO Guang-fu2

(1. Guangzhou Zhixin High School, Guangdong Guangzhou 510090, China; 2. South China Agricultural University, Guangdong Guangzhou 510642, China)

Problem-solving lesson is an important link to help students solidify knowledge and learn to use mathematical knowledge to solve problems in classroom teaching. Traditional problem-solving lesson pays attention to cultivating students’ proficiency in solving problems and lacks consideration of improving students' thinking ability. The function of problem-solving lesson has two levels, one is educational level, the other is utilitarian level. Through the analysis of a plane geometry problem, this paper discusses how to guide the students to think that what methods can we think of in the face of a problem, and how do we think of this method? What is the best way? Through the inquiry process of methods, students’ meta-cognition is trained and their value and aesthetic judgment ability of mathematical methods are improved.

inquiry; problem solving course; meta-cognitive; mathematical literacy

G622.4

A

1004–9894（2020）02–0049–04

2019–11–06

国家“万人计划”人才项目——问题驱动的中学数学课堂教学

朱清波（1978—），男，中学高级教师，主要从事数学教学与数学教育研究．

朱清波，曹广福．例谈探究式解题课教学[J]．数学教育学报，2020，29（2）：4952．

[责任编校：陈汉君、陈隽]