中国数学教师信念研究二十年

孙丹丹，汪晓勤

中国数学教师信念研究二十年

孙丹丹1，汪晓勤2

（1．华东师范大学 数学科学学院，上海 200241；2．华东师范大学 教师教育学院，上海 200062）

以1998—2018年中国知网收录的数学教师信念研究的论文为基础，从相关论文发表时间、论文作者、关键词、研究主题和研究方法5个维度进行统计分析．研究发现：数学教师信念最近十年来才引起研究者较高重视，已形成两个研究群体，取得系列研究成果，但在后续研究中仍需注意接轨国际研究、夯实理论基础、创新研究方法、拓展研究主题等．数学教师信念的特征、数学教师信念各要素间的互动机制、数学教师信念与实践的关系、数学教师信念与其他心理变量的关系、发展数学教师信念的方式等是值得关注的主题．

数学教师；信念；教师专业发展

1 研究背景

教师信念是国际比较研究TEDS-M（教师教育和发展研究——数学）中数学教师专业素养的两大核心成分之一[1]，原联合国国际教育发展委员会的负责人Combs提出，使教师成为优秀教师的，不是他们的知识或方法，而是教师对学生、自己、他们的目的、意图和教学任务所持有的信念[2]．在中国教育改革的背景下，数学教师信念显得尤为重要，因为新的教育理念必须经由教师信念这一中介变量才能真正转化为课堂中的生产力，Fullan也提出只有教师的信念发生变化，才能有真正的教育变革[3]．从20世纪80年代起，国际数学教育研究者开始关注教师的数学和数学教与学的信念，以及它们之间的关系[4]，取得了较为丰硕的研究成果，中国数学教师信念的研究约起始于20世纪末21世纪初，尤其近十年来，数学教师信念的研究成果增长较为迅速．这里尝试对这些研究成果进行系统梳理，了解当前数学教师信念研究现状，展望未来研究方向，以期为该领域进一步的理论研究和实践探索提供参考．

2 研究设计

2.1 数据来源

在“中国知网”高级检索模式下，第一次以“数学教师”并含“信念”为检索词在主题范围检索，将文献类别限定为数学和社会科学，数据库及检索时间均不做限定，共检索到文献197篇，进一步筛选得到契合数学教师信念研究主题的文献共计75篇，其中，会议论文5篇，期刊论文35篇，学位论文35篇．第二次以“数学观”“数学教学观”或“数学学习观”为检索词在篇名范围检索，进一步以“教师”为检索词在上一步检索结果中再次检索，得到文献41篇，筛选得到契合数学教师信念研究主题的文献共计32篇，其中期刊论文23篇，学位论文9篇，对数学教师信念研究论文发表时间、论文作者及关键词的统计分析针对以上107篇文献展开．

鉴于一般教师信念的研究可能会对数学教师信念研究主题及研究方法有借鉴作用，因此在分析数学教师信念研究主题及研究方法时，研究还参考了部分一般教师信念高被引研究论文，除此之外，还参考了喻平2016年出版的专著《教学认识信念研究》．

2.2 研究方法

总体采取量化与质性结合的混合研究法，具体而言，对数学教师信念研究论文发表时间、论文作者及关键词的统计分析采取量化方法，主要以CiteSpace为分析工具；对于数学教师信念研究主题及研究方法的分析则主要采用质性文本主题分析法[5]，力求通过两种方法的结合，全面而深入地展现1998—2018年间中国数学教师信念研究的现状．

3 研究结果分析

3.1 基于数学教师信念研究论文发表时间的统计分析

将数学教师信念研究论文按发表时间进行排序，绘制成图1．从图1可以看出，研究者对教师外显的行为或具体的知识关注较早，后来才逐步关注到教师内隐的信念．国内数学教师信念研究约兴起于1998年，第一个十年发展较为缓慢，文献总量为19篇，约占比18%，第二个十年发展迅速，文献总量为88篇，占比约82%，这说明数学教师信念的研究起步较晚，自2008年才开始得到较普遍的重视．总体而言，数学教师信念研究的发展是稳步增长的，但局部增长是曲折的，2009年和2014年发文量最大，分别达到12篇和13篇．

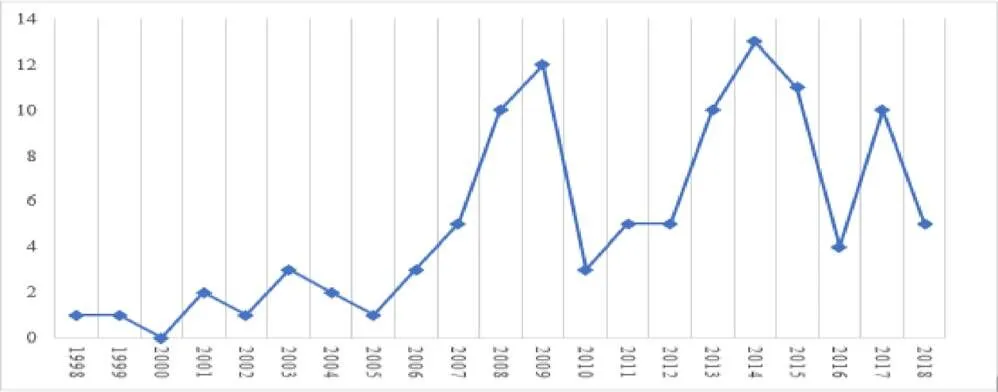
图1 数学教师信念研究论文发表时间分布

3.2 基于数学教师信念研究论文作者的统计分析

将数学教师信念研究论文作者作为分析对象，作者排名不分先后，学位论文作者将导师包括在内，借助CiteSpace对结果的可视化，得到图2．图2中作者姓名的大小与发文频次成正比，作者姓名之间的连线代表作者之间的合作，查看作者及发文数量频次表，将频数超过3次的作者姓名整理成表1．借助图2和表1，可以得到数学教师信念的主要研究者有南京师范大学的喻平、东北师范大学的马云鹏和韩继伟、香港中文大学的黄毅英和林智中、辽宁师范大学的金美月、漳州师范学院的周仕荣等．从作者合作分析可视化图中还可以发现两个合作较为紧密的较大研究群体：以东北师范大学马云鹏、韩继伟和香港中文大学的黄毅英、林智中等为中心研究群和以南京师范大学喻平为中心研究群．除此之外，群体发文量超过3篇的研究群还有以周仕荣为代表的4人研究群．群体成员在核心成员的带动下，更可能围绕一个主题形成较为系统而深入的研究成果．在数学教师信念研究领域，东北师范大学和香港中文大学及南京师范大学的两个研究群无疑发挥着非常重要的作用．

图2 数学教师信念研究的作者合作图谱

表1 数学教师信念研究核心作者统计

3.3 基于数学教师信念研究论文关键词的统计分析

将数学教师信念研究论文关键词作为分析对象，借助CiteSpace对结果的可视化得到图3所示的数学教师信念研究关键词共现图谱．从图3可以看出当前此领域研究的主要关注点．其中，关键词大小与其出现的频次成正比，两个关键词之间的连线代表它们是一篇文献的共同关键词．越靠近中心，关键词越大，说明该关键词越处于核心位置．查看关键词与频数对应表，将频数较高的部分关键词及其频数整理如表2所示．

图3 数学教师信念研究关键词共现图谱

表2 数学教师信念研究核心关键词统计

在排名靠前的关键词中，包含了这样一类：信念、认识信念、教师信念、数学观、数学信念、数学认识信念、教学信念、数学教学信念、数学教学观、数学学习信念、数学学习观，这在一定程度上反映了数学信念、数学教学信念和数学学习信念是数学教师信念领域的重要研究主题．同时，由于观念与信念的混用，数学观、数学教学观、数学学习观就成了一套与信念基本平行的话语系统．除此之外，由于信念与认识信念的关联，数学认识信念、教学认识信念也是常出现的关键词，它们彼此间的联系和区别，会在后文进行阐述．

还有一类排名比较靠前的关键词：数学教师、中学数学教师、职前教师、师范生，反映了数学教师信念领域的两类主要研究对象是在职教师及职前师范生．“教学行为”出现频次很高，说明信念与行为的关系可能是各研究考虑较多的一对关系．

3.4 基于数学教师信念研究论文研究主题的分析

3.4.1 数学教师信念的内涵

要回答数学教师信念是什么，研究者一般会从信念的定义入手．目前，关于信念的定义仍然不统一，而且信念常常容易与观念、信仰甚至知识混淆在一起，有研究对此做了区分[2，6]．一般而言，信念指人们心理上所持有的相信是真实的理解、前提或主张[7]．数学教师信念是数学教师持有的信念，一般特指与数学、数学的教与学等有关的思想和观点[4]．

认识信念包含于信念之中，即认识信念是信念的子集，它特指个体对知识的基本特征以及知识获得过程的基本特征所作的主观判断[8]．喻平认为，如果把问题框定在教育领域，对知识本质的认识以及对知识获取的本质的认识，既与学生有关也与教师有关，因此教师教学认识信念指教师对知识本质特征、对学生获得知识过程基本特征、对教学本质与过程等3方面的认识所形成的一个相对稳定的、带有一定意动成分的基本观点、态度和心理倾向[8]．

由于信念与认识信念的区别，数学教师信念与数学教师认识信念原有着不同的内涵，但在国内研究文献中，当具体到数学教师时，信念的含义窄化，认识信念的含义泛化，结果是两者的含义已经非常接近，均主要指数学教师对数学、数学教与学的认识．

3.4.2 数学教师信念的外延

要想对数学教师信念进行研究，除了要阐明什么是数学教师信念，也即概念内涵，还要界定或阐述数学教师信念包括什么，也即概念外延．概念内涵通常是说法不一的，所以，采取较为公认的内涵说法，去诠释概念外延不失是一种解释概念的途径．具体到数学教师信念，即讨论数学教师信念的构成要素．

数学教师信念通常分为3部分：数学信念、数学教学信念、数学学习信念[4，7]．数学信念指教师对数学的看法，具体表现在对数学学科的看法[7]；数学教学信念指教师对数学教学的看法，即数学该怎么教[7]，包括教师对教学目标、教学过程中教师的角色、学生的角色、适合的课堂活动、教学方法、教学重点、教学步骤、教学结果的认识和看法[9]；数学学习信念指教师对数学学习的看法，即数学该怎么学[7]，包括教师对数学学习过程、学生的行为、学生的心理活动、组成学习活动的成分的看法[9]．

除了以上3部分，康武提出数学教师信念结构中还包括教师的教学效能感，教师的教学效能感又包括两方面：个人教学效能感和一般教学效能感[10]．Calderhead把教师信念归纳为5个相互关联的领域，其中之一是教师关于自我和教师角色的信念，即教师的教学效能感．杨豫晖也把数学教学效能感作为教师教学信念的一部分[11]．

喻平提出了两种数学教师教学认识信念的结构．一种是五因素结构．即数学教师教学认识信念包括教师对数学知识的认识信念、对数学学习的认识信念、对数学教学的认识信念、对学生的认识信念、对自我的认识信念．另一种是二因素结构，即数学教师教学认识信念分为数学知识信念和数学教学信念，其中每个因素都具体包含若干子因素[8]．数学教师对学生的认识信念，具体包括数学教师对学生智力因素和非智力因素发展的认识信念、教师对学生个体差异的认识信念等，开始作为一个相对独立的因素得到研究者重视．

教材观作为课程观的一部分，也被有些研究者纳入数学教师信念系统，有的与教学信念等信念并列[6]，有的隶属数学教学信念[8]．除此之外，诸如数学史信念、信息技术信念或针对某具体的数学分支的信念，如教师对平面几何的教学信念等一些其他类型的信念也开始得到研究者重视[12-14]．

数学教师信念系统中包含各种不同信念，这些信念之间具有怎样的关系，金美月等总结了3种不同观点：教师的数学信念决定其学习信念和教学信念，教师数学信念和数学学习信念与教学信念之间相互作用，教师的数学信念和数学学习信念与教学信念之间不存在必然联系[4]．后有实证研究提出教师的学科信念是信念系统中的关键要素[15]，金爱冬基于对课改前后数学教师信念的调查，也认为数学教师对数学学科的信念是最中心的信念，这种认识很难改变[16]．

综上可知，无论是“信念—数学教师信念”的发展路径，还是“认识信念—教学认识信念—数学教师教学认识信念”的发展路径，最终数学教师信念都包含5个主要构成要素：数学知识、数学教学、数学学习、教师、学生，此时数学教师教学认识信念与数学教师信念各组成要素内涵似乎也已无显著区别，但两者对要素倾向性分析方式存在差异．关于数学教师信念的研究，有些只关注其中的一部分，有些则囊括5部分，甚至更多，大多数数学教师信念研究都关注数学知识、数学教学、数学学习信念．

3.4.3 数学教师信念的倾向性

倾向性是人们对一个事物的看法和认定[8]．数学教师信念倾向性的分析有不同的分析单位，可以直接将数学教师信念作为一个整体，分析其不同的倾向性，也可以先把数学教师信念分解为几个构成要素，然后分析每个要素的倾向性．

Smith宏观地将教师信念分为发展取向和传统取向的两类：发展取向的教师秉承自由、开放、儿童本位、发展导向的观点；传统取向的教师秉承限制、保守、教师本位、规范取向的观点．杨豫晖借鉴此研究，从宏观层面把教师教学信念分为“知识传授为本”和“知识传授与数学思维发展相融合”两种取向[11]．喻平也以传统（绝对主义观念）—现代（相对主义观念）作为教学认识信念的两种倾向，依据教育理论的发展、时间上的差异等界定出所谓的传统和现代[8]．二分法的倾向性划分方式较为笼统，但抓住了各种不同信念的主要矛盾，信念归属类别较容易判断．

下面分别分析数学教师信念主要构成要素的倾向性．

Ernest将数学信念分为3种类型：（1）问题解决观念，认为数学是动态发展的学科，是人类在探索和追求真理的过程中积累起来的，任何数学结果都需要完善和补充；（2）柏拉图主义观念，把数学看作是一个静态不变的学科，数学体系中的各个结构与真理依照逻辑结合起来；（3）工具主义观念，认为数学是为了满足客观世界的需要，由事实、规则、技能组成的一套工具[4]，许多研究采用了Ernest的分析框架．Ernest对数学信念类型的划分是从数学学科出发的，除此之外，也存在数学信念其他倾向划分方式，这些划分方式可视为从一般知识论出发，例如Lerman将数学信念分为绝对主义的观点和谬误主义的观点[4]，喻平在分析二因素结构模型中数学知识信念的倾向时，将知识认识信念分为二元绝对论、多元绝对论、分离性相对绝对论、联系性相对绝对论、相对可误论[8]．

有研究把数学学习信念分为传统和非传统的学习信念，前者认为学习是学生被动地接受新知识，在教学过程中，学生服从教师的安排，学习的目的是掌握一些技能，后者把学习看成主动建构的过程，主张提高学生学数学的兴趣[4]，也有研究把数学学习信念分为行为主义的学习观、信息加工主义的学习观和建构主义的学习观[4]．

Kuhs和Ball指出了4种数学教学信念：（1）以学生为中心；（2）以内容为中心；（3）以练习为中心；（4）以课堂为中心[4]．也有研究提出行为主义和建构主义的二元数学教学信念[3]．喻平在二因素结构模型中将数学教学信念倾向分为行为主义、认知主义、信息加工主义、个人建构主义、社会建构主义[8]．

数学教师信念倾向性通常从数学教师信念或其一级子因素开始划分，二级子因素的倾向性常根据一级子因素倾向性得到．以上只是几种常见的倾向性划分方法，在具体实证研究中，研究者对于倾向性的划分可能不尽相同．为了较好地区分教师不同的信念，数学教师信念倾向的类别数量要适中，类别太少，可能捕捉不到某些特殊的信念类型，类别太多，教师信念的类别从属又可能会难以辨别．无论倾向性类别多还是少，最重要的是要按照一定规律进行划分，且每种倾向的内涵要界定清楚．

3.4.4 数学教师信念的特征

目前国内鲜有数学教师信念研究阐述数学教师信念特征，对于一般教师信念特征已经有了一些论述，但这些论述多起源于国外研究者，由国内研究者引入．例如，林一钢介绍了Rokeach和Green的研究．Rokeach首先提出了“信念系统”一词，他认为一个人会形成对自然界和社会的许多不同的信念，这些信念聚合在一起，便构成了“信念系统”．对于信念系统，他提出3个假设：并非所有信念都同等重要，信念各有不同的重要性，且以“中心—边缘”的形式组织；越接近中心的信念越难转变；越接近中心的信念转变，对整个信念系统其它信念的影响越大．林一钢认同以上说法并提出教师信念本身也是一个系统，处于教师个体信念系统中的某一个层次，边缘的教师信念日积月累的变化能导致中心信念的变化，进而转变整个教师信念系统[6]．Green也提到了信念的“中心—边缘”组织形式，还提到了信念的另外两个特征：（1）近似逻辑性：信念并不是按照逻辑法则的前提和结论组成，而是按照主体的看法来排列的，因此一个人可以同时持有互相矛盾的信念；（2）组合结构：信念以一组组的形式聚合在一起，由于信念具有评价和情感的成分，因此个体会把好的判断与坏的判断分成不同的组别加以组织，信念的这两个特征说明了信念与知识的组织形式可能存在很大差别．在信念的表征方面，林一钢提到有些信念教师能意识到，且能用语言有效表达，有些则相反[6]．

以上这些信念特征是针对一般教师信念而言的，对于数学老师来说，如果其信念满足以上教师信念的特征，那数学教师的中心信念是什么，边缘信念是什么，各种信念是如何进行组合的，这对转变教师信念有哪些启示等都是值得进一步探究的问题．

3.4.5 数学教师信念的影响因素

数学教师信念的影响因素主要可归为以下几类．

（1）个体所经历的教学活动、社会环境．教师教育信念应该看作是个体建构和文化信息相互作用的结果，是社会历史文化的产物[16]．从纵向维度看，个人成长所经历的社会文化背景、教育环境以及人际沟通的场景、家庭的教化，都会对自身的认识信念系统产生影响[17]．数学教师的信念在其学生时代，受个人经验和学校的影响，形成雏形，再经过师范教育，其学习信念和教学信念逐渐稳定．教育实习中指导教师的数学学习信念对他们也有很大的影响[4]．从横向维度看，有两个因素对在职教师认识信念的形成有重要的作用．其一，教师共同体内部交流的作用．其二，整个教育大环境的制约作用[17]．

（2）教学实践结果．教师在课堂中实施某种教学方式后，只有看到（感受到）学生的学习结果发生了改变，才会带来教师信念和态度的转变[7]．Guskey认为教师信念能否改变，很大程度上取决于教师教学实践的结果，教师专业发展致使课堂教学实践的转换，造成学生学习结果的变化，进而引起教师信念和态度的转变[6]．此外，在《信念：数学教育中的潜在变量？》一书中，作者把信念改变与实践改变之间看作是循环的关系，无论从何处开始，它们都是相互影响的[18]．

（3）反思．Vosniadou认为职前教师缺乏元认知的觉醒，他们并不察觉自己信念假设性的本质，而把他们当作“真理”不加批判，Dole研究发现，反思能力是影响职前教师信念转变的两大因素之一[6]，Ernest也指出，教师对自己信念的认识层次和对教学的思考程度极大地影响数学教师信念体系[4]，上述各位学者都强调批判反思能力对教师信念转变的作用．

（4）替代性经验．基于西方教师信念研究，吴壁如提出除了亲身精熟经验，替代性经验也是教师建构和转化自己信念的途径之一[19]．如此，他人的实践结果和他人的反思报告都有可能对教师信念的转化产生积极作用．

（5）系统影响．Clarke和Hollingsworth认为教师信念和态度属于教师个体领域，而个体领域与外部领域、实践领域和结果领域会互相影响，这4个领域通过教师的践行与反思联系在一起，形成了影响教师专业发展的复杂系统[6]．该互通模型将外部环境、实践结果等信念影响因素都纳入其中，而且指出践行和反思是连接各个领域的纽带．

对数学教师信念影响因素的分析有助于回答以下两个问题：（1）什么因素导致了目前教师的信念状态；（2）如果要转变目前教师的信念，可以从哪些角度入手．目前，数学教师信念影响因素的研究以理论思辨为主，实证型研究多是对思辨结果的验证，如何基于实证将影响因素的研究推向细致是值得探索的主题．

3.4.6 数学教师信念现状

相当一部分实证类研究的研究问题集中于数学教师信念现状调查．Ernest提出过在教师信念系统中存在着“宣称的信念”和“行动中的信念”的差别[15]．数学教师“宣称的信念”现状目前主要通过两种方式获得．一是大规模的问卷调查，如李美玉研究了50位高中数学教师的信念现状[20]，王晓明研究了101位初中数学教师的信念[21]，孙虎调查了57位数学教育专业就读的职前教师的信念[22]；二是小范围的访谈调查，如金爱冬通过访谈分析7位数学教师数学课程改革前后的信念[16]，黄毅英和林智中通过让教师估计其所列举情境是否属于“做数学”、评论数学家提出的与数学有关的观点来探讨数学教师的数学观[23]．“实践的信念”可以从教师对与行为有关的问题的回答中推测得到．如杨豫晖通过访谈寻找教师的“本土信念”和所关注的焦点教学因素，分析、推断出教师教学行为背后“隐含的信念”[11]；也可以通过观察得到，如程明喜和马云鹏通过课堂和课外观察来了解6位澳门小学数学教师行动中的信念[24]．除此之外，也有研究者同时挖掘数学教师的两种信念并进行比较．如康敬嫄通过课上观察教师的教学行为和课下访谈教师两种方式挖掘8年级两位教师宣称的信念和实践的信念[25]；脱中菲通过半结构访谈调查3位小学数学教师“宣称的信念”，通过课堂观察实录、刺激回忆访谈收集数据，从数学任务的设计与实施、教学策略的选择与运用、学生的数学理解3个视角分析教师“实践的信念”[15]．问卷调查结果多表明数学教师信念倾向于与高中数学新课程理念要求一致[9，20，26]，深入访谈结果多表明数学教师信念倾向于与高中数学新课程理念要求背离[11，24]．教师信念系统中可能包含互相矛盾的信念，且由于信念的信奉程度不同，在具体情境下，教师会遵循不同的信念行动，这或许是对以上现象的解释之一．此外，问卷题目设计使得教师容易回答“官方”答案，从而隐含教师真实持有的信念也可能是原因之一．

在对数学教师信念现状进行调查的同时，有研究将调查对象分为不同类别进行数学教师信念的差异分析．如，喻平调查了362位中学教师的数学教学认识信念，并选择了样本数较大的4省作比较，了解各省中学教师的数学教学认识信念差异[26]，谢圣英对202名中学数学教师认识信念系统的教龄差异进行了研究[27]，李美玉比较了教学水平较高的教师与教学水平一般的教师在信念上的差异[20]，王晓明比较了不同教龄、性别、学校等教师的教师信念的差异[21]，陈婧则比较了在职中学数学教师和准数学教师的数学教学观的现状差异[28]．目前，信念差异比较所涉及的教师群体已比较全面，不同研究的数学教师信念差异比较结果有些相同，有些则不同[21，27]．在进行数学教师信念差异比较时，尤其需要斟酌比较结果是否有意义，为什么选择这样或那样的两个群体，不能为了比较而比较．

此外，有研究者研究了数学教师对某些特定教学方法的信念．如，牛伟强等借助问卷调查了143位来自上海、河南和新疆等地的高中数学教师对数学史融入数学教学的态度和信念[12]，李红梅基于层次分析法建立了数学教师信息技术信念评估指标体系的分析结构模型[13]．还有研究者专门研究数学教师对某些特定数学内容的信念．如，赵颐从学生的信念、数学教学的信念、数学的社会文化价值等几个维度调查了不同学段的数学教师对平面几何的教学信念[14]．这些研究在一定程度上丰富和细化了对数学教师信念的研究．

3.4.7 数学教师信念与行为及其它心理因素的关系

信念是内隐的，行为是外显的，教师信念与行为之间的关系是许多研究关注的焦点．如，丁福全在调查数学教师的教学信念和教学行为现状的基础上，对数学教师的教学信念与教学行为进行了相关分析、回归分析，还进行了教学信念影响教学行为的路径分析，以探讨中学数学教师的教学信念与教学行为间的关系[29]．杨琳通过观察及访谈开展初中数学教师认识信念对教学行为影响的实证研究[30]．王兴福通过质性与量化相结合的方式，在对中学教师数学认识信念及教学行为现状进行问卷调查和观察、访谈的基础上，研究了中学数学教师数学认识信念对教学行为的影响[31]．结果显示，数学教师信念与行为之间存在显著相关关系[29-31]，但影响中学数学教师课堂教学行为的因素非常复杂，既有内在因素，又有外在因素[31]．数学教师的教学行为与其信念一般具有一致性，但由于个人知识能力或外界因素的限制，教师信念与行为也可能出现差异[29，31-32]．

除了数学教师信念与行为一致性的比较研究外，有研究者更加细致地研究了信念与行为的关系．如，谢圣英研究了中学数学教师的认识信念系统与教学监控能力的相关性，希望以此增强对数学教师观念与教学行为“不一致”现象的解释力，该研究分别分析了中学数学教师认识信念系统和教学监控能力的结构，编制和修订测量教师认识信念系统量表和教学监控能力量表，然后就中学数学教师认识信念系统与教学监控能力各子因素开展了两者关系的全模型研究[33]．喻平分析了信念与行为的中介因素，该研究通过理论分析得到教师的教学行为受到教学认识信念与知识结构的共同影响，并猜想教师的情境性知识可能是一个中介变量，然后通过路径分析验证了教师的理论性知识和教学认识信念通过情境性知识这个中间变量对教学行为产生影响[8]．

无论是教学行为还是教学监控能力，无论是直接影响还是通过中介变量产生影响，以上关系都存在于信念及信念对其有影响的变量之间，有研究探讨了信念及对信念有影响的变量间的关系．如，吕国光借助多种调查数据，探究了教师工作投入程度、教师反思智力、批判思考倾向、工作满意度、教师教学效能感等因素和教师信念之间的关系[34]，蒋奇研究了数学教师的教育信念与数学史素养的相关性，并发现数学史素养对数学教师教育信念有显著影响，数学史素养越高，对数学教育信念的影响越大[35]．

3.4.8 数学教师信念的发展

周仕荣从数学学习经历看师范生教学信念的发展，具体研究职前数学教师经过专业课程、数学教育方法课程和教育实习的学习和训练，教学信念是怎样发展的[36]．还有研究者抓住师范生教育经历的特殊环节，如实习、教学技能比赛等来看职前教师信念的发展．如，臧燕通过访谈及对半年的实习过程中职前教师的教学设计、课堂实施和课后反思进行比较，从而间接对两名职前教师的教学信念有无发生转变做出分析[37]；郭桂容和周仕荣研究了数学系师范生在教育实习中对教师身份的理解的变化[38]；冯振举和王惠扬子通过跟踪分析一位个案教师实习、教学技能比赛、比赛后期又改进的不同版本的勾股定理教学设计，探究职前数学教师教学设计信念的前后变化，试图发现职前教师如何用HPM视角下的数学教学设计信念指导自己的教学设计[39]．以上教师信念的发展变化均是以职前教师为研究对象．金爱冬结合访谈和课堂表现，分析了7位在职教师课改前、课改初、现在3个不同时期信念的变化，通过数学教师课程改革前后的信念表现，把数学教师信念变化类型分为3类：改革保守型、改革激进型、改革不变型[16]．

除了在教师自然教育经历过程中看教师信念发展情况，也有研究以发展教师信念为目标采取教育干涉，分析教师信念变化．如，彭刚以“发展职前教师数学观”为导向开发了“数学发展史”课程，通过丰富职前教师的数学世界，促进职前教师数学观的发展[40]．

3.5 基于数学教师信念研究论文研究方法的分析

3.5.1 量化——量表评估

借助问卷可以对数学教师信念进行大规模调查，从整体上了解教师群体所持有的信念现状．问卷调查需要规范高质量的问卷，在问卷编制方面，已经有研究做得比较规范，在理论综述的基础上形成问卷初稿，然后借助项目分析、信度分析、探索性因素分析、验证性分析等统计手段尽可能保障问卷信度和效度．如，喻平和谢圣英对数学教师教学认识信念测试问卷的编制[41-42]．通过问卷调查得到数据后，借助统计手段进行数据分析也是很关键的，常用数据分析方法有描述教师信念现状的简单描述性统计，比较不同教师信念差异的检验和单因素或多因素方差分析，探究信念与其他变量关系的中介效应分析和结构方程等．

虽然量化分析有其独到的优越性，但要深入揭示数学教师信念体系缓慢变化的过程，以及教师信念体系对教师实践活动的影响程度，量的研究方法也存在局限性[4]．

3.5.2 质性——个案研究或民族志

除了通过问卷作答来了解教师的信念，还有许多其他方式，如何让内隐的信念外显出来是研究中很重要的第一步，甚至有研究提出研究教师信念本身就是创造一系列的方法，来外显、澄清教师信念的过程[6]．数据收集方法包括访谈法（一般访谈、传记式访谈、回溯式访谈）、概念图法、凯利方格技术、日志分析、传记法、隐喻法、出声思维、刺激回忆、文件分析等[3-4]．

以上方法都依赖于教师的个人表达，除此外，研究者的切身观察也是了解教师信念的方式之一，其独特优势在于可以根据教师真实行为表现推测其真实持有的信念，这种信念可能会被教师的问卷作答或访谈言语掩饰．通过观察来了解教师的课堂实践，将教师宣称的信念和实际教学行为来加以比较用以了解隐蔽行动信念的存在[3]．

以上是数学教师信念的质性研究中常用的数据收集方法，这些方法常嵌于更上位的研究方法中，如案例研究、叙事研究、民族志研究等，依靠这些方法的精致设计可以更加深入而细致地剖析教师信念．

3.5.3 多元混合

量化与质性研究各有利弊，具体选用何种方法要依据其与研究问题的匹配程度．就教师信念而言，Kagan认为，运用单一研究方法的研究设计是有问题的，因为教师信念的复杂性不可能用单一的研究方法获悉，她建议设计多元方法进行研究，这样做不仅可以提供研究方法上的三角互证，更主要的是有可能获悉教师信念的复杂性和多面性[6]．康武也提到访谈研究和问卷测量要结合起来，问卷测量可以了解教师信念的大致轮廓和整体情形，访谈研究则能了解教师信念深层的、内隐的部分[10]．实际上，混合研究已出现在目前实证研究中，如王兴福就用了量化与质性两种方式探究数学认识信念对其教学行为的影响[31]．

4 思考与展望

总地来说，数学教师信念的研究近十年来发展迅速，取得了一定进展，但仍处于研究初期，也有很多问题和议题值得关注和进一步研究．

4.1 夯实研究基础

数学教师信念系统的结构要素及倾向性是进行数学教师信念研究的框架，是其它一切研究的基础．只有研究者深刻把握各种倾向性内涵，才可能将教师信念的书面或言语表征抑或行为表现与其相应倾向性建立联系，否则对教师信念的解读就会流于表面．如，要想研究数学教师的数学信念，研究者首先要对数学的本质有深刻地了解，而不能仅从表面借用他人的分类框架．对于质的研究，如果研究者对数学内涵没有深刻把握，会很难解读教师的信念表征，对于量化研究，如果研究者对数学内涵没有深刻把握，问卷指标的设计及解读就会存在很大问题．但是目前专门针对数学教师信念要素及倾向性进行的研究并不多，所以，充分借鉴数学哲学及数学教育哲学的相关研究成果，阐述数学教师信念的构成要素及倾向性内涵，夯实数学教师信念的研究基础，让实证研究有牢固依托，是非常有必要的．

4.2 拓宽研究主题

当前数学教师信念的实证研究主要集中于描述当前数学教师的信念现状，或进行不同类型数学教师信念现状的差异比较．描述现状是数学教师信念研究链上必需的一环，是更进一步研究的基础．与数学教师信念现状及差异研究比较起来，数学教师信念很多其它方面的研究就显得比较薄弱．数学教师信念的组织有何特征，是否如一般教师信念一样有着核心信念和边缘信念？如果是，哪些是居于核心哪些居于边缘？这些信念之间是否会相互作用？相互作用机制又是什么？这些问题需要进一步探索．数学教师信念的重要性被许多研究者肯定，作为从事一切活动的支配力量，数学教师信念与教学实践究竟具有怎样的互动关系？数学教师信念是如何指导其教学实践，教学实践又如何反作用于教师信念也值得研究．有研究提出了信念与实践之间的不一致性，但也有研究提出其它观点：这种不一致是否仅仅由于研究者对教师宣称的信念的真实含义不了解，或者教师宣称的某种信念可能从属于另外一种信念，抑或教师可能无法按照自己真实信念实践[43]，这些说法启发研究者需要深入理解教师对信念意义的建构．

此外，数学教师信念与其它心理变量之间有何关系值得进一步讨论．数学教师信念与教学行为的关系方面已有一些研究成果，信念是直接影响教学行为还是通过其他变量发挥作用？教师信念还与哪些变量有关系？有什么关系？这对了解数学教师信念发挥作用的机制非常重要，但目前这方面的研究少之又少．数学教师信念虽然不易发生变化，但仍然有改变的可能．如何发展数学教师的信念，让广大教师持有更加符合新课程改革需要的信念是需要关注的重要问题，目前此方面的研究几乎没有．关于教师信念发展变化的仅有的研究集中在职前教师教育阶段．即便是针对职前教师，也很少有研究有目的的去发展教师信念，更别说在职教师．如何创设条件改变教师信念，同时基于实证研究找出影响数学教师信念的独特因素，都是当前值得研究的重要议题．

4.3 创新研究方法

目前，数学教师信念的研究方法比较多样．量化研究从问卷设计到数据分析，囊括了检验、方差分析等基础统计方法及验证性因子分析、结构方程等高等统计方法；质性研究包括案例研究、民族志、叙事研究等．具体使用的数据收集方法也比较多样，访谈、观察、本文分析等都有涉及．在后续研究中，研究方法的规范性值得注意，量化分析需要注意研究假设及统计结果的理论意义，案例研究及叙事研究等质性研究方法都需要系统规划．要将访谈、观察等数据收集方法更好地嵌入到整体设计中．除此之外，研究方法的创新性也要引起重视，如何从新的方法论视角思考研究问题，并寻求解决之道，如何使质性研究与量化研究更好地相互借力，服务于研究问题的解决是值得关注的问题[44]．

国际上数学教师信念的研究较早，1989年Ernest和Schoenfeld较为系统地论述了数学教师信念系统框架[45-46]，中国学者对此多有借鉴．此后，国际数学教师信念研究也有长足发展，中国数学教师信念研究要接轨国际，既要引进来也要走出去，踏实做好研究，向世界讲好中国数学教育故事．

[1] 左浩德，裴昌根．数学教师专业素养的概念构建及测评[J]．首都师范大学学报（社会科学版），2017（4）：173-180．

[2] 刘莉，杨艳芳．教师教育信念研究综述[J]．内蒙古师范大学学报（教育科学版），2008，21（12）：45-51．

[3] 林智中，张爽．如何通过质化研究探求教师的信念[J]．全球教育展望，2008，37（8）：52-57．

[4] 金美月，郭艳敏，代枫．数学教师信念研究综述[J]．数学教育学报，2009，18（1）：25-30．

[5] 伍多·库卡茨．质性文本分析：方法、实践与软件使用指南[M]．朱志勇，范晓慧，译．重庆：重庆大学出版社，2017：69-87．

[6] 林一钢．教师信念研究述评[J]．浙江师范大学学报（社会科学版），2008，33（3）：79-84．

[7] 张侨平，黄毅英，林智中．中国内地数学信念研究的综述[J]．数学教育学报，2009，18（6）：16-22．

[8] 喻平．教学认识信念研究[M]．北京：科学出版社，2016：8-9，43，78-83，115-121，186-198．

[9] 金美月，郭艳敏，代枫，等．新课程理念下高中数学教师信念调查研究[J]．现代教育管理，2009，27（4）：95-97．

[10] 康武．信念——数学教师的方向性问题[J]．数学教育学报，2003，12（2）：17-20．

[11] 杨豫晖．教师教学信念的检视与反思——以小学数学教师为例[J]．课程·教材·教法，2010，30（12）：100-105．

[12] 牛伟强，张天群，汪家录．高中数学教师数学史态度和信念调查研究[J]．浙江教育科学，2017（5）：10-12．

[13] 李红梅．基于层次分析法的数学教师信息技术信念评估指标权重的确定[J]．科教导刊（中旬刊），2015，6（2）：53-55．

[14] 赵颐．不同学程的数学教师对平面几何的教学信念调查[J]．贵州师范学院学报，2014，30（3）：51-55．

[15] 脱中菲．小学数学教师信念结构及特征的个案研究[D]．长春：东北师范大学，2014：31，126．

[16] 金爱冬．数学教师信念变化特征及其影响因素研究[D]．长春：东北师范大学，2013：11，122．

[17] 喻平．教师的认识信念系统及其对教学的影响[J]．教师教育研究，2007，19（4）：18-22．

[18] 谢翌．教师信念的形成与变革[J]．比较教育研究，2007，30（6）：31-35．

[19] 吴壁如．教师效能感之理论分析[J]．教师研究资讯，2002，10（2）：45-64．

[20] 李美玉．高中数学教师的教师信念研究[D]．长春：东北师范大学，2013：11．

[21] 王晓明．初中数学教师的教师信念的研究[D]．长春：东北师范大学，2009：9．

[22] 孙虎．数学职前教师教学信念调查研究[D]．上海：上海师范大学，2014：59．

[23] 黄毅英，林智中，黄家鸣，等．中国内地中学教师的数学观[J]．课程·教材·教法，2002，22（1）：68-73．

[24] 程明喜，马云鹏．澳门小学数学教师教学信念的质化研究[J]．数学教育学报，2018，27（2）：41-45．

[25] 康敬嫄．朝汉中学数学教师数学信念问题的个案研究[D]．延吉：延边大学，2017：11．

[26] 喻平．中学教师的数学教学认识信念的调查研究[J]．教师教育学报，2014，1（2）：62-69．

[27] 谢圣英．中学数学教师认识信念系统的教龄差异研究[J]．数学教育学报，2017，26（6）：67-71．

[28] 陈婧．中学数学教师与准数学教师数学教学观的对比研究[D]．长春：东北师范大学，2011：28-36．

[29] 丁福全．中学数学教师教学信念的现状调查研究[D]．桂林：广西师范大学，2008：48-55．

[30] 杨琳．初中数学教师认识信念对教学行为影响的实证研究[D]．南京：南京师范大学，2015：15-29．

[31] 王兴福．中学数学教师数学认识信念对教学行为的影响研究[D]．南京：南京师范大学，2014：134-158．

[32] 张淼．高中数学教师信念及其对教学的影响[D]．长春：东北师范大学，2013：45．

[33] 谢圣英．中学数学教师的认识信念系统和教学监控能力及相关研究[D]．南京：南京师范大学，2013：50-101．

[34] 吕国光．教师信念及其影响因素研究[D]．兰州：西北师范大学，2004：81-116．

[35] 蒋奇．数学教师的教育信念与数学史素养的相关性研究[D]．南京：南京师范大学，2018：34．

[36] 周仕荣．师范生数学教学信念的发展研究[D]．上海：华东师范大学，2007：9．

[37] 臧燕．职前数学教师教学信念转变的研究[D]．济宁：曲阜师范大学，2015：3．

[38] 郭桂容，周仕荣，彭望书，等．数学系师范生在教育实习中对教师身份的理解[J]．数学教育学报，2014，23（5）：91-94．

[39] 冯振举，王惠扬子．职前数学教师教学设计信念转变的个案研究——以HPM视角下的勾股定理教学为例[J]．数学教育学报，2016，25（2）：59-65．

[40] 彭刚．职前教师数学观发展研究——数学史的视角[D]．上海：华东师范大学，2017：5．

[41] 谢圣英．中学数学教师认识信念系统量表的编制与信效度检验[J]．数学教育学报，2014，23（4）：47-54．

[42] 喻平．数学教师认识信念的一个理论框架与量表设计[J]．数学教育学报，2013，22（4）：34-38．

[43] Wilson M, Cooney T J. Mathematics teacher change and development [M] // Leder G C, Pehkonen E, Torner G. Beliefs: A hidden variable in mathematics education. Dordrecht: Kluwer Academic Publishers, 2002: 130-131.

[44] 宋乃庆，周莞婷，陈婷，等．小学数学教师“问题提出”的教学信念研究[J]．数学教育学报，2019，28（4）：24-29．

[45]  Ernest P. The knowledge, beliefs and attitudes of the mathematics teacher: A model [J]. Journal of Education for Teaching, 1989, 15 (1): 13-33.

[46] Schoenfeld A H. Exploration of students’ mathematical beliefs and behavior [J]. Journal for Research in Mathematics Education, 1989, 20 (4): 338-355.

20 Years’ Research on Mathematics Teachers’ Beliefs in China

SUN Dan-dan1, WANG Xiao-qin2

(1. School of Mathematical Science, East China Normal University, Shanghai 200241, China; 2. College of Teacher Education, East China Normal University, Shanghai 200062, China)

Based on the papers collected by CNKI.net on the research of mathematics teachers’ beliefs in China from 1998 to 2018, analysis was conducted from five dimensions of the relevant papers: published time, author, keywords, research topic and research method. It is found that the topic of mathematics teachers’ beliefs has attracted more attention from researchers just in recent ten years. Two research groups have been formed and a series of research results have been obtained, but in the follow-up research, we still need to connect with international studies, strengthen the theoretical foundation, innovate the research methods and expand the research topic. The following topics deserve more attention: the characteristics of mathematics teachers’ belief, the interactive mechanism of elements in mathematics teacher’s belief system, the relationship between the belief of mathematics teachers and their practice and other psychological variables, how to change mathematics teachers’ beliefs etc.

mathematics teacher; belief; teacher professional development

G443

A

1004–9894（2020）02–0076–08

2019–10–10

上海市教育科学研究重大项目——中小学数学教学书的有效设计（D1508）；上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究（A8）

孙丹丹（1991—），女，山东莱芜人，博士生，主要从事数学史与数学教育研究．

孙丹丹，汪晓勤．中国数学教师信念研究二十年[J]．数学教育学报，2020，29（2）：76-83．

[责任编校：陈隽、张楠]