核心素养视角下数学高考试卷评价研究——以2018和2019年江苏高考卷为例

俞梦飞，章 飞

核心素养视角下数学高考试卷评价研究——以2018和2019年江苏高考卷为例

俞梦飞1，2，章 飞1

（1．江苏第二师范学院 课程与教学研究所，江苏 南京 211200；2．南京师范大学 教师教育学院，江苏 南京 210097）

《普通高中数学课程标准（2017年版）》提出了6个数学核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析．分析6个数学核心素养的外在表现形式和相应的水平划分，构建数学核心素养考查的评价框架，并根据评价框架，对2018、2019年江苏数学高考试卷的核心素养考查情况进行比较分析．研究发现，各核心素养以及具体表现的考查分布极不均衡，数学运算（特别是法则运用）、逻辑推理（特别是演绎推理）的考查较多，而部分核心素养和具体表现极少考查甚至从未考查（如问题提出、合情推理等）．建议：从人才培养的高度思考各素养及具体表现的考查比重；加强命题技术研究，力图全面考察学生的学科素养，从而更好地引导教育教学的变革．

数学核心素养；评价；高考

1 问题提出

教育部2014年发布的《关于全面深化课程改革落实立德树人根本任务的意见》中指出：学科核心素养是育人价值的集中体现，是学生通过学科学习而逐步形成的正确价值观念、必备品格和关键能力[1]．2017年版的《普通高中数学课程标准》（以下简称《标准》）中明确指出了数学学科核心素养的概念：数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用的过程中逐步形成和发展的．数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析[2]．高中数学教学自然应注重培养学生的数学核心素养，而高考作为一个终结性评价，具有极强的教学导向作用，同样应全面而准确地评价学生的核心素养．因此，在数学核心素养提出之后，有部分研究者对高考卷中的数学核心素养考查进行了分析．如陈晓、周仕荣[3]比较了2016、2017两年全国3套高考卷中“概率与统计”这一部分的试题对数据分析素养的考查；沈婕、傅剑[4]具体分析了2016年天津卷中各个核心素养各水平考查试题的得分率；李作滨[5]分析了2018年全国卷Ⅰ中6个核心素养试题的考查比例．但以上对于各高考卷中数学核心素养的考查大多仅限于试题的罗列，尚未建立较为完善的评价框架．

为此，这里将细化各核心素养的具体表现以及对应的发展水平，建立数学核心素养考查框架，并具体分析标准颁布之后江苏高考数学试卷（2018年卷与2019年卷）各道试题所考查核心素养的成分、权重、水平等，从而定量化评价高考试卷对数学核心素养的考查状况，进而为高考命题提出建议．

2 数学核心素养考查框架构建

《标准》[2]根据高中学生3种不同层次（即高中毕业水平、高考水平和拓展水平）划分了6个核心素养水平．但一个数学核心素养包含的内容很丰富，仅仅进行水平的划分，不能全面准确地评价学生这一数学核心素养的实际状况．如逻辑推理这一数学核心素养，它包含演绎推理和合情推理两个方面，学生的演绎推理和合情推理的水平可能并不一致．因此，在建立数学核心素养考查框架时，既要关注各核心素养的具体表现，又要考察各具体表现的发展水平．

2.1 素养的具体表现划分

关于各数学核心素养的具体表现，在研读《标准》及其它解读性文献的基础上，以《标准》为重要参考，并兼顾考查的现实可能性，遵循相近归并的原则，与部分专家型教师进行了研讨，基于多次研讨最终对各个核心素养进行了具体表现划分，下面以部分核心素养为例加以说明．如，数学抽象这一核心素养，《标准》指出数学抽象的主要表现为：获得数学概念和规则、提出数学命题和模型、形成数学方法和思路、认识数学结构与体系[2]．“获得数学概念和规则、提出数学命题和模型”表示从现实到数学的形成抽象的过程；“形成数学方法和思路”和“认识数学结构与体系”则表示在形成抽象之后，对于抽象事物（如数学结构等）的认识与理解，也就是理解抽象物；而实际上，数学抽象还表现为对研究对象的一般化思考，对抽象事物的再次抽象等，这些不妨称之为抽象地思考，因此，研究者将数学抽象这一核心素养的具体表现划分为：理解抽象物、形成抽象物和抽象地思考．再如，直观想象这一核心素养，《标准》指出直观想象主要表现为：建立形与数的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物[2]．其中“建立形与数的联系”“利用几何图形描述问题”则是在“形”与“数”之间构建联系并且解决问题，其实质是数形结合；“借助几何直观理解问题”和“运用空间想象认识事物”则是几何直观和空间想象，但是几何直观往往在试题中难以单独出现，因此，将直观想象的具体表现划分为空间想象和数形结合两个方面．再如，数学运算这一核心素养，《标准》指出数学运算主要包括：理解运算对象、掌握运算法则、探究运算思路、选择运算方法、设计运算程序、求得运算结果[2]．其中“理解运算对象”“掌握运算法则”主要是对于算理的理解和掌握，“探究运算思路”“选择运算方法”“求得运算结果”则主要是在算理掌握的基础上，对算法的运用，“设计运算程序”则是设计算法来解决问题，因此将数学运算的具体表现划分为理解算理、运用算法和设计算法．

2.2 素养的水平划分

《标准》是根据情境与问题、知识与技能、思维与表达、交流与反思这4个方面对各核心素养进行水平划分的．首先，对于“情境与问题”方面，《标准》按照“熟悉的情境”“关联的情境”，以及“综合的情境”进行划分，操作性不强；其次，《标准》进行水平划分时默认了这4个方面的水平是一致的，但实际上，具体试题中的“情境与问题”方面可能相对较为简单，是所谓的“熟悉的情境”，但要求的“知识与技能”“思维与表达”等水平可能较高，因此，《标准》中的水平划分有失偏颇．此外，喻平[6]则参照布卢姆模型、PISA模型和SOLO模型将知识学习的水平分为知识理解、知识迁移和知识创新3种水平，喻平的素养水平划分具有较好的操作性，但没有考虑各素养的具体表现．研究者借鉴喻平的素养水平划分的思路，针对核心素养的各个具体表现，尽量从知识理解、知识迁移、知识创新3个层次进行水平划分．例如，数学抽象之理解抽象物这一具体表现，水平一“能理解并用恰当的语言解释给定的数学对象的含义”聚焦知识理解，水平二“能运用已有的学习经验自主研究给定数学对象的性质”关注知识迁移运用，水平三“能将给定的数学对象和已有的数学知识建立联系，形成新的知识体系”则重在创新．当然，水平划分时，还应适当兼顾考查该具体表现的试题的特征，分析影响试题难度的因素，进而确定具体素养的考查水平，力图不同水平间具有明显差异，从而便于对具体试题中考查核心素养水平的标定，凸显可操作性．例如，数学抽象之形成抽象物这一具体表现，从考查实际看，数学对象的原型是影响抽象水平的重要因素，因此，将水平一确定为“能进行实物抽象（即能从多个现实模型中抽象出数学模型）”，水平二确定为“能进行符号抽象（即能从很多个数学模型中抽象出性质等）”，而创新水平则要求“能在已有的数学结论基础上抽象出新的命题、新的概念”，3者层次清晰，便于对试题进行标定，操作性强．为了后文表述的方便，研究者对核心素养的表现以及相应的水平进行了编码，如，将数学抽象中的理解抽象物这一维度记作A1，逻辑推理中的演绎推理中的水平二记作B22，其它素养各维度各水平依此类推．另外，结合高中教学以及考试的要求，并没有要求所有素养的表现水平都分为三级，部分素养的表现水平只进行了两个水平的划分．数学核心素养评价框架见表1．

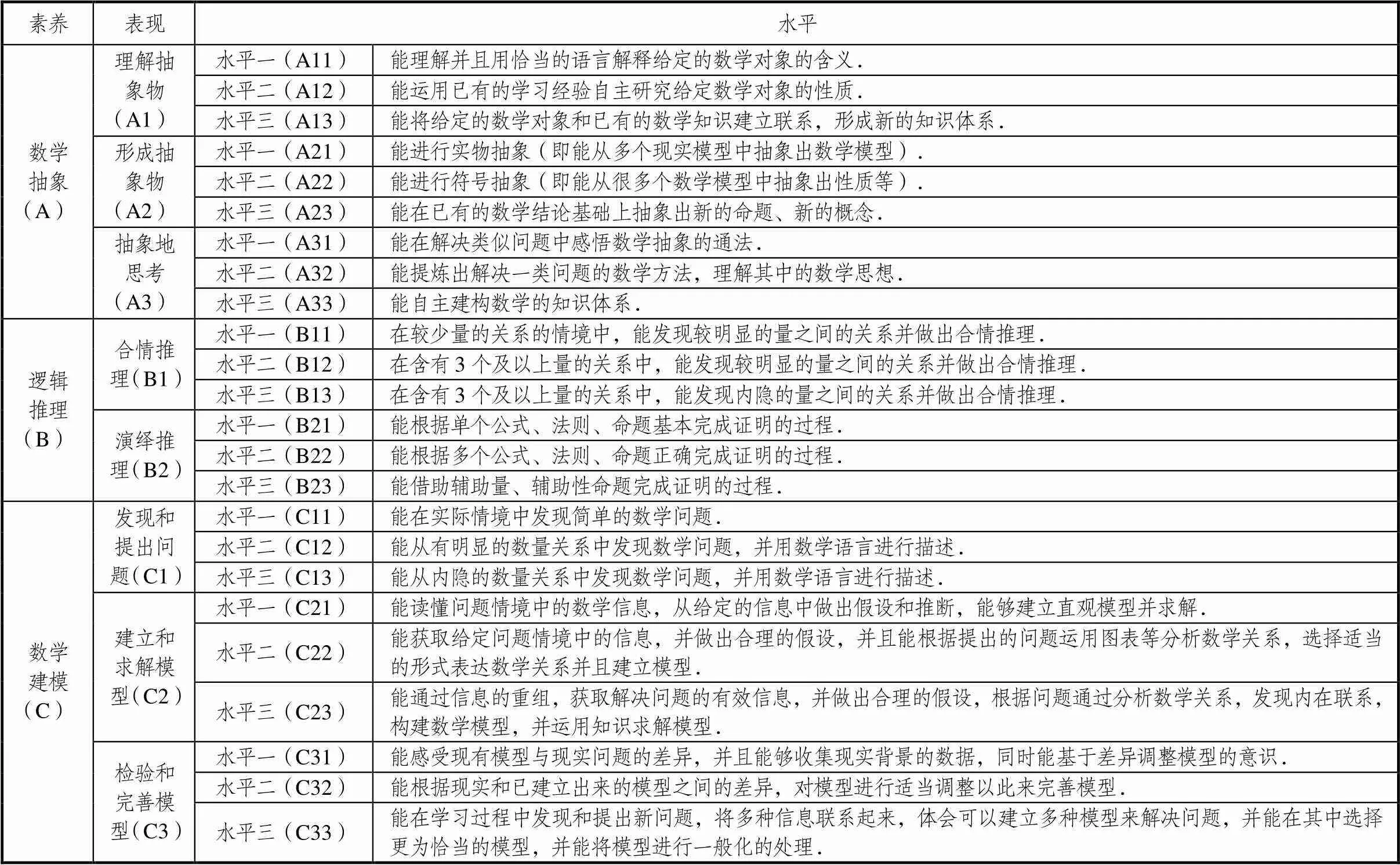
表1 数学核心素养评价框架

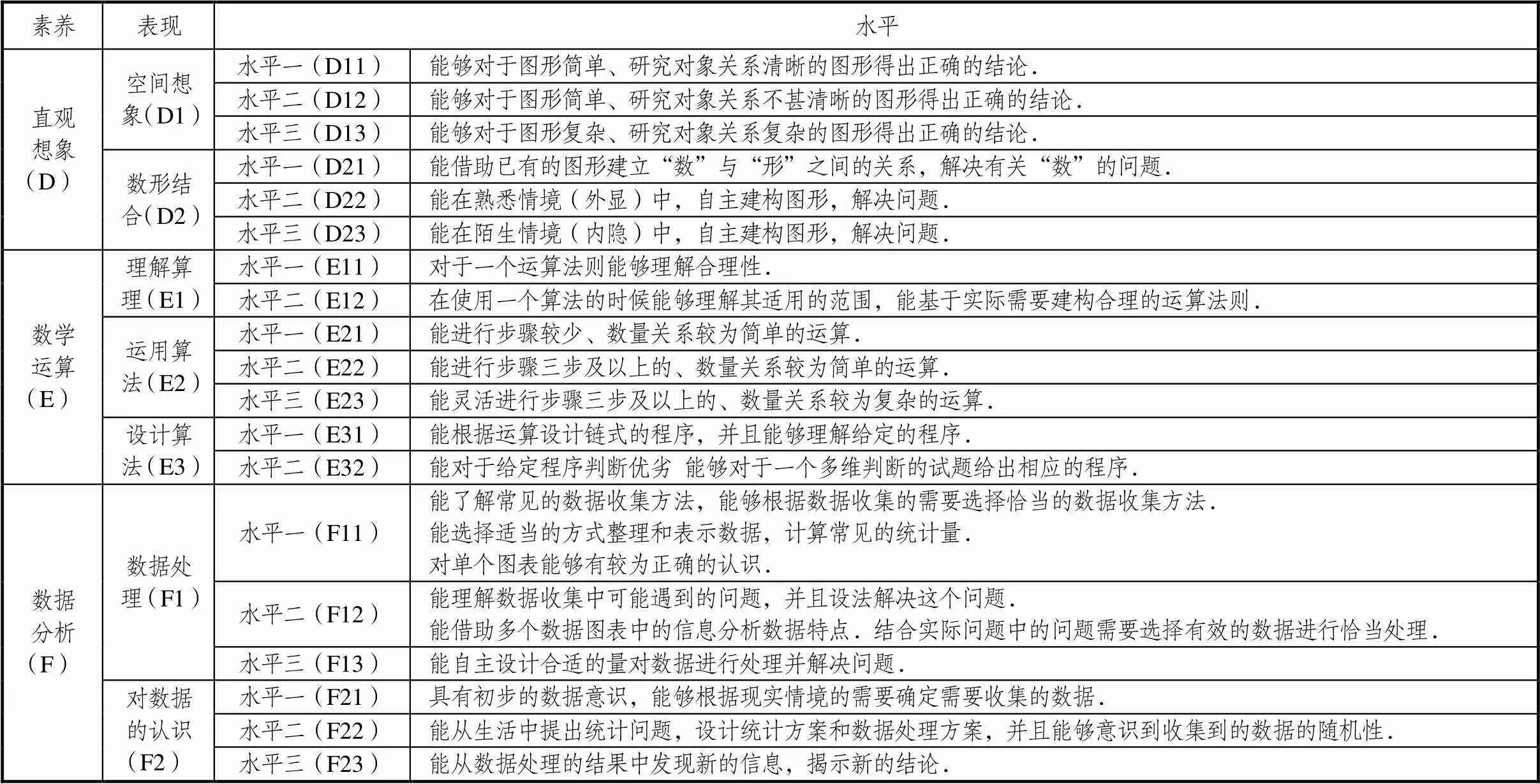
续表1 数学核心素养评价框架

3 高考试题的素养考查现状分析

基于上述评价框架对2018、2019年江苏省数学高考试卷每一道试题进行了分析（如某道大题包含几小问，则每小问分别作为一道小题）．在对试题进行分析时，研究者邀请了5位专家，在详细了解了以上数学核心素养评价框架之后，对各道试题进行分析．在分析过程时，主要遇到了以下几个问题．

（1）对一道试题考查到的素养，有时候不同专家意见不同，此时充分展开讨论，以大家的主流观点确定考查到的

素养．

（2）在确定某道题中各个素养考查的具体分值时，难免也会出现一些分歧，此时，先讨论，然后各自赋值，最后求平均值后再四舍五入，最终确定各个素养考查的分值．

（3）一些试题有两种及以上的解题方法时，先根据不同解法所考查的素养及水平分别赋值，然后商讨各种解法的可能比重，再根据比重加权平均后四舍五入．

3.1 试题素养和水平的确定

例1（2018年江苏卷第5题，5分）

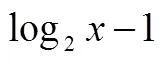
例2（2018年江苏卷第11题，5分）

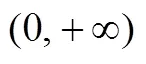
例3（2018年江苏卷第17题，14分）

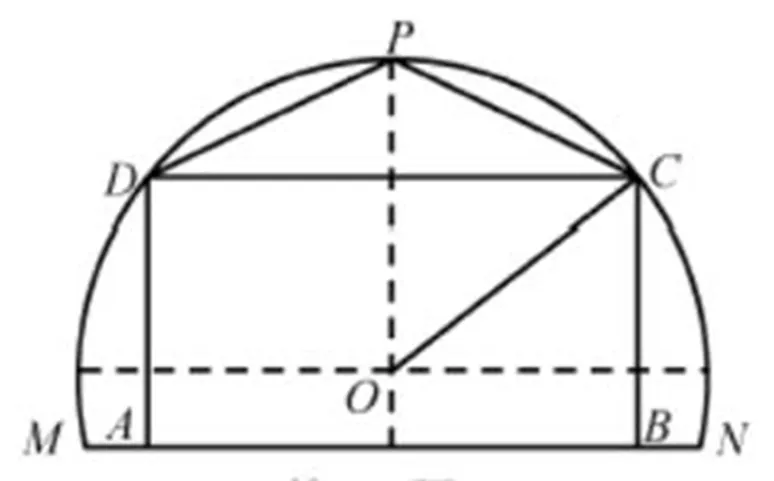
例3有两个小题，分别确定其考查的核心素养及水平．第一小题，要求学生根据图形表示矩形和三角形的面积．首先，需要通过图形得出矩形的长和宽以及三角形的底和高，主要考查的是直观想象中的数形结合，但对数形结合的要求不高，对应水平为水平一．其次，需要根据矩形和三角形的面积公式列出代数式，然后利用三角恒等变换进行化简，考查了数学运算中的运用算法，对应水平为水平二．因此，该小题考查的素养及水平是D21、E21．第二小题，要求学生根据大棚的面积和所种蔬菜的年产值计算两种蔬菜的总产值，需要学生从实际情境中抽象出数学问题，然后根据数学问题建立总产值的模型，最后进行模型的求解，主要考查数学建模中的建立和求解模型和运用算法．对于建立和求解模型的考查，该题可以直接建立模型，考查的水平为水平一，运用算法考查的是水平二．因此，第二小题考查的素养及水平是E22、C21.

3.2 试题各素养水平分值的确定

例1考查的素养较为单一，其素养及水平是E21．该题满分为5分，因此，对E21赋分5分，记为E21–5．

例2考查的素养及水平为B22、E21和D22．该题满分为5分，经讨论，认为其着重考查的是演绎推理，运用算法和数形结合的分量较轻，因此，对B22赋分3分、E21赋分1分、D22赋分1分，记为B22–3、E21–1、D22–1．

例3，第一小题6分，考查的素养及水平为D21、E21，经讨论，认为数形结合考查占比不多，主要是运用算法，因此，对D21赋分2分、E21赋分4分，记为D21–2、E21–4．第二小题8分，考查的素养及水平为E22、C21，着重考查建立模型之后的运算，因此，对C21赋分2分、E22赋分6分，记为C21–2、E22–6．

4 高考试卷的素养考查现状分析

依据上面的框架和方法，对2018、2019年江苏省高考数学试卷中每一道试题进行了素养及水平考查状况的分析，并汇总各年度数据，得到了各年度高考数学试卷核心素养考查的分布及水平状况如下．

4.1 各核心素养考查的分布

2018年江苏高考试卷各核心素养的考查分值依次是，数学抽象8分、逻辑推理47分、数学建模2分、直观想象19分、数学运算81分、数据处理3分．江苏卷满分为160分，各核心素养的考查比重依次是，数学抽象5%、逻辑推理29.3%、数学建模1.2%、直观想象11.9%、数学运算50.6%、数据分析1.9%．2019年江苏高考试卷各核心素养的考查分值依次是，数学抽象4分、逻辑推理53分、数学建模0分、直观想象21分、数学运算80分、数据处理2分．江苏卷满分为160分，各核心素养的考查比重依次是，数学抽象2.5%、逻辑推理33.1%、数学建模0%、直观想象13.1%、数学运算50%、数据分析1.3%．这两年高考卷中各核心素养考查的分布如图1．

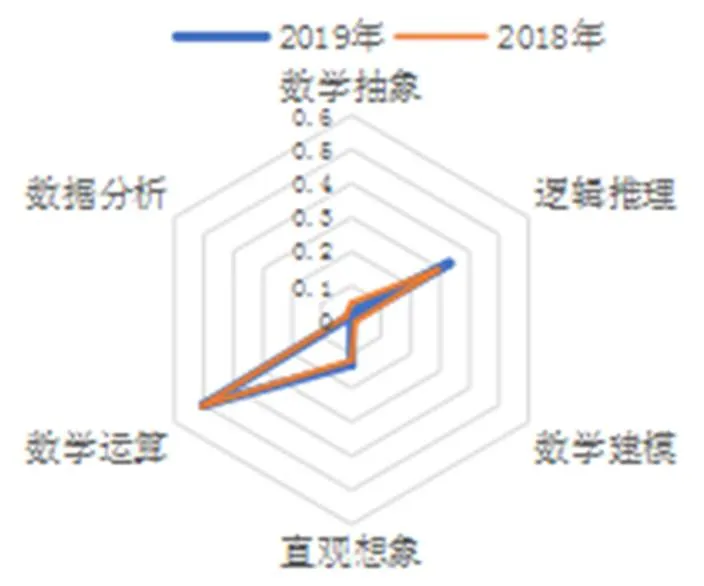
图1 2018及2019年江苏高考数学卷核心素养考查状况分布

可见，江苏数学高考卷核心素养考查的分布极不均衡，主要考查数学运算、逻辑推理和直观想象这3个核心素养（尤其重视对数学运算和逻辑推理两个素养的考查，比重分别约50%、30%），对其余3个核心素养的考查很少，而且2018年和2019年各素养考查比重相近，说明这已成为江苏高考的“常态”．

进一步，对各核心素养具体表现的考查情况进行统计，得到表2和表3．

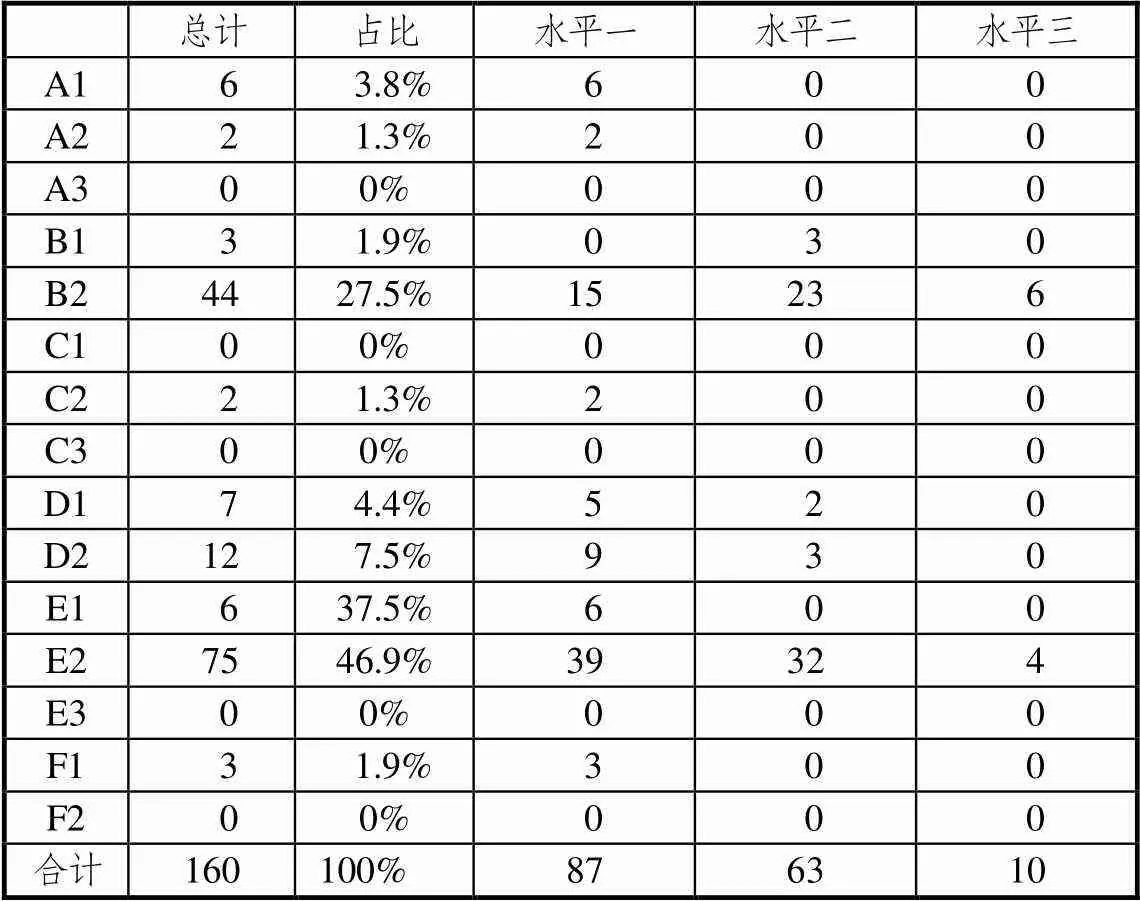
表2 2018年江苏数学高考试卷各核心素养具体表现及 水平分布

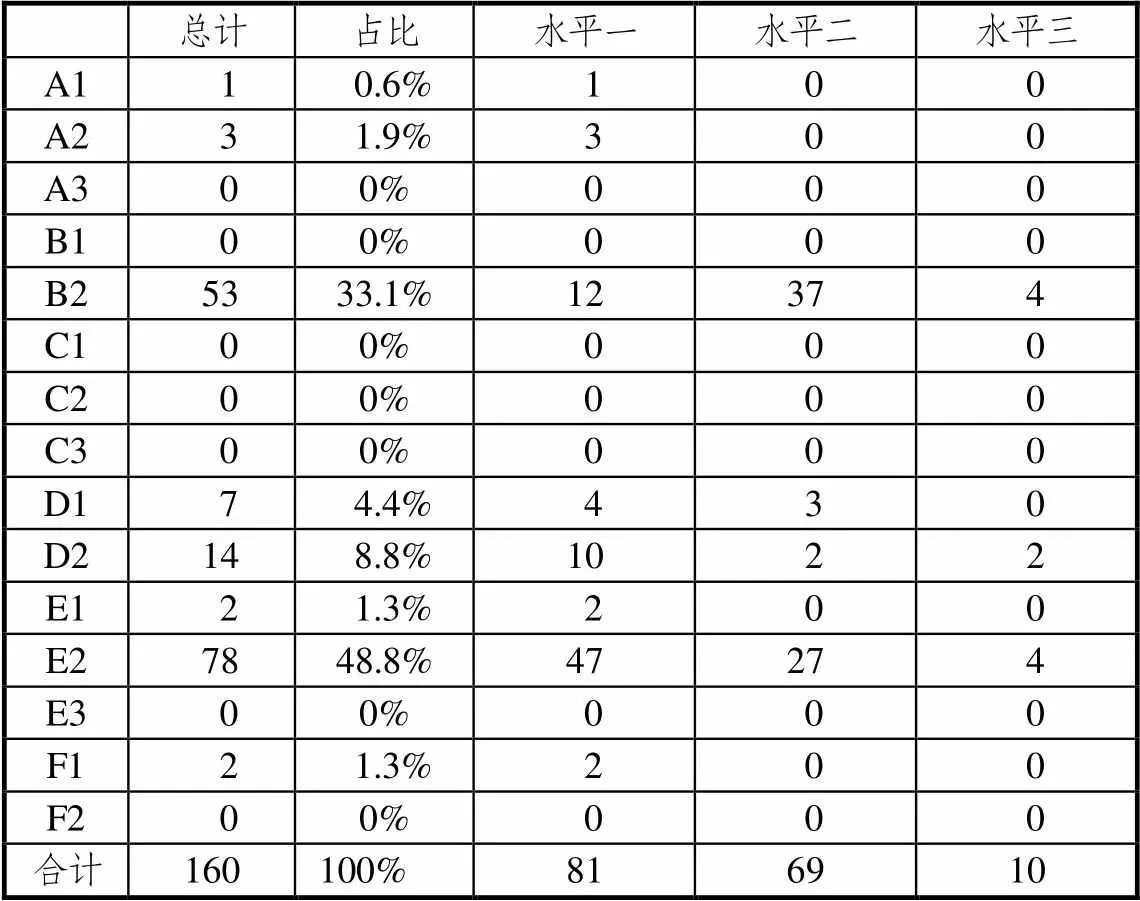
表3 2019年江苏数学高考试卷各核心素养具体表现及 水平分布

可以发现，试卷对同一核心素养各个具体表现的考查也极不平衡，很多具体表现都没有考查（如A3抽象地思考、C1发现和提出问题、C3检验和完善模型、E3设计算法、F2数据认识）．即使考查较多的数学运算、逻辑推理中，具体表现考查分布也不平衡，这两个素养中主要考查的是演绎推理和运用算法，它们在各自素养考查中占比都超过90%．直观想象这一核心素养，主要考查的是数形结合这一具体表现．特别需要说明的是，这两年数学抽象考查的占比较少，但其中2018年考查“理解抽象物”这一具体表现较多，“形成抽象”较少，而2019年则恰好相反．

4.2 各核心素养考查的水平

为了进一步了解核心素养考查水平，分别统计了各个水平占该核心素养的比重，并结合6个核心素养考查的比重，确定了整卷中3个水平的考查比重，两年数据见表4、表5．

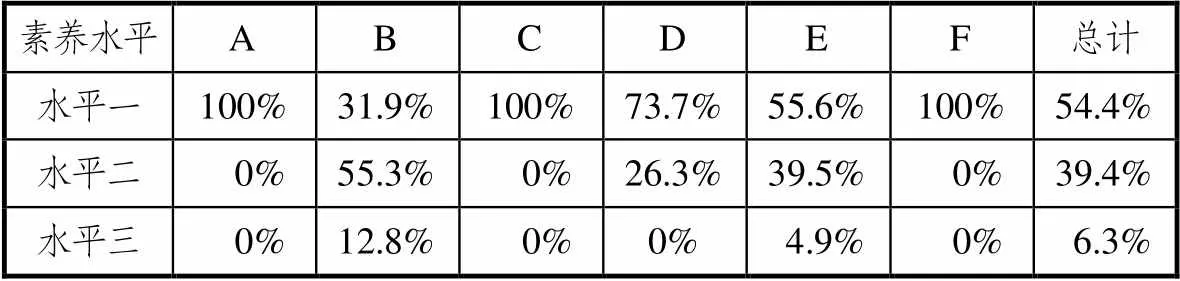
表4 2018年江苏数学高考试卷考查核心素养水平分布

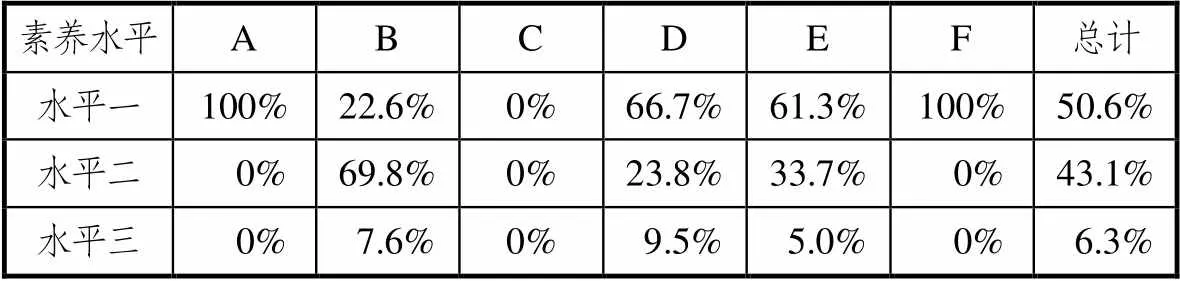
表5 2019年江苏数学高考试卷考查核心素养水平分布

总体而言，2018、2019年对素养水平的考查均为水平一最多，水平二次之，水平三最少，这与高考的要求是相符的．在各个数学核心素养的水平考查上，数学抽象、数学建模和数据分析的考查均为水平一，直观想象和数学运算均是水平一的考查多于水平二的考查，说明在直观想象和数学运算的考查简单的较多，但是逻辑推理的考查是水平二多于水平一，说明江苏高考卷对逻辑推理这一核心素养的要求较高．

比较两年的核心素养考查水平，不难发现2019年高考试卷对于水平一的考查较2018年低，而水平二的考查增加了．具体到各个核心素养，2019年逻辑推理的考查要求较2018年提高了，而数学运算则稍有下降．

5 结论与建议

5.1 结论

通过以上数据，不难得出如下结论．

（1）江苏高考卷对核心素养的考查状况总体稳定．

两年高考卷对核心素养的考查状况总体相近，呈现稳定的态势．可能有两方面的原因：一是，由于高考的性质所决定的，高考毕竟涉及千家万户的利益，涉及社会的稳定，保持高考卷的适度稳定是必需的；二是，江苏已有十余年的自主命题经验，历届命题人相互传承也在一定程度上促进了试卷的稳定．

（2）高考卷中考查的各素养、表现及考查水平存在分布差异．

高考卷对数学核心素养的考查存在较大的分布差异，数学运算、逻辑推理的考查较多；各个核心素养不同，具体表现的考查分布也存在较大差异，一些核心素养的具体表现没有被考查到；各具体表现的考查水平也有差异．差异是自然的．各核心素养及其具体表现都是重要的课程目标，但从课程设计而言，它们本就不是均匀分布的，也无法均匀分布．此外，基于高考这样一个面向全体高中学生的选拔考试，可能部分核心素养的考查还存在一些技术障碍，很难考查．但，在承认素养考查应该存在分布差异的情况下，还需要思考具体素养考查的分布是否合理？

5.2 建议

（1）从人才培养的高度，思考各素养及具体表现的考查比重．

固然各素养及具体表现的考查比重应有差异，但更应思考：这样的分布差异是否符合未来公民培养的要求，是否符合选拔未来高水平建设人才的要求，是否有利于引导教育教学的改革？例如，归纳与演绎是数学推理的两个不同方面，归纳推理在数学发展史以及数学学习中具有十分重要的地位，但高考中归纳推理极少考查，高考直接影响着日常教学的现状下，这自然会对日常教学产生不好的导向，不利于培养学生的归纳推理能力．再如，发现与提出问题，是课程标准提出的发展学生“四能”中十分重要的两个能力，在科技创新日新月异的当下，发现与提出问题的能力，受到世界各国教育界的普遍重视，而高考卷中从未涉及．为此呼吁，本着从未来高端人才培养的需求出发，客观审视各素养及其具体表现，合理确定其考查比重和考查水平，进而引导日常教学．

（2）加强命题技术研究，全面考察学生的学科素养．

一些命题人员常常感叹，很多内容不易考查，如提出问题的能力实难考查．提出问题能力较其它内容难以考查，但是否就不能考查？中国部分地区的中考已多有尝试，为何高考就不能探索呢？可能又有人提出，其阅卷标准难以制定，高考事关重大，万一考虑不周容易引起社会质疑等．实际上，关于问题提出的评价，国际上已有很多相关研究可以借鉴．当然，还有人可能会感叹，提出问题的考查增加阅卷成本，但这点阅卷成本与关乎学生未来发展相比又何足挂齿．总之，一些素养及其具体表现的考查，中国过去没有多少经验，考查也确有一些困难，但这些并非不进行考查的理由，也并非不能考查，只是亟需加强相关素养考查的命题技术研究，希冀通过技术的完善，提升命题水平，全面准确地考查学生核心素养的发展状况，从而更好地引导教育教学的变革，在这方面还有很大的研究与实践空间．相信，但有改革之心，创新之识，有关困难定可迎刃而解．

总之，研究者构建了核心素养的评价框架，框架兼顾了素养表现和水平两个方面，具有较好的操作性，该框架可以迁移运用到不同地区试卷、不同年度试卷以及不同水平试卷的比较研究中．当然，框架的建立、具体试题的评析，毕竟是研究者团队的研讨结果，无法做到绝对客观，还需要基于更多的实践进行框架的适度微调，丰富试题评析经验，提高评析的精准性．基于评价框架，对江苏2018、2019两年的高考题进行了数据分析，对于全国卷相信也有类似结论，为此呼吁加强高考命题研究．权作抛砖引玉，期待同行指正．

[1] 中华人民共和国教育部．教育部关于全面深化课程改革落实立德树人根本任务的意见[J]．师资建设，2014（6）：17–20．

[2] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：1．

[3] 陈晓，周仕荣．从“概率与统计”考点看高考中的“数据分析”学科核心素养——以2016—2017两年高考理科数学全国卷为例[J]．数学通报，2018，57（8）：44–47，62．

[4] 沈婕，傅剑．数学核心素养视角下的考生水平评价分析及教学建议——以2016年高考（天津卷）数学（理工类）试卷为例[J]．考试研究，2017（2）：12–22．

[5] 李作滨．2018年13套高考数学试卷审思：基于核心素养的视角[J]．教育测量与评价，2019（4）：51–57，64．

[6] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19–23，59．

Research on the Evaluation of Mathematics College Entrance Examination Papers from the Perspective of Key Competencies——Taking 2018 and 2019 Jiangsu College Entrance Examination as Examples

YU Meng-fei1, 2, ZHANG Fei1

(1. Curriculum and Teaching Institute, Jiangsu Second Normal University, Jiangsu Nanjing 211200, China; 2. Teacher Education College, Nanjing Normal University, Jiangsu Nanjing 210097, China)

put forward six key competencies of mathematics: mathematical abstraction, logical reasoning, mathematical modeling, intuitive imagination, mathematical operation and data analysis. According to the specific performance and level of these six key competencies, the evaluation framework of key competencies of mathematics was constructed. On the basis of this framework, this paper made a comparative analysis of the core literacy examination of Jiangsu Mathematics College Entrance Examination papers in 2018 and 2019. It was found that the examination distribution of each key competence and specific performance was very uneven, the examination of mathematical operation (especially the application of laws), logical reasoning (especially deductive reasoning) was more, while some core accomplishment and specific performance were rarely or never examined (such as problem posing, reasonable reasoning, etc.). Suggestions: from the perspective of personnel training, we should think about the proportion of each key competence and specific performance; strengthen the research of proposition technology to comprehensively investigate the subject quality of students, so as to better guide the reform of education and teaching.

mathematics key competencies; evaluation; college entrance examination

G424.74

A

1004–9894（2020）02–0035–06

2019–11–18

江苏高校哲学社会科学研究重点项目——“互联网+”背景下师范生教师专业素养发展体系的立体建构与实践研究（2018SJZDI174）

俞梦飞（1996—），女，浙江绍兴人，江苏第二师范学院、南京师范大学合作培养研究生，主要从事数学教育研究．章飞为本文通讯作者．

俞梦飞，章飞．核心素养视角下数学高考试卷评价研究——以2018和2019年江苏高考卷为例[J]．数学教育学报，2020，29（2）：3540．

[责任编校：周学智、张楠]