基于数学核心素养评价框架的试卷测评研究——以2019年高考全国卷为例

李 华，胡典顺

基于数学核心素养评价框架的试卷测评研究——以2019年高考全国卷为例

李 华1，2，胡典顺1

（1．华中师范大学 数学与统计学学院，湖北 武汉 430079；2．西安市长安区第三中学，陕西 西安 710100）

数学核心素养的测评研究是反馈学生核心素养培养成效的重要手段，高考试题是检测学生数学素养的重要载体，因此开展以高考试卷为样本的数学核心素养测评研究对中国新一轮高考改革有重要意义．以2019年全国卷为样本，基于喻平提出的数学核心素养评价框架，给出了数学核心素养教育评价表，利用多元统计分析方法研究了全国卷的数学核心素养考查特点，并提出了高考命题建议，为基于试卷的核心素养测评研究提供一定的参考．

数学核心素养测评；高考试卷；命题建议

1 问题提出

数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的[1]．

《普通高中数学课程标准（2017年版）》（以下简称“2017版课标”）中提出六大数学核心素养：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析．为了落实学生发展核心素养的目标，新课改优化了课程结构，强调以“主线—主题—核心内容”为结构的教学内容，制定了基于数学核心素养的学业水平，给出以核心素养为重要考查目标的学业水平考试与高考命题建议．

2013年教育部成立专项调研组，对《普通高中数学课程标准（实验）》的实施情况进行了调研工作，反映了课程标准内容与考试命题的脱节现象[2]．这一现象在一定程度上反映出关于命题研究的教学评价工作做得不够充分．为了使新课标中所提倡的“六大核心素养”能够切实扎根教学实践，深度融入考试命题，基于核心素养评价框架的试题测评工作成了研究的重点方向．

近年来，一部分研究者从定性分析的角度进行了数学核心素养测评研究工作．比如，张惠英[3]和姜鹏[4]采用定性分析的方法，从六大核心素养的角度分析了中考试题的命题特点与学生答题情况；何萍等[5]选取6道中考试题，定性地分析了六大数学核心素养考查情况，并给出了数学核心素养教学与评价现状的建议．一些学者建立了数学核心素养评价指标体系，并从定量分析的角度开展了数学核心素养测评研究工作．比如，董林伟等[6]建立了初中核心素养三级指标体系，并利用试卷测评了初二学生的核心素养发展状况；朱娅梅等[7]建立了小学、初中、高中的基于数学核心素养的大规模数学学业水平测试框架，并利用AMOS结构方程模型对测试框架进行了验证性因素分析．李作滨[8]通过定量分析方法研究了2018年高考试卷核心素养考查权重，统计了不同核心素养考查权重，分析了高考命题特点；朱先东等[9]采用多元统计分析的方式研究了2017年浙江省中考试卷中核心素养的考查情况，但分析结果可以继续完善．这里将结合文献[10]提出的数学核心素养评价框架，将李作滨、朱先东等的工作做进一步研究、改进，基于多元统计方法对2019年高考全国卷进行定性和定量分析，并给出试卷命题建议．

2 研究方法

2.1 评价框架的确定

要研究高考命题试卷中对数学核心素养的评价状况，就需要有一套科学、合理的核心素养形成水平划分标准．喻平提出了一种基于知识学习的数学核心素养划分标准，将知识学习分为3个水平，依次为：知识理解、知识迁移、知识创新．

知识的理解包含两层含义，一是指对知识的本质、类属以及与其它知识之间的种种联系的理解；二是指基本技能的形成与发展[10]．也可以解释说，知识理解是指对知识意义、内涵、知识间逻辑关系的理解，在知识的应用中体会和感悟数学方法，进一步加深对知识的认知，并逐步形成数学基本技能．

知识的迁移是指学习者把理解的知识、形成的基本技能迁移到不同的情景中去，促进新知识的学习或解决不同情境中的问题[10]．应该注意到，知识的迁移是知识的综合应用，是比知识理解更高一层次的水平，它是学生将多种知识本质、类属、逻辑联系、方法迁移到新的情境中，解决数学问题或现实问题．

知识的创新是指学习者能够解决一些非常规的开放性问题；或者生成超越教材规定内容的数学知识；或者对问题进行推广与变式得到一个新的问题[10]．知识的创新是新课标中“四能”的体现，从数学的角度发现和提出问题、分析和解决问题，在这个过程中蕴含着丰富的学科思想与方法．

下面构建结构性数学核心素养教育评价表，主要包括评价指标体系、指标权重及评价标准的构建3个方面．

2.2 评价指标体系的确定

2017版课标中提出六大核心素养，按照喻平提出的核心素养划分标准将6个核心素养划分为18个水平层次，创建如下的数学核心素养评价指标体系表（见表1）．

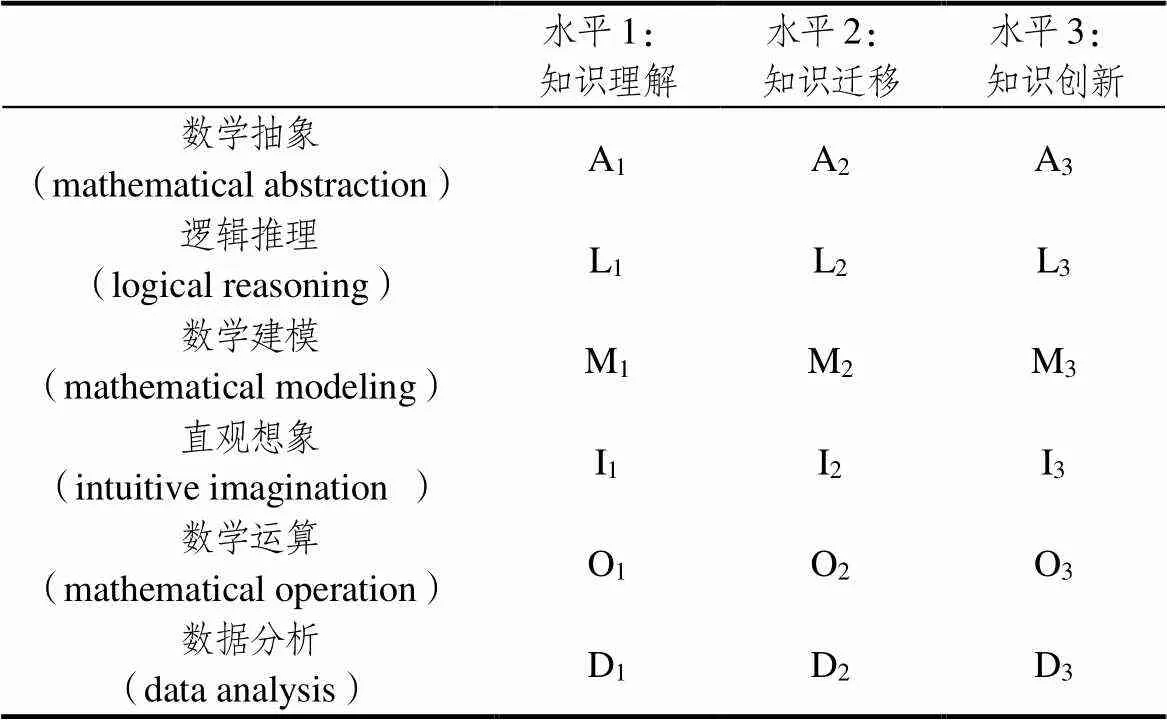
表1 数学核心素养评价指标体系

注：六大核心素养的英文字母与水平层次的组合构成18个素养水平层次的命名．如，A1代表数学抽象素养的知识理解水平．

在阅读新课标中六大核心素养的内涵以及喻平的“数学核心素养评价的一个框架”一文的基础上，提出18个素养水平层次的评价标准．

A1：了解概念、命题、定理、事实、结论产生的缘由；能形成概念体系、命题体系和一定的数学活动经验，体会数学方法；能辨析概念，使用简单知识、基本规则和基本方法了解、解决简单的数学问题．

A2：能在新的情境中抽象出概念、命题、定理、事实、结论等，并用其解决情境问题；能够理解和构建相关数学知识之间的联系，掌握与知识相关的数学思想方法；能够准确运用知识、规则、方法等综合解决常规性复杂问题．

A3：能运用数学抽象的思维提出新的猜想、概念、命题、结论、定理等；能灵活运用概念、命题、定理、方法等解决非常规问题；能够运用具体到抽象的思维来提出、理解、分析问题，认识世界等．

L1：掌握逻辑推理的基本形式（归纳、类比、演绎等），用其证明简单的定理、命题、结论等，并有条理地表述论证过程；掌握基本命题与定理的证明，理解命题体系；有逻辑地思考、表达与交流简单的数学问题．

L2：能在新的情境中通过归纳、类比、演绎等方式进行探索推理，准确表述证明过程，并进一步体会推理的基本形式；理解相关概念、命题、定理之间的逻辑关系，掌握常用逻辑推理方法的规则及思想；在常规性复杂问题中把握问题之间的关联，有逻辑地思考、分析、表达与交流．

L3：从逻辑推理的角度发现和提出命题，并用数学语言予以表达、分析和证明；对于数学问题提出不同的假设前提并形成数学命题；能通过逻辑推理解决非常规的问题；能够用理性精神和有条理、合乎逻辑的思维品质对事物进行判断和分析，认识世界．

M1：掌握高中阶段常见模型（函数模型、方程模型、不等式模型等）的实际背景、数学描述等；了解数学建模的过程，体会模型思想；能运用数学方法和语言构建模型来解决简单的实际问题．

M2：能在新的情境中运用多种知识建立合适的数学模型来解决常规性复杂问题；能够在建立模型过程中进行筛选和优化．

M3：能运用数学思维分析情景中的数学关系，发现或提出问题；利用数学方法和语言建立合适的模型来解决非常规的问题；能够将模型进行推广，用建模的数学方法认识和分析现实问题．

I1：抽象出实物的几何图形，并了解简单图形与实物之间的联系；借助图形性质和变换发现数学规律，利用几何图形直观描述、分析简单的数学问题；能够在用图形描述和表达简单数学问题中体会数形结合方法．

I2：在新的情境中能够运用图形建立起数和形的联系；掌握研究图形与图形、图形与数量之间关系的基本方法；能借助图形与数量的关系理解数学分支之间的联系；能够借助图形探索规律、理解问题、解决常规性复杂问题．

I3：能够通过借助图形提出数学问题，并灵活运用图形解决非常规的数学问题；能够用直观想象探讨问题的本质及其与数学的联系；能够用数形结合的思想去看待和处理现实问题．

O1：能理解运算对象，掌握运算法则及其适用范围，体会运算法则和意义；能运用运算法则和简单的运算技巧进行运算；能用运算结果验证、说明简单的数学问题．

O2：能在新的情境中理解运算对象、探究运算的思路、选择合适的运算方式；理解运算是一种演绎推理，借助运算讨论问题；理解程序思想与计算机解决问题的联系；能综合运用运算法则和运算技巧解决常规性复杂问题．

O3：能够在运算过程中提出新的问题、结论、方法等；能灵活运用运算方法解决非常规运算问题并根据运算结果判断、分析问题．

D1：理解随机现象及简单的概率或统计问题；理解统计中数据收集、整理、分析的方法，并利用其对数据进行收集、整理、描述、分析和推断；理解概率含义并能通过统计方法估计概率；能利用简单概率模型计算简单随机事件概率、解决问题．

D2：在新的情境中，能合理利用统计的方法对数据进行收集、整理、描述、分析与判断；了解随机现象与随机变量的关联，用适当的概率或者统计模型描述规律、解决问题；在运用统计方法中，感悟归纳推理思想．

D3：能够提出随机问题、概率或统计问题；在数据分析中提出关于数据收集、整理、描述、分析的创新型问题；能灵活地运用概率、统计方法解决非常规问题；具有通过数据认识事物、探究规律的品质．

2.3 评价指标权重值的确定

为了对高考试卷做科学定量的分析，需要构建核心素养评价指标权重值．对每一套试卷做详细的分析，结合题目考查知识点、解题方法、实际背景等，综合分析出每道题目所考查的核心素养水平层次，并将题目总分进行对应划分．需要注意的是，一道题目若涉及到多个核心素养考查水平，即根据考查素养的主次在题目总分中划分出多个分数．在此方法下，详细分析了2019年全国文理科Ⅰ卷、Ⅱ卷、Ⅲ卷试题，最终得到了核心素养评价指标权重表，下面以试卷中的几个实例给出详细的操作说明．

例1（2019年全国Ⅰ卷理科第21题）

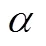
（1）求的分布列；

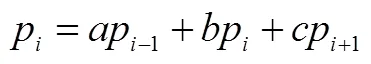
该题为2019年高考理科Ⅰ卷的压轴大题，属于知识创新运用的题目，从科学实验背景出发，将概率与数列等内容巧妙融合，在概率计算、等比数列的证实、利用统计概率知识做出判断的过程中考察学生新情景下知识迁移、采用合理方法解决非常规问题、依据数据分析结果做出合理判断等能力．题目分值设置为第（1）问4分，第（2）问8分．

第（1）问主要考查解决与数学知识相关的情境问题的能力，涉及到在新情景中抽象数学方法，结合情境进行数学运算，属于知识迁移层面．因此，标定相应的指标分数值为：A2–1.5，O2–1，D2–1.5．此处A2–1.5表示该小题考查了知识迁移水平下的数学抽象素养，标定分数值为1.5，O2–1表示考查了知识迁移水平下的数学运算素养，标定分数值为1，D2–1.5考查了知识迁移水平下的数据分析素养，标定分数值为1.5，所有分数值合计为第（1）问总分，4分．

第（2）问第（ⅰ）小问求证数列为等比数列，将数列问题与概率背景相结合，考查新情境下灵活运用知识和方法解决非常规问题，属于知识创新运用层面，标定相应的指标分数值为：A3–1，L3–1，O2–1．第（2）问第（ⅱ）小问判断试验方案的合理性，是利用概率计算结果对问题、方法做出合理地判断，考查学生批判性思维能力和反思能力，属于知识创新运用层面，标定相应的指标分数值为：A3–1.5，O3–2，D3–1.5．

例2（2019年全国Ⅱ卷文科12题）

该题为2019年高考文科Ⅱ卷12题，属于知识迁移运用题目，将圆与双曲线相结合，在离心率的计算中需要学生通过直观作图抽象分析出数学关系、选取合理的计算方法，故而考查学生数学抽象、直观想象与数学运算素养．标定相应的指标分数值为：A2–1.5，O2–2，I2–1.5．

例3（2019年全国Ⅲ卷理科22题）

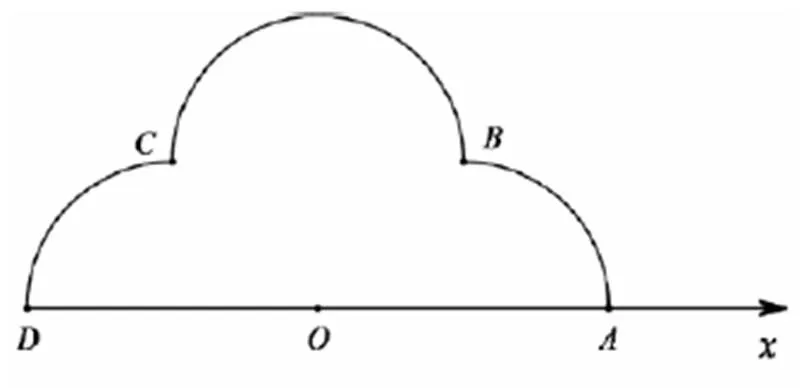
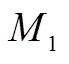
例4（2019年全国Ⅲ卷文科13题）

该题属于知识理解类题目，在计算向量、夹角余弦值时，需要学生回忆向量夹角余弦值的计算公式，并进行简单运算，考查学生使用简单知识、基本规则和基本方法解决数学问题．标定相应的指标分数值为：A1–1.5，O1–2，L1–1.5．

3 研究结果

3.1 2019年高考试卷数学核心素养考查权重表的构建

根据2.2中给出的数学核心素养评价标准对2019年全国文理科Ⅰ卷、Ⅱ卷、Ⅲ卷试题中各个核心素养不同水平的分数进行了标定，并转换成占整份试卷总分的权重（保留三位小数）．见表2（以下简称“数学核心素养考查权重表”）所示．

表2 2019年高考试卷数学核心素养考查权重值汇总表（全国卷）

3.2 基于数学核心素养考查权重表的直观分析

在数学核心素养考查权重表中分别计算了18个核心素养指标权重值在6套试卷中的均值与总和，并汇总了数学抽象（A）、逻辑推理（L）、数学建模（M）、数学运算（O）、直观想象（I）、数据分析（D）六大核心素养的考查权重值．经过讨论分析，得到以下结论．

在一定程度上核心素养考查彰显了数学基本思想．史宁中指出：“把数学基本思想归结为3个核心要素：抽象、推理、模型，数学基本思想是数学核心素养体系的基底．”[11]根据六大核心素养的考查权重均值可以发现，数学抽象素养权重占34.3%、数学运算素养权重占39%、直观想象素养权重占12.4%、逻辑推理素养权重占10.3%．这说明6套高考试卷从数学抽象素养、逻辑推理出发，考查数学基本数学思想．由于高考试卷脱离不了探究运算思路、合理运算的过程，故而数学运算素养占比高达39%，考查学生数学能力．数学建模素养在高考试卷中的考查权重低下，这表明高考试题在考查学生合理、创新利用数学模型解决实际情境问题的能力上表现力不足．值得提及的是，全国I卷理科第4题要求学生估算人体身高值，考查了学生在新情境下综合利用多种知识方法进行数学建模的素养，是一道高考核心素养考查背景下的“亮点题目”．

6类试卷核心素养考查分布基本一致，文理科同素养考查层次彰显差异．绘制出2019年高考试卷六大数学核心考查权重分布图（见图1），由图可知，对于全国6套试卷而言，数学抽象、数学运算素养考查权重值最高，直观想象与逻辑推理素养考查权重值次之，数据分析与数学建模素养考查权重值最低．另外，在同一核心素养考查水平层次上文科试卷相较于理科试卷考查层次较低．比如，理科Ⅰ卷中数学抽象A1水平考查权重为8%，相应的文科为13.3%；数学运算O3水平考查权重为7.1%，相应的文科为1.4%；理科Ⅲ卷中直观想象I2水平考查权重为13.3%，相应的文科为9.5%．

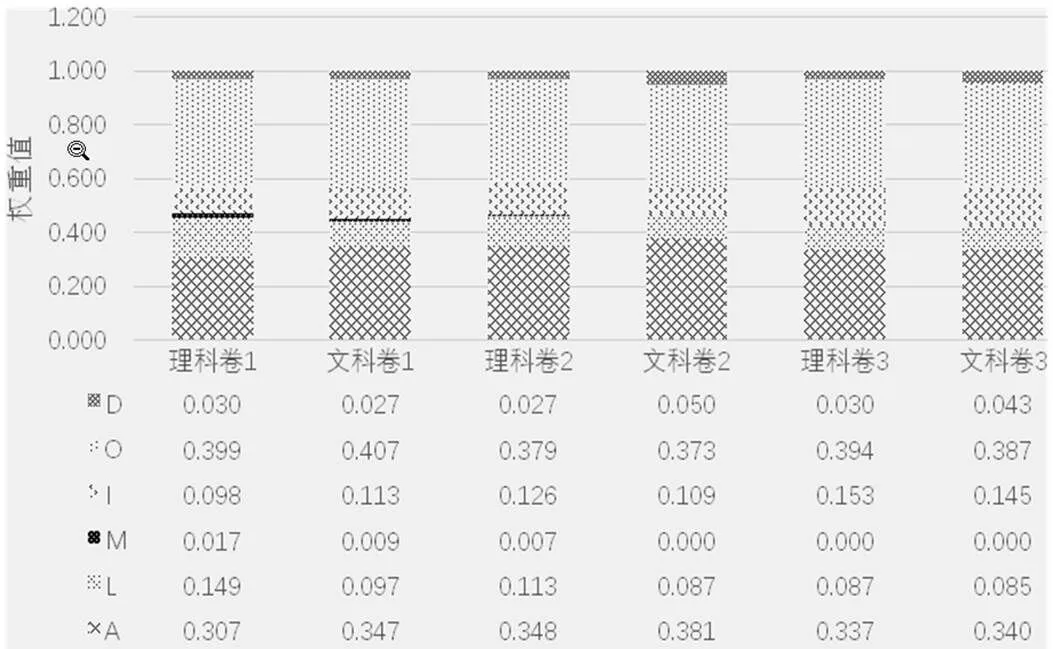
图1 2019年高考试卷六大数学核心素养考查权重分布

知识迁移水平下的核心素养考查为主．根据表2中六套试卷核心素养考查权重值总计数据可知，数学抽象A2、逻辑推理L2、直观想象I2、数学运算O2素养考查权重分别占1.382、0.430、0.518、1.584，占比数量较高，这表明知识迁移水平下的核心素养考查是高考试卷命题的主导方向．同时，试卷中知识创新水平下的核心素养考查权重值虽然较少，但却能够深入考查学生的实践能力与创新能力．

3.3 基于多元统计分析的核心素养考查权重分析

为了进一步探究试卷类型、数学核心素养考查水平层次在空间位置上的区分程度，以及各类别之间的关联程度，采用SPSS24.0对表2中的数据进行对应分析．由于表1中的权重值数据不是频数，而是比率值，故而采取欧几里得距离来代表相应单元格内平均值偏离无关联假设的程度[12]．并得到汇总表（表3）与对应分析图（图2）．

由表3可知，维度一和维度二共解释了83.3%的原信息．通过图2，可以得到以下结论．

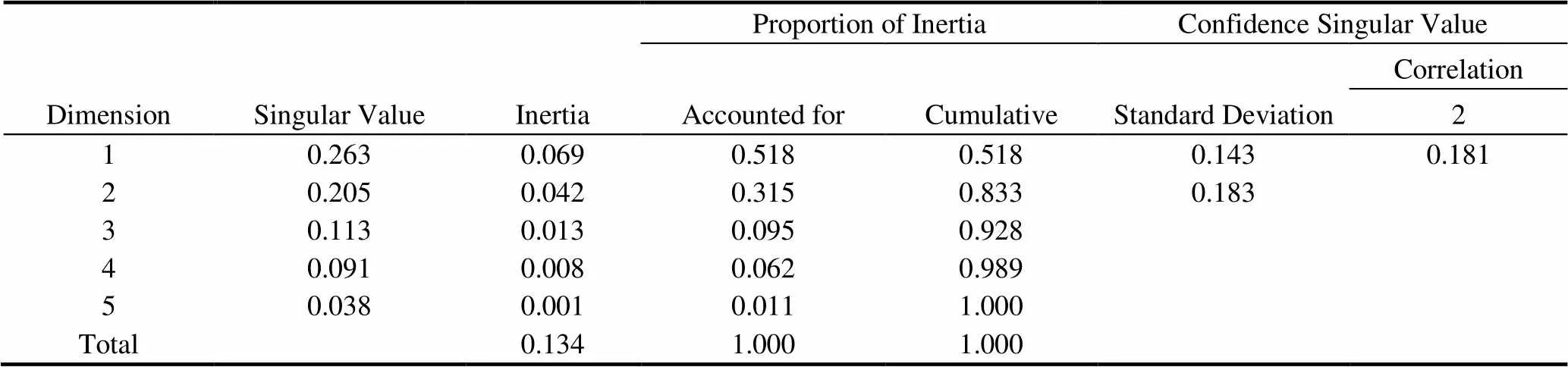
表3 汇总表

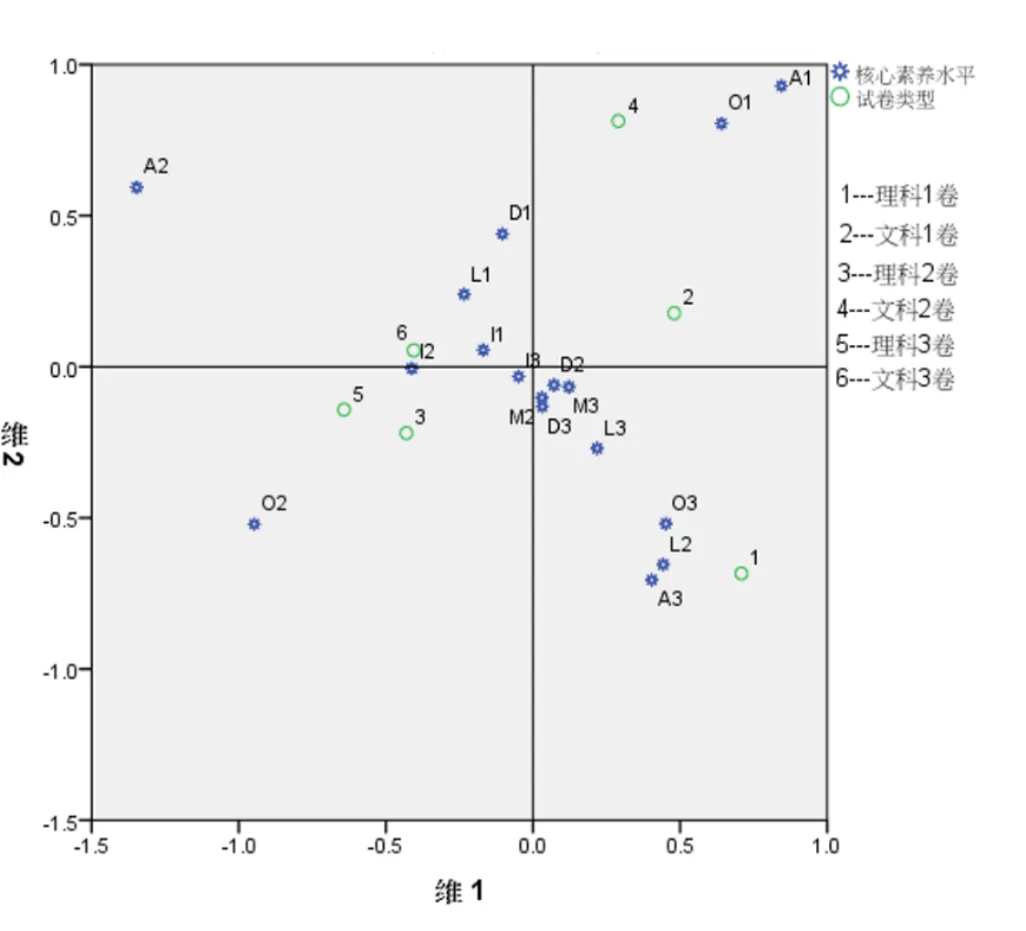
图2 对应分析图

总体上试卷类型、核心素养考查水平两个变量在空间位置上分得比较开，这说明在维度一和维度二上有所区别．但是注意到它们在维度二上的区分度稍微差一些，并且对于核心素养考查水平而言，存在素养分布密集的情况．

6类试卷中理科Ⅰ卷、文科Ⅰ卷、文科Ⅱ卷远离原点，且相互远离，这说明这3套试卷数学核心素养考查水平层次和平均水平相差较大，而且各自特点不同．理科Ⅱ卷、理科Ⅲ卷、文科Ⅲ卷3套试卷的数学核心素养考查水平层次接近．

18个数学核心素养考查水平层次并没有完全分开，其中数学建模M2、数学建模M3、数据分析D2、数据分析D3素养水平距离很接近，说明这4个考查水平是紧密相关的．就数学角度而言，数学模型的构建需要从实际背景入手，建立含参数模型，这当中自然离不开数据的收集和分析．

在对应分析图中，理科Ⅰ卷和数学抽象A3、逻辑推理L2、数学运算O3素养散点的放射线方向一致，则说明试卷素养考查水平高于平均水平．查看表1数据可知理科Ⅰ卷在A3、L2、O3这3个素养上的考查权重是最大的．显然，理科Ⅱ卷、理科Ⅲ卷、文科Ⅲ卷位于A3、L2、O3素养散点的反射线的反方向，则说明这3套试卷素养考查水平低于平均水平，这与表1中的数据吻合．

根据数学核心素养考查指标散点与6套试卷在对应分析图中的分布位置可以对试卷进行分类．第一类为文科Ⅰ卷、文科Ⅱ卷，第二类为理科Ⅱ卷、理科Ⅲ卷、文科Ⅲ卷，第三类为理科Ⅰ卷．

4 讨论及建议

2019年高考全国卷注重知识迁移水平下的数学核心素养的考查，并逐步渗透一些现实问题、数学文化等情境，体现了学生的知识创新能力与数学核心素养，进一步考查学生分析和解决问题的能力．中学生数学核心素养的培养与测评是落实“立德树人”教育根本任务的重要实践方向之一，高等教育入学考试作为检验学生核心素养的一种手段，必定要保证试卷紧扣高考考纲和数学核心素养体系，才能达到考核人才的目的．因此，可以提出一些关于高考命题的建议．

首先，高考命题需要符合中国人才培养目标，因此认真研读相关文件是高考命题的基础．王尚志等指出，21世纪初的高中课程改革，课程方案与考试评价脱节，而2017版课标中提出了考试评价的相关要求[13]．事实上，2017版课标指出：“校内评价或考试、学业水平考试、高考均应以课程方案、课程标准和国家相关教学文件为依据，考试命题应紧密联系社会实际与学生生活经验，探索创设整合的、情境化的真实任务，要有利于促进学生核心素养的发展．”课程标准与教材、教学改革、考试命题之间环环相扣、不可分割，课程标准又作为基础点，指导着教学与考试命题．因此，高考命题应该从课程标准出发，立足现实，考查学生数学核心素养的发展情况．此外，教育部每年会出台各科《普通高等学校招生全国统一考试大纲》，阐明考核目标与考核范围，如在考查数学能力时指出：“以数学知识为载体，从问题入手，把握学科的整体意义，用统一的数学观点组织材料，侧重体现对知识的理解和应用，尤其是综合和灵活的应用，以此来检测考生将知识迁移到不同情境中去的能力，从而检测出考生个体理性思维的广度和深度以及进一步学习的潜能．”[14]因此，高考命题需立足考纲，合理命题，考查学生相应能力与意识．

其次，高考命题要处理好知识理解、知识迁移、知识创新3个水平的关系，聚焦核心素养考查，彰显“立德树人”的育人目标．具体地讲，可以提出一些详细的命题建议．

深度融入数学文化，彰显数学底蕴色彩．谈到数学文化，必然不能忘记中国古代数学．

中国古代有诸多数学人才与数学创造，数学家有祖冲之、秦九韶、杨辉、刘徽等，数学著作如《九章算术》《周髀算经》《海岛算经》[15]．中国古代的数学，可以说在世界上一直居于主导地位并在许多主要的领域内遥遥领先，不仅有诸多领先于世界的算法案例，更蕴含了丰富的数学思想，这样的古代数学素材自然可以融入到高考命题中．中国古代数学以新情境问题出现在高考试题中，利于考查学生数学应用能力，培养学生民族数学认同感．此外，希腊数学、阿拉伯数学、印度数学等中的数学文化内容均可尝试融入到高考试题中，这是拓展学生数学视野，考查学生迁移能力的重要素材．

立足现实情境问题，考查学生创新应用．史宁中认为：“数学的眼光是什么？就是数学抽象．”[16]数学抽象是基于现实世界或者是情境而进行的一种对事物本质、规律、关系进行抽象表征的数学思维过程，是一种数学基本思想．因此，在高考命题中重点考查学生的数学抽象素养是高考改革的方向，而现实情境问题不仅能考查数学抽象素养，更是学生识别新情境，进行知识迁移、创新的载体．此外，学生在现实情境中进行数学抽象、表征问题的过程中会涉及到逻辑推理、数学建模等素养，可以说从现实情境出发的数学问题可以多方位考查学生数学核心素养水平，以及知识的应用与创新意识．

缩小文理试卷差距，融入高等数学基础．《考试蓝皮书：中国高考报告（2019年）》一书中指出：“新高考数学科内容改革的目标是建立文理不分科的数学科统一考试体系，满足高校各专业对考生数学基础知识和基本能力的共同要求．”[17]这是实现文理不分科后高考数学改革的趋势，预示着高考数学试题将融入一定的高等数学基础内容，保证高校专业对数学基础的要求，试卷呈现基础性、综合性、应用性与创新性特点．因此，高考试卷命题要精选考试内容，优化试卷结构，讲求试卷的基础性与综合性，兼顾文理试卷难度，逐步缩小文理科差距，为新高考改革奠定基础．

高考试卷核心素养测评是当前考试评价制度下数学核心素养测评研究的重要方向，这里提供了一些基于统计数据与分析的研究方法和结论，以上所述实属抛砖引玉，阐述如有不当之处，敬请批评指正．

[1] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：4．

[2] 王尚志，胡凤娟．高中数学课程标准“修订思路”“组织”及“过程”[J]．数学教育学报，2018，27（1）：11–13．

[3] 张惠英，王瑞霖．基于核心素养的数学测评研究——以河北省2017年中考数学试题为例[J]．数学教育学报，2017，26（5）：31–35．

[4] 姜鹏．基于“数学核心素养”的中考数学试卷分析——2017年中考数学南京卷评析[J]．中学数学教学参考，2018（15）：62–64．

[5] 何萍，章才岔．基于核心素养视角的数学测评研究——以温州市2017年中考数学试题为例[J]．数学教学通讯，2018（29）：3–5．

[6] 董林伟，喻平．基于学业水平质量监测的初中生数学核心素养发展状况调查[J]．数学教育学报，2017，26（1）：7–13．

[7] 朱娅梅，刘姣，陈林山．基于核心素养的大规模数学学业水平测试框架[J]．教育测量与评价，2018（9）：18–24．

[8] 李作滨．2018年13套高考数学试卷审思：基于核心素养的视角[J]．教育测量与评价，2019（4）：51–57，64．

[9] 朱先东，吴增生．核心素养视角下对数学测评的研究——以2017年浙江省中考试题为例[J]．数学教育学报，2017，26（5）：36–43．

[10] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19–23，59．

[11] 刘祖希．访史宁中教授：谈数学基本思想、数学核心素养等问题[J]．数学通报，2017，56（5）：1–5．

[12] 张文彤，董伟．统计分析高级教程[M]．北京：高等教育出版社，2018：275．

[13] 胡凤娟，吕世虎，王尚志．深度理解《普通高中课程方案（2017年版）》[J]．数学教育学报，2018，27（1）：18–21．

[14] 教育部考试中心．2019年普通高等学校招生全国统一考试数学考试大纲[EB/OL]．（2019–01–31）[2019–07–03]．http://www.neea.edu.cn/html1/report/19012/153-1.htm．

[15] 顾今用．中国古代数学对世界文化的伟大贡献[J]．数学学报，1975，18（1）：18–23．

[16] 史宁中．高中数学课程标准修订中的关键问题[J]．数学教育学报，2018，27（1）：8–10．

[17] 杨学为．中国高考报告（2019）[M]．北京：社会科学文献出版社，2019：105．

Study of Examination Assessment Based on the Framework of Evaluation on Mathematics Key Competencies——A Case Study of National Volume 2019 College Entrance Examination

LI Hua1, 2, HU Dian-shun1

(1. School of Mathematics and Statistics, Central China Normal University, Hubei Wuhan 430079, China;2. Xi’an Chang’an District No.3 Middle School, Shaanxi Xi’an 710100, China)

The assessment of mathematical key competencies was an important method to apprise the effect on the cultivation of students’ core components of mathematical literacy. While college entrance examination was an important way of testing students’ mathematical key competencies, conducting researches on mathematical key competencies based on college entrance examination papers had great significance for the new reform plans of the national college entrance examination. Based on the core mathematics literacy evaluation framework by Yu Ping, the research approaches the national volume 2019 college entrance examination as a sample. This paper draw out an education evaluation scale for mathematical key competencies, studied the characteristics of mathematical key competencies on national volume with multivariate statistical analysis, and put forward some suggestions for the design of the examination questions. This paper could provide some value for the assessment of mathematical key competencies.

the assessment of mathematical key competencies; college entrance examination; suggestions for the question design

G424.74

A

1004–9894（2020）02–0018–06

2019–11–03

教育部人文社会科学研究规划基金项目——中小学核心素养测评的模型建构与实证研究（19YJA880012）；陕西省教育学会2019年度重点课题——高中生综合素质培养与科学评价研究（SJHZDKT201906-01）

李华（1994—），男，陕西汉中人，硕士生，主要从事中学课程与教学论研究．

李华，胡典顺．基于数学核心素养评价框架的试卷测评研究——以2019年高考全国卷为例[J]．数学教育学报，2020，29（2）：1823．

[责任编校：周学智、张楠]