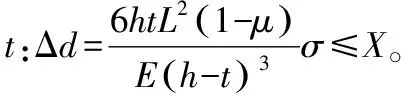金属薄板平面铣削形变分析与控制

苟慎龙，邱吕强，徐刚，郑炜，韩明洋

(中国核动力研究设计院 第四研究所，四川 成都 610005)

0 引言

金属薄板类零部件广泛应用于汽车、船舶、航天、核能等领域，其在军、民生产和生活中占有举足轻重的地位。然而，金属薄板类零部件的加工制造普遍存在形变严重、加工难度大等问题，直接影响产品质量和使用性能。因此，如何有效控制薄板零部件的加工变形，对提高加工质量和生产效率具有重要研究价值。

金属薄板通常由热轧或冷轧工艺制成，初始形态各异，弯曲程度严重，平面加工难度较大。同时，在初始状态下，金属薄板通常都存在较大的残余应力，加工形变严重。因此，薄板零部件的加工过程中对于装夹方式、工艺流程、吃刀深度等加工参数需严格把控[1]。加工实例如图1所示。

图1 金属薄板实际加工状态

1 金属薄板加工形变因素分析

由于在实际加工过程中，金属薄板加工形变量较大[2]，需对金属薄板的形变因素进行分析。金属薄板的加工变形主要包括两个方面：装夹形变和加工形变。

装夹形变主要指工装夹具与工件之间相互作用而产生的形变。该种形变可通过调控装夹点、装夹顺序等有效控制形变量。

加工形变主要包括让刀、热应力形变和残余应力形变。

1) 让刀为材料弹性形变，形变量相对较小且不可避免；

2) 热应力形变为切削热在工件表面形成的应力形变，可通过合理使用切削液，提高切削速度等方式有效调控；

3) 残余应力为材料内部应力，随着加工过程的进行，工件初始残余应力的平衡被破坏，导致板材弯曲变形。残余应力加工形变量只受初始残余应力以及切削厚度的影响[3]。

因此，内部残余应力是造成工件加工变形的主要因素，本文主要针对薄板零件加工残余应力形变进行分析和研究。

2 金属薄板加工形变理论

实际生产过程中，金属薄板厚度远小于长度和宽度。加工过程中，从表面开始逐层铣削，设金属薄板厚度为h，单层铣削厚度为t。沿板材长度方向设为x轴，厚度方向为z轴，金属薄板加工简易模型如图2所示。

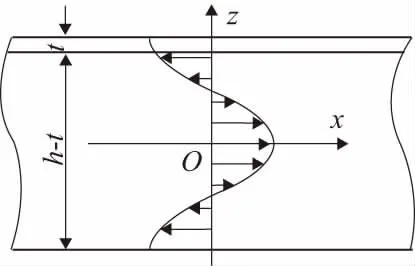
图2 金属薄板铣削模型

根据金属薄板的内应力平衡，应力应变关系以及应变曲率关系，可以得到金属薄板加工过程中的应力曲率关系[4]，如式(1)所示。

(1)

当被剥除第一层材料内平均应力值σx1和σy1已知，可解出z=0处x、y向应变的εx0和εy0及构件x、y向的曲率ρx和ρy。其中，E为材料弹性模量，v为泊松比。

在第一层铣削的基础上进行后面各层的铣削加工，由此可以得到各层材料铣削后的应力曲率关系，如式(2)所示。

(2)

挠度和曲率的几何关系为：

(3)

其中：ρ为曲率；L为长度,mm；Δd为挠度,mm。

3 金属薄板逐层切削模拟仿真

本文以大平面不锈钢薄板平面铣削加工为研究对象，在实验过程中要得到初始残余应力，需获取大量实验数据。为不影响项目工作的正常运行，本文借助非线性仿真软件进行模拟试验[5]。

设置材料弹性模量E=194020MPa，泊松比v=0.3； 沿厚度方向将模型分为16层，单层切削厚度为1mm，加载预设残余应力，分布如图3所示。

在有限元软件ABAQUS中进行仿真试验，测量薄板底面沿长度方向各测量点的z向位移量，并与理论计算值进行对比，位移测量值如图4所示。

图3 初始残余应力分布图

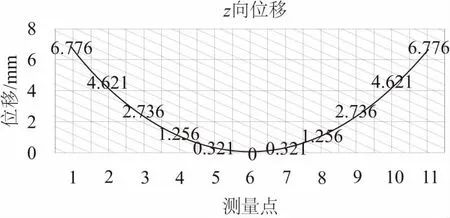
图4 单层铣削z向位移

将图3中设置的初始残余应力带入第2节中理论分析公式，可计算得板材铣削一层理论挠度值为7.03mm，而有限元仿真挠度值为6.78mm，相对误差约为3.75%，依次类推可得铣削n层的挠度理论计算值与仿真值，如图5所示。

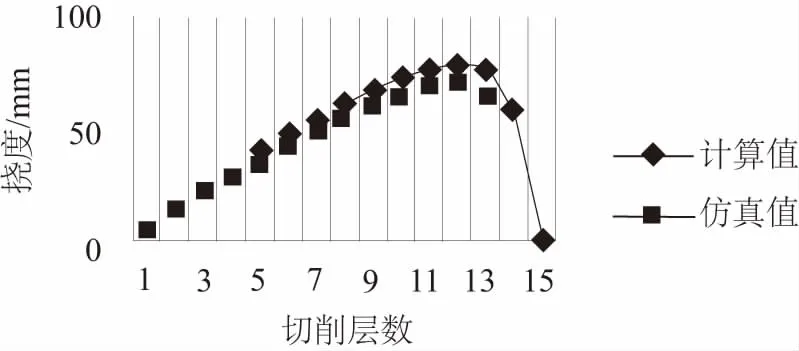
图5 逐层切削理论与仿真对比

由图5可知，随着逐层切削的不断进行，挠度的理论计算与有限元仿真的变化规律基本一致，且因累计误差的影响，随着切削层数的增加相对误差逐渐增大，但总体上相对误差都不超过15%。因此，可证明计算公式的有效性。

4 金属薄板加工形变实验测试

板材轧制长度约为1700mm，厚度约为16mm，属于典型的大平面薄板零件。加工最终厚度为13mm，总体剥除厚度约为3mm，平面度要求0.3mm。在铣削实验过程中，各层铣削厚度根据工件的实际形变状态进行适当微调。由于残余应力的形变影响，逐层铣削实验共分6层，依次为上下表面轮流交替翻面铣削， 沿不锈钢板材长度方向，每间隔170mm取点，用塞尺测量各层切削前后板材剩余厚度和底面与平台间隙，测量数据如表1和图6所示(本刊系黑白印刷，相关疑问咨询作者)。

表1 不锈钢薄板逐层铣削数据统计

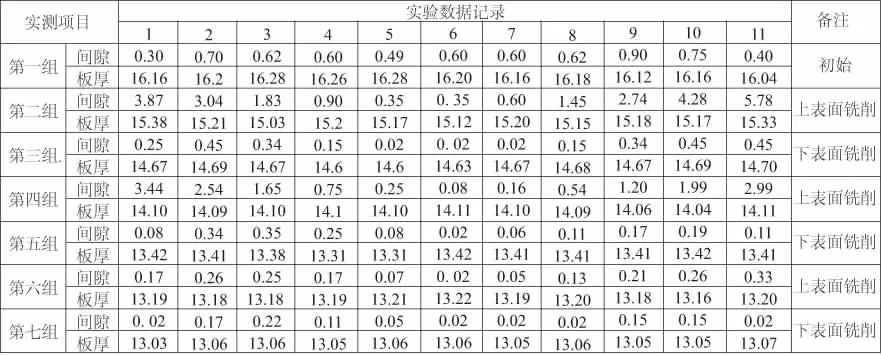
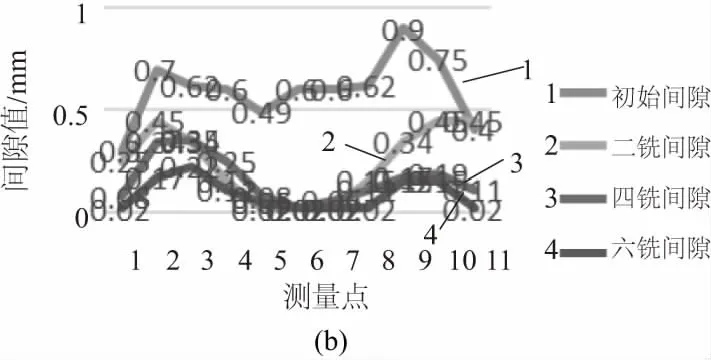
图6 板面逐层铣削数据统计图

由图6可知，板材初始状态较为平整，挠度约为0.3mm。在经过第1次铣削后，不锈钢板呈两端翘起状态，挠度约为4.25mm；经过第2次铣削后，板面回到较为平整状态，挠度约为0.43mm；经过第3次铣削后，板面再次呈两端翘起状态，挠度约为3.13mm；经过第4次铣削后，板面再次回到较为平整状态，挠度约为0.26mm；第5次和第6次铣削，板面形变量较小，满足加工技术要求。

实验结果分析：

a) 板材初始残余应力呈“外压内拉”状态，沿厚度方向对称分布。第一层剥除后，该层压应力被释放，剩余板材为达到新的平衡状态，会出现上表面收缩，下表面伸展的趋势，导致板材两端翘起；第二层与第一层沿厚度方向对称，释放的压应力与第一层释放压应力相互抵消，因此，板面重新回到较为平整状态；同样第三层和第四层铣削结果一致。

b) 由实验结果a) 可知，板材残余应力沿厚度方向由外到内，逐渐从压应力转变成拉应力。因此，在同性残余应力范围内，不锈钢板材板面铣削形变量随铣削厚度的增加而增加。

c) 由初始状态和2、4、6次铣削测量结果可知，板材铣削过程存在边缘效应，板材边缘部分应力较大且分布较为集中，会对板材局部形变状态造成影响，使板材呈M形变状态。

由实验结果分析可知，板材存在显著的边缘效应，计算过程需去除两端数据。此处取第3-9个测量点的数据进行分析计算。根据表1实测参数值，带入式(1)和式(2)中可计算得：

由以上计算结果可以看出：板材初始残余应力基本呈对称分布状态，这也符合板材较为平整的初始状态。因此，可由板材的初始形变状态判断其初始残余应力分布状态。

5 结语

1) 金属薄板的初始残余应力呈“外压内拉”状态，在机械加工过程中单侧释放应力将会造成板面两端相对翘曲；

2) 若金属薄板经过退火或预拉伸处理，初始残余应力较小，在机械加工过程中应尽量保证两侧表面对称等量切削；

3) 若金属板材未经过残余应力预处理，则应根据板材初始形变状态判断残余应力分布状态。如果板材最初呈弯曲状态，则应先铣削凸形面，且凸形面吃刀量应略大于凹形面吃刀量；