电磁发射轨道的温度场及非傅里叶热效应

赵凌康,田振国,靳利园

(燕山大学河北省重型装备与大型结构力学可靠性重点实验室，河北 秦皇岛 066004)

在电磁发射过程中，大功率的脉冲电流通入到轨道和电枢所形成的回路中，可以在极短的时间内将电枢加速至很高的速度[1]。伴随着电枢高速运动，轨道处于大电流、高温、高压和强磁场的工作环境中[2]。而由于电磁热效应引起的温度变化会导致轨道烧蚀、变形，这不利于电磁发射轨道在大功率下的连续发射[3]。因此，了解发射过程中轨道温度分布，以及轨道温度随电枢移动的变化规律，对于轨道冷却系统的设计有着重要的参考意义。

近年来，随着电磁轨道发射技术的快速发展，其所涉及的各种问题的研究都在不断深入。文献[4-6]关注了电磁轨道炮结构的优化及部件的设计，从推进方式、结构设计、和几何参数等方面给出了优化方案，文献[7]分析了发射过程中炮膛内的磁场分布规律，以及电枢距离与峰值磁通密度的关系，并给出了能够有效计算轨道炮智能炮弹部位感应电场和磁场的方法，文献[8-10]关注了轨道材料性能的研究，分析了作为轨道复合层合金材料的电磁、热及力学方面的参数特性，文献[11-13]研究了轨道的强度、刚度、动态响应等问题。尤其是电磁轨道发射时的温度场问题，得到了国内外学者的广泛关注，文献[14]搭建了基于光纤光栅的温度测量系统，测量了导轨多点温度数据，分析导轨上热量分布及传导过程，文献[15]利用有限元方法，对发射中轨道温升这一瞬态过程进行仿真计算，在电磁场与温度场耦合的情况下，求解了轨道横截面的电流与温度分布，文献[16]通过三维数值仿真研究了电磁轨道炮在脉冲波形电流下的电磁场特性，分析了电枢轨道及枢轨接触面的温度变化。从目前的研究成果来看，关于电磁发射轨道温度场的研究主要是通过实验和数值仿真的方式进行分析，理论计算结果还很少见。

本文通过建立发射轨道和电枢的热传导方程，将电流的焦耳热看作内热源，应用格林函数的方法得到温度场的理论解，通过算例分析轨道和电枢的温度分布规律，以及非傅里叶热效应对温度的影响。

1 模型及研究方法

如图1所示，电磁轨道炮由轨道、电枢、盖板等部分组成。建立图2所示的坐标系，其中，d为轨道宽度，b为轨道间距离，在进行温度场分析时，将轨道沿x轴方向离散成等距的N段，其间距均为Δx，轨道沿x轴坐标表达为(x1,x2…xi,…,xj…xN)，轨道总长度为L。电枢滑过每个坐标时将电枢与对应位置的轨道视为一个区块(如图2虚线所示)，整体视为多个区块叠加而成。对于每个区块，其温度场应由如下三部分组成：电枢加热后对轨道的影响；电枢在区块上作用时间内的轨道自身电加热；电枢离开区块后轨道自身的电加热。

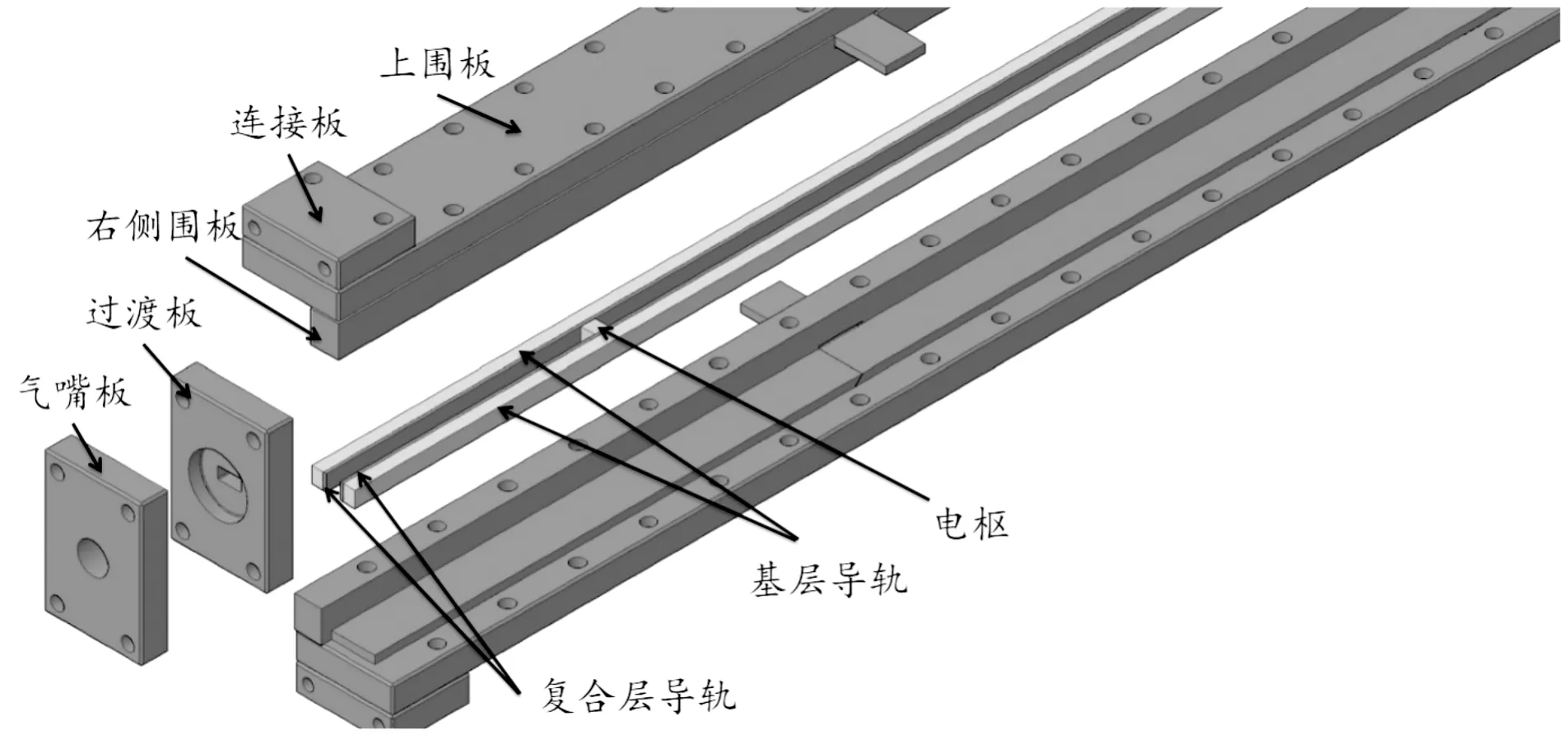
图1 电磁发射轨道炮结构示意图

因此，轨道的温升与电枢移动的位置相关。在tA时刻电枢沿轨道滑动的位移按下式计算[17]

(1)

图2 温度场计算简图

2 轨道温度的计算

因为轨道和电枢升温性质不同，电枢从发射起就开始持续加热，轨道则是在电枢经过后才开始加热，所以将枢、轨加热时间分别表示为tA和tR。将电流发热作为内热源，则轨道与电枢的热传导控制方程为[18]

(2)

其中：λ为热导率；t0为对应材料的弛豫时间；ρ为材料密度；Cp为比热容；g(x)为电加热热源；J表示轨道电流密度，则电加热作用下热源功率为g(x)=J2/σR，考虑到轨道发射情况，则其热源功率可表达为[19]

(3)

其中:U为加载电压；a为电枢沿轨道长度的一半；σA为电枢的电导率；σR为轨道电导率，h轨道厚度；L′为电枢滑过轨道的长度；R0为外接电阻，轨道与电枢接触的热能传递方式视为热传导。

假定轨道初始温度为f1(y)，无外部热流通量，则其初始条件为

T|tR=0=f1(y)

(4)

(5)

考虑轨道与电枢之间进行热交换，即在y=0处轨道边界受电枢热流密度影响，而轨道与外界空气或外包层为绝热，则轨道的初始条件可表达为

(6)

T|y=d=0

(7)

式(6)中:q(tA)表示电枢对轨道边界的热流密度，其值由电枢的温度对y求偏导数得到；tA表示电枢行进的时间，即电枢自加热时间。

式(2)为含热源的非傅里叶导热方程，若忽略热源项，则得如下普适的齐次非傅里叶导热方程

(8)

式(8)的可以通过分离变量法表示为：

T(y,t)=Y(y)·E(t)

(9)

将(9)代入(8)中可得如下两个微分方程

Y″+β2Y=0

(10)

t0E″+E′+αβ2E=0

(11)

将式(10)、(11)的解代入到式(9)中，可得温度场的表达式为

(12)

(13)

当初始条件为常数时，有

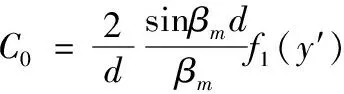
(14)

(15)

(16)

则轨道温度场的解为

cosβmycosβmy′f(y′)dy′

(17)

将式(12)与格林函数解的形式相对应，可以得到本问题的格林函数为

cosβmycosβmy′

(18)

轨道温度场的解为

(19)

其中α=λ/ρCp表示热扩散率。解的第一项表示轨道初始条件的影响，第二项表示轨道自身电加热的影响，第三项表示电枢在该区域上热流密度的影响，体现为非齐次边界条件。但该解在边界y=b上不收敛，应对最后一项做分部积分，用等价的封闭形式代替，令

(20)

对(20)进行分部积分可得：

(21)

其中g2为电枢热源功率，将式(20)、(21)代入到(19)中即可得出轨道温度场的解。

3 电枢温度的计算

在轨道温度场的解析解中含有电枢对轨道边界的热流密度项，故需求电枢的温度场，然后用电枢的温度场对y求偏导可以得出电枢对轨道的热流密度

(22)

电枢在电磁作用下的热源功率为

(23)

应用式(8)来求解电枢温度场，假定轨道电枢温度为f2(y)，其初始条件为

T|tA=0=f2(y)

(24)

(25)

若不考虑电枢与外界的热交换，则电枢边界条件为

(26)

T|y=-b=0

(27)

电枢温度场的解为

(28)

将式(28)代入到式(22)中，即可得到轨道边界热流密度，进而得到轨道温度场的完整表达式。

为了对比非傅里叶和傅里叶效应计算结果的区别，按照同样的条件给出轨道在仅考虑傅里叶效应时的温度场计算结果，傅里叶传热的控制方程如下

(29)

边界条件同式(6)、(7)，(24)、(25)。用格林函数解法可以得到如下解析解

(30)

4 算例分析

取轨道总长L=3 m，轨道上每段区域长Δx=0.02 m，电枢的尺寸为0.2 m×0.2 m×0.2 m，导轨间距b=0.2 m，导轨厚度h=0.2 m。电枢材质为铝，电导率为σA=3.6×107(Ω·m)-1，密度ρA=2 700 kg/m3,传热系数λA=238 W/(m·℃)。轨道材质为铜，电导率σR=5.88×107(Ω·m)-1，密度ρR=8 900 kg/m3，比热容c=386 J/(kg·K)。传热系数λR=377 W/(m·℃)。轨道电感梯度Li′=0.451 24 μH/m，电枢初始温度设为30 ℃，轨道初始温度设为20 ℃，材料的弛豫时间t0=1×10-5s，系统加载电压U=8 000 V，不计摩擦。

图3表示用非傅里叶和傅里叶的计算公式，分别计算得到的电枢内y=0-m处和y=-0.05 m处的温度随电枢在轨道内滑动时的变化曲线，可以看出，在同一时刻越靠近边界即坐标轴，温度越高。并且，对于电枢温度，非傅里叶和傅里叶计算的结果差距并不明显。

图3 l=0- m与l=-0.05 m处电枢温度随时间变化曲线

图4为电枢到达xi=1 m时，对应位置的轨道沿宽度方向的温度分布曲线，可以看出电枢在同一时刻同一位置时，按照非傅里叶效应计算轨道的整体温度场结果比傅里叶计算的结果值略大，这是因为考虑到材料的弛豫效应，造成温度传递的延迟，体现为非傅里叶热传导时轨道的局部温度相对较高。

图4 电枢在xi=1 m处轨道温度沿y分布曲线

图5为电枢从xi=1 m分别移动到xi=1.2 m，xi=1.4 m时，轨道上xi=1 m处的温度分布变化曲线。可以看出，在电枢离开后，原位置继续电加热会引起该区块内温度继续升高。

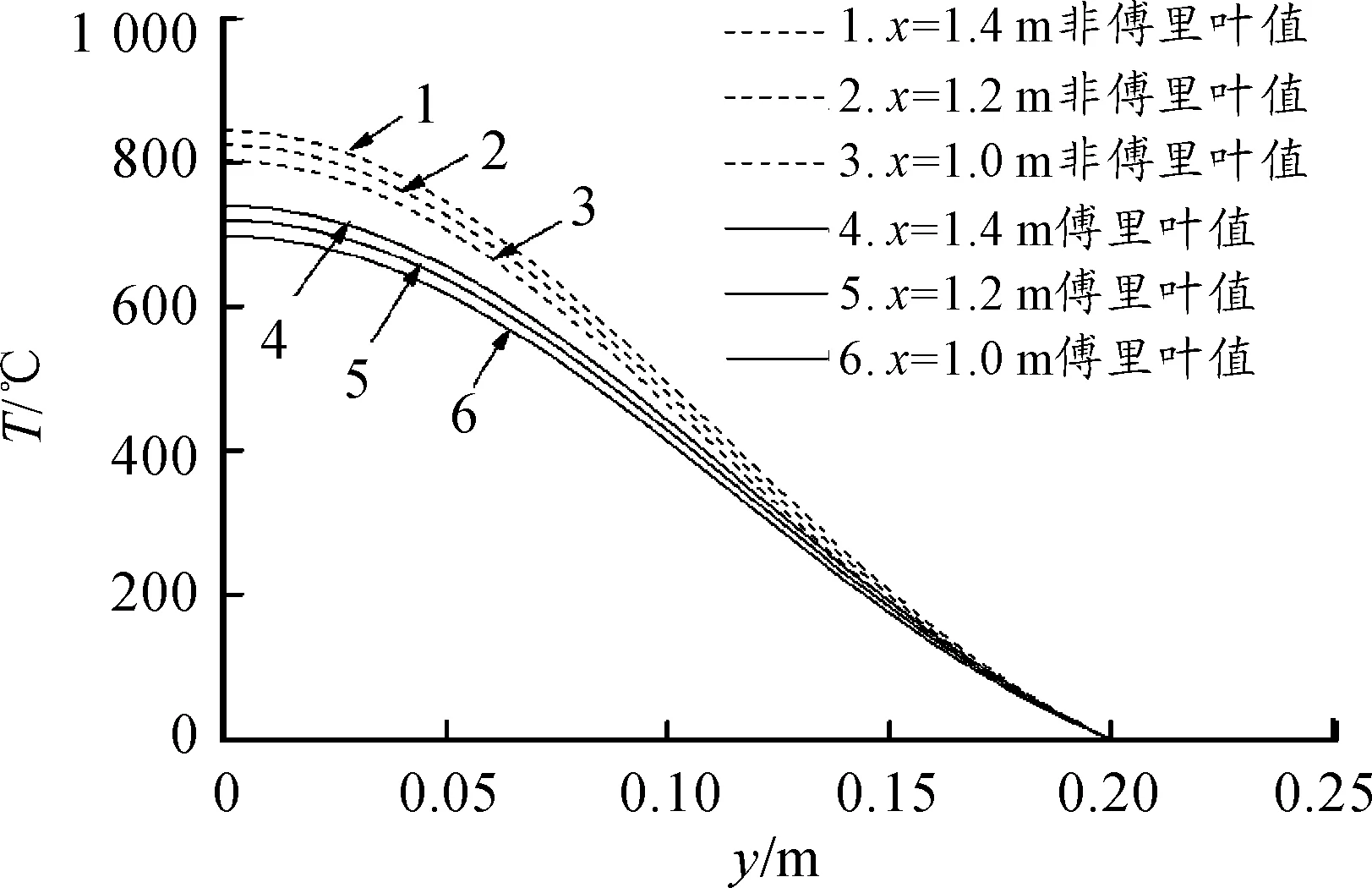
图5 电枢在xi=1 m处继续移动轨道温度沿y分布曲线

图6为电枢分别移动到xi=1.2 m，xi=1.4 m时，轨道上xi=1 m处轨道电加热的温度分布曲线，可以看出，对于非傅里叶和傅里叶两种算法，电加热影响项计算的结果几乎相等。造成这种现象的原因是，电枢极快滑过这两个位置，在一个对应轨道区块内，对于轨道整体温度场加热时间极短，边界y=0+m处热扰动还未来得及传递。

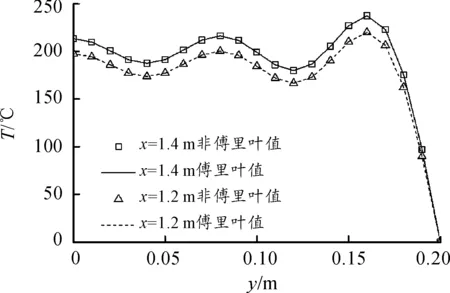
图6 电枢在xi=1.2 m和xi=1.4 m轨道自身电加热影响曲线

图7为当电枢移动到xi=2 m时，对应位置的轨道温度场分布曲线。与图4相比，在轨道内侧y=0+m位置上按照非傅里叶效应计算轨道的温度场结果比傅里叶计算的结果差值明显增加，而远离边界位置的计算结果趋于一致。造成这个结果的原因是，在轨道末端，电枢运动速度极快，对应的这个区块的轨道自身电加热时间极短，轨道内部温度较低，轨道外表面为绝热条件，与电枢接触表面受到电枢的快速、高温差的热冲击。

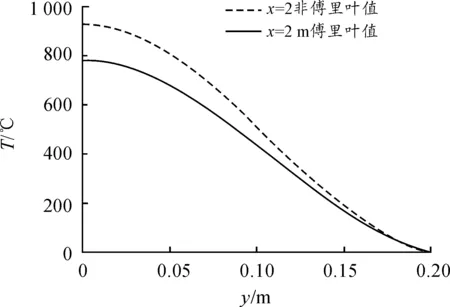
图7 电枢在xi=2 m处轨道温度沿y分布图

图8为轨道与电枢接触面上不同位置处的温度随时间变化曲线。可以看出电枢从初始位置开始移动到轨道终点的过程中，引起xi处轨道内表面y=0+m位置的温度变化。其中，线1、2分别表示在xi=0.5 m处非傅里叶效应和傅里叶效应计算对比的结果，其含义是电枢在未到达指定区域时，轨道一直保持初始温度，电枢到达后边界温度瞬间有一个阶跃，可以看出，两种计算方法在电枢到达该区块瞬间，轨道内表面温度存在阶跃差值。线3、4、5、6、7、8分别表示在xi=1 m，xi=2 m及xi=2.5 m位置时两种计算方法的温度变化，可以看出，随着电枢运动时间的增加，两种方法计算的轨道内表面温度的阶跃差值不断增加。造成这个结果的原因是，随着电枢移动的距离增加，电枢表面y=0-m的温度不断增加，而电枢还未滑过的部分轨道还未形成通路，始终保持初始温度，当电枢温度与轨道温度差越大时，对轨道内表面引起的温度阶跃差值越大。

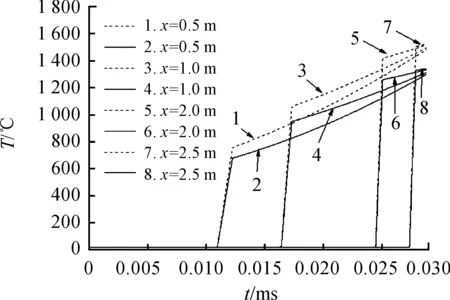
图8 轨道内表面y=0+m处温度随时间变化曲线

图9为电枢运动过程中对轨道xi=1 m和xi=2 m两个位置由热流密度产生的影响曲线，可以看出，对于各个相等的(x=0.02 m长度的区块，随着电枢温度的增加，轨道边界的热流密度同时增大，由非傅里叶效应和傅里叶效应计算的对温度场影响的差值也增大。

图9 电枢在xi=1 m和xi=2 m处热流密度影响曲线

5 结论

1)靠近发射端的轨道加热时间长，电枢对温度影响较小；而出口端的轨道加热时间短，电枢温度相对较高，对轨道的影响显著。因而，靠近轨道发射端的温度高，沿宽度分布均匀，靠近出口端的温度值相对较低，沿宽度分布不均匀，靠近与电枢交界面处的相对较高。

2)由非傅里叶热效应计算的电磁炮发射时的温度场与傅里叶定律计算的温度场存在差值。电枢的非傅里叶热效应并不明显，而轨道的非傅里叶热效应则较为显著，尤其是在靠近出口一端，这是因为持续加热的电枢温度较高，速度较快，与轨道进行热交换的时间短、温差大。