基于最优神经网络结构的故障诊断模型
2020-04-22张保山杨博帆
张保山,周 峰,张 琳,张 搏,鲁 娜,杨博帆
(1.空军工程大学,西安 710051;2.92095部队,浙江 台州 318050;3.93142部队,成都 610041)
故障诊断其作为模式识别的一个重要应用领域,融合了图像处理、证据推理、模糊数学等多个领域的技术,虽然其已发展了近30多年,但“故障诊断学”还是近几年发展起来的。尤其,随着近些年人工智能的兴起,深度神经网络在故障诊断领域的应用变得越来越广泛[1-3],其在非线性、自适应学习原始数据特征,有效挖掘大数据潜在信息,获取较高识别精度方面具有绝对的优势[4-9],但深度神经网络仍然存在运算时间长,参数设置依靠经验从而导致运算效率降低,参数设置缺乏理论依据的问题,困扰着深度神经网络在故障诊断领域的进一步发展[10-11]。
群智能算法(Swarm Intelligence,SI)是采用随机优化策略进行优化的一类算法,具有良好的全局寻优能力,因此,许多学者将SI作为优化人工神经网络的学习算法,如晏福将混沌理论引入灰狼算法,并应用于多层感知器的训练[12];张长利采用遗传算法训练多层前馈神经网络实现番茄成熟度的自动判别[13];雷彦森利用遗传算法优化的BP网络实现对天气的预报[14],但这些方法都只是在确定的神经网络结构,激活函数和优化函数的前提下,对神经网络的连接权值和偏置量进行优化,既不能保证其连接权值和偏置量在全部可选的网络结构上达到最优,且其网络结构、激活函数和优化函数是否选择合理也缺少理论支撑。并且,故障特征往往呈现出多重性、多耦合及模糊性的特点[15-16],若仅仅依靠研究人员的主观经验设置神经网络结构,既会浪费大量人力资源,又难以保证装备维护保障的效率。
深度前馈网络(deep feedforward network,DFN),能够以任意精度逼近任意连续函数及平方可积函数,而且可以精确实现任意有限训练样本集。其通过简单非线性处理单元的复合映射,可获得复杂的非线性处理能力[17-18]。
因此,本文针对深度神经网络在故障诊断方面所存在的问题,将自适应遗传算法和深度前馈网络相结合,提出一种可以根据数据特征动态调整深度神经网络参数的故障诊断模型——基于自适应遗传算法优化的深度前馈网络故障诊断模型。
1 自适应遗传算法优化的深度前馈网络的组成
1.1 深度前馈网络
深度前馈网络(deep feedforward network,DFN),简称前馈网络,其各神经元分层排列,同一层的神经元之间没有相互连接,每个神经元只与前一层的神经元相连接,接收前一层的输出,并输出到下一级,直至输出层。其中第一层称为输入层,最后一层为输出层,中间为隐含层,如图1所示。根据柯尔莫哥洛夫理论可知,一个含有两个隐藏层的DFN络就可以逼近任意非线性函数[19]。
1)正向传递
正向传递,即按照输入层、隐含层、输出层的顺序向前传送,最终在输出层输出yo与真实输出yt进行比对,若其误差δy小于所期望的误差,则训练结束。
如图1所示,输入节点数为t,分别为X1,X2,X3,…,Xt;第一个隐含层的节点数为m,分别为h1,h2,…,hm;第n层隐含层节点数为r,分别为H1,H2,…,Hr;输出层为y,各层间的权值矩阵为长度不固定的横向量wi={wi1,wi2,…,wij},其中i为DFN隐含层的层数,j为各层的节点数,激活函数为f(x)。

图1 深度前馈网络结构图
若采用sigmoid函数,则各隐含层节点的输入为:
Input=w0+w1x1+…+wtxt
(1)
各隐含层节点的输出为
(2)
2)反向传播
反向传播,输出层根据所输出的误差δy反向推算上一层的误差,以此方法计算出每一层的误差,修正各层神经单元的权重,直到输出层最后所得的误差δy缩小至期望误差或达到学习次数[20]。
δy=yo(1-yo)(yt-yo)
(3)
式(3)中:δy为输出层误差;yo为实际输出;yt为期望输出。对于隐含层节点其误差函数为:
(4)
式(4)中:δhi表示隐含节点hi的误差;hiout表示第i层隐含层的输出值;wij表示第i层隐含层到下一层第j个节点的连接权值;δij表示第i层节点到i+1层第j个节点的误差。
1.2 自适应遗传算法
遗传算法(Genetic algorithm,GA)是依据达尔文进化论中“优胜劣汰”思想衍生而来的一种择优算法,其通过对原始种群进行选择、交叉和变异等多次迭代操作,最终获得最优个体[21]。但GA的交叉概率pc和变异概率pm的设置均需依靠操作者经验来决定,若pc与pm设置不合理,GA的收敛性和其最优解的准确性均会受到影响,因此本文采用交叉概率pc与变异概率pm能够自适应调整的遗传算法(AGA)来确保种群的多样性,其中能够自适应调整的pc与pm为:
(5)
(6)
式(5)、(6)中: Δf的含义为每个染色体个体的最大适应度值和平均适应度值的差值;φ1和φ2表示调整速率[22]。
2 自适应遗传算法优化的深度前馈网络的构建
AGA优化的DFN的中心思想也同其他智能算法优化神经网络的中心思想相同,都是要找到被优化神经网络的初始权值和偏置量,但本文所提出的优化方式是:通过找到被优化神经网络的最合理网络结构、激活函数和优化函数,来间接地找到其最优权值和偏置量,不仅达到了优化其结果的目的,更为神经网络参数的设置提供了依据,并综合考虑了遗传算法在进行择优的过程中交叉概率pc和变异概率pm的设置依靠操作人员经验所导致的寻优效率不高的问题,故将自适应pc与pm引入原始遗传算法中,得到全局寻优能力更强的自适应遗传算法。
AGA优化DFN具体流程如图2所示。

图2 自适应遗传算法优化深度前馈网络流程图
步骤如下:
步骤1结合所研究的具体问题,人工预设DFN隐含层层数预选值,隐含层节点数预选值,激活函数预选项及优化函数预选项[23]。
步骤2若存在预置DFN参数,则随机选择一组DFN结构选项及连接权值和偏置量,并将其连接权值和偏置量作为AGA的初始种群。
步骤3将DFN运算所得的损失函数定义为适应度函数,即:
(7)

步骤4计算各染色体的适应度值Fi,并定义每个个体的适应度值Fi与所有个体的适应度值之和的比值为其遗传到下一代的概率,即:
(8)
式(8)中:Fi为种群种个体i的适应度值;s为种群个数。
步骤5自适应pc决定了交叉操作发生概率的大小,并通过在旧种群选择“爸爸”和“妈妈”个体进行交叉操作,产生新个体遗传到下一代种群中,即:

(9)
式(9)中:r为[0,1]的随机数;gk1j,gk2j分别为k1和k2个体在第j维的基因。
步骤6自适应pm决定染色体i发生变异的概率,通过变异操作随机选择染色体i上的若干基因进行修改,增强种群的适应度。

(10)
式(10)中:r1≥0.5和r1<0.5为随机数;s为当前迭代次数;smax为最大变异次数;gmax和gmin为染色体i上基因gij的上、下边界。
步骤7适应度值若满足算法开始前设置的提前结束条件,则修正DFN中的隐含层层数,各隐含层节点数,激活函数和优化函数等参数,若不满足则返回步骤4,重复上述操作。
步骤8当步骤7结束后,利用AGA所求得的最优个体对DFN的初始参数进行更新,则DFN从输入层开始逐层进行训练,直至每一层均训练结束,此时各层的权重值wi={wi1,wi2,…,wij}及其偏量值w0={w10,w20,…,wi0}均已确定,并从预置DFN参数组合集合中删除该组预置DFN参数组合。

步骤10判断是否还存在预置DFN参数组合,若存在预置DFN参数组合,则返回步骤2,重复上述操作;若不存在预置DFN参数组合,则对比之前用各种参数组合训练所得到的误差,将误差最小的DFN参数组合作为选定的网络结构,并将AGA寻优得到的最佳连接权值和偏置量作为DFN的初始连接权值和偏置量重新进行训练,最终输出其识别精度。
3 实验验证及分析
常见的故障诊断数据大致可分为两大类—故障部件的图片以及传感器的检测信号,因此,本文实验内容分为两个部分,分别为图像处理与故障信号处理。对于图像处理部分,本文采用公开数据集,验证本模型的有效性;对于故障信号处理部分,本文采用模拟仿真的方法,验证本模型的有效性。针对图像处理部分,本文将所提出的自适应遗传算法优化的深度前馈网络(AGADFN)与遗传算法优化的深度前馈网络模型(GADFN)和DFN进行对比,此时的DFN因为无法确定其具体结构用GADFN迭代一次的网络代替。以MNIST和CIFAR10标准测试集为实验验证数据,按照9∶1的方式划分训练数据集与测试数据集,采用MD5进行编码操作,将隐含层层数,各隐含层节点数,优化函数和激活函数设置为种群中的个体,其中隐含层层数可选值为{1,2,3,4},各隐含层节点数可选值为{64,128,256,512,768,1 024},激活函数选项为{relu,elu,tanh,sigmoid},优化函数选项为{rmsprop,adam,sgd,adagrad,adadelta,adamax,nadam},每一代种群中的个体设置为20个,迭代次数为10代,自适应调整速率为1,在显卡均为GTX1060硬件条件下,验证结果如图3、图4所示。

图3 实验模型测试MNIST数据集准确率

图4 实验模型测试CIFAR10数据集准确率
由图3可知,随着迭代次数增加,在MNIST数据集上AGADFN精度不断提升,从初始的80.24%提升至99.03%,并且AGADFN经过3次迭代精度便达到90%以上,而GADFN需迭代7次,但在第10次迭代后两种模型在MNIST数据集上测试精度相差不到1%,运行时间上GADFN为6小时1分35秒,AGADFN为5小时41分57秒。
由图4可知,随着迭代次数增加,在CIFAR10数据集上AGADFN精度不断提升,从初始的44.34%提升至63.39%,并且AGADFN在第6次迭代精度便达到57.19%,而且GADFN在第10次迭代精度才达到56.12%。但AGADFN在第10次迭代误差还有36.61%,运行时间上GADFN为7小时56分59秒,AGADFN为6小时33分11秒。
对比分析两组数据得:
1)本文所提出的AGADFN故障诊断模型,在运算速度及精度方面均优于DFN和GADFN,且相比运算精度提升0.47%和12.95%,其运算速度提升5.4%和17.6%,提升幅度更大。
2)本模型在处理复杂数据CIFAR10时,其运算速度提升幅度17.6%及运算精度提升幅度12.95%,相比处理简单数据MNIST时,其运算速度提升幅度5.4%及运算精度提升幅度0.47%,提升效果更加明显。
3)在处理复杂数据集CIFAR10时,AGADFN相比GADFN分类精度提升明显,说明自适应遗传算法寻优能力明显强于遗传算法;在处理较简单的测试集MNIST时,AGADFN相比GADFN虽然收敛速度更快,但在后几次迭代中,精度提升幅度较小,此现象应为遗传算法及其衍生算法本身的缺陷所致。
针对故障信号处理部分,本文采用图5所示的国际标准CSTV滤波器仿真电路,其参数设置如表1所示,其中kΩ和nF分别为电阻阻值以及电容的电容量,故障元器件选择为R5,模拟因为老化导致R5阻值变大所导致的故障,以R5阻值的不同区分故障的程度,R5故障等级及其故障值如表2所示。通过PSpice软件进行仿真实验,共采集数据100组,其中80组作为训练样本,20组为测试样本,迭代次数设置为300次,其余设置与图像处理部分实验相同,比较GADFN与AGADFN的实验误差[24]。
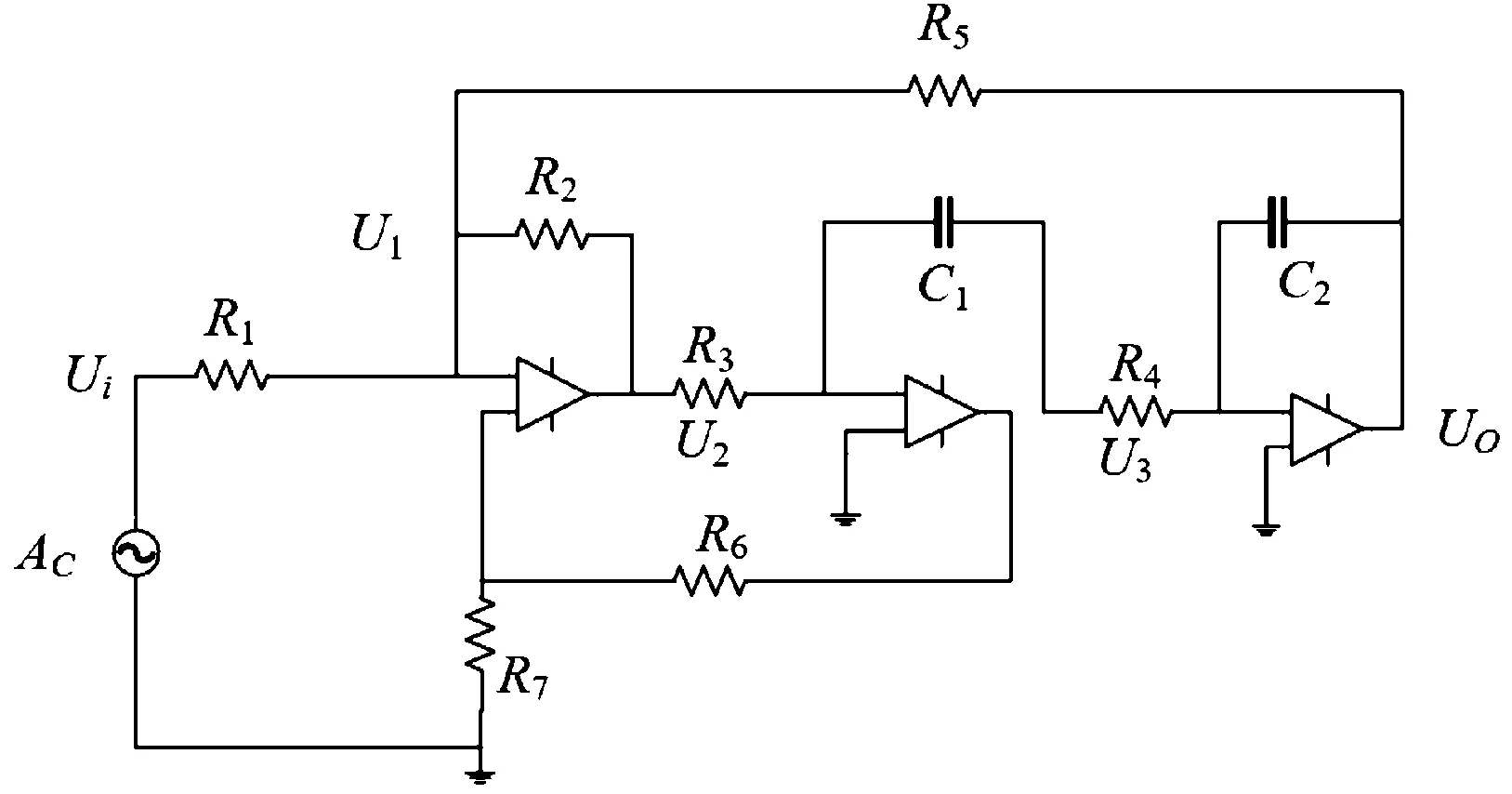
图5 CSTV仿真电路图

表1 CSTV仿真电路参数设置

表2 R5故障等级及其故障值
实验模型测试CSTV数据误差如图6所示,由图6可知,随着迭代次数增加,在CSTV仿真数据集上AGADFN精度不断提升,从初始的82.312%提升至99.994%,并且AGADFN在第127次迭代精度便达到99.973%,而GADFN在第300次迭代精度才达到99.971%;在收敛速度方面,AGADFN在第16次精度为99.948%,GADFN在第26次精度为99.950%,AGADFN相比GADFN收敛速度更快;在稳定性上,AGADFN在迭代200次以后误差便趋于稳定,而GADFN在迭代200次以后,误差依然存在较强的波动。

图6 实验模型测试CSTV数据误差图
总结以上数据分析结果,本文所提出的ADGADFN故障诊断模型在运算速度及精度方面均提升明显,且处理复杂数据能力更强,且通过此类方法优化模型的分类能力主要取决于所选择的群智能算法的全局寻优能力,因此本文所提出的这一类故障诊断模型诊断能力的提升,可通过增加迭代次数或改良群智能算法进一步解决。
4 结论
本文所提出的自适应遗传算法优化的深度前馈网络故障诊断模型比原始深度前馈网络故障诊断模型计算精度有所提升,实际调试时间短,优化方法更为合理。但是还存在以下问题:其一,本文所提出的模型虽然不需要反复进行人工的参数调试,在训练网络方面节省了大量时间,但运算时间长,对简单的故障诊断效率不如浅层神经网络高,后期可以试着通过多GPU数据并行框架对其运行速度进行优化;其二,本模型没有充分发挥神经网络鲁棒性强、适应度高的优势,后期考虑将本模型结合远程信息采集系统,应用于远程故障诊断系统,提高故障诊断的效率[25]。
