前冲击发减后坐方案对某榴弹发射器射击密集度的影响

廖章俊，王 涛，宋 杰，廖振强

(南京理工大学 机械工程学院，南京 210094)

战场上新型装甲车辆的机动性、防护力、威力和最大射程都会得到加强[1]。榴弹发射器作为主要针对性武器，降低后坐力能为提高射击威力和实现轻量化提供更多空间。

在枪机后坐系统中，采用前冲击发技术可以利用复进撞击来消耗前一发弹所产生的后坐动能，有效减小武器系统后坐力。前冲击发原理的应用始于1957年美国的XM204型前冲炮[2]，在减后坐方面取得了较好的效果，各国开始争相研制[3-4]。我国于20世纪70年代首次将冲击发原理应用于130mm加农炮上，随后国内学者对前冲击发方式的自动武器做了一些系统性的研究。理论研究表明前冲击发原理可以将后坐力减小75%[5]，并成功将前冲击发原理应用于自动武器上来降低系统后坐力[6-8]。

但是目前基于前冲击发原理的自动武器研究存在三个主要问题：往往侧重于前冲击发原理对系统的减后坐效力分析而忽略了对射击精度的影响；虽然成功将前冲击发原理过渡到自动武器上，但是前冲击发结构与自动武器本身结构的最优化结合都很浅显，没有系统的研究方法；研究对象初速普遍处于低音速状态，急需适应未来战场的射程远、火力猛、威力大的自动武器。

本研究设计了一种将前冲击发原理应用于某高初速榴弹发射器的减后坐方案，弥补了目前前冲击发原理应用于自动武器时存在的主要不足。虽然自动榴弹发射器对射击精度的要求不是很高，但枪管作为参与浮动的一部分其身管振动会比较剧烈，膛口跳动较大，导致射击精度下降显著，不容忽视。研究前冲击发结构参数对身管振动的影响，合理采用前冲击发结构参数，可以改善武器射击精度。

1 武器系统减后坐原理

图1为某前冲击发原理减后坐高初速榴弹发射器原理示意图。

图1 减后坐原理示意图

如图1所示，扣动发射器扳机后，机框开始复进，并完成进弹、闭锁动作，同时拨弹板复位准备抓取下一发弹；机框在复进时推开以扭簧连接于机匣的枪管锁扣，此时枪管不再处于固定状态，与枪机组件共同复进前冲；当前冲速度最大时火药点火，发射药剧烈燃烧，推动弹丸前进，同时产生的后坐冲量优先被前冲复进的动量抵消一部分，在弹丸到达导气孔之前，残余后坐冲量仍旧带动闭锁的自动机后坐；在弹丸经过导气孔以后，一方面导致枪机同导气式自动机一样正常开锁并后坐到位，另一方面，迫使枪管减速并复进直至复进到位时被枪管锁扣卡住并等候下一发射击时机框在复进过程中推开枪管锁扣解锁。

2 系统发射动力学模型

2.1 模型简化及载荷处理

采用前冲击发减后坐方案的榴弹发射器射击时的实际影响因素复杂多变，需要进行一定的简化处理，以便于计算分析得出仿真结果，但过度的简化可能会忽略掉关键的影响因素，导致结果失真与实际情况完全不符。本研究在采用前冲击发减后坐方案的榴弹发射器中所作的简化假设如下：武器系统的零部件繁多而且结构复杂多变，对于质量很小而且不影响武器系统射击循环过程的小部件不予考虑；对于质量较大但是不影响武器系统射击循环过程的大部件以等效质量替换；武器系统的受力情况复杂，对于结构中的前冲簧、复进簧、架座簧等弹簧部件均以有质量和阻尼的弹性系统替代；对于脚架与土壤的连接、射手与抵肩的连接均以集总参数模型替代；对于影响武器系统方位方向运动的供弹系统以计算阻力曲线输入；对于弹药制造工艺带来的误差予以忽略，每次射击循环的内弹道过程均一致。

2.2 载荷计算

前冲击发减后坐方案的榴弹发射器的初始计算条件如表1～表3所示。

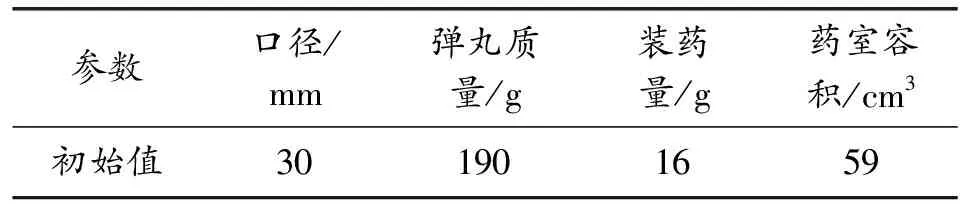
表1 榴弹主要初始参数

表2 导气室主要初始参数

表3 前冲击发结构主要参数

通过Matlab对采用前冲击发减后坐方案的榴弹发射器的内弹道过程与后效期过程进行编程求解，获得武器系统单发时的膛内压力、导气室压力、制退力、弹丸速度的变化曲线如图2～图4所示。

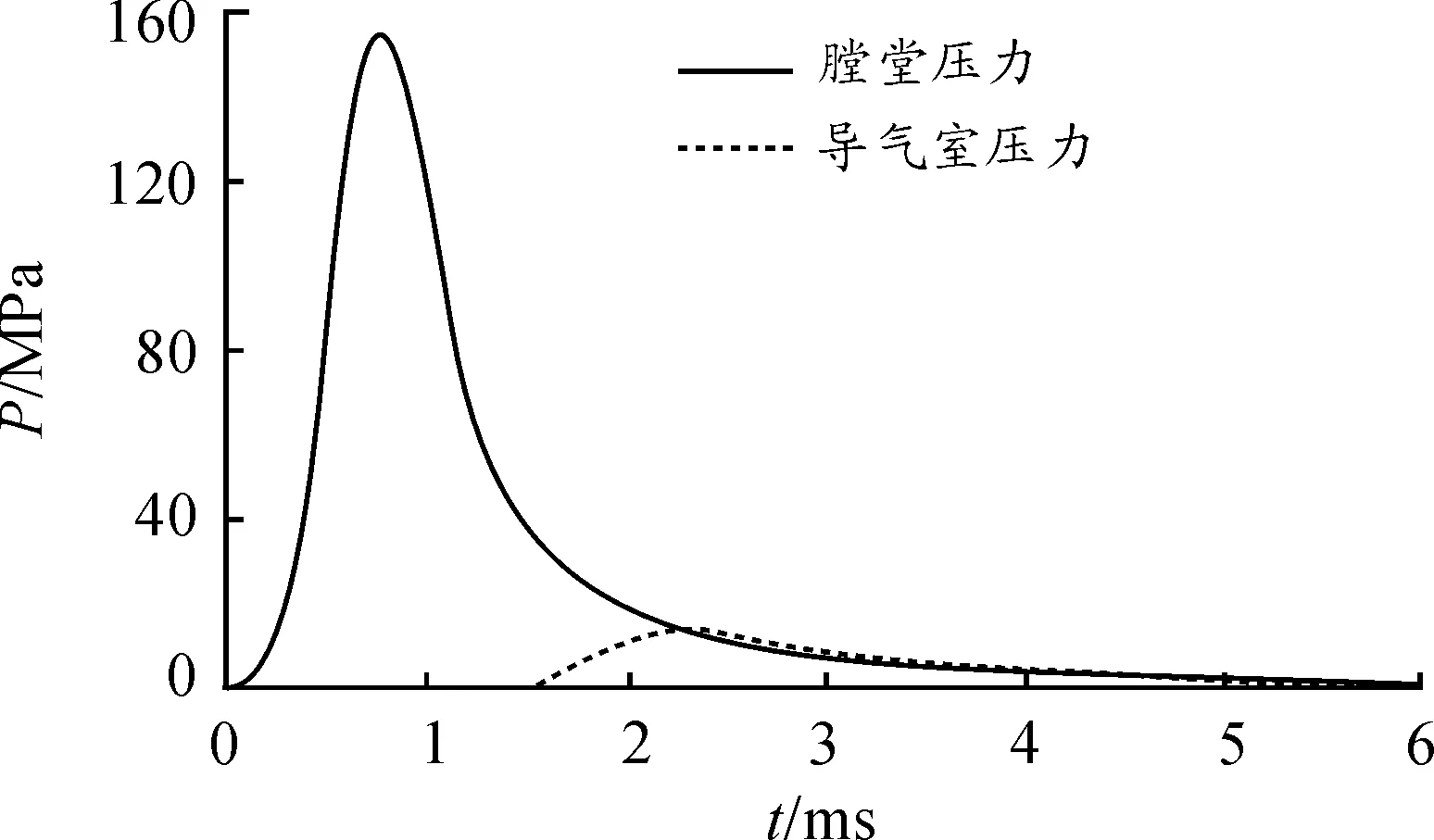
图2 内弹道及后效期计算曲线

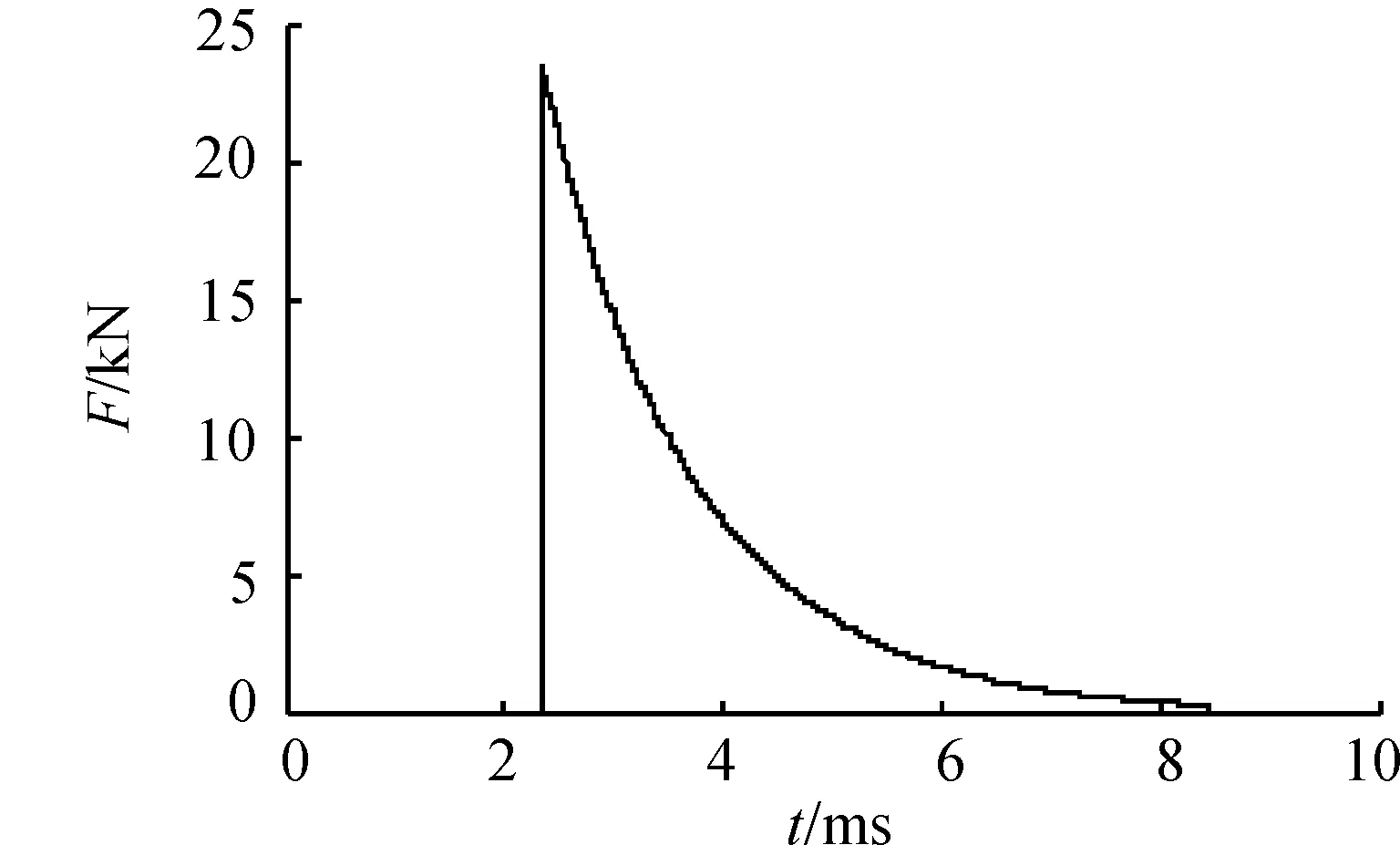
图3 膛口制退力计算曲线

图4 弹丸速度曲线

由图2～图4可以看出，在初始时刻榴弹击发，膛压开始急剧增大；在0.34 ms时膛压升高到30 MPa，榴弹开始加速运动；在0.78 ms时膛压最大上升到了155.5 MPa然后开始迅速下降；在1.5 ms时榴弹通过导气孔，导气室压力开始迅速增加并在2.24 ms时最大为14.1 MPa；在2.34 ms时弹丸出膛口，弹丸速度达到602 m·s-1,此时膛口制退力开始急剧上升到23.6KN后开始逐渐下降。在2.34 ms以后进入后效期作用阶段，弹丸在剩余气体压力的作用下继续加速运动一段时间在2.4 ms时最终增加到最大速度610 m·s-1。

抽壳阻力与拨弹阻力以外力的形式作用于模型，可由以下公式近似求得[9]。抽壳阻力计算方程为

(1)

式中：f为弹壳与膛壁的摩擦因数；l为弹壳长度；δ为弹壳厚度；α为弹壳半锥角；p为膛压；DPN为弹壳平均内径；DPW为弹壳平均外径；E为弹壳弹性模量；u为弹壳后退行程；Δ0为弹壳初始相对紧缩量。

拨弹阻力计算方程为

(2)

式中：F0为拨弹阻力；N0为脱弹板对榴弹的支撑反力；Qx、Qy分别为弹链对弹体的面接触力在水平和垂直方向的投影，可通过有限元模型求解；α0为弹体与脱弹板接触面法向量与垂直方向夹角。

2.2 模型构建

本研究建立该减后坐方案榴弹发射器刚柔耦合动力学模型的步骤如下：枪管及脚架作为柔性体考虑，以准确模拟射击时的实际情况，确保下一步枪管振动分析结果的准确性[10-11]，将枪管及脚架组件分别在ANSYS中进行有限元计算，取前20阶模态生成的柔性体文件导入ADAMS计算模型中；依据各部件之间的运动关系，该减后坐方案榴弹发射器的各刚体之间以运动副连接；创建的柔性体以MARKER点与相应刚体部件固定；对各部件之间定义碰撞关系；将本文2.1节中计算所得的各减后坐方案榴弹发射器的载荷施加于对应部件上，通过建立传感器的方式实现各载荷的作用时机符合实际射击过程。所建立前冲击发减后坐方案榴弹发射器的模型如图5所示。

图5 减后坐动力学模型

2.3 模型分析

由于该采用前冲击发减后坐方案的榴弹发射器弹丸初速达到600 m·s-1以上，尚处于研究阶段，本研究通过建立该减后坐方案榴弹发射器刚柔耦合动力学模型，利用ADAMS进行仿真，获得了首发射击时的机框运动特征量。利用高速摄影法[12]，测量了传统导气式榴弹发射器的机框运动特征量，如图6所示。

图6 机框位移时间曲线

通过对比传统导气式实验值与减后坐方案仿真值，发现二者在射击过程中前期基本一致，但是在0.135 s时传统导气式实验值在火药燃气作用下开始上升时，减后坐方案仿真值继续下降，直到0.142 s时减后坐方案仿真值才开始上升，导致二者曲线差异越发明显。这是由于减后坐方案榴弹发射器具有前冲击发结构，机框、机头与枪管会继续前冲，并在前冲速度最大时火药燃气才开始作用，导致减后坐方案仿真值曲线上升时间滞后，与实际情况相符。整体来看，二者机框位移与机框速度曲线变化趋势基本相同，说明所建立的采用前冲击发减后武器系统动力学模型是比较可信的。

3 前冲击发对系统枪管振动的影响

3.1 连发射击振动分析

利用ADAMS对已建立的减后坐方案发射动力学模型进行仿真，获得了前5发连发射击过程中枪管前冲及后坐的运动特征量曲线和膛口跳动曲线，如图7～图14所示。坐标系方向选取在图1与图5中均已经标出。

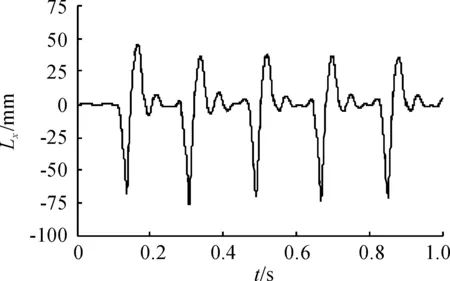
图7 连发过程中枪管前冲及后坐位移时间曲线

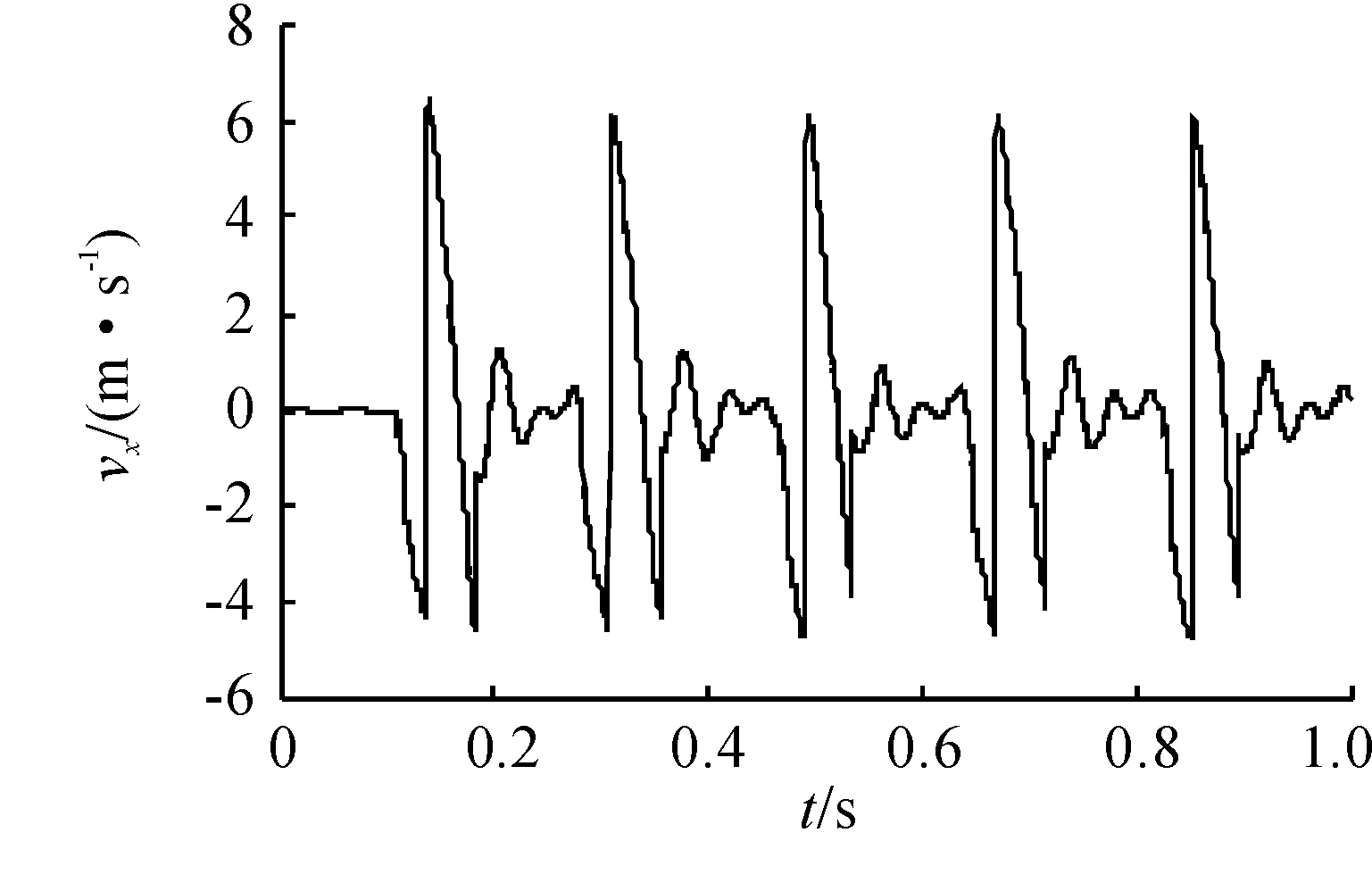
图8 连发过程中枪管前冲及后坐速度时间曲线

从图7可知，首发射击时由于射击状态未达到稳定，其前冲行程比其他4发明显要大很多。在连发射击状态平稳时，武器系统完成4连发的完整时间为0.715 s，则武器理论射速为335 r/min(5.6 Hz)。在武器射击过程中，枪管浮动前冲行程为73 mm，后坐位移为109 mm。由图8可以看出，在连发射击过程中，武器系统最大前冲速度为4.64 m·s-1,最大后坐速度为6.1 m·s-1。

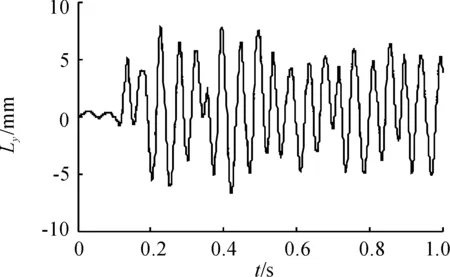
图9 连发过程中膛口高低振动位移时间曲线

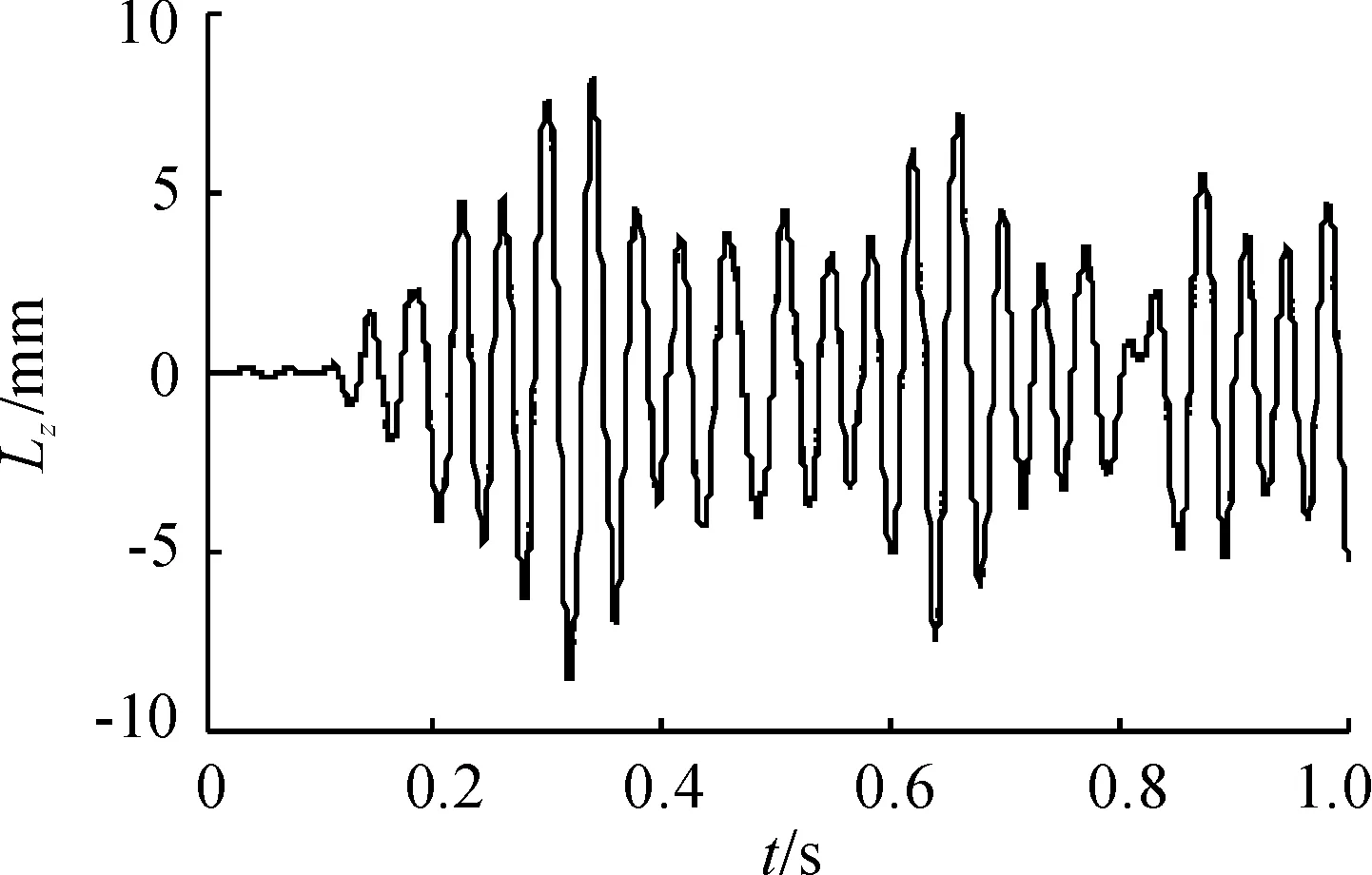
图10 连发过程中膛口方位振动位移时间曲线

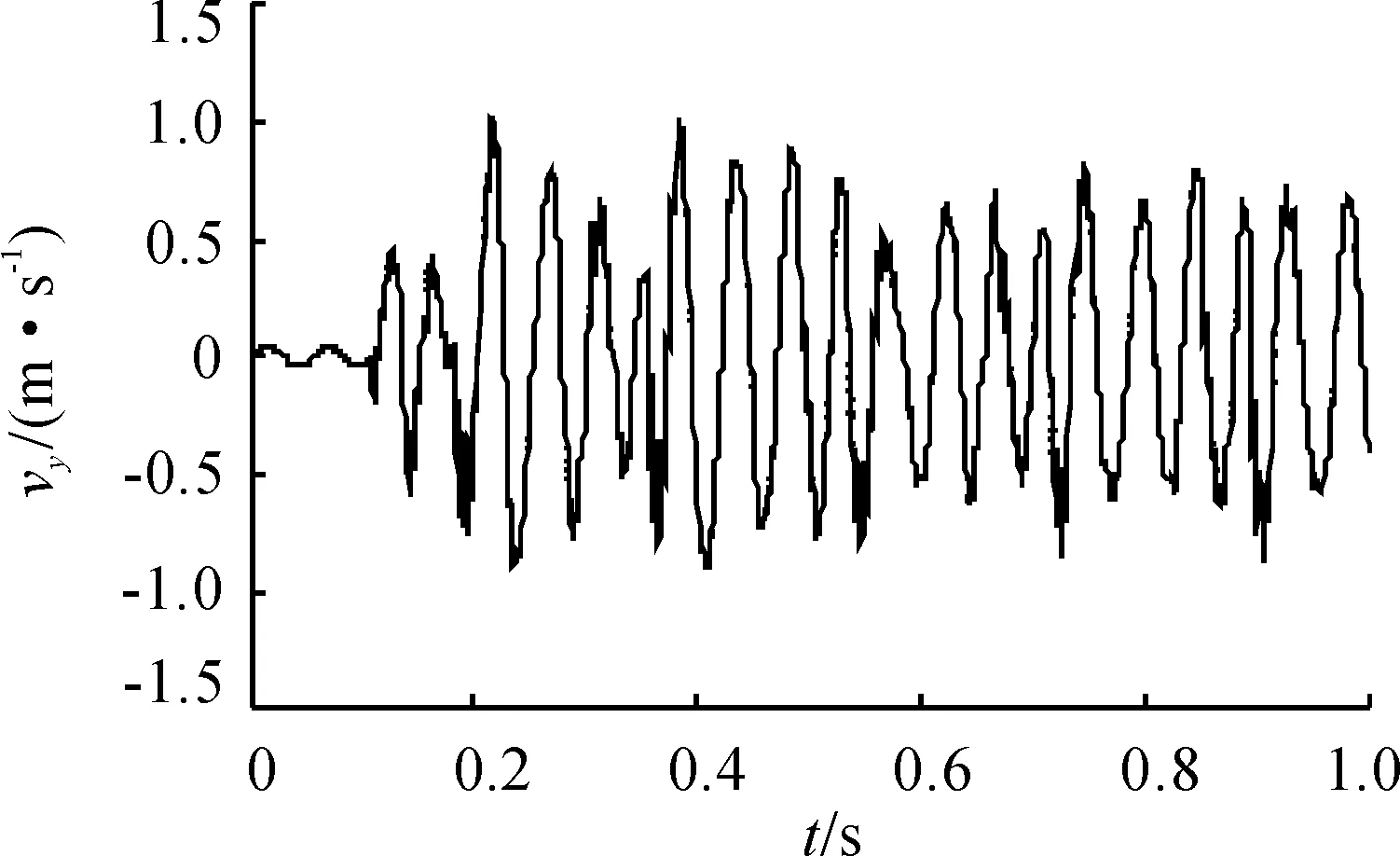
图11 连发过程中膛口高低振动线速度时间曲线

图12 连发过程中膛口方位振动线速度时间曲线

图13 连发过程中膛口高低振动角位移时间曲线

图14 连发过程中膛口方位振动角位移时间曲线

根据图9～图14，可以获得减后坐高初速榴弹发射器膛口运动特征量的最大幅值，如表4所示。

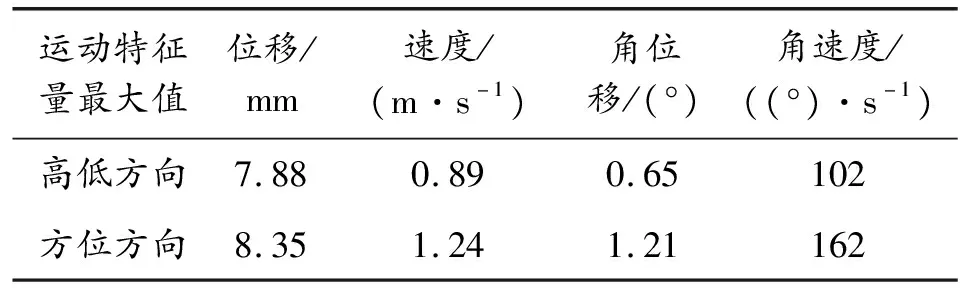
表4 膛口运动特征量的最大幅值

从图9～图14及表4可以看出，射击过程中，膛口在高低方向上振动的位移极值和速度极值发生在弹丸击发时及机框后坐到位撞击缓冲杠杆时，在方位方向上振动的位移极值和速度极值发生在机框复进与枪管撞击结合时及后坐拨弹时，速度峰值产生得略早。发现膛口跳动在方位方向上比高低方向上略明显，这是因为机框在继续前冲推开枪管锁扣及与枪管碰撞结合时会导致枪管在方位方向上波动增大；另一方面，在后坐过程中，机框在后坐拨弹时也造成了枪管在方位方向上的波动。

3.2 前冲击发对武器系统射击密集度的影响分析

3.2.1射击密集度计算公式

表征身管振动的数据结果繁多复杂[13]。需要更加简洁明了地分析不同浮动装置结构参数的影响。对各项膛口跳动数据进行处理可获得射击密集度[14]。以武器静平衡状态下膛口位置为原点，坐标系与动力学建模一致，弹丸质心运动方程组为：

(3)

式中：v为弹丸速度；u为v在x轴上投影速度；v1为v在z轴上投影速度；v2为v在y轴上投影速度；C为弹道系数；H(y)为空气密度函数；G(v)为阻力函数；S为弹丸飞行距离。

外弹道初始条件为：

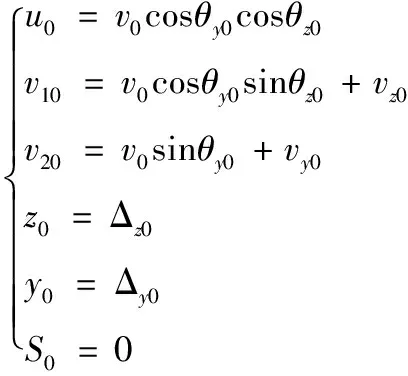
(4)

式中：v0为弹丸初速；θz0、vzo、Δz0与θzo、vy0、Δy0分别表示弹丸出膛口瞬间在方位方向上与高低方向的起始射角扰动、起始速度扰动、起始位移扰动。

由式(4)计算可得各发弹在100 m处弹着点坐标，则以密位表示的立靶密集度为：

(5)

式中：Ez、Ey分别表示在方位以及高低方向上的射击密集度情况。

3.2.2不同结构参数下计算结果分析

分析前冲击发结构参数对身管振动的影响，是为了进一步确定其产生的膛口跳动对射击精度的影响规律，研究各前冲击发结构参数下的射击密集度能直观反映各参数的优劣。为了保证减后坐高初速榴弹发射器在2 000 m的有效射程上仍具有较好的命中率，必须满足Ez≤1 mil，Ey≤1.6 mil。如图15～图17所示，下文的计算结果均在除某一项浮动装置结构参数不同外，其他射击条件一致的情况下进行5连发射击仿真所得。

由图15～图17可以看出，符合高精度指标的前冲行程为94 mm到105 mm，前冲簧预压力为1 180 N到1 340 N，前冲簧刚度为3.5 N·mm-1到5.2 N·mm-1。发现在初始的计算条件下EZ=0.95 mil而Ey=1.4 mil,前文的振动情况分析得出膛口跳动在方位方向上略明显，而射击密集度的计算结果表明在方位方向上射击精度反而更好，说明其受膛口初始扰动的影响大过受身管总体振动情况的影响。适当地调节前冲击发结构的参数取值以达到有效改善射击精度的方法是可行的。总体来看，前冲行程越短，前冲簧预压力越小，则前冲击发过程中抵消的后坐冲量越少，导致后坐冲量过大加剧了后坐到位时的碰撞幅度，弹丸出膛口时波动变大造成射击精度变差；前冲簧刚度越大，则前冲击发机构作用时越不平缓，系统稳定性下降，不利于射击精度；而前冲行程过长、前冲簧预压力过大或者前冲簧刚度过小可能会导致系统无法后坐到位，反而导致射击精度下降。

图15 武器射击密集度在不同前冲行程下的变化趋势

图16 武器射击密集度在不同前冲簧预压力下的变化趋势

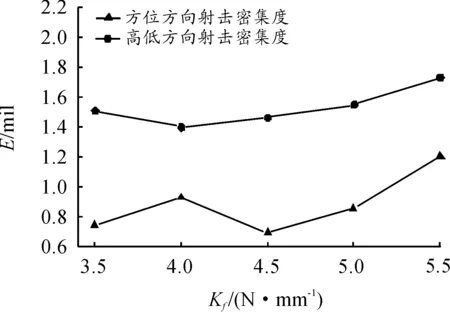
图17 武器射击密集度在不同前冲簧刚度下的变化趋势

4 结论

提出了一种前冲击发方式的新型高初速低后坐榴弹发射器减后坐方案，通过仿真分析，确认了研制初速高、射频高、射程远、精度高以及后坐力低的自动榴弹发射器在理论上是可行的。通过编程计算内弹道和后效期过程，获得了前冲击发方式的新型高初速低后坐榴弹发射器的内弹道曲线及导气室曲线规律。通过对减后坐方案榴弹发射器进行仿真分析，获得了自动机的运动特征量曲线，可以自动完成5连发射击过程，除首发射击外其余射击过程均比较平稳。分析了前冲击发对身管振动的影响规律，发现膛口跳动在方位方向上略明显。通过射击密集度计算获得了各前冲击发结构参数下的射击密集度变化趋势，确定了在高精度射击指标下前冲击发结构的各参数取值范围以及各参数对射击精度的影响规律，发现各参数调试范围过大或者过小都会导致射击精度降低，适当地调节前冲击发结构的参数取值以达到有效改善射击精度的方法是可行的。后续的工作将围绕对新型高初速低后坐榴弹发射器的进一步优化设计以获取最优的前冲击发结构参数以及加工出减后坐方案实验样枪进行实验验证展开研究。