基于椭圆概率误差的落点精度评定方法

魏宗康，高荣荣，周 姣，江 麒

基于椭圆概率误差的落点精度评定方法

魏宗康，高荣荣，周 姣，江 麒

（北京航天控制仪器研究所，北京，100854）

制导导弹和炮弹的命中精度是衡量弹道武器等系统性能的一项重要评价指标，其中圆概率误差（Circular Error Probable，CEP）是最常用的落点精度评定方法。由于导航系统的偏差和其他随机因素的影响，实际导弹的落点分布通常沿不同方向不均匀并且方向相关，传统的CEP无法描述落点误差的方向性和相关性。根据落点分布的相关性和非等标准误差特点，提出了一种新的椭圆概率误差（Elliptic Error Probable，EEP）的落点精度评定方法，并给出了精确表达式。该方法利用椭圆的长轴、短轴和旋转角度3个参数描述落点精度，分别建立了沿原始坐标轴的两参数椭圆概率误差模型和沿标准差解耦坐标轴的三参数椭圆概率误差模型。通过仿真对比发现，相比圆概率误差和两参数椭圆概率误差，三参数椭圆概率误差模型面积最小。因此，椭圆概率误差能够更精准地描述导航精度在不同方向的差异及方向相关性，将为预估落点误差的方向性及目标摧毁概率范围提供依据。

落点精度分析；椭圆概率误差；相关性；方向性；非等标准误差

0 引 言

导弹和炮弹等的命中精度是评价导弹和惯导系统实际作战能力的主要性能指标和评估武器系统稳定性的基础手段。精确的落点精度估计为导弹性能和惯性导航技术的改进以及实际作战中的目标摧毁概率估计提供非常重要的指导依据。

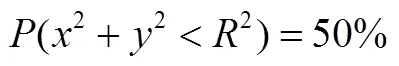
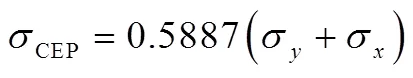
两种情况加权求和的形式，例如《制导火箭弹射击精度评估方法》中[3]中采用的：

以及多种情况加权求和的形式[4]及其它更精确的分段近似计算方法[5]。例如在文献[4]中给出的：

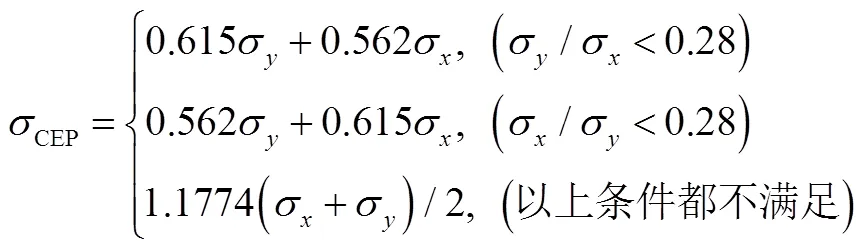
另外，在文献[6]中从统计学角度认为CEP非定值，而是在一个置信度区间。

在这种情况下，虽然传统的CEP精度评定方法在一定程度上能够描述落点分布的密集程度，但CEP对落点精度的评定存在明显不足。首先，由经验公式得到的 CEP没有准确表达式，并且不同表达形式下的结果不一致，造成落点精度评定不准确；其次，采用CEP评定落点精度的核心是将两维分布折合到一维分布，仅通过一个参数表示精度，这样将造成落点分布方向差异信息缺失；再次，由于导航系统误差，实际的导弹落点分布通常存在方向相关性，CEP无法表征落点不同方向的相关性。

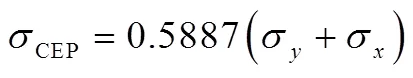
针对CEP描述精度存在评估方式模糊、无精确表达式、方位信息缺失以及方向相关性差异不明显等缺点，本文提出一种相关性的基于椭圆概率误差描述落点精度的方法，并给出了精确表达式。椭圆概率误差模型由于具有两个半轴，因此可以表达出多于圆的分布特性，同时，椭圆绕中心点旋转后长短半轴的方向信息也可以用来表达落点更加精准的分布特性。

图1 用CEP表征落点精度的示意

1 标准差不相关且均值为零时的椭圆概率误差

在公开文献中，为了避免复杂计算，均假设落点分布沿两个方向不相关，不考虑方向相关对落点精度的影响。因此，本文首先提出在落点分布标准差不相关时基于椭圆概率误差（Elliptic Error Probable，EEP）的落点精度评定方法。相比CEP落点精度指标，该方法能准确描述落点分布沿不同方向密集度的差异[7]。

与圆概率误差的定义相似，椭圆概率误差定义为落点位置落入以目标点为圆心的面积最小的椭圆内的概率为50%时，该椭圆沿垂直轴的半径（R，R）称为椭圆概率误差。

当两个方向落点位置误差的标准差不相关时，假设落点的均值为零，其可用公式表达为

求解概率方程式（1）可以得到：

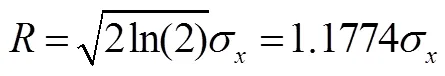
则，椭圆的两个半径为

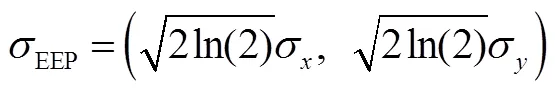
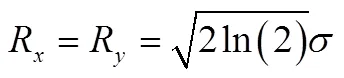
图2 标准差不相关时两参数椭圆概率误差与圆概率误差模型对比

由椭圆概率误差可以看出，沿轴方向导弹有50%的概率落在117.74 m以内，而沿轴方向导弹偏离中心的距离相对更远，有50%概率落在470.96 m的范围内，导弹落点在轴方向比轴方向更为准确密集。对比圆概率误差，椭圆概率误差可以更准确地描述落点分布的方向性和密集度。

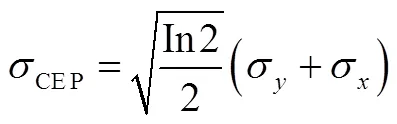
2 标准差相关且均值为零时的两参数椭圆概率误差

由于导航系统的偏差和其他随机因素的影响，实际导弹的落点分布通常存在方向相关性，即轴和轴方向落点分布不独立，这将导致导弹落点密集的方向不沿轴和轴方向，而是与轴和轴存在一定夹角。将第1节中标准差不相关时的椭圆概率误差的计算方法引申到标准差相关时的情况，使用椭圆的长、短轴评定导弹的落点精度。

按照椭圆概率误差的定义，采用半径分别与、轴重合的椭圆，列出落点分布的概率方程：

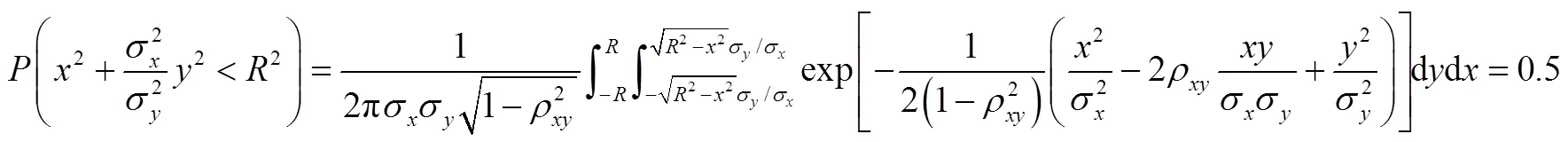
求解可以得到：

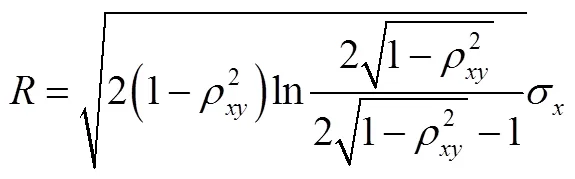
则，椭圆的两个半径分别为

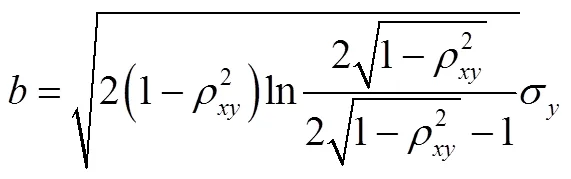
根据椭圆面积表达式，带入椭圆半径式（6）、式（7），可以得到椭圆的面积为

图3 标准差相关时两参数椭圆概率误差模型

该椭圆包含了50%的落点概率，在横轴和纵轴方向一定程度上体现了导弹落点分布的方向性，但是落点分布的相关性并没有准确地体现出来，并且此椭圆的面积并非最小。因此，需要寻求一种既能准确表达落点分布方向性和相关性的椭圆，同时又要求此椭圆的面积达到最小，以此来更加精准地表达落点精度。

3 标准差相关且均值为零时的三参数椭圆概率误差

在标准差相关的两参数椭圆概率误差基础上，提出了三参数概率误差模型。当落点位置分布标准差相关时，在坐标系中存在一组坐标变换，使该组数据标准差变换到坐标系中时相互独立[8,9]。将坐标系旋转一个角，坐标变换表达为

为了使变换后的坐标系下，落点位置分布标准差相互独立，则取：

式（10）的物理意义也可描述为，平面中一个固定的椭圆在和坐标系中的表达式分别为

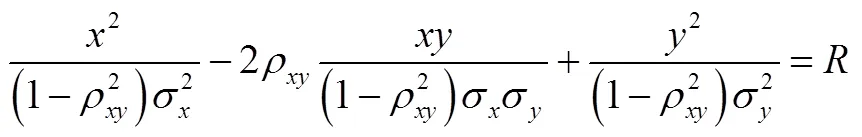
经过坐标变换后，在坐标系中独立方差为

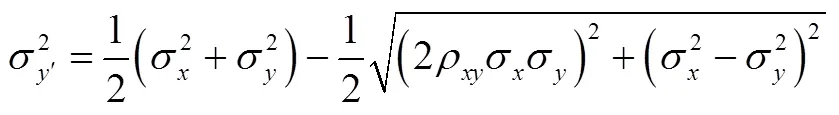
因为在两个坐标系下表示为同一个椭圆，因此，在坐标系中落点分布的概率方程与坐标系中的概率方程相同。

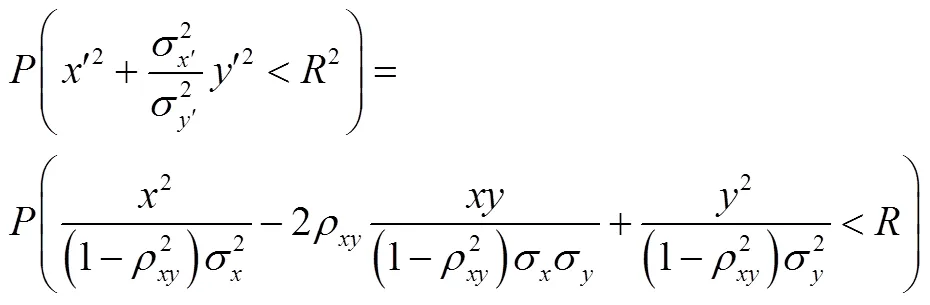
最后，将椭圆从坐标系中变换到坐标系中，变换公式为

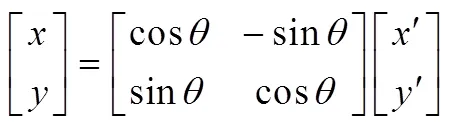
在坐标系中的椭圆方程为

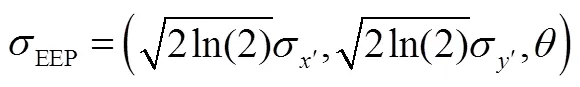
根据椭圆的面积公式，可以得到该椭圆的面积为

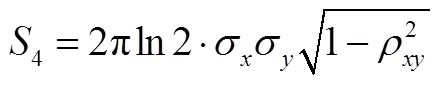
以某型号导弹落点仿真为例说明三参数椭圆概率误差的求解。参数与第2小节相同，模拟打靶1000次，忽略系统误差，X轴和Y轴方向标准差分别为sx=100 m、sy=400 m，相关系数=0.5，落点分布如图4所示。由式（10）可以得到旋转角度q=82.5343°。经过坐标旋转后，在坐标系OX¢Y¢中落点X轴和Y轴方向标准差（式（13）、式（14））分别为sx’=403.2628 m和sy’=85.9018 m。在旋转后的OX¢Y¢坐标系中，椭圆概率误差=（403.2628m，85.9018m）（式（16））如图4中实线所示。由OX¢Y¢坐标系中的椭圆可知，旋转后的椭圆，解决了落点分布相关性的问题，准确的表示了落点误差精度。

最后，将椭圆还原到原始坐标系中，得到原始坐标系下的落点分布以及椭圆概率误差模型，如图5所示。由图5中可看出，沿椭圆的长轴和短轴，概率为50%的落点位置分别在短轴为85.9018 m、长轴为403.2628 m的椭圆以内；椭圆旋转方向为82.5343°，即在82.5343°方向上落点分布密集度最低，随机误差相对较大。经过旋转的椭圆概率误差模型，不仅可以描述落点分布沿两个轴分布的不均匀性，也可以描述落点分布的相关性。

图5 三参数椭圆概率误差模型

4 对比分析

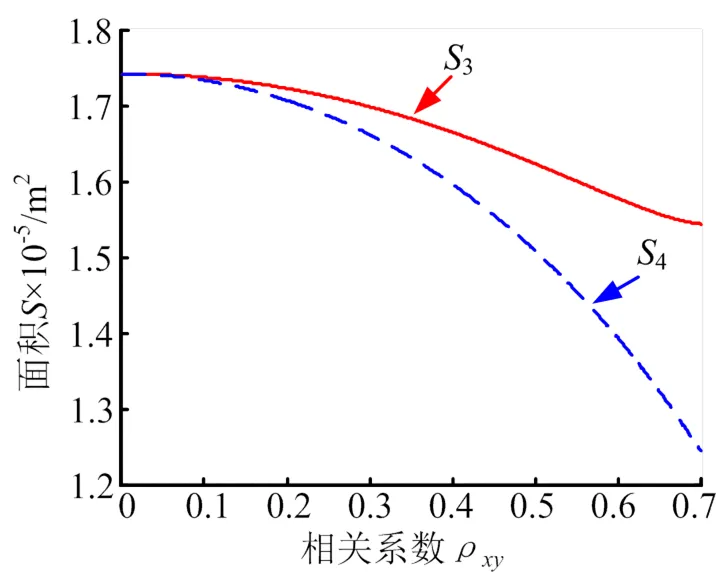
图6 两参数和三参数椭圆概率误差模型面积对比

注：实线3为两参数椭圆概率误差计算的面积；虚线4为三参数椭圆概率误差计算的面积

在进行导弹精度试验中，导弹向目标点重复打击时，落点的散布受内部和外界很多随机因素影响，而这些干扰因素互相之间不独立。因此，采用三参数椭圆概率误差EEP落点精度评定方法，首先，可以判定落点在不同方向上的差异性，椭圆的长轴与短轴比越大，说明在长轴方向上的落点密集度越低，随机误差也就越大，因此可根据落点在两个不同方向上的密集度来确定相应方向上的落点随机误差的大小；其次，由于实际落点分布的相关性，误差椭圆的长轴与地理北向或东向的夹角十分重要，此角度关系到落点密集度判定的准确性以及最终椭圆概率误差的面积范围；最后，三参数椭圆概率误差方法所得椭圆面积明显小于不考虑相关性的椭圆概率误差下的面积，而在落点精度评定中，一般认为圆或椭圆面积越小，则导弹打击精度越高，且对摧毁目标的范围估计精度就会越高、越精确，打击成功的概率就会越高。因此，在进行型号导弹精度评估中，三参数椭圆概率误差评定方法相较于CEP和不考虑相关性的椭圆概率误差方法，能增加对导弹落点精度评估的准确性。

5 结 论

本文针对传统的圆概率误差描述两维落点精度存在评估方式模糊、无精确表达式、方位信息缺失以及方向相关性差异不明显等问题，提出了一种新的三参数椭圆概率误差的落点精度评定方法。该方法在平面内以覆盖了50%落点的椭圆表征落点位置误差分布，其中，椭圆的长轴、短轴分别描述落点分布沿两个轴概率的差别，旋转角度描述了椭圆在平面内所处的方位。该方法能够更准确地描述导航精度在不同方向的差异及方向相关性，为评价现有制导导弹和炮弹的命中精度提供了良好的参考价值，并为分析误差产生原因提供依据。

[1] 张乐, 李武周, 巨养锋, 等. 基于圆概率误差的定位精度评定方法[J]. 指挥控制与仿真, 2013, 35(1): 111-114.

Zhang Le, Li Wuzhou, Ju Yangfeng, et al. Positioning accuracy evaluation method based on CEP[J]. Command Control & Simulation, 2013, 35(1): 111-114.

[2] 梁健. 目标定位精度评估方法研究[J]. 无线电工程, 2015, 45(4): 65-69.

Liang Jian. Research on evaluation approach of target positioning accuracy[J]. Journal of Radio Engineering, 2015, 45(4): 65-69.

[3] 周海玲，王军林，郑宁歌，等. 制导火箭弹射击精度评估方法[J]. 测试技术学报, 2014, 28(2): 98-102.

Zhou Hailing, Wang Junlin, Zheng Ningge, et al. Evaluation method of guided rocket of shooting accuracy[J]. Journal of Test and Measurement Technology, 2014, 28(2): 98-102.

[4] 王艳永, 贾兴荣, 高晖, 等. 基于统计推断的惯性定位精度评估方法对比[J]. 计算机应用, 2012, 32(S2): 276-279.

Wang Yanyong, Jia Xingrong, Gao Hui, et al. Comparison of inertial positioning accuracy evaluation approach based on statistical inference[J]. Journal of Computer Application, 2012, 32(S2): 276-279.

[5] 冀大雄, 刘健. 水下机器人圆概率偏差的有效预报[J]. 计算机应用, 2012, 32(10): 2960-2962.

Ji Daxiong, Liu Jian. Effective forecast of circular error probability in underwater robots[J]. Journal of Computer Application, 2012, 32(10): 2960-2962.

[6] 郑小兵, 董景新, 张志国, 等. 基于蒙特卡罗法的弹道导弹落点密集度验前估计[J]. 中国惯性技术学报, 2011, 19(1): 116-121.

Zheng Xiaobing, Dong Jingxin, Zhang Zhiguo, et al. Mente Carlo evaluation for fall point dispersion of ballistic missile based on prior information[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 116-121.

[7] 刘畅, 刘湘伟, 郭建蓬, 等. 基于卡尔曼滤波的无人机测向定位算法研究[J]. 舰船电子对抗, 2013, 36(1): 21-25.

Liu Chang, Liu Xiangwei, Guo Jianpeng, et al. Study of UAV DF location algorithm based on KF[J]. Shipboard Electronic Countermeasure, 2013, 36(1): 21-25.

[8] 艾佛里尔, 查特菲尔德B. 高精度惯性导航基础[M]. 北京: 国防工业出版社, 2002.

Eaveslille, Chatfield B. Fundamentals of high accuracy inertial navigation[M]. Beijing: National Defence Industry Press, 2002.

[9] 杨士英, 罗景青. 利用误差椭圆消除虚假定位的算法研究[J]. 电子对抗技术, 2004, 19(5): 3-7.

Yang Shiying, Luo Jingqing. Study on the erasing false-location algorithm by error-ellipse[J]. Electronic Countermeasure Technology, 2004, 19(5): 3-7.

An Accuracy Evaluation Method of Fall Points Based on Elliptic Error Probable

Wei Zong-kang, Gao Rong-rong, Zhou Jiao, Jiang Qi

(Beijing Institute of Aerospace Control Devices, Beijing, 100854）

The hit accuracy of ballistic missile is a critical accuracy evaluating index for weapon systems and circular Error Probable (CEP) is the most used accuracy evaluation method of fall points. In practice, the missile fall point distribution is usually in-homogeneous and related along different direction. In this reason, CEP cannot describe the directional difference and relativity of fall point error. Based on the related and non-equal standard error of fall point distribute, a new elliptic error probable (EEP) is proposed and its accurate expression is given. According to the new hit accuracy evaluation method, a two-parameter elliptic error probable along initial coordinate system and a three-parameter elliptic error probable along decoupled standard error coordinate system are built. Finally, the simulation shows that the three-parameter elliptic error probable has the smallest area, compared with the CEP and the two-parameter elliptic error probable. Consequently, three-parameter elliptic error probable can describe the directional difference and relativity of fall point error precisely, which will provide a basis for the estimation of fall point direction and the analysis of the error generation reasons.

falling point accuracy analysis; elliptic error probable; relativity; directionality; unequal standard error

U666.1

A

1004-7182(2020)02-0058-06

10.7654/j.issn.1004-7182.20200212

魏宗康（1973-），男，研究员，主要研究方向为导航制导与控制。

高荣荣（1994-），女，硕士研究生，主要研究方向为导航制导与控制。

周 姣（1988-），女，工程师，主要研究方向为导航制导与控制。

江 麒（1993-），男，助理工程师，主要研究方向为导航制导与控制。

2018-06-13；

2018-09-20