惯性/星光制导误差分离的可观测度研究
2020-04-22郭振西闵昌万
郭振西,武 斌,谢 佳,闵昌万
惯性/星光制导误差分离的可观测度研究
郭振西,武 斌,谢 佳,闵昌万
(空间物理重点实验室,北京,100076)
基于捷联惯性测量组合和星敏感器的“惯性+星光”复合导航方式综合了两种导航方式的优点,可以实现组合导航的高动态和高精度。研究了惯性/星光组合制导捷联安装的系统误差模型及其可观测度分析方法,计算了在不同位置进行误差分离的系统状态可观测度,并通过数学仿真证明了该分析方法的有效性,可应用于惯性/星光制导方案在线分离惯性失准角和安装误差角的方案快速论证。
捷联星光制导;误差分离;可观测度
0 引 言
“惯性+星光”复合导航方式取两种导航方式的优点而互补其短,既利用惯性器件全程自主地提供姿态信息,又利用星光在中段对惯性导航的误差进行修正,达到精确导航的目的[1]。为克服系统运动模型的非线性,现代捷联惯性/星光制导多采用扩展卡尔曼滤波(Extended Kalman Filter,EKF)、无损卡尔曼滤波(Unscented Kalman Filter,UKF)、粒子滤波(Particle Filter,PF)等滤波方法进行组合导航[2~8]。一般而言,对于机动发射平台而言,受载机运动和机体变形的影响,子惯导的初始失准角特别是方位失准角误差较大。为了保证自主制导的精度,可在飞行过程中采用“惯性+星光”的模式对初始方位失准角进行修正。有些飞行器受到安装空间的限制,星敏和惯组不能安装在同一个刚性支架上。受运输环境和飞行过程的影响,在观星时刻,星敏和惯组会产生一定的安装角误差,本文通过分析星敏和惯组之间的输出信息和误差激励模型,通过飞行器在观星时刻的简单滚转,在线分离安装误差,修正惯性导航系统的方位失准角。利用观测矩阵的奇异值分解计算分析不同误差状态的可观测度,为飞行过程的姿态角激励时序提供依据,最终保证惯性自主制导系统的误差修正精度。
1 惯性导航和星敏感器建模
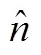
1.1 双视场星敏误差模型
双视场星敏感器一次观星可以测得惯性系的基准。对于与飞行器捷联安装而言,确定惯性基准的具体方法如下(星敏感坐标系和飞行器坐标系重合):
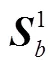
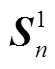


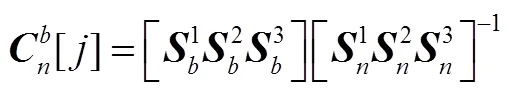
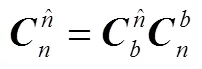
1.2 惯组误差模型
惯性星光组合制导主要包括两个误差源:计算惯性系误差(导航系误差)和星敏感器安装误差。对于采用高精度惯导系统的“惯组+星光”组合制导系统,将不同观星时刻的陀螺漂移和星敏观星误差看作噪声。
a)定义导航系误差:
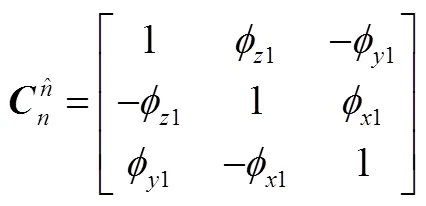
b)星敏感器安装误差:
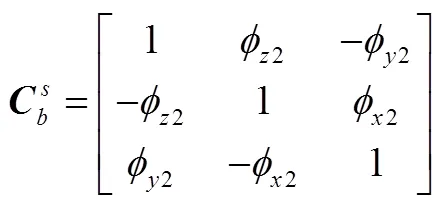
c)第次观星的结果:

式(6)中,将方向余弦矩阵替换为对应的四元数算法[7]:
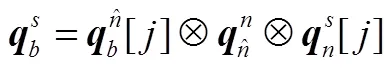
由式(4)~(7)得:
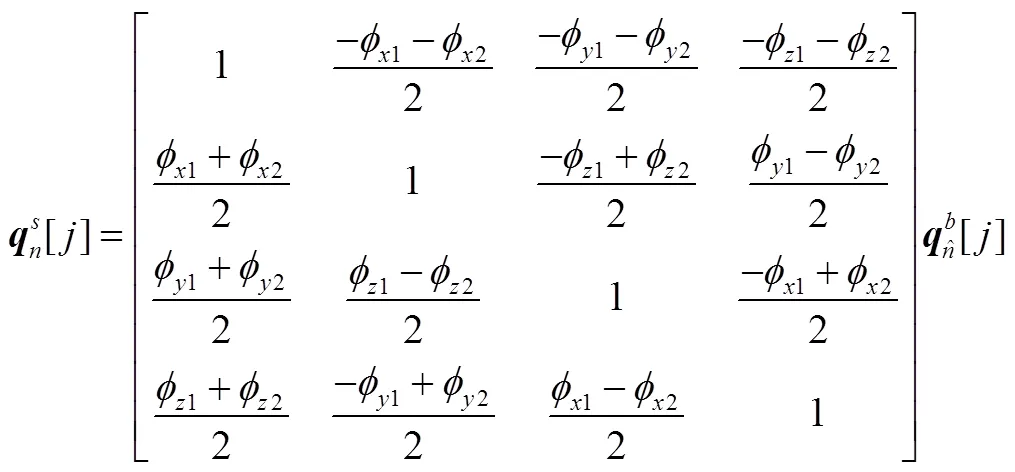
写成矩阵形式:

式中

式(9)即一次观星所得到的观测量和系统状态之间的关系。
2 星光制导的系统可观测度
根据式(9)如果有多次观测则可以列出一个方程组为
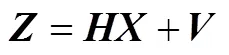
得到的最小二乘观测结果和协方差矩阵为[8]
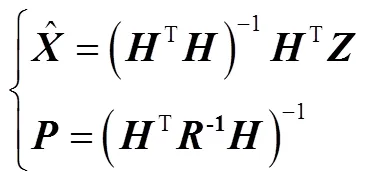
式中为星敏测量结果;为待估计的失准角;为观测矩阵;为星敏感器观测四元数的噪声方差;且

如果通过阵的特征值判断失准角估计结果受调姿矩阵的影响,则阵特征值反映了失准角估计误差的协方差。
如果系统的可观测度足够大,即阵不奇异,可以通过最小二乘法分离出6个误差项,即3个星敏安装误差角和3个惯组失准角。计算不同状态下的矩阵的奇异值和其所对应的奇异值分解向量,可以反映不同观星方式下的系统可观测度。本文采用系统观测矩阵的最小非0奇异值表征可观测状态的可观测度。
2.1 一次观星可观测度
对双视场星敏一次观星的观测矩阵进行奇异值分解:
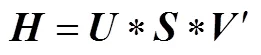
得到:

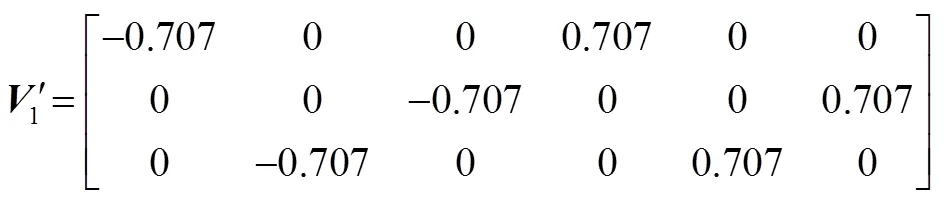
2.2 两次观星可观测度
星敏两次观星,分别绕惯性系旋转角度为30°、45°、60°,得到:
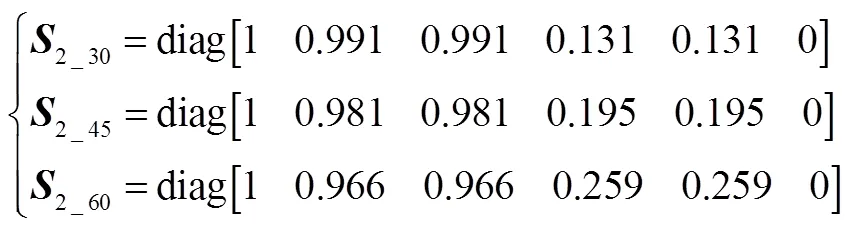

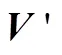
2.3 三次观星的可观测度
星敏3次观星,分别绕惯性系和旋转30°,得到:
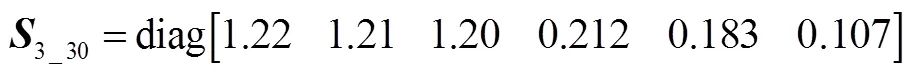
矩阵的秩为6,无0奇异值,所有状态可观,全部失准角和安装误差角可分离。不同观星状态下观测矩阵的可观测度如表1所示。
表1 不同观星情况下的观测矩阵的可观测度
Tab.1 System Observability under Different Stargazing Conditions
观星情况1次观星*2次观星(绕惯性系X轴旋转)3次观星 观星状态不旋转旋转30°旋转45°旋转60°分别绕X、Y旋转30° H矩阵秩356 奇异值最小值10.1310.1950.2590.107 系统可观测状态√×××√ √√√√√ √√√√√ ××××√ ×√√√√ ×√√√√
注:*一次观星的可观测状态,是指没有安装误差角时,3个失准角可观
根据上面的分析,可以得到以下结论:
a)在没有安装误差的情况下,一次观星可以测得三轴失准角;
b)两次观星总有一个方向的安装误差角和失准角不可观,即所绕轴的失准角和安装误差角不可观,而与转动方向垂直的安装误差角和方位失准角可分离。
c)两次观星绕一个轴的转动角度越大,系统的可观测度越大。
d)两次不同轴(惯性空间不同轴)转动可以测得全部3个失准角,并分离3个方向的安装误差角。
3 误差分离数学仿真
星敏感器两次测星所需的飞行器姿态(可根据需求,如尽可能调姿较小,优先使用滚转角等),生成星光调姿诸元进行装订。根据两次测星识别结果,分离星敏感器与惯组安装误差,同时修正飞行器方位向失准角,完成星光制导。取星敏感器测量误差为2"(1),惯组陀螺漂移2"(1),进行1000次打靶仿真,滚转方向两次测星的角度为30°,得到仿真结果如图1所示。
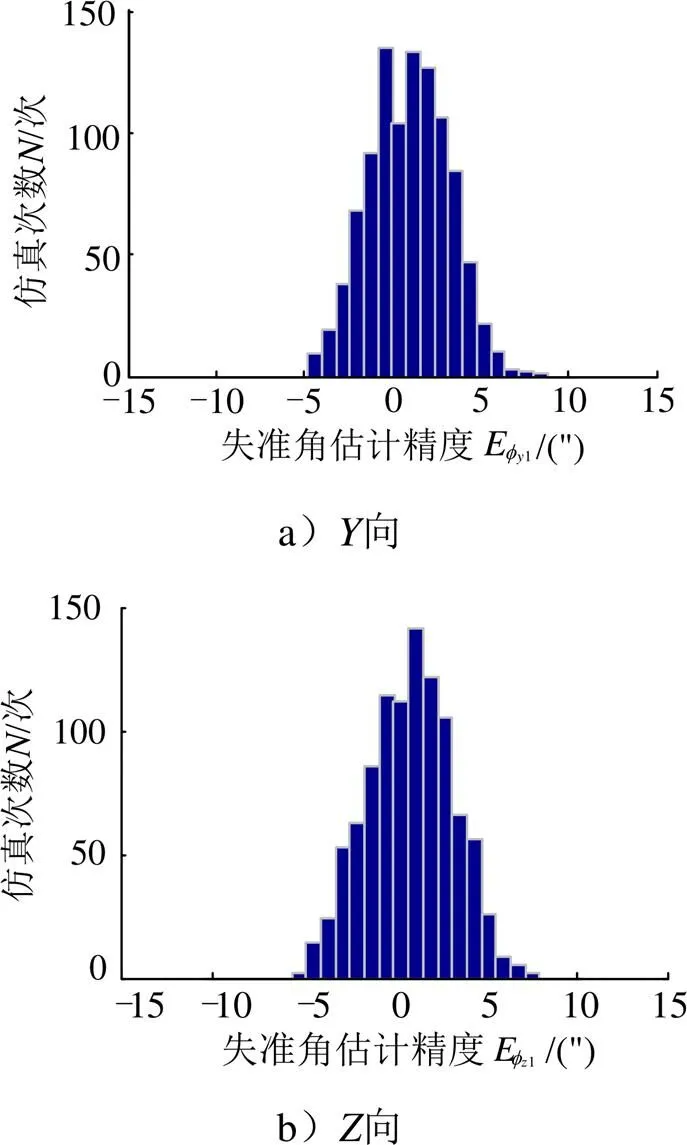
图1 绕X轴两次观星误差分离仿真结果
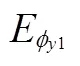
4 结 论
通过对“惯性+星光”复合制导的误差模型观测矩阵的奇异值分解,结合奇异值所对应的系统状态变量,可快速定量地计算出不同机动模式下的系统状态可观测度。结果表明:
a)两次观星总有一个方向的安装误差角和失准角不可观,即所绕轴的失准角和安装误差角不可观,而与转动方向垂直的安装误差角和方位失准角可分离。
b)两次观星绕一个轴的转动角度越大,系统的可观测度越大。
c)两次不同轴(惯性空间不同轴)转动可以测得全部3个失准角,并分离3个方向的安装误差角。
对于大视场星敏感器,在飞行器姿态角调整受限情况下,也可以参照这一结论制定相应误差分离调姿方案。
[1] 贾大玲, 李连仲, 严卫钢. 基于星敏感器的弹载陀螺工具误差分离研究[J]. 计算机仿真, 2002, 23(2): 40-43.
Jia Daling, Li Lianzhong, Yan Weigang. Missile borne gyroscope error separation based on star-sensor[J]. Computer Simulation, 2006, 23(2): 40-43.
[2] 赵长山, 秦永元, 夏家和. SINS/星敏感器组合导航方案研究[J]. 西北工业大学学报, 2008, 26(5): 631-634.
Zhao Changshan, Qin Yongyuan, Xia Jiahe. Improving online autonomous calibration of SINS/Star sensor integrated system[J]. Journal of Northwestern Polytechnical University, 2008, 26(5): 631-634.
[3] 敖宏奎, 等. INS/GNSS/CNS组合导航系统仿真研究[J]. 弹箭与制导学报, 2007, 27(4): 78-80.
Ao Hongkui, et al. Simulation of INS/GNSS/CNS integrated navigation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(4): 78-80.
[4] 罗楠, 许录平, 张华. 基于UKF和信息融合的航天器自主导航方法[J]. 中国空间科学技术, 2012, 4(2): 1-8.
Luo nan, Xu Luping Zhang Hua. Method of autonomous celestial navigation based on UKF and information fusion[J]. Chinese Space Science and Technology, 2012, 4(2): 1-8.
[5] Yin Jianjun, Zhang Jianqiu, Mike Klass. The marginalized rao-blackwellized particle filter for mixed linear/nonlinear state space models[J]. Chinese Journal of Aeronautics, 2007, 20(4): 346-352.
[6] 罗宁, 周磊, 张锐, 樊建文. 基于星敏感器的天文/惯导组合导航仿真研究[J]. 现代导航, 2014, 5: 342-346.
Luo Ning, Zhou Lei, Zhang Rui, Fan Jianwen. Research on CNS/SINS integrated navigation by simulation[J]. Modern Navigation, 2014(5): 342-346.
[7] 秦永元. 惯性导航[M]. 北京: 科学出版社, 2006.
Qin Yongyuan. Inertial Navigation System[M]. Beijing: Science Press, 2006: 288-292.
[8] 秦永元, 张洪钺, 汪淑华. 卡尔曼滤波和组合导航系统[M]. 西安: 西北工业大学出版社, 2015.
Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Theory of Kalman filter and integrated navigation system[M]. Xi’an: Northwestern Polytechnical University Press, 2015.
Study on the Observability of INS/CNS Guidance Error Separation
Guo Zhen-xi, Wu Bin, Xie Jia, Min Chang-wan
(Science and Technology on Space Physics Laboratory, Beijing, 100076)
The combined navigation system of INS (Inertial Navigation System)/CNS (Celestial Navigation System) is studied. The system error model of INS/CNS based on the strapdown INS installation approach is firstly developed. Then, the observability analysis method of the system error model is investigated, upon which the different observability of error separation at different locations is calculated. Finally, the effectiveness of the proposed analysis method is proved by numerical simulation. The above findings can be well applied to the inertial/starlight guidance scheme to quickly separate the inertial misalignment angle and the installation error angle, and finally achieve the high dynamics and precision.
strapdown starlight guidance; error separation; observability
V448
A
1004-7182(2020)02-0054-04
10.7654/j.issn.1004-7182.20200211
郭振西(1976-),男,研究员,主要研究方向为飞行器导航制导技术。
武 斌(1984-),女,高级工程师,主要研究方向为飞行器导航制导技术。
谢 佳(1985-),女,高级工程师,主要研究方向为飞行器导航制导技术。
闵昌万(1971-),男,研究员,主要研究方向为飞行器总体设计。
2018-10-31;
2019-02-21
