一种高精度在轨试验窗口设计方法研究

王 征

一种高精度在轨试验窗口设计方法研究

王 征

（中国运载火箭技术研究院，北京，100076）

在空间试验任务中，合理的试验窗口规划是保障飞行任务顺利开展的前提。考虑试验过程中的地面测控约束、可见光相机光照约束、太阳高度角极性约束及飞行器本体阳光反射角约束，建立了飞行器高精度轨道动力学模型、在轨试验约束条件模型；利用数学仿真验证了在轨试验窗口设计方法的正确性。

地面测控；光照约束；反射角；试验窗口

0 引 言

在空间试验任务中，在轨操作试验窗口主要是指满足预定飞行试验条件和任务要求，允许飞行器、有效载荷开展在轨操作试验的有效时间及空间范围。在空间任务论证、设计及飞行试验工作中，首要任务就是完成试验窗口的制定，以确保在飞行试验中飞行器、有效载荷的各个系统能够正常工作、试验任务得以顺利进行[1,2]。

本文通过分析飞行器在轨分离释放及捕获有效载荷操作中影响各系统工作的主要约束条件，建立了确定在轨试验窗口的地面测控约束模型、光照约束模型、太阳高度角约束模型、飞行器本体阳光反射角约束模型及飞行器高精度轨道动力学模型；最后，通过数学仿真验证了在轨试验窗口设计方法的有效性。

1 约束条件分析

本文开展在轨分离、捕获操作试验窗口的主要约束条件如下：

a）地面测控约束：为确保飞行器在轨操作任务实时可控，要求飞行器同有效载荷的近距离操作在地面测控区进行。

b）光照条件约束：飞行器上配备的可见光相机正常工作，要求在轨操作试验在光照区开展。

c）太阳高度角约束：帆板位于飞行器本体右侧，试验过程中电源系统需要持续充电，由此要求对高度角进行极性约束以确保足够的能源条件。

d）阳光反射角约束：定义飞行器本体阳光反射角为太阳光线矢量同飞行器本体负轴的夹角，摄像头正常工作要求阳光反射角须大于摄像头遮光角幅值。

e）飞行器在轨姿态约束：本文飞行器试验任务设计中，要求飞行器本体系轴沿速度矢量方向，轴沿轨道径向。

2 计算模型

2.1 坐标系定义

图1 坐标系定义

2.2 轨道动力学建模

根据经典力学理论可知，飞行器在轨运动关系可描述如下：

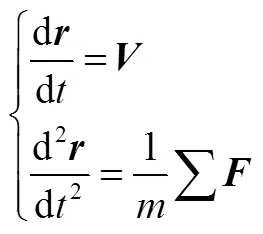
从式（1）可看出，飞行器将在地球引力、大气摄动力、太阳光辐射压力、第三体引力共同作用下绕地球做周期性运动[3~5]。

2.2.1 地球引力模型

地球引力可描述为中心引力与摄动引力加速度之和，引力势函数描述如下：

2.2.2 大气摄动模型

本文中飞行器运行于LEO轨道，受高层大气作用明显，因而需要考虑气动力对飞行轨道的摄动影响。气动力计算公式如下：

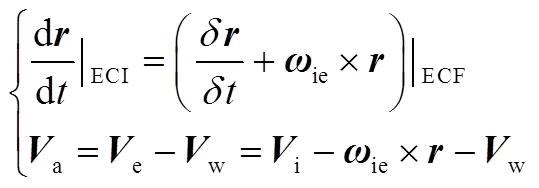
2.2.3 光压摄动模型

飞行器在轨所受到的太阳辐射压力虽然比较小但其累积效应不容忽略，所引起的摄动加速度主要同飞行器质量、受辐射面积大小有关：

2.2.4 三体摄动模型

摄动天体除了对飞行器产生引力作用外，对地球也具有引力作用，引力加速度如下：

由此可以得到地球以外的天体对飞行器产生的第三体摄动加速度为

2.3 约束条件建模

2.3.1 地面测控条件建模

地面站、地球、飞行器三者之间的相对位置关系如图2所示。

图2 地面测控几何关系

2.3.2 光照约束建模

飞行器、地球、太阳及光线三者之间的相对位置关系如图3所示。

图3 光照关系示意

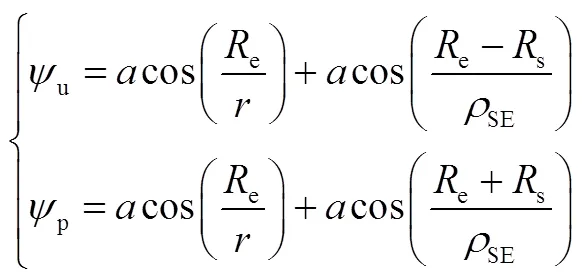
其中，太阳矢量的计算可根据JPL DE405星历得到。

2.3.3 太阳高度角约束建模

在本文研究中，由于飞行器在试验过程中将太阳电池阵锁定于机体右侧，故太阳高度角需要满足相应姿态条件下的极性要求。太阳高度角定义为日心与地心连线同轨道面之间的夹角，计算公式如下：

飞行器机头朝天向沿轨道径向、机腹朝前沿速度方向条件下，要求角大于0满足试验要求；飞行器机头对天沿轨道径向、机腹朝后沿速度反方向条件下，要求角小于0满足试验要求。

2.3.4 阳光反射角约束建模

飞行器本体的阳光反射角定义为太阳光线矢量同飞行器本体负轴的夹角（见图4），与太阳光线矢量对飞行器本体负轴的阳光入射角互补。

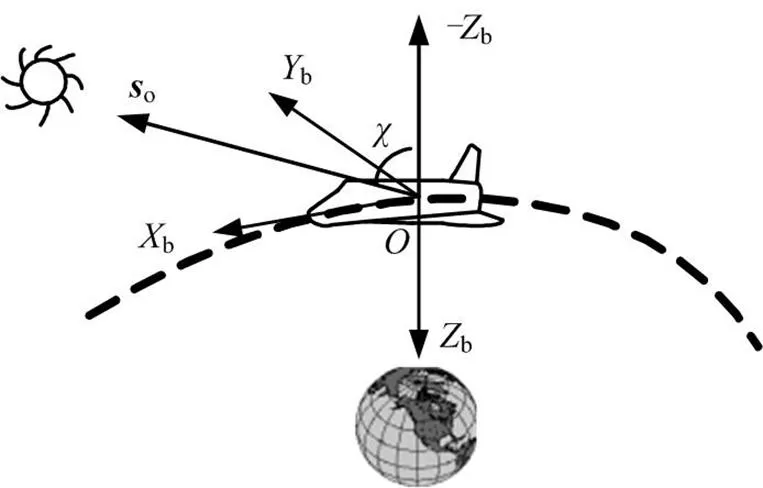
图4 阳光反射角示意

值得注意的是，若采用阳光入射角进行约束建模，则飞行器离开光照区后入射角无实际物理意义，计算中需要进行光照位置判断。

3 试验窗口仿真分析

3.1 主要计算条件

以飞行器开展在轨分离试验为例进行仿真分析及验证。飞行姿态为机背朝前、机头对天状态，起始时间为世界时间2020年9月10日12时整，仿真时长为72 h，地面测控以渭南、青岛、佳木斯三站接力形式进行保障。仿真中所涉及的主要参数如表1所示。

表1 主要仿真计算条件

Tab.1 Main Calculation Condition

参数名称参数值参数名称参数值 半长轴/km7378.132飞行器质量/kg6500 偏心率0.00053迎风面大小/m-213.2 轨道倾角/(°)62.096辐射面大小/m-29.7 升交点赤经/(°)286.631地面站仰角/(°)γ≥5.0 近地点幅角/(°)32.465β角极性/(°)β>0 真近点角/(°)255.213阳光反射角/(°)χ≥68

3.2 仿真结果分析

通过仿真可得试验窗口标识字变化如图5所示。窗口标识字为+5表示可开展在轨试验，为-5表示不满足开展试验条件。由图5可见，72 h内共有19次满足约束条件的试验窗口，窗口持续时长超过5 min的有8次，窗口持续时长小于100 s的有5次；窗口最大时长686.2 s、最小时长21.1 s。由此可知，若飞行器在轨操作试验动作复杂，则需要飞行器在轨等待窗口宽度较大、能够满足试验动作时长要求的窗口条件。

图5 窗口标识变化

图5中测控标识为+2、-2分别表示飞行器对地面站的可见与不可见，利用3个站接力观测，平均每天8~9次可见机会。利用单个地面站计算结果同STK进行对比，可观测时间的相对偏差在2 s以内。图6为地面站仰角变化，从图6中可见，地面站仰角一直在-90°与+90°之间周期性的变化，变化周期约1天，同地球自转周期相近。

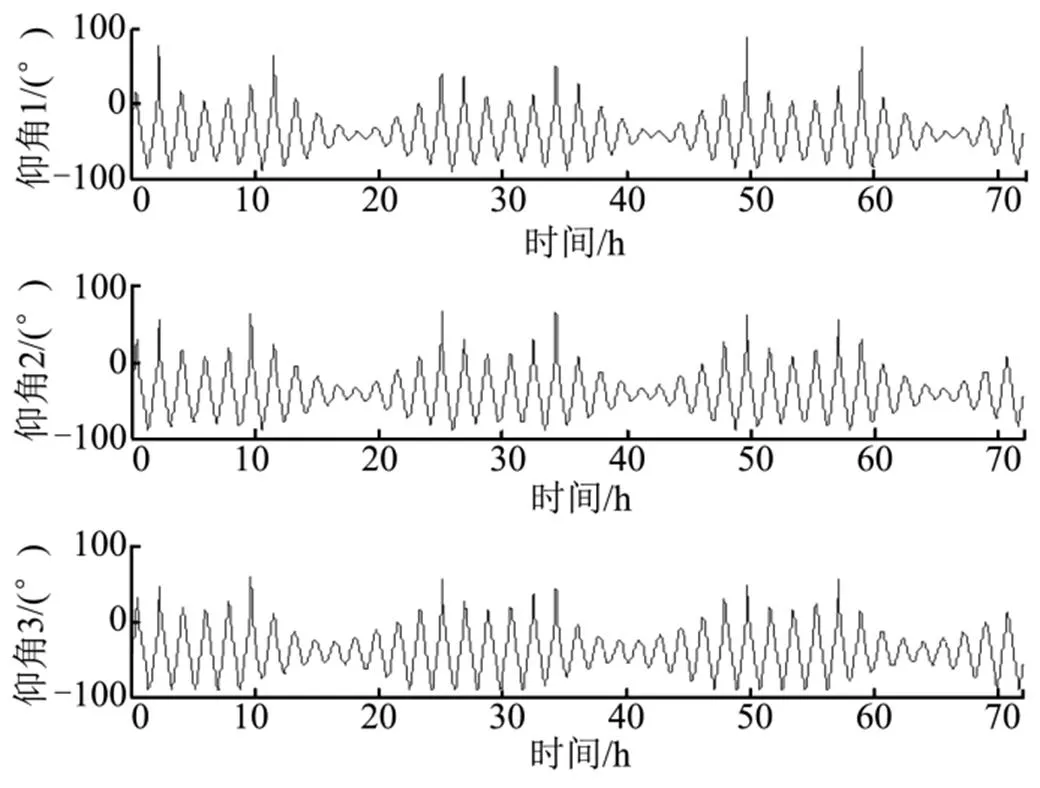
图6 地面站仰角变化

图5中光照标识为+1代表飞行器在光照区、为0代表在半影区、为1代表在阴影区。从图5中可见，飞行器在第3天会出现全光照条件，同STK软件比对结果一致。太阳高度角及飞行器本体的阳光反射角变化如图7所示。太阳高度角3天内在54.9~61.0°之间变化，这种变化与太阳、地球、飞行器的相对位置有关；同STK软件计算结果相比，太阳高度角的相对计算偏差小于0.005°。本体阳光反射角在55.0~124.9°之间周期性变化，变化规律同轨道周期相近；同STK结果相比，本体阳光反射角的相对计算偏差在0.05°以内，能够满足试验设计需要。

图7 太阳高度角与本体反射角变化

4 结 论

高精度在轨试验窗口设计是影响飞行器成功开展在轨操作试验的关键条件，本文根据飞行器在轨任务设计需求完成了在轨试验窗口设计方法研究，并应用于相关任务设计之中。首先，结合飞行器在轨近距离操作试验任务特点，梳理并确定了影响飞行器各系统正常工作、允许开展试验的主要约束条件；其次，结合任务特点，考虑高阶地球非球形引力摄动、高层大气摄动、太阳光压摄动、日月三体引力摄动建立了飞行器的高精度轨道动力学模型及试验约束模型；最后，设计算例、利用数学仿真验证了试验窗口设计方法的正确性。

[1] 周文勇, 宋少倩, 陈益. 一种用于计算上面级发射窗口的方法[J]. 导弹与航天运载技术, 2018(2): 9-12.

Zhou Wenyong, Song Shaoqian, Chen Yi. A method for calculating the launch window of the upper stage[J]. Missiles and Space Vehicles, 2018(2): 9-12.

[2] 茹家欣. 火星探测轨道的数值分析[J]. 中国科学(E辑: 技术科学), 2009(3): 528-534.

Ru Jiaxin. Numerical analysis for Mars exploration orbit[J]. Science in China (Series E: Technological Sciences), 2009(3): 528-534.

[3] 王志刚, 施志佳. 远程火箭与卫星轨道力学基础[M]. 西安: 西北工业大学出版社, 2006.

Wang Zhigang, Shi Zhijia. Remote rocket and satellite orbital mechanics foundation[M]. Xi’an: Northwestern Polytechnical University Press, 2006.

[4] 赵育善, 师鹏. 航天器飞行动力学建模理论与方法[M]. 北京: 北京航空航天大学出版社, 2012.

Zhao Yushan, Shi Peng. Spacecraft flight dynamics modeling theory and method[M]. Beijing: Beihang University Press, 2012.

[5] Oliver M, Eberhard G. Satellite orbits models, methods and applications[M]. Berlin: Springer Verlag Berlin Heidelberg, 2000.

Research on High-precision on-orbit Test Window Calculation Method

Wang Zheng

(China Academy of Launch Vehicle Technology, Beijing, 100076)

In space missions, propriate On-orbit Test Window is the guarantee for the mission. Considered the Ground Tracking System’s constraint, Visible Light Camera’s lighting constraint, Solar elevation angle’s constraint and the Flying Vehicle’s reflection angle constraint, the orbital dynamic model and the on-orbit test constraints’ calculation model have been established, while the trial is carrying out. The effectiveness of Multi-constraints On-orbit Test Window Calculation Method is verified by mathematical simulation.

ground tracking; lighting constraint; reflection angle; on-orbit test window

V412.4

A

1004-7182(2020)02-0023-05

10.7654/j.issn.1004-7182.20200205

王 征（1986-），男，工程师，主要研究方向为飞行动力学与控制。

2019-05-06；

2019-06-06