气动比例位置系统速度反馈与不完全微分PID控制

孙瑞芳，张晓龙，梁文凯，谢晓全

(昆明理工大学 机械工程学院，云南 昆明 650000)

气压传动具有简单快速和安全可靠等特点[1]。气压位置控制系统一直以来都是气动技术的一个重要内容[2]。随着工业自动化的发展，气动技术在生产自动化的各个领域应用日渐广泛，气动位置控制系统的精度和稳定性的优化也日益重要。

PID控制的算法简单，且具有鲁棒性好和可靠性高等特点[3]，在过程控制和运动控制中得到广泛应用，在建立精确数学模型的确定性控制系统方面尤为适用[4]。但在生产实践中，往往很多问题使用常规的PID控制器难以达到实践要求。

冯子通等采用不完全微分型PID算法对电液执行机构控制，得到调节速度快、过程平缓且精度高的效果[5]。强宝民等通过对PID的积分项和微分项改进，提高了电液比例位置控制系统的精度和稳定性[6]。故本文引入速度反馈，并结合不完全微分型PID对气动比例位置系统的响应时间、精度及稳定性进行分析。

1 气动系统数学模型推导

气动比例位置系统主要由比例方向阀、气缸、位移传感器、A/D和D/A装置组成[7]。

1.1 气缸力平衡方程

当单作用气缸处于工作状态时，根据牛顿第二定律，其力平衡方程[8]如下所示

M(d2y)/(dt2)+fdy/dt=p1A1-p2A2-FL-Ff

(1)

式中，M为气缸活塞和惯性负载质量之和；y为活塞位移；f为粘性阻尼系数；p1和p2为气缸两腔的压力；A1和A2为气缸两腔作用面积；FL为气缸外负载力;Ff为包括静摩擦力和库仑摩擦力的气缸摩擦力。

1.2 比例阀的数学模型

通常情况下，阀控缸系统中，比例阀的数学模型[9]为

(2)

式中，U0为比例阀的输入电压；Kw为传感器增益；ω0为比例阀的固有频率；ξ0为比例阀的阻尼比。

1.3 比例阀阀口流量方程

由于气体经过阀口的过程较为复杂，在满足假设条件的情况下，可将其过程视为理想气体的一维等熵流动，运用Sanvile流量公式[10]计算。

一般情况下，当气缸容腔1进气，气缸容腔2排气时，则气缸容腔1中气体流动状态为亚声速，气缸容腔2中气体流动状态为声速。考虑在零位附近的小增量Δx，比例阀的气体质量流量方程可线性化得

(3)

1.4 比例阀流量连续性方程

基于系统气体假设，对于工作腔1，气缸进气腔和排气腔的质量流量应与气缸容腔内质量变化保持一致，故其压力-流量方程[11]如下所示

(4)

理想气体状态方程为

(5)

式中，V1为气缸容腔1体积；R为气体常数;T1为气缸容腔1的温度。

气缸容腔1的实际温度T1与初始温度T1s之间满足绝热过程如下

(6)

式中，k=1.4，为绝热指数。

式(6)对时间求导，带入式(5)中，可得气缸容腔1气体动态过程表达式

(7)

同理可得

(8)

1.5 气动比例位置系统传递函数

将式(3)、式(7)和式(8)改写为增量形式，再进行拉氏变换，并联立可得

(9)

结合式(2)，可得气动比例位置系统总模型方块图如图1所示。

即系统的传递函数为

(10)

(11)

该系统的传递函数由比例环节、积分环节和二阶振荡环节组成。将其中所用参数带入上式中得

用MATLAB绘制该开环系统Bode图如下。

由图可知，该系统幅值特性比相频特性先交于横轴，且幅值裕度为22.43 dB，相位裕度为89.12°，故系统是相对稳定的[12]，可满足生产实践要求。

2 控制策略研究

2.1 常规PID

PID控制器是将偏差的比例、积分和微分通过线性组合的方式[13]，来达到控制被控对象的目的。图3为PID控制系统原理框图。

PID控制器根据给定量和实际输出量之间构成控制偏差

e(t)=y0(t)-y(t)

(12)

PID控制规律和写成传递函数形式为

(13)

(14)

式中，kp为比例系数；T1为积分时间常数，TD为微分时间常数。

2.2 不完全微分PID控制算法

比例环节是将偏差信号成比例的向控制系统反应以减小误差、加快系统的响应速度、提高系统的调节精度。积分环节的存在主要是为了消除系统稳态误差[14]。微分环节则可在早期反映偏差信号的变化趋势，提前引入有效的修正信号，达到及时的改善系统的动态特性的效果，使系统的反应速度加快，减少反应时间。

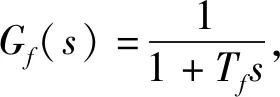
如上图所示，其传递函数为

(15)

将上式离散化，并取uD(n)写成微分方程，取采样时间为Ts，并将其离散化，整理可得

(16)

uD(n)=KD(1-β)(e(n)-e(n-1))+βuD(n-1)

(17)

由上式可见，不完全微分PID控制算法中uD(n)增加了一项βuD(n-1)，但微分系数由kd下降至(1-β)kd，削弱了微分强度，延长了微分作用时间，抗高频干扰，实现微分超前调节。

2.3 加入速度反馈的不完全微分型PID

软反馈即反馈校正信号不直接比例于系统的输出信号，而是将输出信号经过相应处理加工之后得到的，在反馈校正中应用广泛。速度反馈控制就是将输出量的速度信号采用负反馈形式反馈到输入端，并与误差信号进行比较所构成的回路。

速度反馈具有良好的平稳性与快速性，如果在比例伺服系统中，将速度反馈引入到电液比例阀控缸位置系统中，即在控制系统中引入活塞杆位移的微分[15]，可使系统相位超前，在提高液压缸的响应速度的同时，增大阻尼增大，减小振荡及超调，从而提高系统的平稳性。

3 仿真分析

瞬态响应能够直观反应气动比例位置系统动态性能的优劣，是判断其性能的重要评价指标。故基于气动比例位置系统传递函数利用MATLAB对阶跃信号进行仿真，可得到无校正的系统阶跃响应(图5)以及普通PID、不完全微分型PID和引入速度反馈的不完全微分型PID校正的对于阶跃信号响应的对比图(图6)。

如图5中，在阶跃信号作用下，前期有小幅震荡，系统2.5 s,才趋于稳定，响应时间过长，系统反应滞后，稳态误差过大。该情况下系统的控制精度达不到要求，且系统响应不够平稳，需要引入适当的校正方法对系统进行改善，以优化其动态特性。

如图7中，在阶跃信号作用下，通过引入速度反馈的不完全微分型PID的响应曲线比普通PID和不完全微分型PID校正的响应时间和稳态误差皆依次递减，响应过程更加平稳。不同校正方法的系统响应时间和稳态误差如表1所示。

表1不同校正方法的系统响应时间和稳态误差Table 1.System response time and steady-state error of different correction methods

引入速度反馈的不完全微分型PID校正的系统阶跃响应曲线，相对于无校正的响应曲线，响应时间降低2.1 s，稳态误差下降0.22 mm，响应速度提升、系统精度提高且系统的动静态特性得到很大的改善。

再分别用普通PID、不完全微分型PID和引入速度反馈的不完全微分型PID对正弦信号进行追踪，对比图如图8所示。

由图8～图10可看出，普通PID对正弦曲线的追踪误差较大；不完全微分型PID的追踪效果虽明显加强，但不如引入速度反馈与不完全微分型PID的追踪曲线与目标轨迹更加贴合。故引入速度反馈与不完全微分型PID的控制精度更高也更加稳定。

4 结束语

本文建立了气动比例位置系统的数学模型来判断其稳定性，并对比无校正、普通PID、不完全微分型PID和引入速度反馈的不完全微分型PID校正的系统阶跃响应曲线和正弦追踪效果。仿真实验表明，引入速度反馈的不完全微分型PID校正方法在改善系统响应速度、系统精度以及动静态特性方面有显著提升。该校正方法为气动比例位置控制系统提供了新思路，也为日后更深层次的优化研究，挖掘控制效果更好、更适合该系统的控制策略提供了参考。