拒绝服务攻击下的弹性事件触发负荷频率控制
2020-04-20刘希懋曾阳阳
刘希懋,曾阳阳
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
负荷频率控制(Load Frequency Control,LFC)作为最有利的辅助服务之一,在电力系统的稳定运行中扮演着至关重要的角色[1]。LFC的主要目的是通过维持系统供需间的功率平衡来保证整个电力系统的频率在标称值,联络线交换功率为设定值[2]。作为一种典型的信息物理系统(Cyber Physical System,CPS),智能电网通过将计算、通信网络和物理实体进行深度交互、融合,以实现对大型物理系统和信息系统的实时感知、动态控制和信息服务等[3]。智能电网的建设使得无线通信网络等开放网络被大量应用[4]。然而,开放网络由于其开放、共享的特性,也使得电网更易于遭受恶意网络攻击,给电网安全稳定运行造成危害。因此在实际应用中对电力系统的设计、运行提出了更高的要求。
在各种各样的网络攻击中,阻止网络化系统元件之间通信的拒绝服务(Denial of Service,DoS)攻击是攻击空间中最容易实现的攻击方式,其在负荷频率控制系统中最为常见[5]。围绕网络的安全性问题,国内外学者针对不同网络攻击形式进行了广泛的研究[6-9]:文献[6]使用切换系统理论,探究了DoS攻击对电网LFC系统的影响,并比较了不同DoS攻击形式下的系统动态性能;文献[7]针对虚假数据注入攻击不容易监测的特性,提出了一种基于异常的攻击监测和识别方法,并通过对三区域电力系统进行仿真,验证了该方法的有效性;文献[8]使用博弈论方法并结合风险评估理论研究了智能电网自动发电控制系统的安全性问题;文献[9]考虑网络丢包的非理想网络情形,提出了一种针对有限能量DoS攻击的最优攻击策略,并给出了相应的应对策略。值得注意的是,上述文献中的通信方式均采用时间触发机制。当系统处于稳定状态时,机械性的进行数据传输无疑会浪费带宽资源,会给通信网络造成带宽压力,进而影响系统性能。
为了更高效的利用网络资源,近年来国内外学者针对不同网络环境提出了新的通信机制,如事件触发控制[10]、自触发控制[11]、周期事件触发控制[12]、模型预测事件触发控制[13]等。然而,由于这些通信机制的设计过程中均未考虑通信网络遭受恶意网络攻击的情形,因此相关的稳定性分析及控制器设计的方法在网络攻击存在的情况下将不再适用。
针对上述问题,本文对多区域互联负荷频率控制系统的事件触发参数和控制器增益的联合设计问题进行了研究。首先,文中提出了一种周期性弹性事件触发机制,其能够在减轻带宽压力的同时消除DoS攻击对LFC系统的影响,且更适用于实际的执行。然后,构建了一种基于弹性事件触发机制和DoS攻击的时滞切换系统模型。接着,应用Lyapunov稳定性理论及线性矩阵不等式技术等推导了切换系统的稳定性判据,并进行了触发参数及控制器增益的联合设计。最后,在MATLAB/Simulink数字仿真平台对所提方法有效性进行了仿真验证。
1 多区域电力系统LFC建模
1.1 周期性DoS攻击下的多区域LFC模型
图1所示为弹性事件触发机制下的i控制区域动态模型,其前向通道和反馈通道同时遭受周期性DoS攻击。首先,不考虑网络攻击时,通过使用传递函数和拉普拉斯正反变换等理论,可以得到[14]
(1)
其中,Δfi、ΔPmi、ΔPvi和ΔPdi分别指i控制区域的频率偏差、发电机机械输出偏差、阀门位置偏差和负荷扰动偏差;Mi、Di、Ri、Tgi和Tchi分别指i控制区域的发电机转动惯量、发电机下垂系数、转速降、调速器时间常数、涡轮机时间常数;Tij指控制区域i和控制区域j的同步系数;ΔPtiei为i控制区域的联络线交换功率。定义xi(t)=[ΔfiΔPmiΔPviΔPtiei]T,i控制区域的状态空间模型为
(2)
进一步定义x(t)=[x1(t),x2(t),…,xn(t)]T,u(t)=[u1(t),u2(t),…,un(t)]T,ΔPd(t)=[ΔPd1(t), ΔPd2(t),…,ΔPdn(t)]T。
整个电力系统的状态空间模型可以表示为
(3)
当(3)处于稳态时,整个电力系统可表示为
(4)
通常,传感器以固定采样周期h进行周期采样,采样时刻序列可以表示为S1={0,h,2h,…,kh}。因通信机制的不同,采样数据被部分或全部传输到通信网络,即S2={0,t1h,t2h,…,tkh}⊂S1。其中序列S2是触发的采样序列。这样,控制器可以表示为
(5)
其中,K指控制器增益。
需要注意的是,本文旨在对网络攻击下的多区域LFC系统进行弹性事件触发机制和控制器的联合设计研究。对非理想通信网络诱导的通信延时、数据丢失、无序分组等不做考虑。
为了分析清楚DoS攻击对系统性能的影响,考虑一种周期性干扰信号[15-16],以如下方式干扰通信信道
(6)

(7)
其中,x(tk,n+1h)表示在释放时刻tk,n+1h成功传输的采样状态,k∈{0,1,…,k(n)}=K(n),t0,n+1h=nT,(h (8) 首先,回忆下传统事件触发机制[10] eT(ikh)Φe(ikh)>σxT(tkh)Φx(tkh) (9) 步骤1 考虑了DoS攻击时的触发时刻为 (10) 其中,k表示在第(n+1)个攻击周期内触发次数。 (11) 其中,ψk,h=sup{tk,n+1h+mh (12) 结合式(11)~式(12),区间L1,n可表示为 (13) 通过定义如下的两个分段函数 (14) 和 (15) 事件触发采样状态可以表示为 (16) 其中,φk,n(t)=[0,h)。 如式(8)所示的LFC切换系统可表示为 (17) 其中,θ(t)是补充的初始状态条件,有θ(0)=θ0,且状态误差满足 (18) 为了式(17)分析系统的稳定性,定义如下的切换信号 (19) 对于ζ(t)=i∈{1,2}令 (20) 由此,式(17)LFC切换系统可重新表示为 (21) (22) 如果存在对称正定矩阵Pi、Qi、Ri、Wi、Φi和矩阵Mi、Ni、Zi,i∈{1,2},有上述不等式和 (23) 其中,γ=e2(α1+α2)h,在DoS攻击式(6)下的式(20)所示LFC切换系统是指数稳定的,衰减率ρ=ω/(2T)。 根据定理1,给出了LFC增益K和触发参数Φ的协同设计方法。 (24) (25) (26) (27) (28) (29) 其中 另外Λ1={Λ1uv}Λ2={Λ2uv}是对称矩阵,其中 本文选择一个两区域电力系统验证所提方法的有效性,系统参数见文献[17],系统状态向量x(t)=[ΔPtie,Δf1,ΔPm1,ΔPv1,Δf2,ΔPm2,ΔPv2]T。通过简单计算,系统状态矩阵和输入矩阵如下 A= 令T=2 s,Toff=1.68 s,μ1=μ2=1.05,α1=0.13,α2=0.5,σ=0.2,h=0.01,λi=mi=χi=φi=8,i∈{1,2},可得 K= Φ=105× 然后,选择LFC切换系统的状态向量的初始值为x0=[1,0,0,0,0,0,0]T仿真时间设置为30 s。两区域的联络线功率交换偏差和频率偏差如图2所示。事件发生器的释放间隔和LFC弹性切换系统的控制输入分别如图3和图4所示。周期性DoS干扰信号如图5所示。由图2到图5可以看出:(1)联络线交换功率偏差和频率偏差均迅速收敛为零,式(20)的LFC切换系统在周期性DoS攻击下是稳定的;(2)所设计弹性事件触发机制能够消除DoS攻击的影响。这些结果证明了所提控制策略的可行性。 本文研究了恶意DoS攻击下LFC系统的安全性问题。所设计的弹性事件触发机制能够在提高LFC通信信道带宽利用率的同时消除DoS攻击的影响。为在同一框架下分析弹性事件触发机制和网络攻击,提出了一种LFC切换系统模型。通过使用李亚普洛夫理论,得到了切换系统的指数稳定性判据;此外,给出了一种触发参数和LFC增益的协同设计方法;最后,通过一个仿真案例验证了所提控制策略的有效性。1.2 弹性事件触发机制设计和弹性切换系统构建
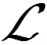
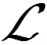



2 弹性事件触发LFC设计
2.1 切换系统指数稳定性分析
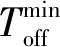
2.2 弹性控制器设计
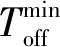

3 案例分析
4 结束语
