也谈小学数学游戏的开发与运用

杨军

摘要：数学游戏的显性表征是“游戏”，即有趣、有规则。有趣，能激发儿童的学习动机;有规则，就有竞争，儿童的智慧就会被“开启”。隐性表征是“数学”，即具有较强的启思性、探究性，能启发儿童的数学思考和探究。可以说，数学游戏将数学的学习情趣和理性精神融为一体。在教学中开发与运用数学游戏的具体做法有：创新游戏设计，促学生产生认知兴趣;强调游戏规则，让学生享受挑战乐趣;深化游戏体验，使学生体悟思维理趣;注重游戏评价，引学生感受創造奇趣。

关键词：数学游戏;设计;规则;体验;评价

特级教师余颖在《数学小游戏——指向学生自由生长的教学新范式》一书中这样定义“数学游戏”：“我们把一些蕴含数学道理，并且运用数学知识或者数学方法的智力游戏归结为数学游戏。数学游戏不单纯是游戏，也不是一般意义上的玩，它是将数学问题蕴含在游戏中，从而让做游戏的人获得数学活动的经验，潜移默化地掌握数学知识、思想与方法。”

数学游戏的显性表征是“游戏”，即有趣、有规则。有趣，能激发儿童的学习动机;有规则，就有竞争，儿童的智慧就会被“开启”。隐性表征是“数学”，即具有较强的启思性、探究性，能启发儿童的数学思考和探究。可以说，数学游戏将数学的学习情趣和理性精神融为一体。不少教师在教学中开发并运用数学游戏，从游戏设计到游戏评价，积累了一些实践成果，笔者试做总结。

一、创新游戏设计，促学生产生认知兴趣

为了促使学生产生浓厚的认知兴趣，教师可基于教学内容，创新游戏设计，巧妙地变学具为“玩具”。

例如，教学《圆锥的体积》一课，一位教师带领学生“玩转三角板”，游戏流程如下：

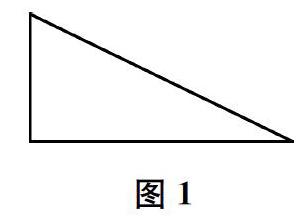
1.将一个直角三角板（如下页图1）以其中的任意一条直角边为轴旋转一周，旋转后得到什么图形？旋转后的两种图形体积相同吗？

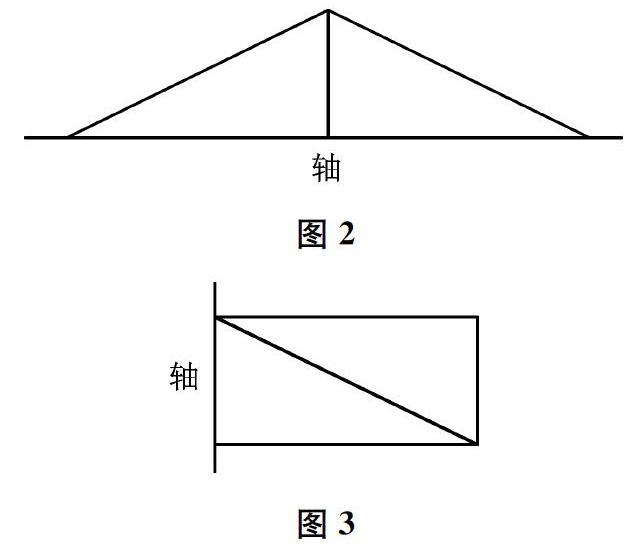
2.将两个完全一样的直角三角板拼成大三角形（如图2）、长方形（如图3），大三角形以最长边为轴旋转一周，长方形以宽为轴旋转一周，求各自旋转后所得图形的体积。两种拼法中每个三角板旋转一周后所得图形的体积相同吗？

3.小组合作，将四个完全一样的直角三角板拼成长方形（如图4、图5），分别以长为轴或宽为轴旋转一周，每个三角板旋转后所得图形的体积是否相等？

熟悉的三角板，成了有趣的“玩具”，并且玩法多样。游戏1中，同样的三角板，以不同长度的直角边为轴旋转一周所得到的图形的体积却不相同。游戏2中，学生可以发挥想象，并发现趣味现象：图2的拼法，两个三角板旋转后所得图形的体积相同;图3的拼法，两个三角板旋转后所得图形的体积不相同。进一步辨析可知：图3的拼法，每个三角板的面积是拼成的长方形面积的一半，而旋转后各自形成的图形的体积却并不是整个圆柱体积的一半（一个是圆柱体积的三分之一，一个是圆柱体积的三分之二）。这与学生一开始的推测（受“面积相等”思维定式的影响，绝大部分学生认为体积也相等）明显矛盾。游戏3中，学生在动手玩和想象中更深刻地认识到：图4的四个三角板中，有两对三角板旋转后所得图形的体积分别相同;图5的四个三角板旋转后所得图形的体积均不相同（这与大部分学生的猜想明显不一致）。

二、强调游戏规则，让学生享受挑战乐趣

游戏应遵循规则。在规则下进行公平、公正、公开的竞争，是游戏的灵魂。小学数学游戏规则可以是数学知识方面的要求，也可以是游戏竞争方面的要求。强调游戏规则，甚至巧妙变化游戏规则，往往可以促使学生积极探寻获胜的策略，享受挑战乐趣，展现思维活力。

例如，一位教师这样带领学生开展“抢数游戏”：

首先，教师出示“抢30”游戏规则：（1）从1开始，同桌两人依次轮流报数，每人每次只能报1个数或2个数，不能多报，也不能不报;（2）谁先报到30，谁就获胜;（3）猜拳，谁赢，谁先报数。为了帮助学生明晰游戏规则，教师安排了示范活动，让学生对“从1开始”“依次轮流”“每次报数的个数”“猜拳决定先后”等要求有所感知。示范时，教师采取了让自己赢的策略，让学生感悟到游戏有一定的技巧，启发学生思考：怎样报数才能赢得比赛？在第一次游戏时，学生的反应是相对平淡的。但是随着时间的推移，学生慢慢地熟悉了规则，开始谨慎地报数，竞争之心被激活，火药味越来越浓。这是“游戏”的趣味性在向“数学”的探究性转变。

接着，教师改变游戏规则：其余规则不变，谁先报到40，谁就获胜。在适应规则变化的过程中，学生逐步明确获胜秘诀：抢30，要抢到27、24、21……3，要后报数;抢40，要抢到37、34、31……1，要先报数;不管抢30还是抢40，都要三个一组地报，即对方报一个数，自己就报两个数，对方报两个数，自己就报一个数。游戏规则的微妙之变，使学生对“抢数游戏”中蕴含的3的倍数特征有了深刻的理解。

三、深化游戏体验，使学生体悟思维理趣

很多数学游戏中蕴含着“大道理”，教师应当帮助学生深化游戏体验，让他们发现游戏中蕴含的数学知识、数学原理，体悟思维理趣。

例如，棋盘、棋子是学生常玩的游戏道具，很多学生会玩诸如五子棋等游戏。一位教师以它们为载体开展了“乘法原理”的教学：

教师首先出示游戏规则：（1）将A、B、C、D四颗不同的棋子放在4×4的方格棋盘中;（2）每行每列只能出现一颗棋子。在学生观察之后提出问题：一共有多少种不同的放法？如果将A、B、C、D、E五颗不同的棋子放在5×5的方格棋盘中，有多少种不同的放法？将6颗棋子放到6×6的方格棋盘中呢？……学生尝试摆放后展开思考：第一步放棋子A，A可以放在16个方格中的任意一个，所以有16种不同的放法;第二步放棋子B，由于A已经放好，放A的这一行和这一列不能放B，问题转化为在其余9格中放置B;第三步转化为在4格中放置C;最后在仅剩的1格中放置D;得到（4×4）×（3×3）×（2×2）种放法。同理，得到5颗、6颗棋子的放法种数。此时，学生对乘法原理已经有了初步的感悟。顺着学生的思路，教师进行了深化：如果将n颗不同的棋子放在n×n的方格棋盘中，一共有多少种不同的放法呢？学生的思维也随着游戏体验更加深化，他们不再进行实践操作，而是进行数学想象、推理，并发现可能的放法有（n×n）×[（n-1）×（n-1）]×…×（2×2）种，顺利完成了知识的建构。

四、注重游戏评价，引学生感受创造奇趣

在游戏教学中，评价也不可或缺。教师要充分运用多元化的评价手段，激励学生在开放性的游戏中拓宽解决问题的思路，发散想象，感受创造奇趣。

例如，在复习“圆的周长”时，一位教師创设了“滚圆”系列游戏任务，并展开了如下教学：

首先，教师出示初级“滚圆”任务：在一个边长为12厘米的正方形内部，将一张半径为2厘米的圆形纸片沿着它的边滚动一周。同时抛出问题：在滚动过程中，圆心经过了多少厘米？大部分学生通过观察发现，沿着正方形内部滚动一周，圆心经过的路线是一个正方形（如图6），比较快捷地求出了圆心经过路线的长度。教师给予学生最基本的“一星”评价，让大部分学生受到激励;并进行提升式点评：当圆片滚到顶点内侧位置时，圆心正好位于路线正方形的一个顶点。

接着，教师出示中级“滚圆”任务：将一张半径为2厘米的圆形纸片沿着一个边长为12厘米的正方形外围滚动一周。由于内部滚动的思维定式，对于外围滚动，大部分学生不假思索，认为圆心经过的路线也是正方形。教师适时对学生的操作、思路展开评价：真的是正方形吗？它的4个“顶点”有特别之处吗？并借助多媒体慢镜头播放滚动过程。学生恍然大悟：“滚”过正方形4个顶点的路线为圆弧，长度为圆周长的四分之一（如图7），4个四分之一圆正好是一个整圆，所以滚动一圈，圆心经过路线的长度为正方形的周长加上圆的周长。教师给予学生“二星”评价，以鼓励学生的进阶。

最后，教师出示终极“滚圆”任务：将一张半径为2厘米的圆形纸片沿着图8所示的不规则图形外围滚动一周。这一游戏更具挑战性，有的学生认为，圆心经过路线的长度等于这个图形的周长;有的学生认为，就是这个图形的周长加上圆的周长……教师再次借助多媒体进行点拨：这个游戏与前面两个游戏有什么不同点和相同点？当圆形纸片滚动经过哪几个顶点时，圆心经过路线的长度是圆周长的四分之一？在经过哪些位置时，不具备这几个顶点类似的特性？……经过教师的点拨，学生想到了思路：虽然是沿着图形的外围滚动，但仔细分析（辅以实际操作）圆形纸片滚动经过6个顶点的情况，可发现有1个顶点相当于内部滚动（如图9），为“直角顶点”，其余5个顶点相当于外围滚动，为“圆顶点”（即中级任务中的圆弧）。并由此放飞灵感：虽然图形没有标出各段

的长度，但“直角顶点”两边的线段可以平移到一起，得到类似图7的图形（少两段2厘米的线段），进而算得总长度。教师表扬了学生的灵感，并给予完成挑战的学生“三星”评价。

在完成难度逐渐递增的游戏任务的过程中，教师十分注重对学生的评价：有激励性的星级评价，有针对性的“纠错”评价，有开放性的“创意”评价。多元化的评价，促发了学生的灵感，引领学生感受到了游戏活动、数学方法的创造奇趣。

本文系江苏省2017年基础教育前瞻性教学改革实验项目“小学游戏课程的开发与实施”、江苏省南通市教育科学“十三五”规划立项课题“小学游戏课程的开发与实施研究”（编号：GH2016042）的阶段性研究成果。

参考文献：

[1] 余颖，提秀雷.数学小游戏——指向学生自由生长的教学新范式[M].南京：江苏凤凰教育出版社，2017.

[2] 马云鹏，吴正宪.深度学习：走向核心素养（学科教学指南·小学数学）[M].北京：教育科学出版社，2019.

[3] 宋宇.数学思维与生活智慧[M].北京：中国和平出版社，2006.

[4] 刘焱.儿童游戏通论[M].北京：北京师范大学出版社，2004.