高职院校科研绩效评价模型研究

乔维德

（无锡开放大学，江苏 无锡214011）

当代高职院校肩负着人才培养、科学研究、社会服务等基本职能和任务，高职院校教师作为履行职能和任务的主要承担者，其综合能力的高低会直接影响履行职能和完成任务的成效。高职院校开展科学研究，可以更好地促进专业教学和人才培养模式改革，提升专业化水平和社会服务能力。目前，很多高职院校虽然重视科研工作，但往往忽视对科研工作及其成果的绩效评价，导致科研成果片面追求数量、成果水平普遍不高等现象。科研绩效评价的全面实施，能够分析高职院校教师科研综合水平和能力，能够根据评价结果健全完善科研管理政策和制度，优化科研经费分配，引导和调整高校教师科研方向，提高科研管理水平及成效。故此，对科研绩效进行客观评价成为现代高职院校科研管理的核心内容和重要任务。以下基于层次分析法和BP神经网络，建立粒子群—蛙跳算法与改进BP算法优化训练BP神经网络的科研绩效评价模型，进而建立高职院校教师科研绩效评价指标体系，并合理赋予评价体系中各指标权重，为高职院校科研绩效评价提供更加科学化、智能化的评价手段和方法。

一、文献综述

目前，不少高职院校仍套用本科院校甚至本科“双一流”大学的科研评价体系，其评价标准与高职院校科研工作实际存在较大差别。所以，高职院校的科研绩效评价体系需要根据高职院校自身办学定位和时代发展要求，对评价指标进行动态调整，并且实施有效评价。

许多学者对高校科研绩效评价进行多维度研究，蔡爱丽在分析高职院校科研工作特点基础上，确定高职院校教师科研评价指标，利用层次分析法评价教师科研绩效[1]；丁洪提出多目标多属性的高校科研绩效模糊评价模型[2]等。但由于高校科研绩效评价是一项复杂的系统工程，呈现复杂时变的非线性关系，单纯采取传统层次分析法、模糊评价方法来评价高校教师科研绩效，往往会出现较大随机性和局限性。于是有学者利用较强非线性映射功能的BP神经网络来评价科研绩效，如张友海提出基于BP神经网络的科研绩效评价模型结构[3]；朱晴、王晶晶提出一种基于粒子群优化的 BP神经网络评估模型[4]等。以上评价方法在教师科研绩效评估中取得一定成效，但仍存在明显的问题与不足，如BP算法的计算过程复杂、收敛速度慢、易陷入局部最小；粒子群算法的局部寻优能力差，易陷入局部最小等。这些问题会导致评价结果与实际值存在较大偏差，评价结果往往准确度不高，难以客观、精准地评价高校教师的科研绩效。

二、研究目的与研究方法

通过构建科学、规范的科研绩效评价体系和评价方法，最大限度地挖掘和发挥高职院校教师本身及科研经费等科研要素的潜力，促进高职院校科研发展模式由注重成果数量多的粗放型增长向注重成果质量高的集约型增长转变，助推高职院校科研高质量发展，为本研究之目的。

研究方法是基于层次分析法构建高职院校科研绩效评价指标体系，建立BP神经网络评价模型，利用粒子群—蛙跳算法优化BP神经网络初始结构参数，通过改进BP算法训练BP神经网络，最后将训练好的BP神经网络模型用于科研绩效评价。

三、研究成效

（一）科研绩效评价指标体系架构

1.建立递阶层次结构

影响高等职业院校教师科研绩效评价的因素较多，并且各因素之间又存在一定的关联，所以运用层次分析法构建科研绩效评价指标结构体系时，需要遵循以下操作原则。

科研绩效差异化评价原则。评价时要综合考虑不同的学科类型，不同学科领域的科研活动呈现不同的特点和侧重点，科研成果也会有不同的呈现形式和研究价值。

科研绩效持续发展评价原则。科研绩效评价指标要引领学科研究方向，实现教师专业化成长以及学生创新能力培养。

科研绩效不交叉评价原则。评价指标避免指标之间存在因果、交叉等联系，杜绝科研绩效的交叉评价、重复评价等现象。

科研绩效全面评价原则。评价指标要综合考虑科研项目、成果、获奖等各方面因素，指标要系统、全方位地反映科研评价绩效。

在参照蔡爱丽[1]的科研绩效评价指标以及咨询高职院校教师、相关专家学者意见基础上，建立高等职业院校教师科研绩效评价指标体系。该体系具有目标层（A）、一级指标层（B）和二级指标层（C）、三级指标层（X）的四层结构模型，如表1所示。

表1 高职院校教师科研绩效评价层次结构

高职院校教师科研绩效评价为目标层；一级指标层由科研项目、科研成果、指导学生项目组成；二级指标层由课题立项、课题经费、课题结题、论文成果等10项指标组成；三级指标层由国家级科研课题立项、纵向课题资助、SCI收录论文、学术专著、国家发明专利、学生科技竞赛获奖数等51项指标组成。

2.构造权重判断矩阵

利用1—9比率标度法求取高职院校教师科研绩效评价的一级指标权重判断矩阵A-B，二级指标权重判断矩阵B1-C、B2-C、B3-C，三级指标权重判断矩阵C11-X、C12-X、C13-X、C21-X、C22-X、C23-X、C24-X、C25-X、C31-X、C32-X，文中列出的表2、表3、表4分别为一级指标权重判断矩阵A-B、二级指标权重判断矩阵B1-C、三级指标权重判断矩阵C11-X，其它指标权重判断矩阵因版面限制在此略。其中，判断矩阵中A-B中的“5”表示指标B1（科研项目）比指标B3（指导学生）明显重要，“7”表示指标 B2（科研成果）比 B3（指导学生）强烈重要，“9”表示指标 B2（科研成果）比指标 B3（指导学生）绝对重要，而“1／5”表示B3（指导学生）明显没有B1（科研项目）重要，“1／7”表示 B1（科研项目）没有 B2（科研成果）非常重要，“1／9”表示 B3（指导学生）绝对没有B2（科研成果）重要，其它判断矩阵类似。

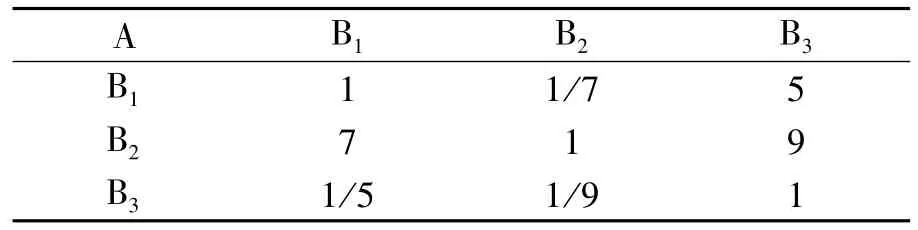
表2 一级指标权重判断矩阵A-B

表3 二级指标权重判断矩阵B1-C

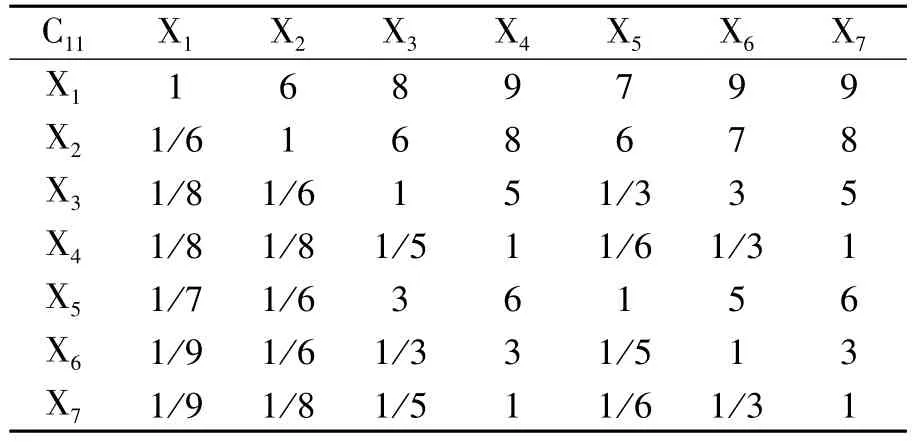
表4 三级指标权重判断矩阵C11-X

3.确定指标单权重

利用方根法得到权重判断矩阵的特征向量，然后通过归一化数学处理求得高职院校教师科研绩效评价各指标相对于上一层指标的权重向量。以一级权重判断矩阵A-B为例，计算过程如下。

①求矩阵A—B每一行的乘积Mi，即：

②求乘积Mi的n次方根，得到

③对方根向量进行归一化处理计算，得到

由判断矩阵A-B的权重向量W＝（W1，W2…Wn）T（n＝3）求得一级指标相对于目标层的权重向量为：

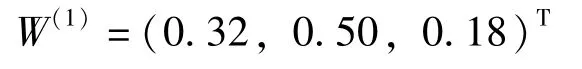
同理，按上述方法计算得到二级指标相对于一级指标权重向量分别为：

同样，按上述方法计算得到三级指标相对于二级指标的权重向量分别为：

4.计算合成权重

通过对各指标层的指标单权重作合成计算后，可以得到三级评价指标X1、X2、X3………X51对目标层的合成权重，即为：W＝W（1）W（2）W（3）＝（0.03264，0.02112，0.01056，0.0048，0.0144， 0.00768， 0.0048， 0.0336， 0.0144，0.0528， 0.0352， 0.0176， 0.00704， 0.0264，0.01408，0.00704，0.01584，0.0187，0.0154，0.0132，0.011，0.011，0.0066，0.0044，0.011，0.0099， 0.0088， 0.02625， 0.015， 0.0188，0.015，0.056，0.042， 0.028， 0.014， 0.015，0.03，0.055，0.0255，0.0165，0.0083，0.004，0.01125， 0.006， 0.00375， 0.063， 0.0378，0.0252，0.0162，0.0324，0.0054）。

（二）科研绩效评价模型建构

首先，采用粒子群—蛙跳算法优化BP神经网络的初始结构，选取影响高职院校教师科研绩效的指标数据作为训练样本对BP神经网络进行学习训练。其次，将训练好的BP神经网络，进行测试检验。最后，将达到标准要求的检测数据用于高职院校教师科研绩效的实际评价，评价模型原理如图1所示。

模型建构具体过程：科研绩效指标数据经过预处理（即归一化）后作为BP神经网络输入变量，网络输出变量S*经过反归一化处理后得到的S为高职院校教师科研绩效的BP网络评价结果。Q为BP神经网络的期望（理想）值，即基于层次分析法计算得出的专家评审结果。ωij为网络输入层与中间层之间的连接权值，Tki为网络中间层与输出层之间的连接权值，中间层、输出层节点阈值分别为θi、θk，E为BP网络输出与期望值之间的误差，BP神经网络在学习训练过程中，通过不断调整结构参数ωij、Tki、θi、θk，直至E达到规定的误差精度。

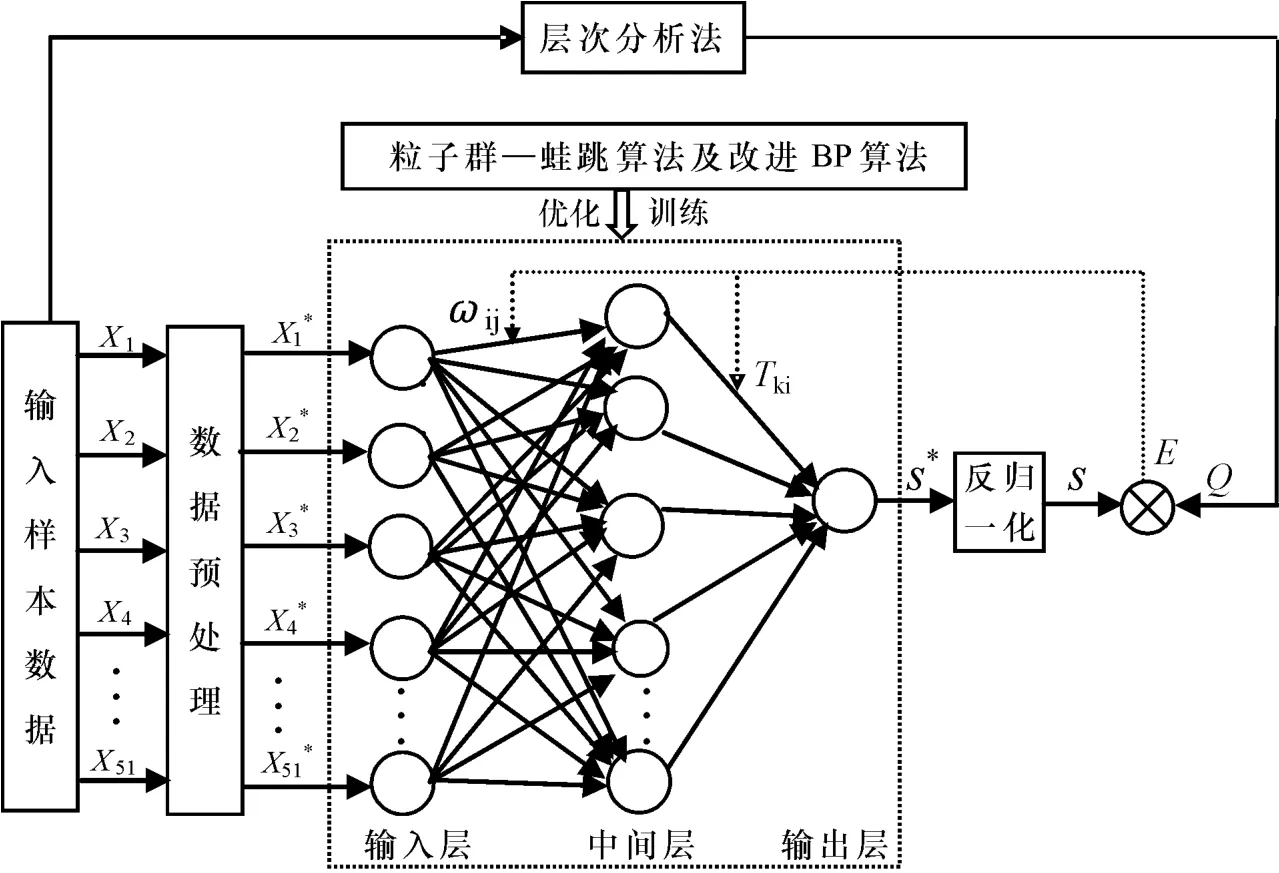
图1 高职院校教师科研绩效评价模型原理图

（三）科研绩效评价模型中BP神经网络优化及训练

图1中高职院校教师科研绩效评价模型中的BP神经网络，其结构参数需要经过反复学习训练实现优化。因为在训练过程中网络输出受参数初始值影响较大，学习很容易陷入局部极值，所以利用粒子群—蛙跳算法对网络神经元之间连接权值及节点阈值等参数进行优化，得到最优初始参数，然后采取改进BP算法训练BP网络，最终实现BP神经网络输出与专家评审结果（即由层次分析法计算而得）之间的误差满足规定精度要求。

网络优化及训练步骤为[5]：确定BP神经网络的拓扑结构，选取科研绩效评价训练数据输入至网络，通过粒子群—蛙跳算法迭代运算和搜寻，当迭代更新次数达到设定迭代数后，输出蛙群最优个体位置，然后将其作为BP网络初始连接权值和节点阈值，再利用引入动量项及自调整学习率的改进BP算法训练BP神经网络，通过不断调整网络权值和阈值，最终实现网络误差在规定范围内。BP神经网络优化及训练的流程图如图2。

（四）科研绩效评价指标模型应用算例

1.数据归一化处理

影响高职院校教师科研绩效的评价指标有51个，各指标量纲、单位并不完全一致。如果选取的样本数据过大，而且将这些数据直接用于输入神经网络，往往会直接拖慢BP神经网络的训练速度以及精度，所以需要将数据进行归一化的数学处理[6]，转换后的数据范围为[0，1]。当然，BP网络输出值同样需要经过反归一化处理，便于将其还原成正常的科研绩效评价值。转换公式中的X*为归一化数据值，X、S分别为原始数据样本的输入和输出量，Xmax、Xmin分别为原始数据最大和最小值。

图2 BP神经网络优化训练流程图

2.BP神经网络结构确定

BP网络输入层神经元节点数n选取为51，分别与高校教师科研绩效评价的51个指标相对应。输出层神经元对应网络输出评价结果S，输出节点数m为1，S设定5个评价等级，分别为优秀[100～90]、良好（90～80]、中等（80～70]、一般（70～60]、较差（60～0]，网络中间层神经元节点数 h由 h＝[（2n+m）1／2，2n+m]确定，通过反复计算测试，确定h为36。BP网络拓朴结构为51—36—1，中间层神经元传递函数采用tansig，输出层神经元传递函数选用purelin，中间层和输出层节点激活函数均采用Sigmoid。

3.参数设置及BP神经网络训练

初始化粒子群—蛙跳算法参数：粒子群规模为 N＝50，ω1＝1.4，ω2＝＝0.5；R1＝R2＝2，粒子群和蛙跳算法的最大迭代次数分别为300、150。BP神经网络训练目标误差精度设定为0.0001。BP神经网络的最多迭代次数为350。选取某高校150位教师科研绩效评价数据的训练样本，训练样本含各评价指标x1～x51数据值以及专家评价得分Q，专家评价分是由层次分析法推算的综合得分，即通过x1～x51指标值与其指标合成权重的乘积之和计算而得，得分Q作为BP神经网络的期望输出值。利用表中150组数据对经过粒子群—蛙跳算法优化的BP神经网络进行训练，学习算法采取改进BP算法，当网络训练步数达到125步时，BP网络满足规定目标误差精度，网络训练速度快、时间短。

4.BP神经网络测试

选取除训练样本以外的另外26组数据作为测试样本，样本数据经过归一化处理后输入至两类BP神经网络，即一类是未优化的BP神经网络，另一类是经过粒子群—蛙跳算法优化的BP神经网络，分别对神经网络输出误差情况进行统计分析，如图3、图4所示。从图中明显得出，没有经过粒子群—蛙跳算法优化BP神经网络输出的科研绩效评价误差，最大可达0.78，而经过粒子群—蛙跳算法优化BP神经网络输出的科研绩效评价误差，最大值小于0.05，误差减少了近16倍。即采取粒子群—蛙跳算法优化BP神经网络对科研绩效进行评价的准确率得到显著提升，所以更加适宜用于高职院校教师科研绩效评价。

四、结语

基于层次分析法、BP神经网络、粒子群—蛙跳算法构建了高职院校科研绩效评价指标体系，架设了BP神经网络评价模型，有效用于高职院校科研绩效评价。通过评价指标的科学选取及其权重合理分配，增强了评价指标体系的科学性、客观性及可操作性。BP神经网络通过粒子群—蛙跳算法优化其初始结构参数，利用样本数据及改进BP算法对BP神经网络加以学习训练，建立了科研绩效评价模型。实践证明，该模型评价速度快、评价精准度高，为高职院校科研绩效评价提供一种崭新的方法，对于高校科研管理与评价工作具有一定的指导意义和推广应用价值。

图3 未优化BP神经网络评价误差

图4 经粒子群—蛙跳算法优化BP神经网络评价误差