重视转化 化曲为直——《圆的面积》教学设计与反思

杨 龙 朱 蕾

【教学内容】

人教版六年级。

【教学过程】

一、谈话引入，引出问题

师：同学们，你们听过嫦娥奔月的故事吗？人类对月球的探索从来没有停过，2018年嫦娥四号卫星成功登陆月球的背面，进行科学探索。这颗具有重要意义的卫星就是在老师的故乡——美丽的西昌发射升空的。西昌是一个山清水秀、人杰地灵、民风淳朴的地方，这里的彝族人民勤劳勇敢、热情善良，每年的农历六月二十四日，是一个重要的节日——火把节。

（课件出示火把节围成圆形的火堆跳达体舞的图片）

师：在这火热的节日里，你看到了哪些与数学有关的信息？

预设：火堆是圆形的、人们跳舞围成的圈是圆形的……

师：同学们真细心，那你想提出什么问题呢？

预设：跳舞的有多少人？跳舞的圈有多大？围着火堆走一圈是多远？火堆的面积有多大？……

师：“围着火堆走一圈是多远？”这个问题实际就是求圆的什么呢？（周长）今天我们重点研究跳舞的圈有多大和火堆的面积有多大这两个问题。同学们想一想，这两个问题实际上就是求圆的什么呢？（板书：圆的面积）

【设计意图：读万卷书，行万里路。数学也要渗透爱国主义教育，数学也要让学生认识不一样的地方，欣赏不一样的美。彝族火把节节日盛况的图片给学生带来美的享受，并从中找到与本课相关的数学信息，有效地激发了学生学习的兴趣和求知欲，使学习成为学生自觉的需求。】

二、巩固旧知，做好铺垫

（课件出示学过的平面图形：平行四边形、三角形、梯形）

师：请回忆一下我们是怎么推导出它们的面积计算公式的。

小结：把未知的东西想办法转化成我们学过的知识来研究是一个非常重要的数学方法。（板书：“转化”）

【设计意图：回顾以前平面图形的面积推导方法，帮助学生唤起旧知，为新知的探究打下良好的基础，便于学生在学习新知识的时候进行迁移类推。】

三、大胆估计，大胆猜想

师：（课件出示以圆的一条半径为边长的小正方形）这个正方形的面积是多少？（r2）

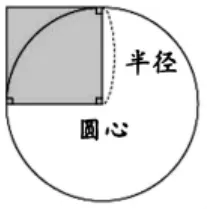
再出示一个小正方形。让学生观察，圆的面积和两个小正方形的面积比较，哪个大？

出示四个小正方形。让学生观察，圆的面积和四个小正方形的面积比较，哪个大？

得出：2r2＜圆的面积＜4r2。

师：请同学们大胆猜一猜，圆的面积大概是r2的多少倍？

【设计意图：用圆的外切正方形的四分之一来与圆进行面积比较，大胆进行猜想，可以初步确定圆面积的取值范围，对于学生思维的发展和后续的学习有积极的作用。】

四、方法迁移，推导公式

1.提出探究问题。

师：光是猜想还远远不够，要准确知道圆的面积是r2的多少倍，那就需要进一步的研究。我们五年级在推导平行四边形的面积时，是把它转化成长方形的，今天我们能不能用“转化”的思路研究圆的面积呢？

2.小组合作，探究面积计算公式。

合作要求：

（1）想办法将圆转化成我们学过的图形。

（2）说一说转化后的图形和圆之间的关系。

（3）推导出圆面积的计算公式。

学生分组合作探究，利用手中的学具想办法将圆转化成学过的图形。教师巡视指导。

3.全班交流。

（学生边展示，边标出转化的过程，并推导出面积公式）

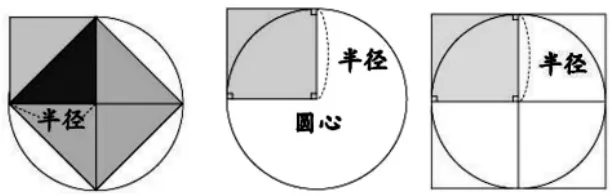
小组1：我们是把圆平均分成16 个小扇形，拼成了一个近似的平行四边形。平行四边形的底相当于圆周长的一半（），高相当于圆的半径r，平行四边形的面积=底×高，所以圆的面积=×r=πr2。

小组2：我们是把圆转化成了一个近似的三角形。三角形的底相当于圆周长的四分之一（），高相当于4r，三角形的面积=底×高，所以圆的面积=

小组3：我们是把圆转化成了一个近似的梯形。梯形的上底相当于圆周长的十六分之三（），下底相当于圆周长的十六分之五（），高相当于2r，梯形的面积=（上底+下底）×高，所以圆的面积=

4.小结方法，感受极限思想。

师：同学们真能干，把圆转化成了我们学过的这些图形，在转化的过程中，什么变了？什么没变？（形状变了，面积没变）

师：老师听到小组汇报的时候，都用了一个词“近似”，你们为什么要加上这个词呢？

（课件出示8 等分、16 等分、32 等分、64 等分……后拼成的平行四边形。让学生体验等分的份数越多，拼出的边看起来就越平，就越接近平行四边形）

师：当这样无限等分下去，圆就会被分成无数条半径，拼出的就是平行四边形了。拼三角形和梯形也是同样的道理。

【设计意图：圆的面积推导和其他平面图形不一样，需要“化曲为直”，用到极限的思想，无限的等分下去，圆就会被分成无数条线段，渗透了以直代曲的辩证唯物主义观点。符合几何学里面点构成线、线构成面、面构成体的思想。学生通过小组合作，同伴间的思维得到碰撞，多样化的转化方法，拓宽了视野，开阔了思路，对于学生创新能力和创新意识的培养有很大帮助。】

五、梳理回顾，小结全课（略）

【教学反思】

一、突破难点促发展

圆的面积公式推导，是小学阶段平面图形最大的一个难点，因为之前学习的平面图形边都是直边的，而圆的边是曲线。研究圆的周长时，用绕线法、滚动法就已经初步渗透了化曲为直的思想，这是研究曲线图形的基本方法。本节课圆的面积更渗透了曲线图形与直线图形的关系，还渗透了极限思想。这样不仅扩展了学生的知识面，而且从空间观念来说，进入了一个新的领域。通过圆面积的公式推导，不仅加深了学生对周围事物的理解，激发兴趣，也为以后学习圆柱打下了基础。

二、渗透转化解新知

提出问题之后，学生就自然会想到如何计算圆的面积？公式是什么？这些都是摆在学生面前的一系列现实的问题。不管怎样都要鼓励学生大胆猜测、设想，说出他们的想法。但也许学生不能很好地想到办法，那么就需要教师引导与以前学过的平面图形建立联系，以平行四边形为例，为学习新知做好准备。这个过程不仅仅是为了回忆，更重要的是渗透一种重要的数学思想，那就是转化的思想，让学生知道新的问题可以转化成旧的知识，利用旧的知识来解决新的问题。

三、小组合作增理解

通过小组合作实验操作，拼出几种以前学过的图形，找到拼出图形与圆的联系，经历公式的推导过程，不但使学生加深对公式的理解，而且还能有效的培养学生的逻辑思维能力和勇于探索的科学精神。大部分学生拼出的是平行四边形，在听其他同学拼出三角形和梯形时，有眼前一亮、耳目一新的感觉，学生在求知的过程中体会到不一样的美，体验到成功的喜悦。