独立自适应调整参数的粒子群优化算法*

张其文，尉雅晨

兰州理工大学 计算机与通信学院，兰州 730050

1 引言

粒子群算法（particle warm optimization，PSO）[1]是由Kennedy 和Eberhart 博士于1995 年共同提出来的一种模仿鸟类群体行为的智能优化算法。该算法已得到了广泛的应用[2-3]。粒子群算法具有实现简单、控制参数少等优点，粒子群算法的收敛性能取决于“勘探”与“开发”之间的平衡，而算法中参数的合理选择对粒子群算法平衡“勘探”与“开发”起重要作用。典型的参数调整包括：惯性权重、学习因子、最大速度、收缩因子等。Zhang 等[4]提出利用贝叶斯技术根据粒子的位置自适应调整惯性权重，提高了算法在多维复杂函数中的收敛精度及速度。Taherkhani等[5]提出了基于稳定性的自适应惯性权重，且学习因子根据惯性权重自适应调整，算法的求解质量和收敛速度都有明显的提高。Tian 等[6]提出了一种介于线性与非线性之间的自适应改变惯性权重的方法，使算法具有更好地平衡“勘探”与“开发”的能力。董红斌等人[7]提出了一种动态调整惯性权重的粒子群算法，使算法具有跳出局部最优的能力。蒋丽等[8]在二阶振荡粒子群算法的基础上改进振荡环节的参数取值，采用互不相同的参数取值调节了粒子群算法的全局与局部搜索能力，提高了种群多样性。黄洋等[9]提出了一种基于S 型函数的自适应粒子群算法，算法根据倒S 型函数的特点对惯性权重进行非线性调整，有效平衡了算法的全局搜索与局部搜索能力。张鑫等[10]提出利用锁定因子及当前粒子的位置自适应调整惯性权重的自适应简化粒子群算法，实验结果表明算法具有较好的收敛能力。此外，Liang等[11]将综合学习策略应用于粒子群算法中，使用粒子的历史最佳位置来更新粒子的速度，维持种群的多样性，有效地防止算法过早收敛。Tanweer 等[12]提出自调节粒子群算法，采用最佳粒子的惯性权重自调节和其余粒子通过对全局最佳位置的感知来确定搜索方向的两种学习策略，算法在大多数问题上表现出良好的收敛能力。李炜等[13]提出一种改进粒子群算法，该算法通过结合特征聚类信息改进了种群的初始化策略，且根据粒子在决策空间中的密度，对粒子进行交互操作，保持种群的多样性，避免过早收敛。

目前，大部分改进粒子群算法均在不同程度上提高了算法的收敛性能，但它们在参数设置方面均基于种群，没有考虑粒子与粒子间进化能力的差异及种群整体的进化情况，在进化的每一代中所有粒子的参数设置是相同的，这样全局搜索与局部搜索就很难达到平衡。针对这一问题，本文提出了独立自适应参数调整的粒子群优化算法，通过独立粒子的进化能力、种群进化能力及进化率来动态调整每个粒子的参数，增强算法平衡全局搜索与局部搜索的能力。同时加入粒子重构策略使进化能力较弱的粒子通过向进化能力较强的粒子进行学习生成新粒子，这既增加了种群多样性，也使算法能跳出局部最优。

2 粒子群算法

1998 年Shi 和Eberhart[14]首次提出将惯性权重添加到粒子群算法的速度更新公式当中去，如下所示：

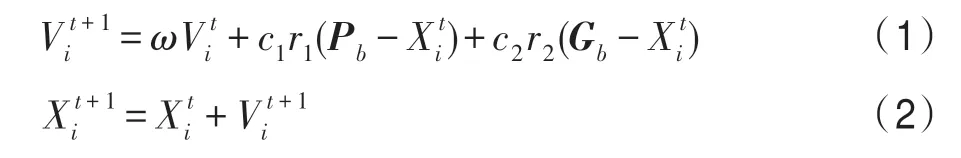
其中，t为当前迭代次数，r1、r2为[0,1]之间的随机数，用来维持种群的多样性。Pb为个体历史最优位置，Gb为群体历史最优位置，c1、c2为学习因子。ω称为惯性权重，它用于表示粒子上一代的速度对当前粒子运动行为的影响。目前使用较多的惯性权重的设置方式是随迭代次数的增加而线性减小：

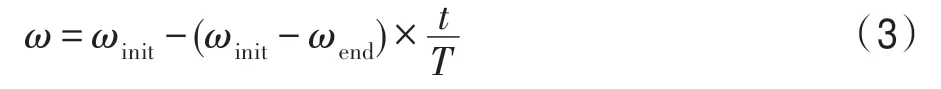
其中，ωinit为初始权重，ωend为最终权重，T为最大迭代次数。

3 参数的调整

在进化过程中，粒子与粒子之间的进化能力、种群的整体进化能力、求解的问题均不同，因此本文在对参数的设置方面充分考虑了这些不同之处，使参数能在不同的情况下进行自适应调整。

定义1（粒子进化能力）在进化过程中，将粒子进化能力定义为该粒子相较于其他粒子能找到的较好解的能力。

定义2（种群进化能力）在进化过程中，将种群进化能力定义为种群中所有粒子能找到比当前最优解更好解的能力。

粒子的进化能力与种群的进化能力计算公式如下：

定义3（进化率）在进化过程中，将粒子的进化率定义为粒子在种群中进化能力变化程度的大小。

粒子在种群中进化能力的进化率计算如下：

若粒子进化能力及种群进化能力都较强时，粒子进化率较小，则粒子在下一代会较多地继承上一代粒子的进化能力，反之亦然。

3.1 自适应惯性权重

本文根据粒子进化能力与种群的进化能力为每个粒子设置自适应惯性权重，这样既保证了粒子的多样性，又方便粒子更好地在空间中进行搜索。独立粒子的惯性权重设置公式如式（7）所示：

综上所述，在t+1 代时每个粒子惯性权重的调整都由第t代时粒子进化能力和种群进化能力共同决定。群体中的粒子能否发现比当前全局最优更好的解决定了粒子的搜索范围，而粒子本身进化能力的强弱则是设置独立粒子惯性权重的关键。

3.2 自适应学习因子

学习因子是体现粒子向自身历史最优学习与向群体历史最优学习能力的两个参数。本文在将学习因子c1设计为递减函数、c2设计为递增函数的基础上根据粒子进化能力的变化率去调整每一代中每个粒子的学习因子。这样的设置方式与其他经典学习因子的取值方式相比，不但能在迭代初期保证粒子的学习能力，加强全局搜索；在迭代后期保证粒子的社会学习，利于局部精准搜索，还通过独立粒子之间不同的进化率，对学习因子进行调整，使粒子结合自身情况调整学习模式。调整公式如下所示：

其中，c1max表示学习因子的最大值；c2min表示学习因子的最小值。粒子在迭代初期应该具有较强的自我学习能力，此时的c1值较大，c2值较小。若某粒子i的进化率较小，那么该粒子相比其他粒子的c1稍大、c2稍小，更有利于该粒子进行全局搜索。随着迭代次数的增加，粒子应该具有较强的社会学习能力，此时的c1值较小，c2值较大。若粒子i的进化率较大，那么该粒子相比其他粒子的c1稍小、c2稍大，更有利于该粒子进行局部搜索。本文中，每个粒子的学习因子均根据粒子进化能力的变化率进行自适应调整。式中的参数取值c1max=2,c2min=0.8。

4 粒子重构策略

为了进一步保障种群多样性，使粒子有跳出局部最优的能力，本文采用粒子重构策略，它的主要思想是从种群中选择出部分进化能力较弱的粒子向进化能力较强的粒子进行学习，重新构造出新粒子。

4.1 粒子的选择

由式（4）可知，在进化过程中，粒子的进化能力与该粒子的适应度值相关，因此本文将粒子适应度值的好坏作为评判粒子进化能力强弱的标准。在使用粒子重构策略前，先将种群中的粒子按照适应度值进行排序，选择出末尾的个粒子作为进化能力较弱的粒子，这部分粒子将进行重构操作。剩余的个粒子为进化能力较强的粒子，是进化能力较弱的粒子进行重构时需要学习的范例。其中由式（10）、式（11）进行确定：

其中，N表示种群的总规模。被选择重构的粒子数是随着迭代次数t的增加而增长的，被选择重构的粒子数最大可达到种群总规模的80%。

4.2 粒子的重构

最后将新生成的粒子与进化能力较强的粒子合并后一起进行下一次迭代。该策略的优势在于它既能有效地拓宽种群的搜索范围，又能保证算法的收敛精度与速度。

5 独立自适应调整参数的粒子群优化算法

5.1 算法的收敛性分析

算法参数的选取和算法的收敛性是决定粒子群算法性能与效率的重要因素，因此对算法的收敛条件及满足收敛时参数的取值范围进行分析是十分有必要的。为了使下面对粒子群算法的分析更加方便直观，在不失一般性的条件下，将粒子的速度与位置的维数从D维简化为1 维，令Pi为粒子i自身找到的最好的位置，Pg为整个种群找到的最好位置，令：

因此可以将PSO 的速度与位置公式简化如下：

再令：

可将式（13）、式（14）表示为：

定义4（平衡点）将R*定义为动态系统R(t+1)=A*R(t)的平衡点，在本文中，平衡点R*必须满足条件：∀t≥0 均满足R(t+1)=R(t)。

根据李亚普诺夫的稳定性可知，系统收敛到平衡点的充分必要条件是A的全部特征值均要小于或等于1。

|A-λE|=0 称为矩阵A的特征方程。矩阵A的特征值为特征方程λ2-(ω+1-φ)λ+ω=0 的解，因此解得线性系统R的两个特征值为：

其中Δ=(ω+1-φ)2-4ω

对Δ=0,Δ＞0,Δ＜0 分别讨论后，得出系统R(t)的收敛域为：

系统收敛的充分必要条件为：

本文根据粒子自身进化与种群进化能力对每个粒子进行自适应独立参数设置，其中参数的取值为ωinit=0.9,ωend=0.4,c1max=c2max=2,c1min=c2min=0.8。根据式（4）～式（9）可得：

由此可得IAP-PSO 中关于参数的设置满足算法的收敛条件，证明该算法具有在搜索空间中收敛到局部最优点甚至是全局最优点的能力。

5.2 算法的具体流程

IAP-PSO 算法的基本步骤：

步骤1 随机初始化N个粒子，初始化参数ωinit、ωend、c1max、c2max、c1min、c2min，最大迭代次数T，问题维度D等。

步骤2 计算粒子的适应度值，找出个体最优Pb与全局最优Gb。

步骤3 根据式（1）、式（2）更新粒子的速度与位置。

步骤4 计算粒子的适应度值，更新个体最优与全局最优。

步骤5 根据式（4）～式（9）计算出粒子i在第t+1代时的惯性权重及学习因子。

步骤6 选择出进化能力较弱的粒子，根据式（12）向进化能力较强的粒子进行学习，重构新粒子，将新粒子与进化能力较强的粒子合并。

步骤7 判断算法是否达到终止条件，若满足，则算法停止并输出最优值；若不满足，跳转到步骤3 继续执行。

5.3 时间复杂度分析

由IAP-PSO 算法可知，其主要包括如下部分：（1）初始化，时间复杂度为O(N×D)；（2）粒子进行速度与位置的更新，时间复杂度为O(N×D)；（3）计算粒子适应度值，更新个体最优及全局最优的时间复杂度为O(N×D)；（4）自适应调整粒子的惯性权重与学习因子，时间复杂度均为O(N×D)；（5）计算粒子的进化能力，选出需要重构的粒子进行粒子重构，时间复杂度为O(N×D)；（6）判断迭代是否停止的时间复杂度为O(1)。因此，IAP-PSO 算法的时间复杂度为O(N×D)。

6 实验分析与结果

6.1 算法的多样性分析

粒子群算法易陷入局部最优点的主要原因就是种群在迭代后期种群多样性下降。以函数Schwefel为例，将IAP-PSO、PSO 算法进行多样性对比。图1为两个算法在迭代初期进行初始化时的种群分布图，图2 为迭代后期两个算法迭代到全局最优值为3 000 左右（算法还未收敛）时的种群分布图。

由图1 可知两算法在迭代初期粒子分布都较为均匀。从图2 中可以看出，两种算法迭代到后期时，IAP-PSO 算法仍保持着较高的多样性，粒子分布均匀，具有强的进化能力。而PSO 算法的多样性明显劣于IAP-PSO 算法，已呈现出聚集状态。

6.2 测试函数

对CEC2013 标准测试函数集中的10 个基准函数进行仿真实验，用于测试IAP-PSO 算法的性能，测试函数的具体信息如表1 所示。

Fig.1 Initial population distribution图1 初始种群分布

Fig.2 Population distribution in later stages图2 后期种群分布

Table 1 10 test functions used in experiment表1 实验中使用的10 个测试函数

6.3 对比算法

为了验证IAP-PSO 算法在求解复杂问题时的性能，将IAP-PSO 算法与动态调整惯性权重的粒子群算法（particle swarm optimization algorithm for dynamic adjustment of inertia weight，DIW-PSO）[7]、综合学习粒子群算法（comprehensive learning particle swarm optimiser，CLPSO）[11]、自调整粒子群算法（self regulating particle swarm optimization algorithm，SRPSO）[12]及标准PSO[13]进行对比实验。为了保证测试的公平性，算法的参数设置均相同：种群规模为40，迭代次数为1 000，分别在D=10、30、50 时独立运行30次。实验环境为：Intel i5 CPU 2.50 GHz，RAM 4 GB，Windows 7操作系统，Matlab R2016a。

6.4 算法性能测试的实验结果与分析

表2～表4 分别是D=10,30,50 时PSO、CLPSO、SRPSO、DIW-PSO 与IAP-PSO 算法在测试函数上的结果，其中包括最优解、最差解、平均值和标准偏差。借鉴文献[15]的数据统计与分析方法，采用显著性水平为0.05 的Wilcoxon 秩检验方法来判断算法性能。其中“+”“-”“～”分别表示IAP-PSO 算法的结果优于、劣于、相当于对应算法的测试结果。

从表2～表4 结果中得出，与其他算法相比，IAPPSO无论在低维还是高维，均能在单峰函数、多峰函数和组合函数中找到更好的结果。从表5的Wilcoxon结果来看，在α=0.05 时IAP-PSO 算法在测试函数上相较于对比算法均获得了明显的优势。值得说明的是，相较其他算法IAP-PSO 算法在求解高维问题时具有突出优势。此外，在图3～图8 中分别展示了算法在部分函数上收敛情况，从图中可以清晰地观察出IAP-PSO 算法在收敛速度与收敛精度上均具有显著优势。虽然IAP-PSO 算法自身也存在不足，当维数增加时，算法的稳定性相比其他算法略显不足，但总的来说，IAP-PSO 算法与其他算法相比，在优化结果上都大有提升。

6.5 算法运行时间对比

为进一步说明IAP-PSO 算法在寻优速度上的优势，使算法在相同的实验环境下独立运行20 次，粒子数均为40，记录算法达到指定收敛精度时的运行时间。如果迭代到200 000 次后仍达不到要求的精度，则用“—”表示，如表6 所示。

Table 2 Optimized results of comparison algorithms on test functions(D=10)表2 对比算法对测试函数的优化结果（D=10）

Table 3 Optimized results of comparison algorithms on test functions(D=30)表3 对比算法对测试函数的优化结果（D=30)

Table 4 Optimized results of comparison algorithms on test functions(D=50)表4 对比算法对测试函数的优化结果(D=50）

Table 5 Results obtained by Wilcoxon test表5 通过Wilcoxon 的测试得到结果

Table 6 Running time of algorithm to achieve specified accuracy表6 算法达到指定精度的运行时间 s

Fig.3 Convergence curve of f1（D=30）图3 函数f1的收敛曲线（D=30）

Fig.4 Convergence curve of f1（D=50）图4 函数f1的收敛曲线（D=50）

Fig.5 Convergence curve of f6（D=30）图5 函数f6的收敛曲线（D=30）

Fig.6 Convergence curve of f6（D=50）图6 函数f6的收敛曲线（D=50）

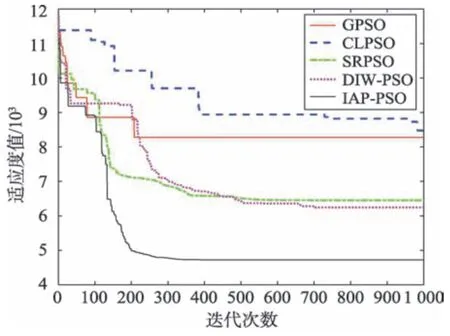
Fig.7 Convergence curve of f10（D=30）图7 函数f10的收敛曲线（D=30）

Fig.8 Convergence curve of f10（D=50）图8 函数f10的收敛曲线（D=50）

由表6 知，在实验环境相同的情况下，IAP-PSO算法达到指定精度要求时所运行的时间要比标准粒子群算法及其改进算法的运行时间更优，从运行时间方面再次验证了IAP-PSO 算法的有效性。

7 结束语

为更好地达到粒子群算法局部搜索与全局搜索之间的平衡，本文提出独立自适应调整参数的粒子群算法。算法利用粒子进化能力与种群进化能力的不同，自适应地调整每个粒子的惯性权重和学习因子。算法中还加入粒子重构策略，使每一代粒子中进化能力较弱的粒子向进化能力较强的粒子进行学习，并重新构造出新粒子，这既增加了种群的多样性，也提高了算法的收敛性能。实验结果表明，在解决高维复杂问题时该算法在收敛速度与收敛精度上都有明显的优势。在部分测试函数中IAP-PSO 算法的稳定性有待提高，并且算法应在实际应用问题中验证其有效性，以上问题将是下一步研究的主要内容。