两阶段不定核支持向量机*

史 娜，薛 晖+，汪云云

1.东南大学 计算机科学与工程学院，南京 211189

2.东南大学 计算机网络和信息集成教育部重点实验室，南京 211189

3.南京邮电大学 计算机学院，南京 210023

1 引言

支持向量机（support vector machine，SVM）作为一种有效的分类技术，已经在实际应用中取得了非常好的效果。尤其在引入核技巧后，SVM 的性能进一步提高[1]。在经典的核SVM（kernel SVM，KSVM）算法中，通常要求核矩阵正定，即核函数满足Mercer定理。但是近年来，在计算机视觉和生物信息等领域，出现了越来越多的非正定度量手段[2-5]，例如：利用最长公共子序列，度量两个基因序列相似性；利用BLAST 评分函数，度量两个蛋白质序列相似性；利用集合操作的交、并等，度量两个事务的相似性；利用人类先验知识，判断两个概念或者单词之间的相似性；计算机视觉领域中的利用正切距离和形状匹配等，度量两个图形的相似性。上述的度量手段往往导致核矩阵的不定，进而使得经典的KSVM 算法无法对这些问题进行有效的求解[6-7]。针对上述问题，越来越多的学者对不定核支持向量机（indefinite kernel support vector machine，IKSVM）展开了广泛的研究。目前IKSVM 的求解算法主要分为两大类：（1）基于核矩阵修正的求解；（2）基于原始不定核矩阵的求解。第一类算法是将不定核矩阵修正为正定矩阵，从而使得经典的KSVM 算法仍然适用。例如，将核矩阵的所有负特征值置零的“Clip”算法、将核矩阵的所有负特征值取绝对值的“Flip”算法、将核矩阵的特征值加上一个正常数以使得所有特征值大于零的“Shift”算法，以及将所有特征值取平方的“Squared”算法等[8]。除了上述将矩阵修正和KSVM 问题求解分开进行的做法外，另一种比较常见的做法就是将矩阵修正和经典KSVM 分类进行联合求解。Chen 等人[9]将原始的不定核矩阵视作一个未知正定矩阵的带噪声形式，并将该正定矩阵的拟合和经典KSVM 分类联合起来作为最终的优化目标。Gu 等人[10]认为不定核矩阵具有低秩的正定近似，从而将核矩阵的低秩正定近似求解和经典KSVM 问题求解联系起来，并进行迭代优化。然而，上述基于核矩阵的正定近似进行IKSVM 问题求解的算法，会使得不定核矩阵的一些有用信息丢失，因此在实际应用中效果并不理想[11-12]。第二类算法直接利用不定核矩阵进行求解，从而解决矩阵的修正过程带来的信息丢失问题。Alabdulmohsin 等人[7]将核矩阵K的每一行看作样本的特征，从而将IKSVM 问题转化成普通的线性规划问题进行求解。Hochreiter 等人[13]将KKT的行看作特征，从而可以利用现有的凸优化算法进行求解。Loosli等人[12]通过探究再生核Kreĭn 空间（reproducing kernel Kreĭn space，RKKS）和再生核Hilbert 空间（reproducing kernel Hilbert spaces，RKHS）之间的关系，提出可以将IKSVM的解与KSVM 的解通过一个映射矩阵联系起来，从而达到IKSVM问题的间接求解。Xu等人[14]从IKSVM优化的主问题出发，提出可以将IKSVM 问题刻画成一个凸差规划问题，从而能够利用现有相关的凸差算法进行求解。Oglic 等人[15]将IKSVM 问题转化成一个约束特征值问题，从而可以利用特征值方程进行问题的求解。然而，上述的IKSVM 算法，均不能较好地解决高维数据所带来的信息冗余和样本稀疏问题。因此，在实际处理高维数据时，通常会采用主成分分析（principal component analysis，PCA）作为数据的预处理方式，然后再进行IKSVM 的处理。但是，这种处理方式也有其局限性，即处理的数据必须是样本的向量表示形式，若给定度量矩阵的结构化数据集，该种处理方式将无法应用。

为了解决高维数据所带来的信息冗余和样本稀疏等问题，本文基于Loosli 等人[12]对IKSVM 稳定化问题的定义，从理论上证明了IKSVM 问题的求解等价为IKPCA（indefinite kernel principal component analysis）和SVM 的依次执行，并提出了一种求解IKSVM问题的新型学习框架：TP-IKSVM（two-phase indefinite kernel support vector machine）。该学习框架将IKSVM 问题的求解分为两个阶段：第一阶段应用IKPCA 技术进行非线性降维以提取数据的主要信息，同时缓解信息冗余和样本稀疏等问题[16]；第二阶段在降维后的特征空间进行SVM，从而进一步挖掘低维空间中判别信息。另外，由于本学习框架不涉及样本的原始向量表示形式，因此TP-IKSVM 的应用更加灵活。在真实数据集上的实验表明，TP-IKSVM在分类性能上优于现有的IKSVM 算法。

2 相关工作

2.1 Kreĭn 空间和RKKS

Kreĭn 空间K 是由两个Hilbert 空间(H+,H-)张成的内积空间，并且满足[12，15]：

（1）∀f∈K,f=f++f-

（2）∀f,g∈K,

其中，f+，g+∈H+，f-，g-∈H-。

如果这里的H+、H-均为RKHS，那么Kreĭn 空间K 就是一个RKKS，可以看出RKKS 是Kreĭn 空间的特例。假设实值对称函数k可以对应到一个RKKS，那么满足k=k+-k-，其中k+和k-是可以分别对应到H+和H-的实值函数。

为后续描述的方便，这里将Kreĭn 空间限定为有限维空间，并用pE表示（有限维的Kreĭn 空间又称伪欧空间，用pE表示）。具体地，pE可以表示为两个欧式空间的直和R(p,q)=Rp⊕Rq，其中Rp和Rq均为Hilbert 空间，相应的内积操作为。引入J=diag(1p′-1q)，则pE空间中的内积可以进一步表示为，其中运算符“*”代表pE空间的内积操作，J代表了pE空间的维度特性，并且满足J=JT=J-1[17]。

2.2 IKPCA

IKPCA[16]是一种非线性降维技术，旨在RKKS 中寻找一组投影方向，使得样本投影点之间的差异最大化。

假设样本在RKKS 中可以表示为Φ={φ(x1),φ(x2),…,φ(xn)}，其中φ为映射函数；特征均值为μ=。设Φ已经中心化，即φ(xi)=φ(xi)-μ。定义RKKS 中全散度矩阵Sκ：

其中，S|κ|=ΦΦT为与RKKS 相应的RKHS 中的全散度矩阵。

因此，IKPCA 的目标函数可表示为：

最后，对K进行特征分解，得到式（3）的最优解：

3 TP-IKSVM

为了引出求解IKSVM 问题的新型学习框架TPIKSVM，本章首先对IKSVM 问题进行形式化的定义，然后基于该定义给出TP-IKSVM 的证明。

3.1 IKSVM

Loosli 等人[12]的研究表明，IKSVM 的求解可以表示成RKKS 中的稳定化问题，即：

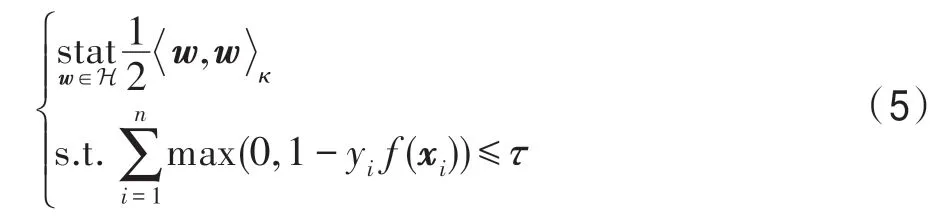
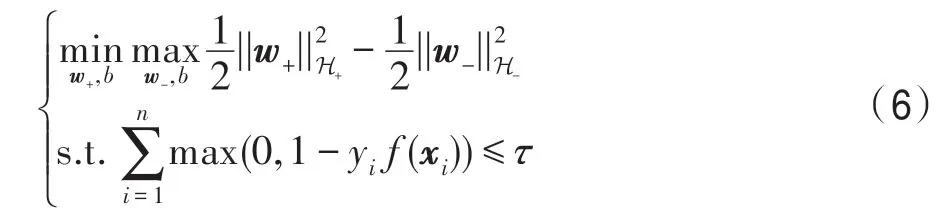
将式（6）的极大化部分等价转换为负的极小化问题，得到：

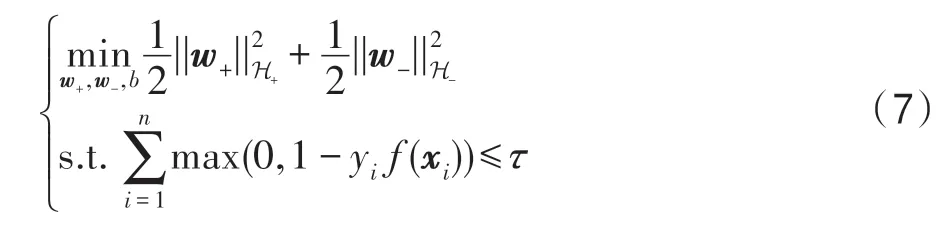
最后，将上述约束最小化问题转换成等价的无约束问题，得到：

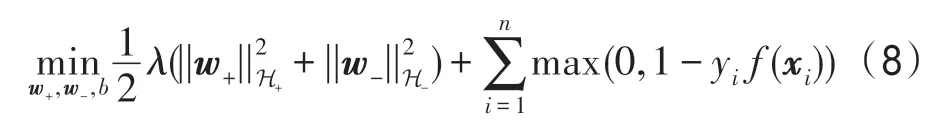
上式记为IKSVM 问题的主问题P-IKSVM。

根据表示定理，得到相应的对偶问题，并记为DIKSVM：

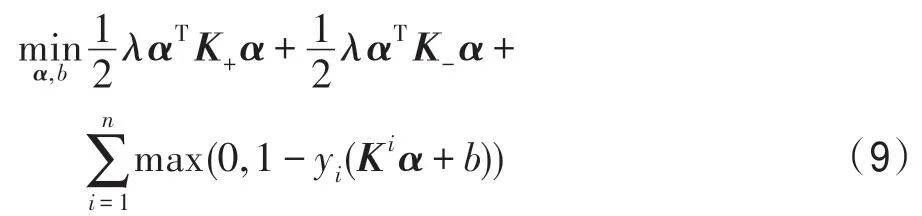
其中，K是不定核矩阵，Ki代表核矩阵的第i行，K+、K-是根据核函数k+、k-所得到的正定核矩阵，并且满足k=k+-k-，K=K+-K-。

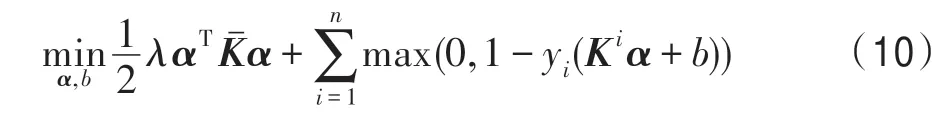
3.2 TP-IKSVM 的证明

TP-IKSVM 学习框架是一种解决IKSVM 问题的新型求解思路。TP-IKSVM 将IKSVM 的求解拆分为IKPCA 和线性SVM 两个阶段。其中第一阶段的IKPCA 作为一种经典的降维技术首先将原始的高维样本数据投影到一个低维空间，从而缓解由于样本维度与样本个数比值较小产生的样本稀疏问题，然后在降维后的空间中进行第二阶段SVM，能够更好地挖掘低维数据的分类信息。为了说明TP-IKSVM学习框架的合理性，引入下面的定理1。

定理1 设α为原始pE空间中D-IKSVM 问题的解，为样本经过IKPCA 降维后pE1空间中的SVM问题的解，则。

证明 记经过IKPCA 降维后，特征空间由原始的pE∈(p,q) 变为pE1∈(p1,q1)，样本特征由Φ(xi) 变为，即：

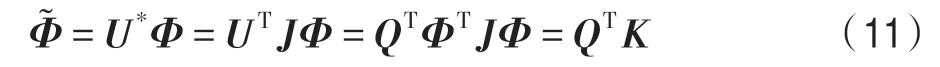
在pE1空间进行SVM，可以表示为如下优化问题：

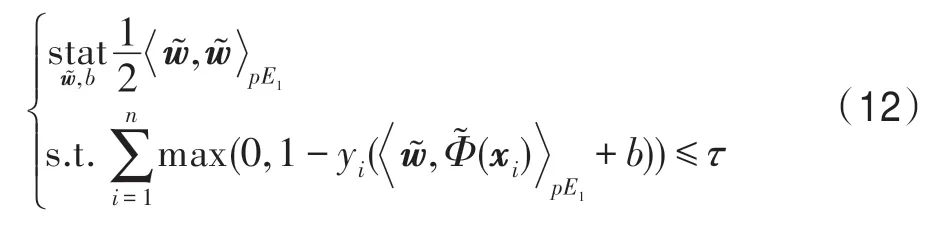
将式（12）等价变换为无约束的优化问题：

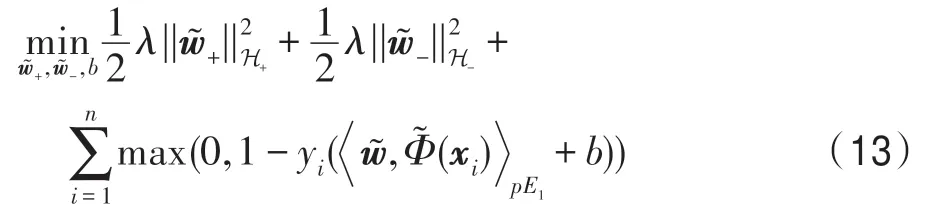
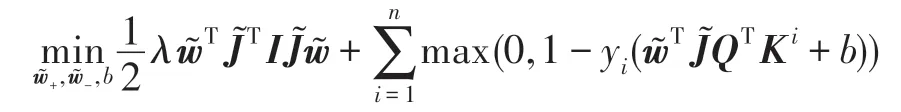
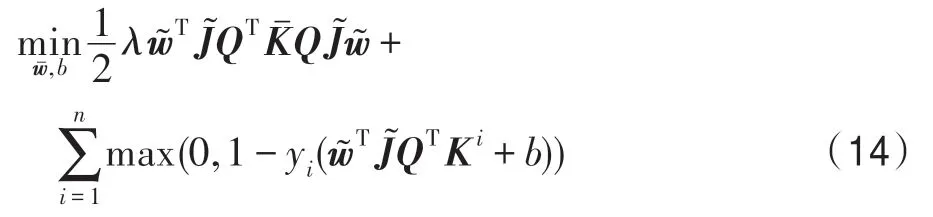
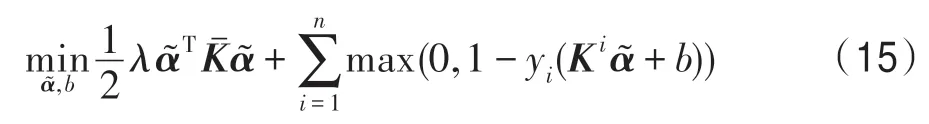
通过定理1，可以发现分两阶段求解的TPIKSVM 和直接求解IKSVM 等价。但是，考虑率到pE1空间的未知，因此求解相对复杂，为了简化第二阶段问题的求解，引入命题1。

证明 在pE1空间对应的Hilbert 空间中进行SVM，等价于下述问题的求解：

根据Hilbert空间的性质可知：

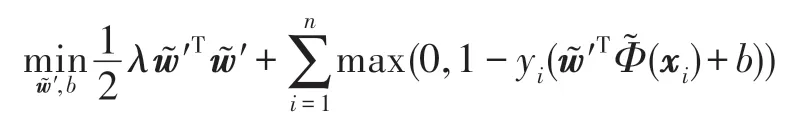
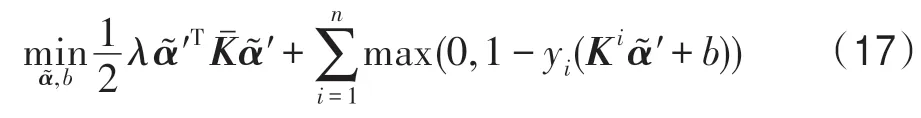
由命题1 可知TP-IKSVM 第二阶段的pE1空间SVM 可以简化为对应Hilbert空间中的SVM。

结合定理1 和命题1，可以看出IKSVM 的求解本质是在IKPCA 降维后的空间中进行SVM。另外，通过IKPCA 阶段的降维，可以很好地处理高维数据中的信息冗余，并且也一定程度地缓解了样本稀疏的问题。基于该结论，设计出求解IKSVM 问题的新型学习框架TP-IKSVM，具体算法的描述如下：

输入：K，不定核矩阵；Y，类别标签；p1+q1，IKPCA 所要降到的维度；λ，规则化参数；k(·,x*)，所有训练样本与测试样本x*核相似性度量。

输出：y*，x*的预测标签。

（1）利用式（4）计算Q，并保留对应特征值前(p1+q1)大的特征向量。

（4）计算x*的低维映射特征。

4 实验及结果分析

本章通过在两种数据类型向量形式的数据、结构化的数据上的实验，检验所提TP-IKSVM 算法的性能。实验选择如下主流IKSVM 方法作为对比算法：

（1）1-normIKSVM[7]：通过特征空间的嵌入，将IKSVM 问题转化成线性规划问题进行求解。

（2）ESVM[12]：首先求解相应的正定核支持向量机问题，然后通过映射矩阵P将KSVM 的解映射到IKSVM 问题的解。

（3）IKSVM-DC[14]：通过非凸优化算法——凸差规划进行求解。

（4）Kreĭn[15]：将IKSVM 的学习问题转化成带约束的特征值问题进行求解。

4.1 向量形式的数据集上的实验

本组实验采用6个向量形式的高维数据集（http://featureselection.asu.edu/datasets.php）:Leukemia、ALLAML、Colon、Prostate_GE、TOX_171 和CLL_SUB_111_2，数据集的详细统计信息如表1 所示。

Table 1 Description of 6 vectorial datasets表1 6 个向量形式的数据集描述

由于本组实验数据集是向量形式的样本，因此这里需要手动构造不定核矩阵。这里选用最常用的“sigmoid”核作为相似性度量核函数：

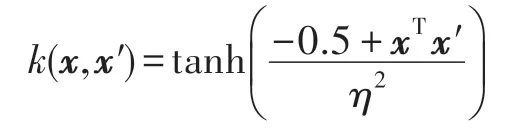
其中，核参数η的设置参照文献[15]的选取方式，即:

本组的TOX_171 数据集是一个四分类问题，而IKSVM 本身是处理二分类问题的技术，因此本节将类别标签为1、2 的样本作为正例样本，标签为3、4 的作为负例样本。相关参数的取值范围设置为C∈{20,21,…,26},λ∈{2-6,2-5,…,26}。将数据集随机划分为数量大致相等的训练数据集和测试数据集，并且进行10 轮的随机划分，实验结果取自10 轮实验的平均值。实验结果见表2。

由表2 可知，本文算法在本组数据集上的分类精度性能均优于其他对比算法，并且算法执行速度和1-normIKSVM、Kreĭn 大致相当。本组实验的数据集样本数量较少而特征维度较大，并且包含较多冗余信息，使得现有IKSVM 算法的性能表现不佳。而TP-IKSVM 通过两阶段的学习框架，能够充分发挥IKPCA 在处理高维数据方面的优势，使得数据的冗余信息得到削弱。同时，经过IKPCA 的操作使得样本点分布在一个较低维的空间，使得样本稀疏问题得到了一定程度的缓解，从而使得本文算法的性能得到进一步提升。

4.2 结构化的数据集上的实验

本节实验数据集是由代尔夫特理工大学模式识别实验提供的给定不定性度量矩阵[18]的结构化数据，并且本组数据集主要涉及生物信息和计算机视觉等领域的高维特征度量问题。数据集的详细统计信息见表3。

Table 2 Performance comparison of vectorial datasets表2 向量形式的数据集性能对比

Table 3 Description of 7 structured datasets表3 7 个结构化数据集描述

通过表3 的描述可知，本组数据集包含多分类问题，因此需要将多分类问题改为二分类问题，本文参照文献[14]的设置方式，即选取一半的类别标签作为正类，余下类别标签作为负类。比如将DelftGestures数据集中标签为1～10 的样本作为正类，11～20 的作为负类。其余相关参数设置同4.1 节。将核矩阵随机选取一半的行及相应的列所组成的子矩阵作为训练数据集，用余下列与之前选取的行所组成的子矩阵构成测试数据集，并将数据集随机进行10 轮划分，并取10 轮实验结果平均值作为最终的结果度量。实验结果见表4。

从表4 可以看出，TP-IKSVM 算法的分类精度优于所有对比算法，Kreĭn 算法次优，并且本文算法的运行速度明显高于IKSVM-DC。在Zongker、Catcortex 和Chickenpieces数据集上的分类精度分别提高了4.5%、4.1%和14.9%左右。分析可知Zongker、Catcortex和Chickenpieces等数据集所提供的数据可能包含较多的冗余或者噪声信息，使得普通的IKSVM 算法性能受限，而TP-IKSVM 通过将IKSVM 问题拆分为IKPCA 和SVM 两个阶段进行，使得信息冗余问题得到缓解，进一步使模型精度得到改善。同时，本组实验也验证了本文所提模型不仅在处理高维数据本身的冗余信息时有效，在处理由核的引入而导致的潜在高维特征空间中的信息冗余和样本稀疏问题仍然有效。

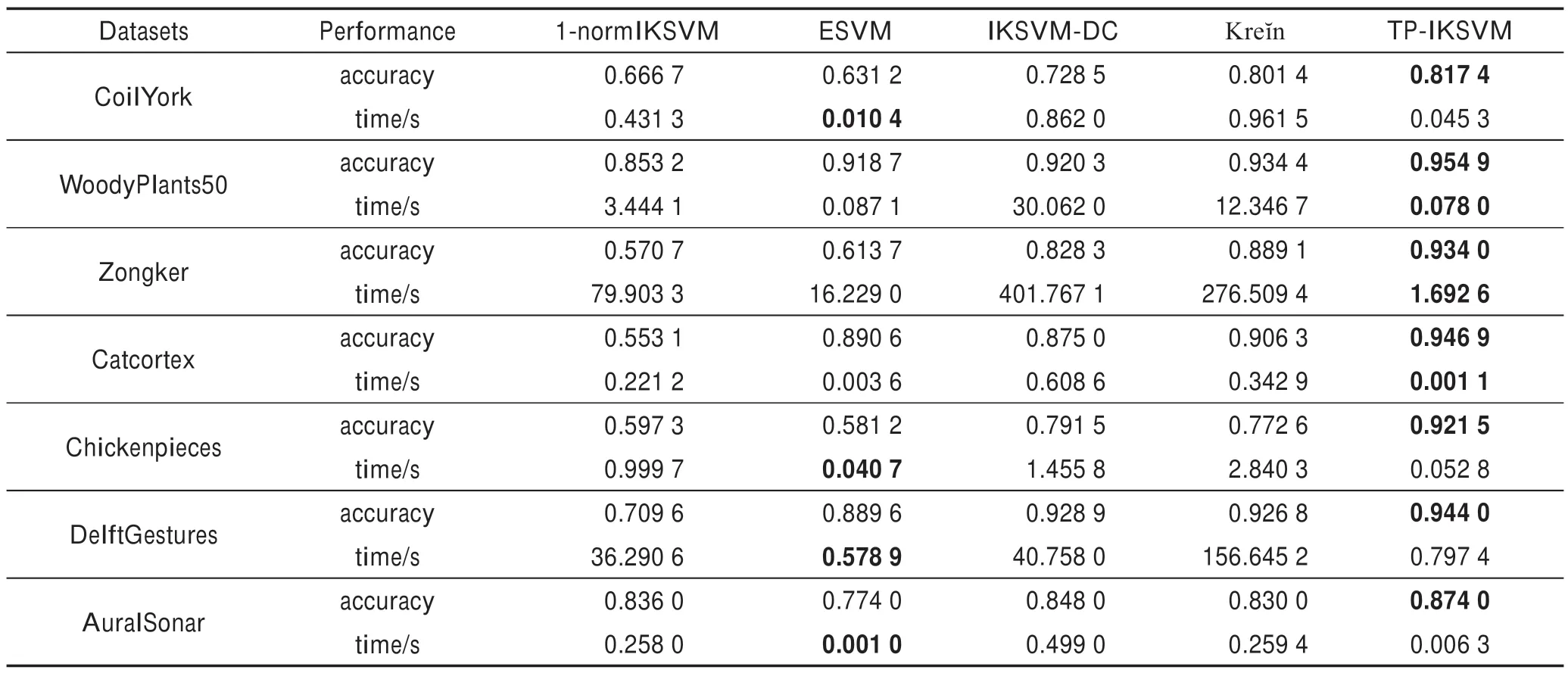
Table 4 Performance comparison of structured datasets表4 结构化数据集性能对比

5 结束语

鉴于现有IKSVM 算法无法较好地处理高维数据的研究现状，本文首先基于RKKS 中对IKSVM 的稳定化问题的定义，证明了IKSVM 问题的求解可以等价为IKPCA 和SVM 的依次执行，并且进一步提出了一种求解IKSVM 问题的新型学习框架TP-IKSVM。TP-IKSVM 将IKSVM 问题的求解分解为IKPCA 和SVM 两个阶段。TP-IKSVM 不仅发挥了SVM 在分类问题上良好泛化性能的优势，而且结合了IKPCA在处理高维数据方面的降低冗余信息和缓解样本稀疏的优势。最后，真实数据集上的实验验证了本文所提算法能够有效改善IKSVM 的实际泛化性能。