灰狼优化的混合参数多分类孪生支持向量机*

周广悦，李克文，刘文英，苏兆鑫

中国石油大学（华东）计算机科学与技术学院，山东 青岛 266580

1 引言

孪生支持向量机（twin support vector machine，TWSVM）是由Jayadeva 等人[1]在支持向量机的基础上提出来的一种新型的机器学习算法，通过为每一类样本构造一个超平面，使得该超平面距离本类样本最近，同时远离另一类的样本，进而解决二分类问题。但在现实问题中，多分类问题普遍，研究多分类问题变得更加有意义。

目前构建多分类支持向量机的方法分为两种：一种是直接法，通过修改目标函数，将多个分类面的参数求解合并到一个优化问题中，这种方法看起来简单，但计算复杂度很高，比较适合求解小型问题。另一种是间接法，通过不同的组合策略将多个二分类器构造成多分类器，该方法容易理解，较为常用。于是许多专家学者采用间接法，在构建多分类孪生支持向量机的领域做了大量研究：Xie 等人[2]提出了一对多孪生支持向量机，通过采用“One-versus-All”构建方法将二类孪生支持向量机扩展到多类。Shao等人[3]表明“One-versus-One”多分类策略与标准TWSVM 相结合，得到的一对一孪生支持向量机性能要好于OVATWSVM（one-versus-all twin support vector machine）。除了以上两种常用于构建多分类器的方法，Ding 等人[4]还根据多分类孪生支持向量机子分类器的组织结构，将它们分为基于“一对余”“二叉树”“多对一”“有向无环图”策略等一系列多分类孪生支持向量机。为了进一步提升多分类器的分类性能，学者们针对单个二分类孪生支持向量机的结构进行了不少改进[5-9]，但无论是标准孪生支持向量机还是改进的孪生支持向量机都面临着参数选择的问题。孪生支持向量机的性能主要取决于核参数以及惩罚参数的选择，参数选择的好坏将对分类性能产生直接的影响。除此之外，一个好的参数选择将直接提升孪生支持向量机的性能。目前孪生支持向量机的参数根据经验在一定范围内随机选取，具有很大的随意性和盲目性。许多专家学者对参数选择进行了大量的研究：Ding 等人[10]提出了一种基于粒子群优化算法的孪生支持向量机（twin support vector machines based on particle swarm optimization），该算法采用粒子群优化孪生支持向量机的惩罚因子，使其找到最优解。Zhang 等人[11]提出了一种基于果蝇优化算法的孪生支持向量机，果蝇优化算法由于其参数少，算法简单，能够快速找到惩罚因子以及核参数的最优解。Wu等人[12]提出了SFLA-MK-TWSVM（mixed kernel twin support vector machines based on shuffled frog leaping algorithm）方法，该方法通过采用蛙跳算法优化混合核函数孪生支持向量机，进一步提升了分类器的性能。Zhang等人[13]通过遗传算法优化的TWSVM 找到最佳特征，称为GATWSVM（twin support vector machines based on genetic algorithm），应用于飞机复合健康监测。

本文在“一对一”组合策略的基础上构建多分类孪生支持向量机，“一对一”方式通过在任意两类之间构建超平面，形成多个二分类器，最终通过投票的方式进行表决。各个二分类器在构建时采用的参数都是相同的，未考虑到不同类之间的差异性，本文提出了一种基于混合参数的多分类孪生支持向量机（multi-classification twin support vector machine based on mixed parameters，MP-MTWSVM），通过改进多分类器的构建方式，针对不同的二分类器采取不同的参数，能够保持各个二分类器的多样性，进而提升多分类器的性能。MP-MTWSVM 算法也引入了大量的参数，靠人工经验对每个二分类器进行参数设定，工作量大，且不能够准确选取能够提升该二分类器性能的参数，进一步提出了GWO-MP-MTWSVM（mixed parameter multi-classification twin support vector machine based on grey wolf optimizer），该方法使用灰狼算法对MP-MTWSVM 各子分类器进行参数优化，快速准确地找到最优参数组合。

2 相关算法描述

2.1 基于“一对一”策略的多分类孪生支持向量机

为了解决SVM（support vector machine）对大规模样本训练效率低的问题，2007 年，Jayadeva 等人在SVM 的基础上提出了孪生支持向量机（TWSVM）。与SVM 不同，TWSVM 构建两个超平面，使得每一个超平面距离一类样本尽可能得近，距离另一类的样本尽可能得远。TWSVM 通过求解两个二次规划问题QPP（quadratic programming problem）寻找超平面，不仅保持了SVM 的优点，而且训练速度是SVM 的1/4[14]。因TWSVM 最初是为了解决二分类问题而提出来的，因此需要结合额外的多分类扩展策略才能用于解决多分类问题。“一对一（one-versus-one，OVO）”扩展策略作为常用方法之一，其原理是在任意两类之间构建一个二分类TWSVM，则K个类别就需要设计K(K-1)/2 个二分类TWSVM，该方法一般采用“投票法”进行类别的判断。“投票法”在决定待分类样本的归属时，依次用一对一多分类孪生支持向量机（OVO TWSVM）的各个二类分类器进行判别，如果i、j两类间的分类函数将给定样本分到i类，则该二分类器将“票”投给了i类，否则j类得到该票，当遍历完所有的二分类TWSVM 后，给定样本将被分到“票数”最高的那个类。OVO TWSVM 的基本原理如下：

对于线性可分的情况，在任意i、j两类样本之间构建二分类TWSVM[1]，得到如下两个超平面：

对于非线性可分的情况，通过引入核函数K，TWSVM 的两个超平面如下所示：

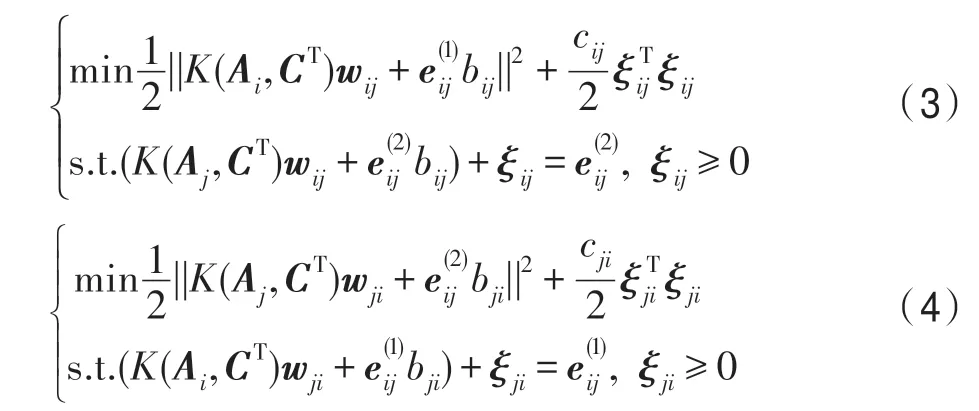
其中，cij和cji是两个惩罚参数，是两个全由1组成的列向量，ξij、ξji是松弛变量。

通过求解式（3）、式（4）的对偶问题，得到超平面的参数，构建OVOTWSVM 分类器，最终通过“投票法”对新样本进行类别标签预测。

2.2 灰狼优化算法

灰狼优化算法（grey wolf optimizer，GWO）是2014 年由Mirjalili 等人[15]提出的一种智能优化算法，该算法原理简单，需要调整的参数少，易于实现，全局搜索能力强。引起了国内外学者们的广泛关注，对GWO 进行了大量的研究：Emary 等人[16]采用多目标灰狼优化算法进行特征选择，通过GWO 搜索特征空间，找到最优的特征子集。Elhariri 等人[17]提出采用GWO 优化支持向量机SVM 的参数，实验结果表明，GWO-SVM 相对于SVM 有更好的分类精度。Heidari 等人[18]将Levy flight 和贪婪选择策略与改进的狩猎阶段相结合，提高了GWO的效率。Zhu等人[19]结合灰狼优化与差分进化算法，提出了HGWO（hybridizing grey wolf optimization with differential evolution）算法，该方法加快了GWO 的收敛速度，在优化性能与探测方法方面更有优势。Wei 等人[20]通过适应度值控制灰狼个体的位置，实现灰狼优化算法的自适应搜索，从而加快了收敛速度，避免陷入局部最优。

灰狼优化算法主要是根据灰狼群体捕食行为提出的，通过狼群追踪、包围、追捕、攻击猎物等过程来达到优化搜索的目的。它们之间具有严格的等级制度如图1 所示。

α、β、δ、ω代表不同等级的灰狼，且支配率自上而下下降。为了对灰狼的社会制度进行数学建模，将α作为最优解，β、δ分别作为次优解及第三优解，它们领导其他狼朝向猎物可能的位置。ω代表其余解，它们根据α、β、δ进行位置更新。下面介绍算法中的三个关键点[15]。

Fig.1 Hierarchy of grey wolf图1 灰狼等级

（1）灰狼与猎物的距离

计算机检索 Cochrane图书馆、PubMed、Embase、Medline、中国知网、维普数据库、中国生物医学文献数据库和万方数据库等。中文检索词为“前列腺素类似物”“青光眼”“角膜厚度”等；英文检索词为“Prostaglandin analogues”“Glaucoma”“Corneal thickness”等。检索时限均为2008年1月1日至2018年1月1日。

其中，D表示灰狼与猎物的距离，t表示当前的迭代次数，C表示系数向量，XP表示猎物的位置，X(t)表示灰狼目前所在的位置。

其中，r1是[0，1]之间的随机向量，C为猎物提供随机权重，通过随机加强(|C|＞1)或减弱(|C|＜1)猎物与灰狼之间的距离探测和开采搜索空间。

（2）灰狼位置更新

其中，X(t+1)表示更新后的灰狼位置，A表示系数向量，a从2 逐渐减少到0，r2是[0，1]之间的随机向量，随着A的减少，一半的迭代用于探测(|A|＞1)，其余的迭代用于开采(|A|＜1)。

（3）猎物位置定位

在抽象的搜索空间中，并不知道猎物(最优解)的具体位置。根据灰狼的等级制度，狩猎通常由灰狼α、β、δ引导，于是假设α(最优候选解)、β(次优候选解)、δ(第三优候选解)对猎物的位置有更好的了解。已知灰狼α、β、δ最靠近猎物，通过保存每次迭代过程中获得的三个最优解α、β、δ，猎物的方位可以根据这三个最优解的位置来确定，并迫使其他灰狼个体根据这三个最优解的位置更新其位置。灰狼个体跟踪猎物方位的数学描述如下：

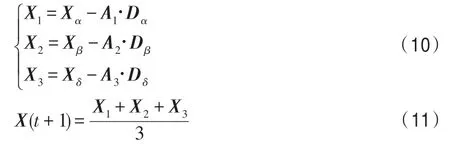
由式（9）、式（10）计算灰狼个体与α、β和δ的距离，然后由式(11)综合判断出灰狼个体向猎物移动的方向。其中，Dα、Dβ、Dδ分别表示灰狼个体与灰狼α、β、δ之间的距离，Xα、Xβ、Xδ分别表示灰狼α、β、δ的位置，A1、A2、A3是系数向量，C1、C2、C3是随机向量，X是当前灰狼个体的位置。

3 基于灰狼优化的混合参数多分类孪生支持向量机

3.1 基于混合参数的多分类孪生支持向量机设计

孪生支持向量机的性能在很大程度上受参数选择的影响，好的参数会直接提升分类器的性能，TWSVM 主要考虑的参数包括两种：一种是核参数；另一种是误差惩罚参数。对于核参数，基于本文实验采用的核函数是高斯径向基，于是核参数就是δ，δ参数的改变导致TWSVM 向高维度投影的特征空间的复杂度改变。如果δ值较大，特征空间的复杂度较低，线性可分性较差；如果δ值趋向于0，特征空间的复杂度趋向无穷，此时可将任意数据线性可分，但往往会造成过拟合[21]。对于误差惩罚参数，其表示对误差的容忍程度，惩罚参数越大，说明对误差的容忍程度越小，容易过拟合；惩罚参数越小，说明对误差的容忍程度越大，容易欠拟合[22]。因此如何选择合适的核参数及惩罚参数对于TWSVM 的分类效果及泛化性能来说是非常重要的。

本文采用“一对一”策略将二类孪生支持向量机扩展到多分类孪生支持向量机（multi-classification twin support vector machine，MTWSVM），但MTWSVM中的各个子分类器都采用相同的惩罚参数以及核参数，忽略了不同子分类器之间的差异。在相同的参数下，很难同时提高每个子分类器的性能，这限制了MTWSVM 整体性能的提高。于是提出一种基于混合参数的多分类孪生支持向量机（MP-MTWSVM），通过对不同的子分类器选取合适的参数，保证分类器的多样性，进而根据“一对一”策略构建多分类孪生支持向量机。

3.2 基于灰狼优化的混合参数多分类孪生支持向量机模型

MP-MTWSVM 提高了TWSVM 分类性能，同时也增加了大量的参数。由于参数增加了，使得算法的复杂性增加，孪生支持向量机本就面临着参数难确定的问题[12]，因此必须在使用混合参数提升分类性能的同时解决参数选择的问题。因此本文进一步提出了基于灰狼优化的混合参数多分类孪生支持向量机（GWO-MP-MTWSVM）。灰狼优化算法（GWO）具有结构简单，易实现，全局性能好的优势，通过灰狼算法对MP-MTWSVM 进行参数优化，不仅能够找到比传统优化方法确定参数更好的参数值，还能够在一定程度上缩短运行时间，提高算法的分类准确率。

已知在灰狼优化算法中，灰狼个体的位置代表需要优化问题的潜在解，在本文提出的GWO-MPMTWSVM 中，要被优化的问题就是组成MTWSVM的每个二类TWSVM 的分类准确率，分类准确率越高越好，潜在解就是使得每个二类TWSVM 分类准确率最高时选择的惩罚参数cij、cji以及核参数δij，其中i,j表示任意两类样本的类号。假设需要分类的类别个数为m，根据OVO 策略需要训练的二分类TWSVM的个数为m(m-1)/2，为每个二分类器分配一个编号r，则灰狼个体的位置向量表示为：

其中，r=1,2,…,m(m-1)/2 表示二类TWSVM 的编号，cr,1、cr,2分别表示第r个二类TWSVM 对应的惩罚参数，δr表示第r个二类TWSVM 对应的核参数，Fr表示第r个二类TWSVM 的适应度值。

GWO-MP-MTWSVM 的训练步骤描述如下：

（1）导入数据集，按6∶4 将数据集随机划分成训练集与测试集。

（2）初始化灰狼种群，随机产生n个体的位置向量，并初始化a、A、C、Xa、Xβ、Xδ的值。

（3）对于k=1,2,…,n，将第k个灰狼个体位置向量中cr,1、cr,2、δr赋值给第r个二类TWSVM 的惩罚参数及核参数，对训练数据集进行分类，计算该二类TWSVM 的分类准确率作为适应度值Fr。

（4）将n个灰狼个体各二类TWSVM 的适应度值与Xα、Xβ、Xδ各二类TWSVM 的适应度值作比较，记录每个二类TWSVM 分类准确率最高的三组参数对，确定当前的优解Xα、次优解Xβ和第三优解Xδ。

（5）计算a、A、C的值。

（6）根据式（11），更新当前个体的位置。

（7）判断迭代次数是否已经达到了初始化的最大迭代次数，如果达到了，则继续执行（8）；否则迭代次数加1，然后转到（3）。

（8）将得到的最优解Xα的值赋值给各个二类TWSVM 的惩罚参数及核参数。

（9）将训练好的m(m-1)/2 个二类TWSVM 组合成一个多类MTWSVM，根据“投票法”进行类别决策。

为了更直观地描述算法，绘制了算法流程图，如图2 所示。

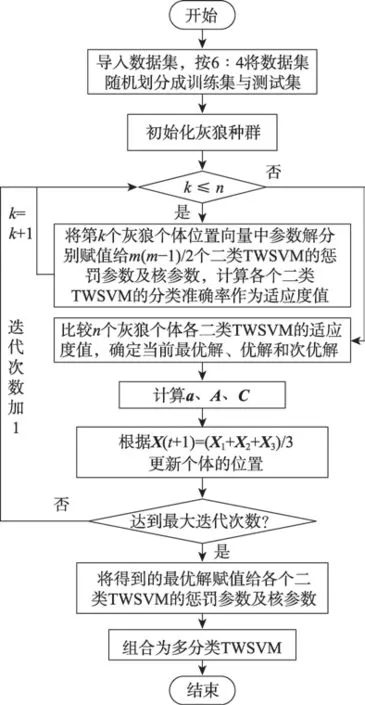
Fig.2 Flow chart of GWO-MP-MTWSVM图2 GWO-MP-MTWSVM 的算法流程图

4 实验与分析

本实验选用了UCI 数据库中的8 个公开数据集，随机选取其中的60%用于训练，剩下的40%作为测试。这些实验均在PC 机（4 GB 内存，903 GB 硬盘，CPU Intel i7-4790）上采用python 环境实现。本实验采用的8 个数据集的详细信息如表1 所示。

Table 1 Details of datasets used in experiments表1 用于实验的数据集的详细信息

在实验设置中，将灰狼算法的个体数量初始化为15，惩罚参数及核参数初始化为[0，10]之间的随机值，将孪生支持向量机的核函数设置为高斯核。表2列出了采用默认参数（惩罚参数设置为1，核参数设置为2）的多分类支持向量机（OVO SVM）、多分类孪生支持向量机（OVO TWSVM，惩罚参数cij、cji分别设置为1，核参数设置为2）、采用网格搜索优化参数的多分类孪生支持向量机（Grid-MTWSVM）、采用灰狼算法优化参数的多分类孪生支持向量机（GWOMTWSVM，以整体准确率作为适应度函数，各子分类器采用相同的惩罚参数及核参数）以及本文提出的GWO-MP-MTWSVM 算法之间在不同数据集上10次随机实验的平均分类准确率ACC、F1 值的对比。由表2 可知，GWO-MP-MTWSVM 算法无论是准确率ACC还是F1 值，在所有数据集上分类效果都是最佳的。其中，OVO TWSVM 在6 个数据集上的性能高于OVO SVM，证明了相对于SVM，TWSVM 不仅能够缩短运行时间，也能提高分类精度；Grid-MTWSVM在所有数据集上的性能都高于OVO TWSVM，证明了选择参数的重要性；GWO-MTWSVM 在所有数据集上的性能都高于Grid-MTWSVM，说明了GWO 算法具有良好的全局收敛性，因此GWO 找到的参数值比网格搜索要好。GWO-MP-MTWSVM 与GWOMTWSVM 都是通过灰狼优化算法寻找最优参数，GWO-MP-MTWSVM 在所有数据集上的性能都大于GWO-MTWSVM，证明了本文提出的GWO-MPMTWSVM算法的有效性。

因每次实验都是对数据集进行随机划分，为了进一步验证GWO-MP-MTWSVM 的有效性不局限于固定的数据分布，图3 展示了各对比算法在不同数据集上进行10 次随机实验的准确率对比。从图3 可得，对于Balance、Hayes 数据集，GWO-MP-MTWSVM 算法8 次准确率达到最优，其余2 次仅次于最优；对于Vehicle 数据集，GWO-MP-MTWSVM 算法9 次准确率达到最优，仅有1 次略低于最优；对于Iris、Seeds、Glass、Zoo、Landsat 数据集，GWO-MP-MTWSVM 算法10 次实验准确率全部达到最优。

Table 2 Comparison of classification performance among various algorithms on different datasets表2 各类算法在不同数据集上的分类性能对比

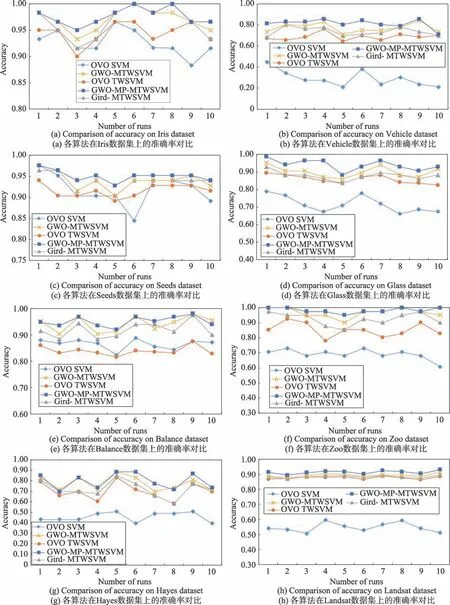
Fig.3 Comparison of accuracy among five methods on different datasets图3 五种算法在不同数据集上的准确率对比

由上可知，本文提出的GWO-MP-MTWSVM，采用基于混合参数的OVO 策略构建MTWSVM，通过对不同的子分类器选取合适的参数，充分发挥各子分类器的优势，同时利用GWO 简单、易收敛的优点找到算法的最佳参数组合，能够促进MTWSVM 的分类性能进一步提升。

5 结束语

近年来TWSVM 凭借其高效性得到了迅速发展，但将TWSVM 推广到多分类TWSVM 仍面临着巨大的挑战，目前在多分类TWSVM 构建过程中，各子分类器通常采用相同的惩罚参数及核参数，难以充分发挥各子分类器的有效性。本文首先提出了基于混合参数的多分类孪生支持向量机算法——MPMTWSVM，其考虑到不同子分类器之间的差异性，从而提高了MTWSVM 的性能；其次针对MPMTWSVM 参数难确定的问题，又提出了基于灰狼优化的混合参数多分类孪生支持向量机，GWO-MPMTWSVM 通过灰狼算法确定MP-MTWSVM 各子分类器的最优参数，进一步提高了MTWSVM 的性能。