有限空间的尘浓度分布规律数值模拟研究

徐陈又诗，张合，查冰婷，郑震，陈璟宜

(1.南京理工大学 智能弹药技术国防重点学科实验室，江苏 南京 210094；2.南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

激光探测具有高相干性、高定距精度、响应速度快、抗电磁干扰等优点，广泛应用于近炸引信[1-2]。自然环境中的尘及其他因素产生的高浓度扬尘，会使激光传输特性受到影响，导致激光引信的探测性能大幅下降甚至失效[3-5]。为揭示激光引信的探测性能与尘浓度的变化规律，设计并搭建有限空间内的尘实验室，研究空间内尘浓度分布，获得均匀尘实验平面，用以模拟真实战场尘浓度，变得尤为重要。

针对激光抗尘干扰实验的研究，国内外缺少尘浓度大小与激光抗尘能力之间的定量关系数据，原因在于无法得到均匀的尘浓度实验条件，都是通过向空间内输入定值的颗粒质量并持续地鼓风来间接描述环境浓度。南京理工大学建设有15.0 m×1.2 m×1.2 m大型简易尘实验靶道，通过将靶道分割成多段，每段同时进行独立实验，研究了不同颗粒直径、不同颗粒质量、不同风速对激光探测装置工作的影响及相应的尘沉降时间。由于未将风机鼓风口所在位置对实验靶道内气体与固体两相流的影响进行相应的数值模拟仿真，忽略了风机方位对尘颗粒运动的影响，导致实际的风机安装位置(安装在靶道侧面下方)无法通过持续的鼓风使鼓入的尘颗粒悬浮在空中，从而无法形成持续且一定浓度的尘干扰环境。同时由于实验靶道密闭的原因，无法进行自然风条件对颗粒沉降情况的实验研究。雷志勇等[6]通过建立边长为0.8 m的正方形尘实验箱，对平均尘浓度与激光传输特性开展研究。结果表明随着尘粒子平均浓度的不断增加，激光信号的透过率逐渐降低、衰减增大。由于受风速和箱体体积的限制，实验可测的浓度上限仅为5 g/m3，激光信号的衰减存在一个阈值，达到该阈值后激光信号的透过率基本保持不变。门俊儒[7]通过实验搭建了一个体积约为0.4 m3的尘颗粒实验箱，得到实验箱内尘浓度与激光接收装置经过光电转换输出电压之间的关系，通过理论分析，将电压转化为对应的透过率。由于实验箱内的尘颗粒随气流不断地做涡旋运动，导致箱体内各部分的颗粒浓度分布不均，文献[6-7]并没有得出激光传输特性与准确浓度之间的定量关系，而是采用了平均浓度(颗粒总质量除以箱体体积)代替准确浓度。程卫民等[8]和孙彪等[9]基于综合机械化采煤工作面风流场和颗粒流场特点，采用数值模拟方法研究了综采面在不同风速下的扩散作用，以及滚筒旋流风对截割煤尘侧向逸散的规律。徐世凡[10]通过数值模拟对烟尘浓度空间分布规律进行了研究。陈慧敏等[11]通过数值模拟研究，得到了单辆坦克不同行驶速度对扬尘浓度分布的影响规律。Yao等[12]通过模拟研究沙尘天气下的激光衰减特性，发现激光衰减随大气能见度的增加而减小。在我国国家军用标准GJB 282.3—91装甲车辆环境条件砂尘极值[13]和GJB 1171—91 军用直升机防砂尘要求[14]中，装甲车辆编队在砂土路上行驶产生的最大扬尘浓度为2 g/m3，军用直升机在沙漠中起降期间产生的最大扬尘浓度为10 g/m3.

针对现有实验设备无法形成一定浓度且持续的尘实验平面，导致无法得到激光传输特性与准确浓度之间的定量关系且实验得到尘浓度范围偏小的问题，本文采用计算流体力学(CFD)数值模拟法，基于ANSYS ICEM和Fluent软件对2 m×1 m×1 m有限空间内的尘浓度分布规律进行研究，形成一定均匀浓度的尘浓度分布面；建立质量流率与尘浓度、速度与尘浓度之间的数学关系，分析质量流率与速度对尘浓度的影响，最终要求能够形成的尘平面浓度在0.1～20.0 g/m3范围之间可控。

1 仿真模型的确定

1.1 数学模型

1.1.1 湍流模型

流体的流动可分为层流和湍流。层流是指当雷诺数较小时，流体中层与层之间相互没有干扰，没有质量和动量传递的分层流动；湍流是指当雷诺数较大时，流体中层与层之间相互干扰、混合，质量和动量相互传递，处于一种高度复杂的、不规则的流动[15]。雷诺数定义为

(1)

式中：v为入口截面的流体平均速度；ω为流体的运动黏度；dw为水力直径，

(2)

A为过流断面的面积，S为过流断面的周长。

有限空间内尘浓度的计算选取标准k-ε模型，k为湍流动能(m2/s)，ε为湍流动能耗散率(m2/s3)。此模型具有一定的计算精度且计算量较小，多用于计算复杂的湍流流动，它与单方程的差别在于引入了耗散率ε，与湍流动能k相结合[16]。

湍流脉动动能方程(k方程)和耗散率方程(ε方程)分别如下：

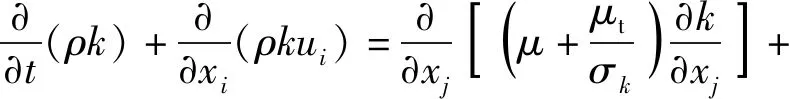
(3)

(4)

式中：ρ为气体密度(kg/m3)；xi、xj为坐标(m)，i≠j；ui、uj为不同坐标点处的流体速度(m/s)，i≠j；μ为层流的黏性系数(Pa·s)；μt为湍流黏性系数(Pa·s)；σε、σk分别为湍动能耗散率ε和湍流动能k对应的普朗特数，σε=1.3，σk=1.0；Gk为由层流速度梯度产生的湍动能(m2/s2)；Gb为由浮力产生的湍动能(m2/s2)；YM为可压缩湍流中由过度扩散产生的波动；Sk、Sε为定义的湍流动能；C1ε、C2ε、C3ε为经验常数，C1ε=1.44，C2ε=1.92，C3ε=1.

1.1.2 离散项模型

尘在空气中的运动属于气体与固体两相流，目前研究气体与固体两相流的物理模型有连续介质模型、离散颗粒模型和流体拟颗粒模型。尘实验室中离散相颗粒体积占比小于10%，故采用离散颗粒模型，该模型将气体相视为连续相，将颗粒相视为离散相，考虑了颗粒与气体间、颗粒与颗粒间的相互作用遵循欧拉- 拉格朗日方程[17-18]。

颗粒所受作用力平衡方程如下：

(5)

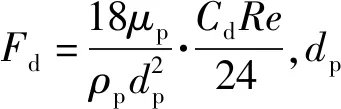
真实环境中的尘分布规律复杂多变，为了方便建立数学模型，对复杂问题进行简化，对离散相模型作出如下假设：1)在流动过程中，流体为不可压缩流；2)离散相颗粒为粒径相同、密度均匀的球体；3)气体与固体两相流具有相同的温度场；4)不考虑离散相颗粒与壁面的摩擦力。

1.2 物理模型

以长×宽×高分别为2 m×1 m×1 m的立方体作为物理原型及计算域，结构及边界分布如图1、图2所示。模型z轴方向的z=0 m、z=1 m截面上开设有2个1.40 m×0.01 m的矩形鼓风口和2个1.00 m×0.01 m的矩形鼓料口，其中鼓料口位于鼓风口内且同轴对称，截面x=0 m和x=2 m上开设有同样规格为1.00 m×0.25 m的自然风口和出口。

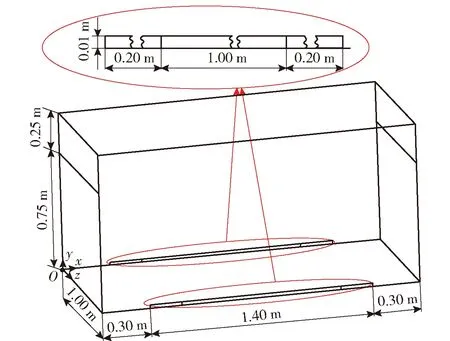
图1 尘场结构示意图Fig.1 Schematic diagram of dust field structure

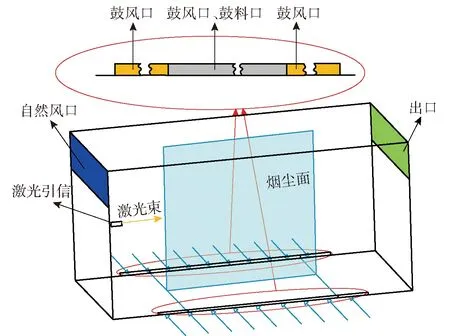
图2 尘场边界定义图Fig.2 Boundary definition diagram of dust field

针对结构规则的立方体计算域，采用ICEM CFD软件进行六面体结构网格划分。结构网格能够很容易地实现区域的边界拟合，网格生成速度快且质量高，从而能够显著加快收敛速度。由于相对面积较小的鼓风口和鼓料口需对网格进行加密处理，远离鼓风口和鼓料口的网格可以采用Geometric节点分布律对其进行适当变疏处理，以减少计算量，最终网格数量为90万，网格质量全都优于95.8%，保证了求解的精度及收敛性。

2 仿真条件

将ICEM CFD软件建成的物理模型和网格导入Fluent软件中，修改相应数学模型的有关参数，并对物理模型边界条件和离散相(颗粒)参数进行设置，如表1所示。

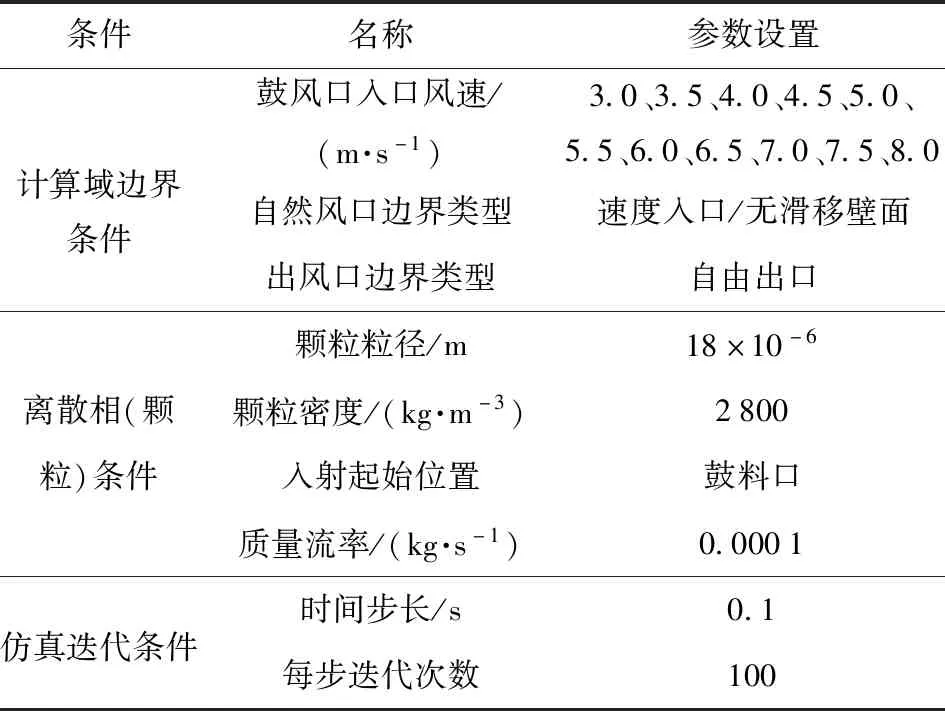
表1 仿真条件设置Tab.1 Setup of simulation conditions

3 仿真结果与分析

设置鼓风口风速为4 m/s，通过(1)式、(2)式计算水力直径dw为0.036 m，湍流强度为5.088%.实验室尘浓度分布云图如图3(a)、图3(b)所示。设置图例最大浓度值为0.003 kg/m3用以观察比较云图分布情况，得到x=1.0 m截面和z=0.5 m截面4个特征时间节点，分别为t=0.4 s、t=0.8 s、t=1.2 s、t=1.6 s的尘浓度分布情况。

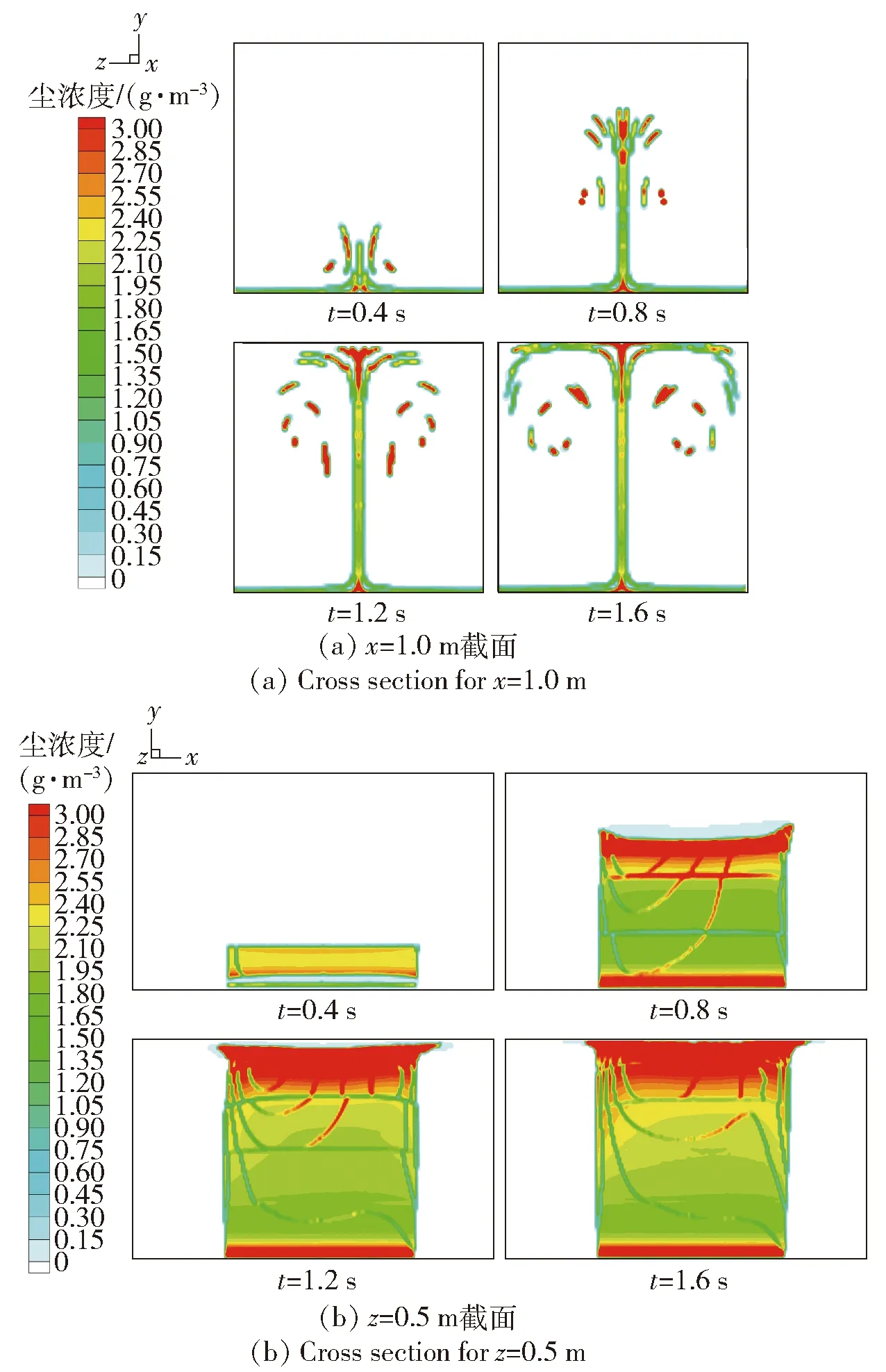
图3 不同截面尘浓度分布云图Fig.3 Graphics of dust concentration distribution on different cross sections

分析可得：颗粒在速度4 m/s的风吹动下，由z=0 m和z=1 m两个截面上的鼓料口进入尘实验室，于z=0.5 m截面汇聚后向y轴正方向扩散。为防止颗粒在z=0.5 m截面向x轴两侧扩散形成高浓度颗粒束而影响实际探测的准确性，鼓风口长度相对于鼓料口两侧各长0.2 m，从而将尘面的长度控制在1 m.当t=0.4 s时，形成的尘高度为0.276 m，浓度范围2.25～2.40 g/m3.当t=0.8 s时，在两侧鼓风口的风相互作用下，颗粒逐渐向y轴正方向扩散，尘高度为0.776 m.当t=1.2 s时，形成的尘面浓度分多个层次，除鼓料口处浓度高外，浓度随尘高度的升高而增大。随着时间不断推移，由于颗粒不断向上方聚集，受自身重力影响及不断减小的升力作用，尘向上的趋势相对于前一时刻不断减小。当t=1.6 s时，在整个尘场中部偏下形成一段0.2 m×1.0 m较为均匀的尘浓度面，选取为尘实验面，浓度范围为1.95～2.10 g/m3.图3中均匀尘浓度面存在几条浓度较低的颗粒束，故可忽略其对均匀平面的影响。

3.1 不同质量流率下尘颗粒浓度变化

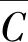
将数据图表化且进行曲线拟合，得到针对本文特定模型结构下的尘平均浓度与质量流率之间的相互关系，如图4所示。

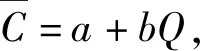
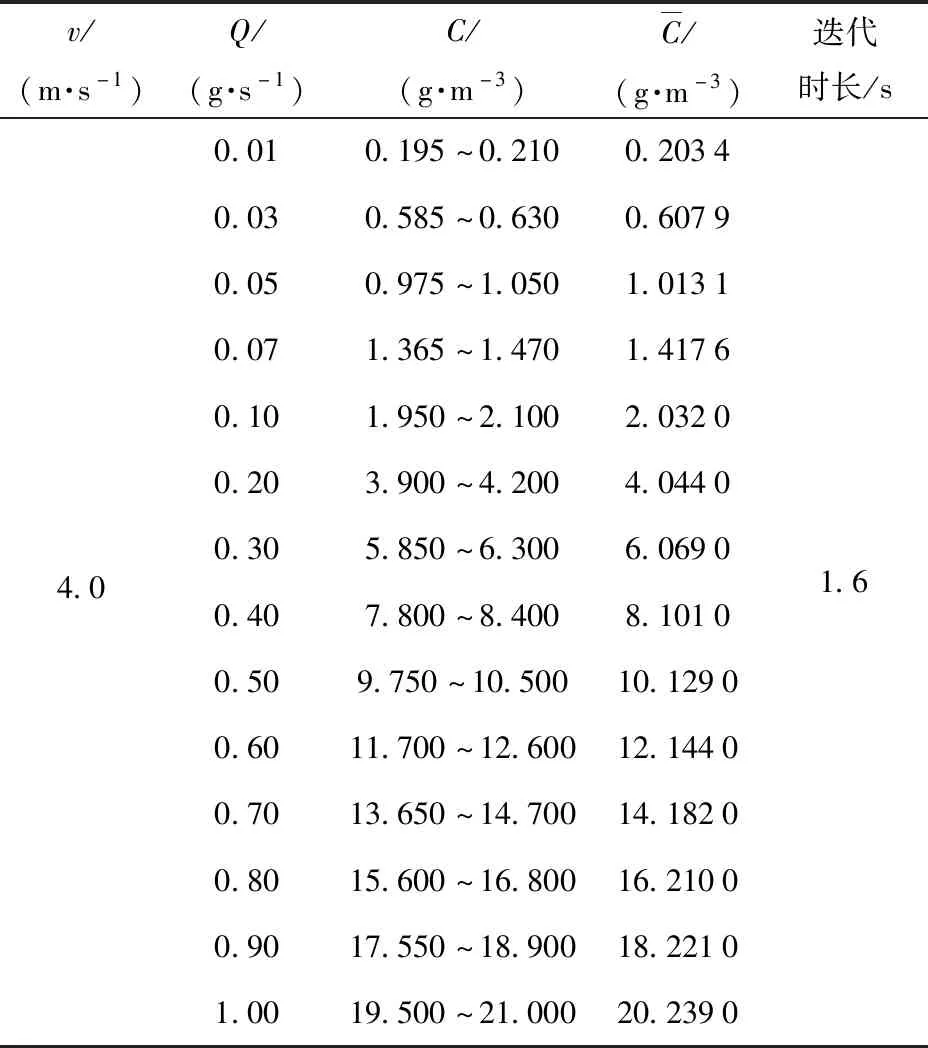
表2 尘平均浓度随质量流率变化Tab.2 Change of average dust concentration with mass flow rate

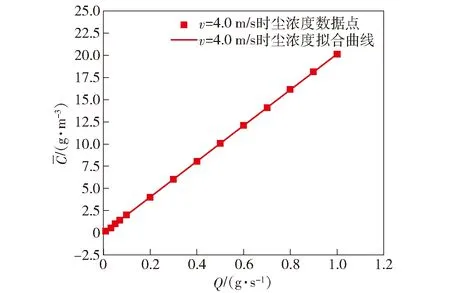
图4 尘浓度随质量流率的变化Fig.4 Change of dust concentration with mass flow rate

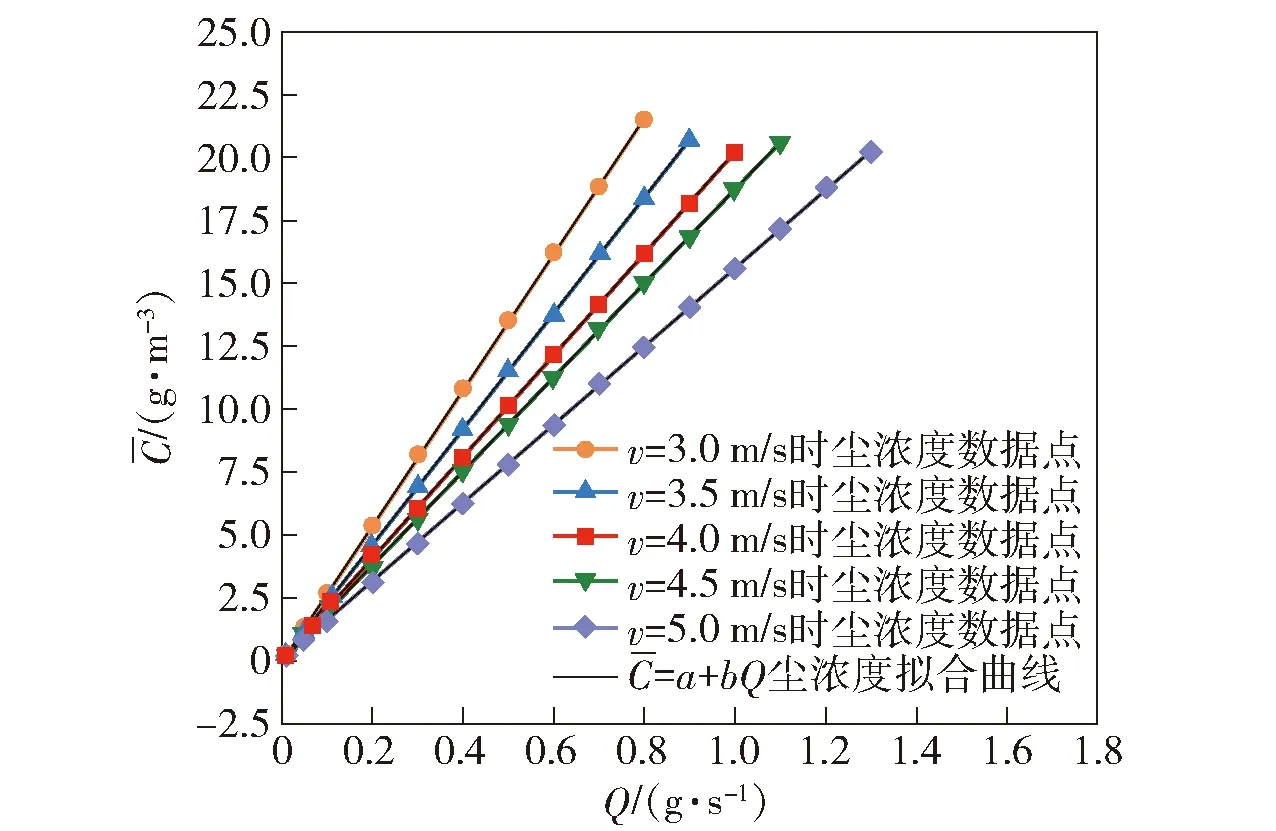
图5 不同速度下尘浓度随质量流率的变化Fig.5 Change of dust concentration with mass flow rate at different velocities of wind inlet

表3所示为曲线拟合参数表，根据图5曲线拟合结果，尘平均浓度与质量流量呈线性关系递增，质量流率越大，尘平均浓度越高。同一质量流率下，尘平均浓度随速度的增大而减小，表明随着风速的增加，颗粒所受升力越大，同一秒吹入相同质量的颗粒在风的作用下流动面积更大、速度更快，从而导致浓度变小。

3.2 不同风速下尘颗粒浓度变化

为分析同一质量流率下不同风速与尘平均浓度之间的关系，对模型做以下仿真：设置质量流率Q=0.50 g/s恒定，修改风速入口参数，直至出现均匀的尘浓度面时停止迭代，记录迭代时间和相关参数数据，如表4所示。

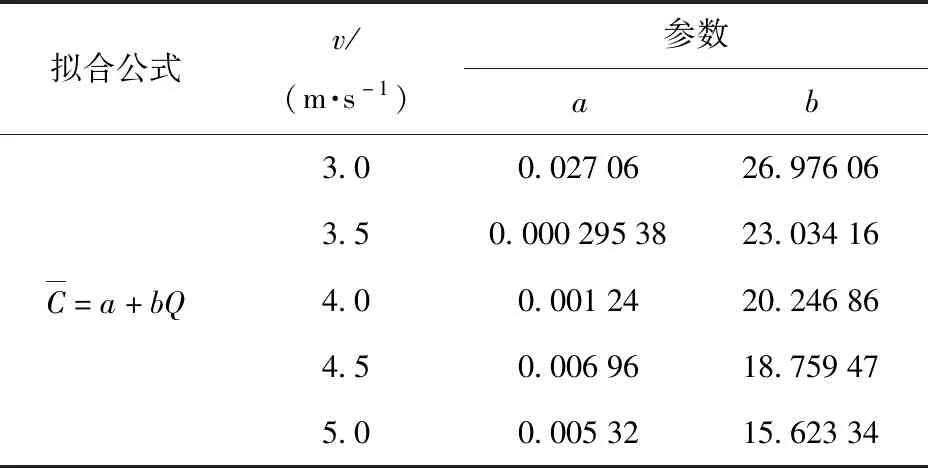
表3 曲线拟合参数Tab.3 Curve fitting parameters

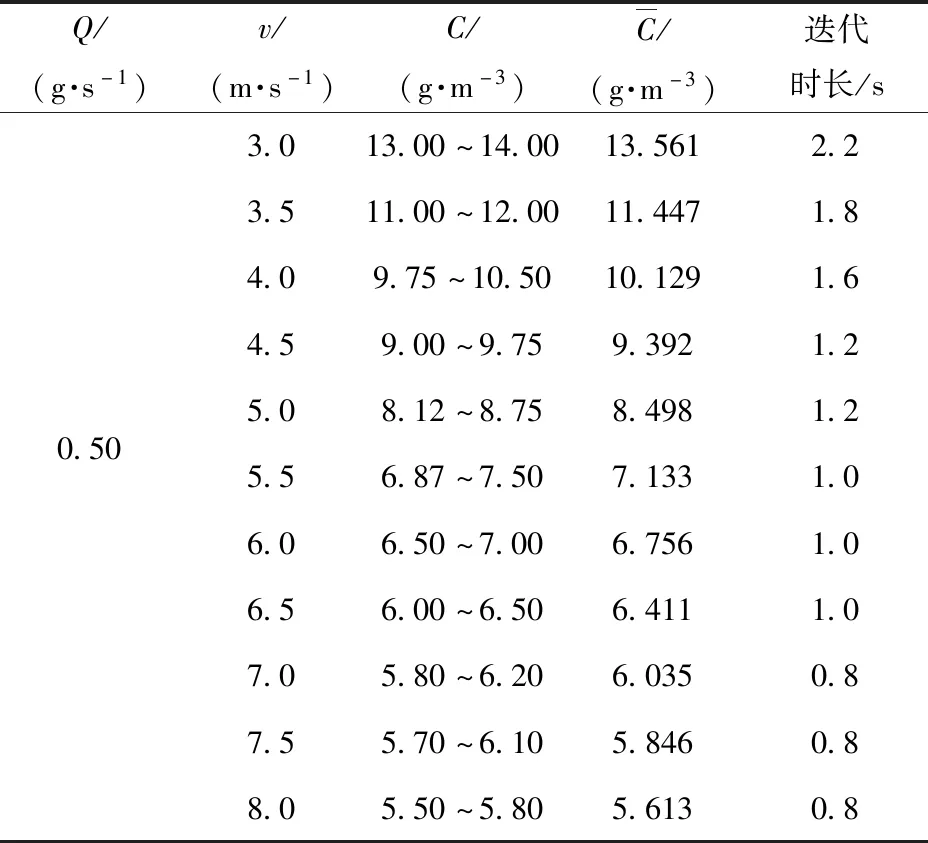
表4 尘平均浓度随速度的变化Tab.4 Change of dust concentration with velocity of wind inlet

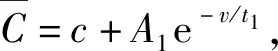
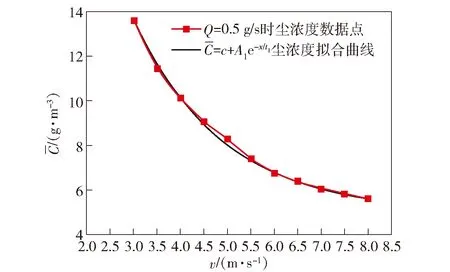
图6 尘浓度拟合曲线Fig.6 Fitting curves of average concentration of dust

3.3 自然风条件下尘的沉降时间

为研究环境中自然风对尘沉降速度的影响，对形成的特定尘面在无风及自然风情况下的沉降时间进行观察。

如表2所示，当鼓风口速度v=4.0 m/s、质量流率Q=0.10 g/s恒定、迭代时长为1.6 s时，形成的尘浓度面平均浓度为2.032 g/m3，对此状态下的尘平面以两种方案进行处理：1)更改鼓风口和鼓料口边界条件为壁面边界，离散相运动经壁面设置为反射，停止颗粒射入计算域，继续迭代至颗粒完全沉降(空间内漂浮颗粒浓度≤0.001 g/m3)停止，沉降过程耗时56 s，总时长为57.6 s；2)更改鼓风口和鼓料口边界条件为壁面边界，离散相运动经壁面设置为反射，设置自然风沉降入口为速度入口，速度为0.5 m/s，模型停止颗粒射入计算域，继续迭代至颗粒完全沉降(空间内漂浮颗粒浓度≤0.001 g/m3)停止，沉降过程耗时23 s，总时长为24.6 s.通过比较发现，颗粒在有自然风条件下的沉降时长比单重力作用沉降耗时少33 s，沉降速度作用明显。由此可见通过增设自然风口对实验后续的颗粒收集整理非常有益。

4 结论

1)采用Fluent软件对模型内的颗粒运动情况进行模拟仿真，在模型中间得到一个呈阶梯状分布的尘浓度平面，平面中间部分有一段浓度较均匀的截面，选取为尘实验面。通过改变鼓风口的进风速度及鼓料口的颗粒质量流率，调整尘实验面的浓度大小。研究结果表明：尘浓度与质量流量为线性递增关系，质量流率越大，尘浓度越高；尘浓度与速度呈指数关系衰减，速度越大，尘浓度越低，变化越缓慢。

2)实验室鼓风口风速可调节，在尘颗粒质量流率增加的同时增加风速，不仅能够扩展尘浓度范围至20 g/m3，还可以有效避免风速过低导致无法使尘颗粒保持悬浮，减少实际测试中激光信号由此产生的衰减阈值问题。

3)对自然风条件(自然风风速0.5 m/s)下的尘颗粒沉降情况进行模拟，结果表明自然风作用下的颗粒沉降时长比单重力作用耗时短33 s，可以有效加速颗粒沉降。模拟自然环境下颗粒随自然风的沉降作用，为建立战场中自然风速与尘浓度之间的关系，使激光引信有效地抗尘环境干扰、适时起爆战斗部、毁伤目标提供参考。

以上仿真方法和结论不仅适用于本文尘实验室设计方案，而且对于在不同规格大小的尘实验室中建立尘环境也具有一定的参考价值，可为不同波段激光在尘环境下的传输特性研究提供实验条件。