水声传感器网络信号到达时间差目标定位的最小二乘法估计性能
2020-04-16王领申晓红康玉柱花飞王海燕
王领,申晓红,康玉柱,花飞,王海燕,2
(1.西北工业大学 航海学院,陕西 西安 710072;2.陕西科技大学 电子信息与人工智能学院,陕西 西安 710021)
0 引言
在海洋环境监测中,分布式水声传感器网络是一种方便灵活的监测手段,目标定位是海洋环境监测的一个基本功能。国内外学者对基于多传感器节点的协同目标定位方法已开展了广泛研究[1-8]。常用协同目标定位方法的基本思想是:假设传感器网络各节点位置准确已知,每个节点获取观测值后,依据一定的定位算法提取其相关信息并传输至中心节点,中心节点依据获得的信息对声源位置进行估计[1-8]。其中,常用的基于测距的目标定位算法有基于信号到达时间算法、基于信号到达时间差(TDOA)算法、基于信号到达角度算法、基于到达频差算法、基于信号到达强度算法,以及以上算法的组合。由于基于TDOA的目标定位算法具有硬件要求低(每个节点仅需要有一个接收通道)、计算复杂度低、定位精度高等优点,是基于传感器网络节点对目标被动定位的首选算法[9-12]。在TDOA目标定位算法中,以Chan算法[13]、泰勒级数展开算法[14]和近似最大似然估计算法[15]的精度最高。特别是Chan算法采用基于两步加权最小二乘(WLS)算法给出了定位算法的解析解,并从理论和仿真两个角度证明当噪声较小且服从高斯分布时,其均方误差能达到克拉美罗下界(CRLB)[13]。由于性能优越,Chan算法得到了广泛应用。
目前研究的协同目标定位算法大多是针对陆地电磁波传感器节点的[1-13]。由于陆地传感器节点可借助于卫星使节点本身的位置误差较小,这些算法均假设传感器节点的位置准确已知,仅考虑对目标到达时间差的测量误差。水声传感器网络是以水声为通信介质,以海洋环境监测为目的,工作于水下,无法用卫星进行自定位,通常采用基于距离的传感器节点自定位。由于水声的非直线及长时延多径传播,使得水声节点的自定位误差远比基于卫星的自定位误差大(1个数量级以上)。此外,由于水中的浮标或潜标会随洋流飘动,在水声传感器网络对目标定位的算法中不能忽略节点的自定位误差,在这种情况下研究如何提高水声网络传感器节点对目标的协同定位精度,是十分迫切的。
本文针对水声传感器网络目标定位中节点位置误差和测距误差同时存在条件下的目标定位性能问题,建立双误差条件下的TDOA目标定位模型;提出一种基于加权整体最小二乘(WTLS)算法的TDOA目标定位算法,将测距误差和传感器节点位置误差的先验信息融入算法中。仿真结果表明,WTLS算法与常用的两步WLS算法相比,有很好的定位性能。
1 双误差条件下的TDOA目标定位模型
1.1 目标与传感器节点之间的几何关系
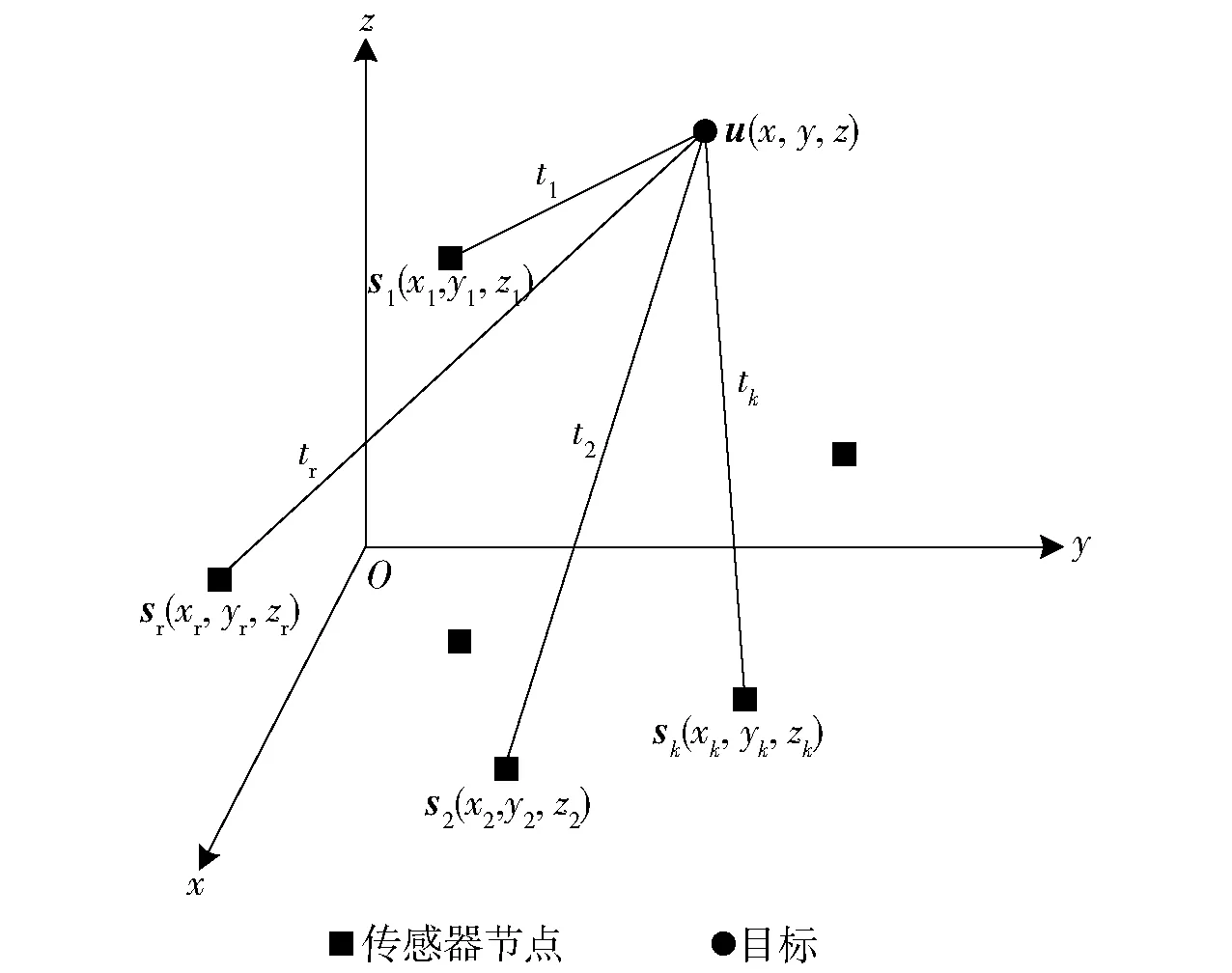
图1 基于TDOA的目标估计示意图Fig.1 Target estimation based on TDOA
基于传感器节点的目标定位示意图如图1所示。假设M个传感器节点的位置坐标分别为sk=[xk,yk,zk]T,k=1,2,…,M,xk、yk、zk表示第k个节点位置坐标的3个分量;单独将另一个传感器节点作为参考节点,用于计算目标到其他节点和到参考节点的距离差,参考节点位置坐标为sr=[xr,yr,zr]T,xr、yr、zr表示参考节点位置坐标的3个分量;目标位置坐标为u=[x,y,z]T。则第k个节点接收到目标u信号的到达时刻tk为
(1)
式中:c为水中声速,c≈1 500 m/s;t0为目标发射信号的时刻;nk为目标信号到达第k个传感器节点的时间估计误差,且独立同高斯分布。图1中,t1、t2、tk、tr分别表示第1个、第2个、第k个节点和参考节点接收到目标u信号的到达时刻。
当目标为非协作目标或异步网络时,目标的发射信号时刻t0无法获得,TDOA采用目标到节点与参考节点时间差的方法,无需知道目标发射信号的时刻t0.目标信号到第k个节点与参考节点的时间差为
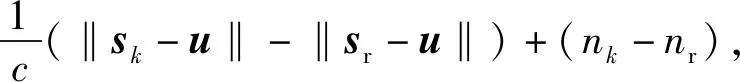
(2)
式中:nk、nr分别表示目标信号到达第k个传感器节点和参考节点的时间估计误差。对于三维目标定位,(2)式中的未知数u=[x,y,z]T的维数等于3,当M≥3时可得双曲方程(2)式的解;对于二维目标定位,(2)式中的未知数u=[x,y]T的维数等于2,当M≥2时可得双曲方程(2)式的解。此即基于TDOA的传感器节点目标定位思想。
(2)式的本质是求解由多个TDOA构成的双曲线的交点,当M取等号时得到三元二次方程(三维)或二元二次方程(二维),可直接求解;当传感器节点较多时,(2)式为超定非线性方程,不能直接应用线性方法求解,若采用迭代搜索法则存在收敛性问题。文献[16]提出一种参数变换的方法,通过二维坐标中目标、传感器节点之间的距离及其几何关系,利用一个中间未知量,将非线性方程转化为伪线性方程。文献[13]给出了含有目标位置坐标以及目标到参考节点距离的超定伪线性方程组,并采用两步WLS法给出该方程组的解析解。文献[13]采用二维坐标给出的结果也适用于三维坐标。本文借鉴文献[13]的思路,以二维坐标为例,所得结果同样也适用于三维坐标。
在二维平面中,目标到参考节点sr=[xr,yr]T的距离为
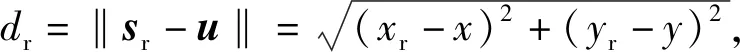
(3)
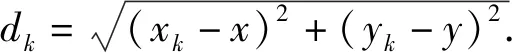
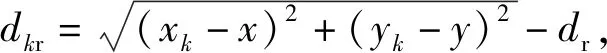
(4)
(4)式减去(3)式,得
(5)
式中:xkr=xk-xr;ykr=yk-yr.
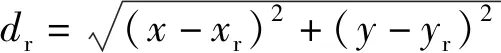
(6)
1.2 双误差条件下的TDOA目标定位模型
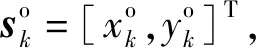
(Ga+ΔG)z=ha+Δh,
(7)
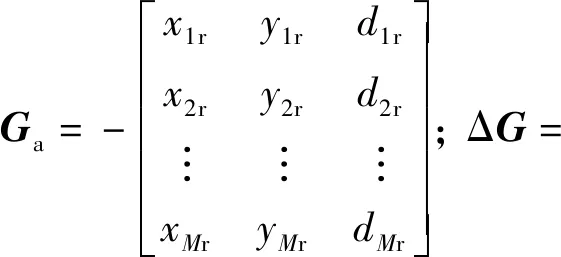

2 基于最小二乘的求解方法
高斯- 马尔可夫定理研究表明:在线性回归模型中,如果误差满足零均值、同方差且互不相关,则最小二乘法估计是回归系数的最佳线性无偏估计。本文研究误差不满足高斯- 马尔可夫定理要求时,用最小二乘方法对双误差条件下TDOA目标定位模型((7)式)求解的性能。限于篇幅,本文仅分析目标距离估计网络较远的情况。
为了方便对比,在2.1节给出Chan算法的两步加权最小二乘方法的求解步骤;在2.2节给出本文所提基于WTLS,包括推导协方差矩阵的表达式并给出定权方法,建立约束优化模型,基于Lagrange乘数法推导迭代表示式,最后给出求解步骤。
2.1 两步WLS方法
WLS方法忽略了模型(7)式中的节点自定位误差包括乘性误差,仅考虑距离差估计的测量误差,则模型(7)式可表示为
Gaz=h,
(8)
式中:h=ha+Δh=
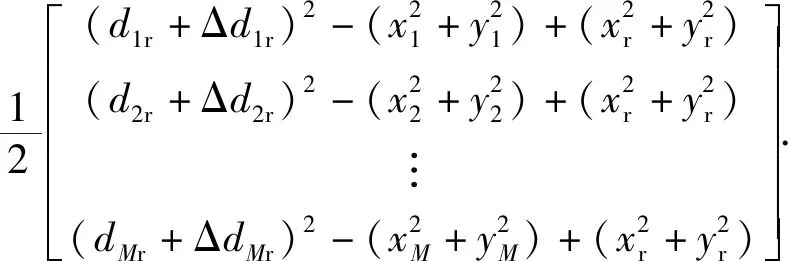
(8)式的求解问题可表示为如下优化问题:
(9)
由于模型(8)式中的误差仅是由距离估计误差引起,则误差可表示为
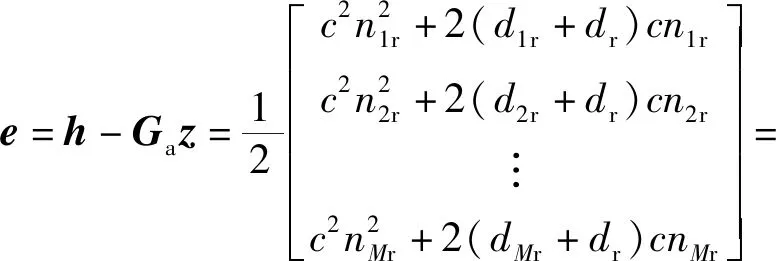
(10)
式中:B=diag(d1r+dr,d2r+dr,…,dMr+dr),且BT=B;n=[n1r,n2r,…,nMr]T服从均值为0、协方差矩阵为Q的高斯分布;符号⊙表示Hadamard乘积。
由于dkr+dr≫cnkr,忽略其高阶项,e≈cBn也服从均值为0的高斯分布,其协方差矩阵可表示为
Σ=Cov(e,e)=E[eeT]≈
c2BE[nnT]BT=c2BQB,
(11)
式中:Cov(e,e)表示求e的协方差矩阵;E[·]表示·的数学期望。
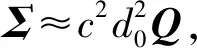
(12)
式中:z取决于Σ(或Q)的矩阵结构,而与其缩放比例无关。考虑到z中dr与[x,y]T的相关性,Chan给出了两步WLS的算法[13]。该算法的具体步骤如下:
步骤1利用WLS对模型(8)式计算,得到初始解
式中:za为z的估计值。由于目标距离较远,可用Q代替Σ,得
步骤2利用步骤1的估计值重新构造一组误差方程组进行第2次估计。重构的方程组为
由此得到优化函数为
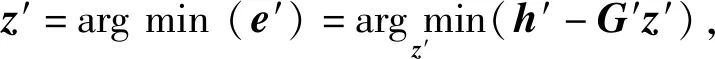
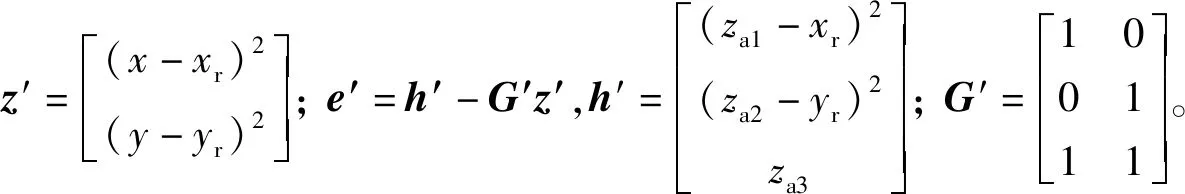
再次使用加权最小二乘法,得
z′≈(G′TB′-1GQ-1GB′-1G′)-1G′TB′-1GQ-1GB′-1h,
其中B′=diag[(za1-xr),(za2-yr),za3]。
步骤3Chan算法得到的最终目标位置估计值为
2.2 WTLS方法
(7)式表示的双误差条件下TDOA目标定位模型是变量(因变量和自变量)包含误差(EIV)模型[17],进一步可表示为
(13)
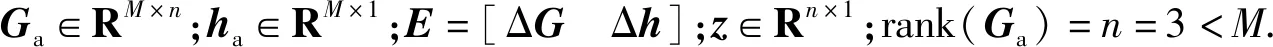
为了方便推导,忽略Δh中的高阶项,得
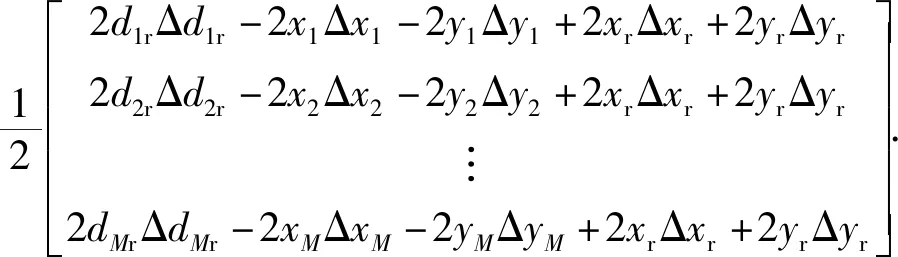
由假设条件及(13)式可知,加性噪声矩阵和乘性噪声矩阵服从如下分布:
(14)
式中:vec(·)表示矩阵按列向量拉直;Σh和ΣG分别为Δh和ΔG的协方差矩阵,
(15)
(16)
G1、G2、G3为ΔG的3个列向量,其对应的协方差矩阵分别为ΣG1、ΣG2、ΣG3,G1、G2、G3之间是相互独立的,因此ΣG中除ΣG1、ΣG2、ΣG3外的元素都为M阶零矩阵0.

由此可推导出
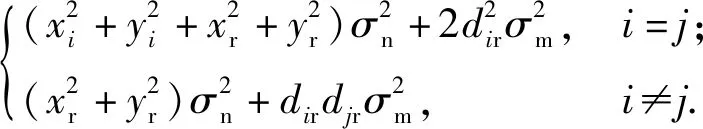
分别为协方差矩阵ΣG的3个分块矩阵。
EIV模型的TDOA目标定位问题可转化为如下条件优化问题:
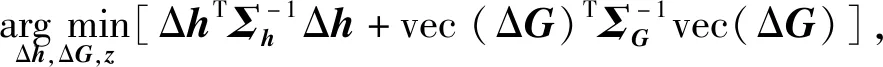
(17)
本文使用Schaffrin[18]等提出的方法进行定权,即要求协方差矩阵ΣG被分解为(18)式的形式:
ΣG=Qx⊗Q0,
(18)
式中:
(17)式所示的优化问题可转化为下列约束优化问题:

(19)
本文按Lagrange乘数法求解,于是构造目标函数如下:
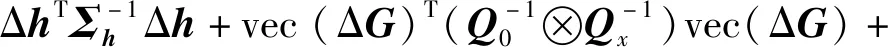
(20)
式中:拉格朗日因子λ∈RM×1.
对(20)式中的Δh、vec(ΔG)、λ和z分别求偏导数,并使其等于0,可以得到
(21)

(22)
(23)
(24)
(21)式、(22)式代入(23)式,得
=[Σh+(TQ0)Qx]-1(ha-Ga).
(25)
(25)式代入(21)式及(22)式,得
Δ=-Σh[Σh+(TQ0)Qx]-1(ha-Ga),
Δ=Qx[Σh+(TQ0)Qx]-1(ha-Ga)TQ0.
(26)
(25)式、(26)式代入(24)式,得
=(ha-Ga)T(Σh+(TQ0)Qx)-1·
Qx(Σh+(TQ0)Qx)-1(ha-Ga),
(27)
(28)
通过推导可知,本文所提基于WTLS的方法充分利用了误差的先验信息得到估计值,但是WTLS问题目前无法得出解析解,只能通过迭代的方法进行数值求解。若得到测量值G=Ga+ΔG,h=ha+Δh,则算法迭代过程如下:
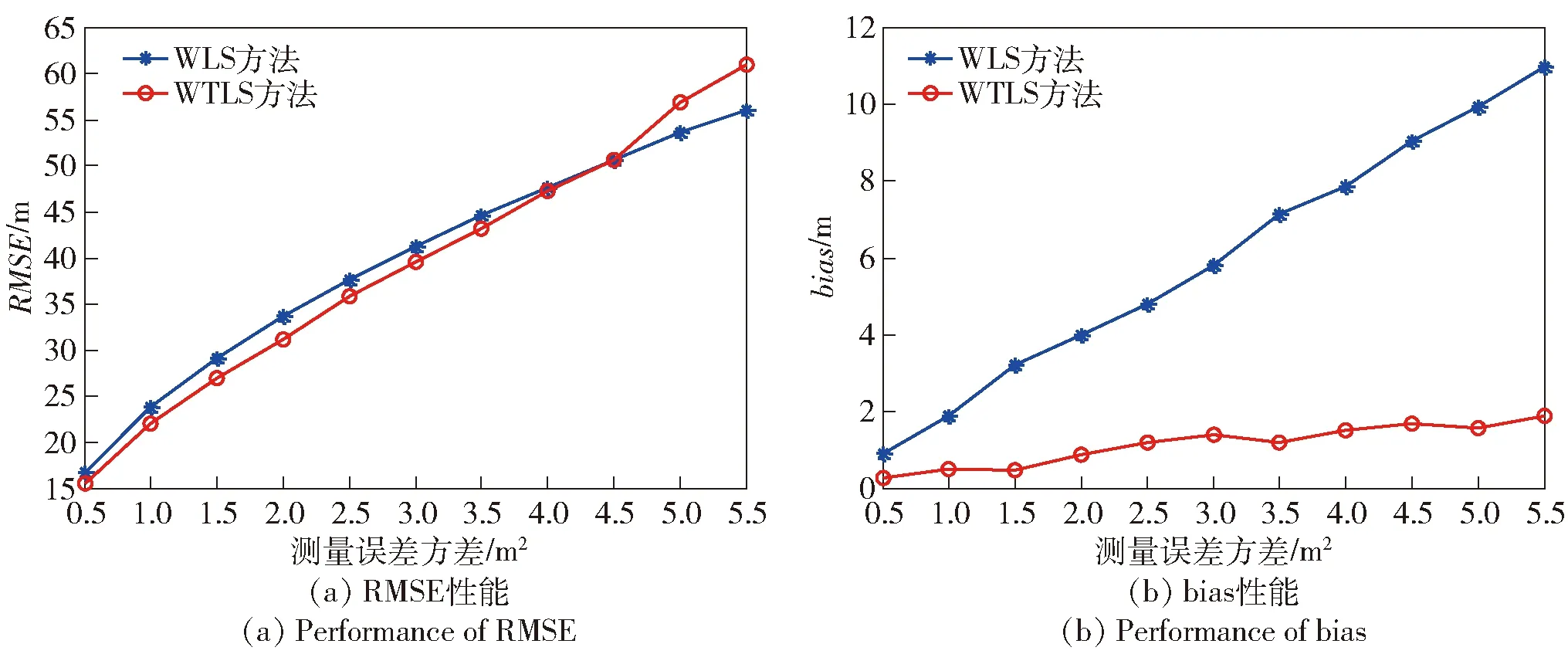
图2 传感器节点无误差时测量误差对估计性能的影响Fig.2 Influence of measured error on estimation performance when sensor node has no error
步骤1未知量的初次迭代值
(1)=(GT(Σh+((0)TQ0(0))Qx)-1G)-1·
GT(Σh+((0)TQ0(0))Qx)-1h.
步骤2给出迭代过程中要求解的两个迭代量(i)和(i),i表示迭代次数,
(i)=(h-G(i))T(Σh+((i)TQ0(i))Qx)-1·
Qx(Σh+((i)TQ0(i))Qx)-1(h-Ga(i)),
(i+1)=(GT(Σh+((i)TQ0(i))Qx)-1G-(i)Q0)-1·
GT(Σh+((i)TQ0(i))Qx)-1h.
步骤3重复步骤2,给出一个阈值ε,当‖z(i+1)-z(i)‖<ε时,计算结束。
步骤4输出结果z(i+1)的前两项,即为u目标真实位置的值。
3 定位方法性能及复杂度仿真和试验
3.1 定位方法性能评价指标
评价定位方法性能的指标通常用均方根误差(RMSE)和偏差(bias),其定义分别为
(29)
(30)
3.2 误差大小对估计性能影响的仿真及分析
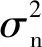
不同误差大小对定位性能影响的仿真结果如下:
1)节点位置无误差时,测量误差对目标定位性能的影响如图2所示。
2)节点位置误差的方差分别为0.01 m2、0.50 m2和3.00 m2时仿真结果如图3所示。
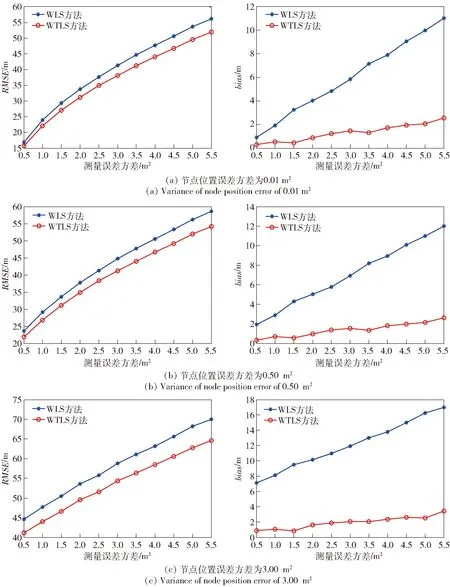
图3 传感器节点位置误差方差一定时测量误差对估计性能的影响(左为RMSE性能,右为bias性能)Fig.3 Influence of measured error on the estimation performance when the position error variance of sensor node is constant (left:performance of RMSE;right:performance of bias)
3)测量误差分别为0.01 m2、0.50 m2和3.00 m2时的仿真结果如图4所示。
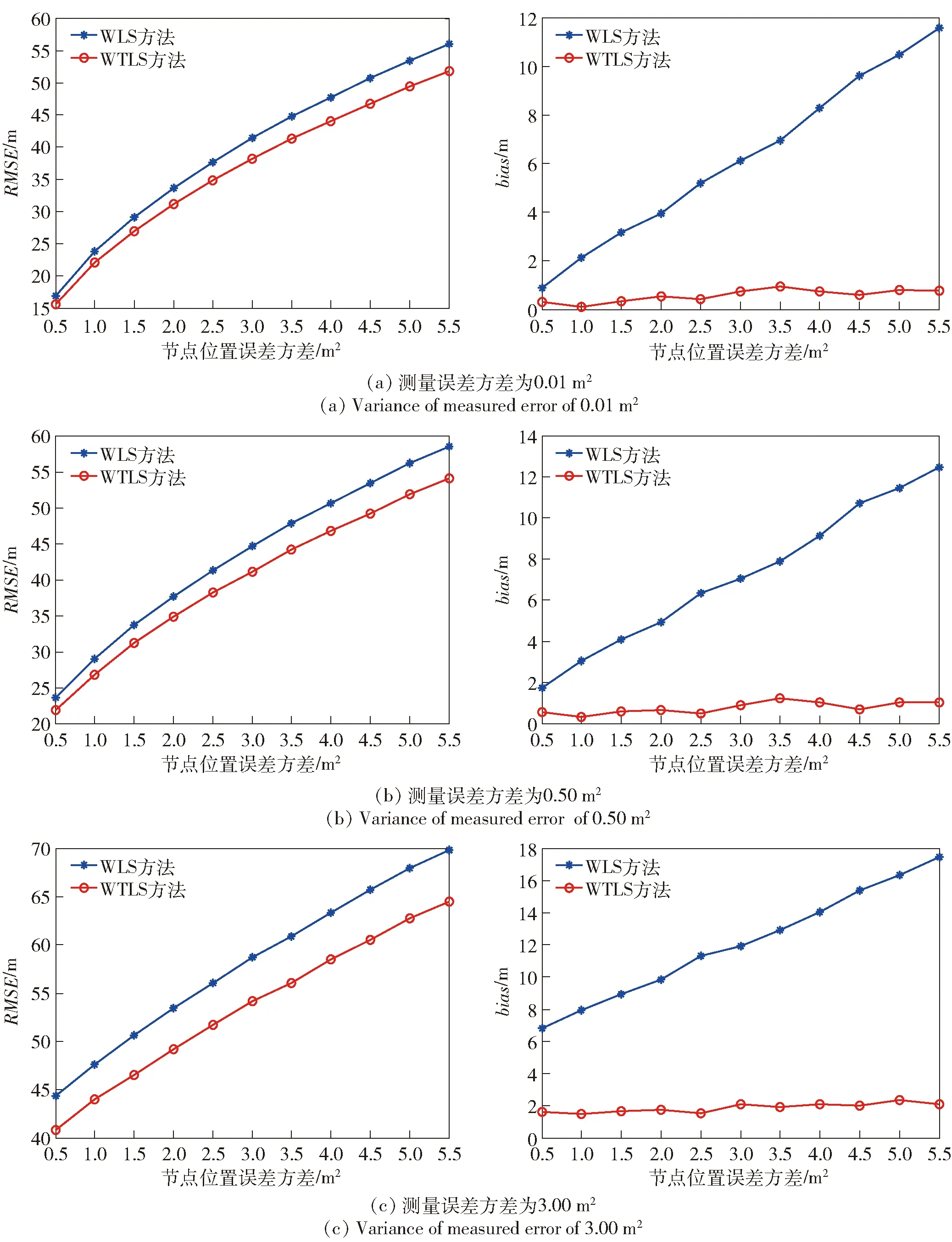
图4 测量误差方差一定时传感器节点位置误差对估计性能的影响(左为RMSE性能,右为bias性能)Fig.4 Influence of position error of sensor node on estimation performance when the measurement error variance is constant (left:performance of RMSE;right:performance of bias)
从图2~图4中可看出:随着误差的增大,两种方法对节点估计的均方根误差也随着增大,WTLS方法的均方根误差略小于WLS方法;WTLS方法的偏差比WLS方法的偏差小很多。究其原因,是因为WTLS方法的模型更准确。
从图2中可看出,当节点位置准确时,WTLS方法和WLS方法的均方误差基本相当,而WTLS方法的偏差比WLS方法小。这是因为WTLS方法的模型考虑了乘性误差,而WLS方法的模型未考虑乘性误差,即使Chan算法两次运用最小二乘法,对估计偏差性能的提高有限。
对比图3和图4可以看出:节点位置误差和测量误差的大小对两种方法的目标估计均方根误差影响基本相同,这是因为在双误差模型(7)式中的乘性矩阵和加性矩阵中均包含有节点位置误差和测量误差;当测量误差一定时,节点位置误差的大小对WTLS方法的偏差影响较小,这是因为WTLS方法的模型更精确。
3.3 节点个数对估计性能影响的仿真及分析
节点位置误差和测量误差的方差均为0.50 m2,节点个数从3~12变化,3.2节中其他仿真条件不变时的仿真结果如图5所示。
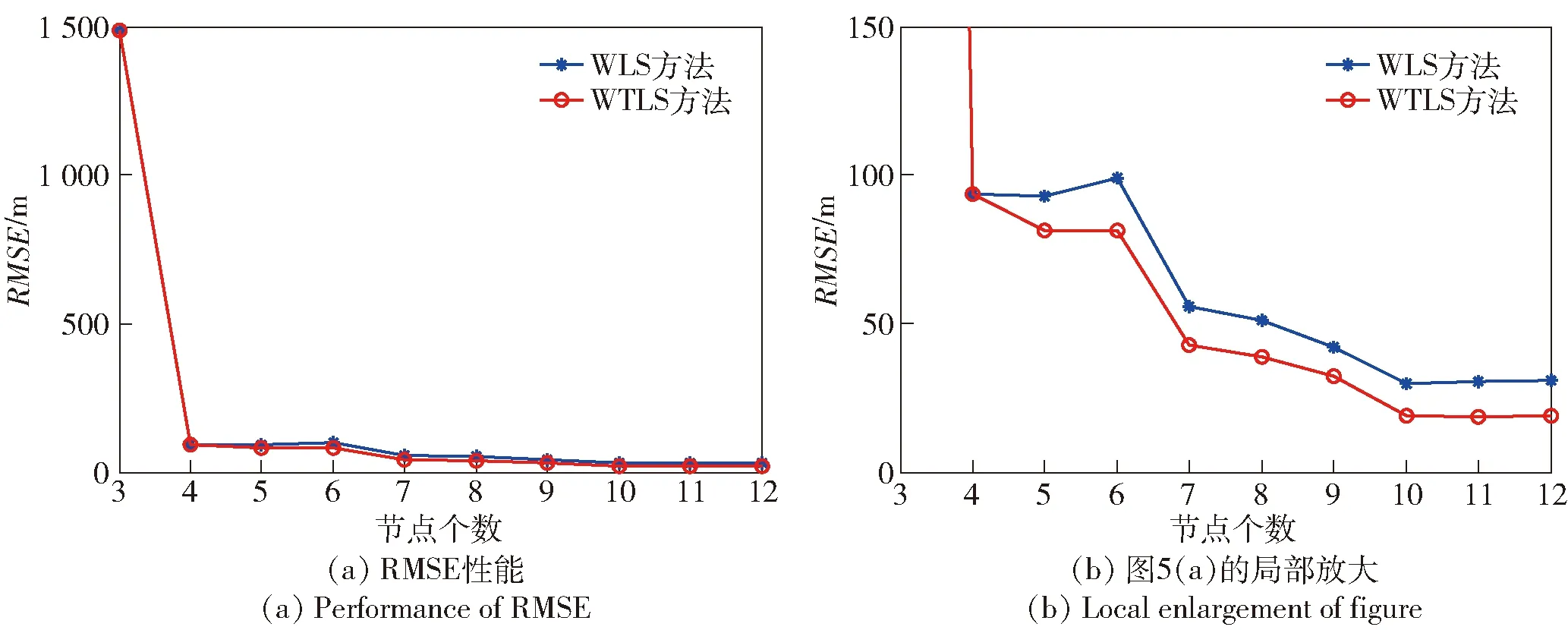
图5 传感器节点个数对估计性能的影响Fig.5 Influence of the number of sensor nodes on the estimation performance
由图5可知,节点个数的多少对两种方法性能的影响基本相当。当节点个数由3增加到4时,两种估计方法的性能均有很大提升,但当节点个数继续增大时,估计性能提升值很小。这是因为虽然节点个数的提升可提高估计性能,但是每个节点都是有误差的,节点的误差又影响了估计的性能。
3.4 定位方法复杂度仿真和分析
对于WLS和WTLS两种定位方法的复杂度,本文采用相对计算时间来衡量,在i5-6500处理器的Win7_64位台式计算机上,用MATLAB2014b软件完成复杂度比较的仿真。

表1 WLS和WTLS的相对计算时间比较Tab.1 Comparison of relative computation times of WLS and WTLS
表1中,对WLS和WTLS中ε取不同值时的相对计算时间进行了比较,将WLS的计算时间作为1.00,WTLS中ε=10、ε=5、ε=1、ε=10-11时的相对计算时间分别为1.33、1.43、1.50、1.98.从表1中的数据可以看出,WTLS的计算时间要多于WLS的计算时间,随着阈值ε减小,WTLS的计算时间在增加,但同时定位性能也在改善。因此,算法定位性能和计算时间要统筹分析,根据需求选择算法对应的ε值。
3.5 定位方法的水池试验和结果分析
为了验证本文所提WTLS法的定位效果,在西北工业大学消声水池进行试验验证。水池试验现场和节点如图6所示,其中:图6(a)是水池试验现场,水池长20 m、宽8 m、深7 m、水深6.8 m;图6(b)是试验用的节点,布放在水深3 m处,共有5个节点,将其中1个节点作为待定位的目标,其他节点作为网络节点。

图6 水池试验现场和节点Fig.6 Experimental site and node
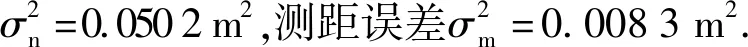
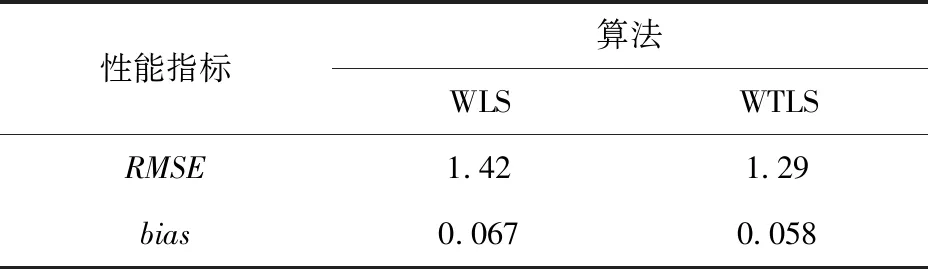
表2 WLS和WTLS试验效果比较Tab.2 Comparison of experimental results of WLS and WTLS m
从表2中可以看出,WLS、WTLS方法的性能都比较好。除算法本身之外,本文设计的试验节点具有偏差补偿的功能。表2中,对比来看,在RMSE、bias方面,本文提出的WTLS定位效果都要比WLS定位效果好。
4 结论
针对水声传感器网络目标定位中传感器节点位置误差大不能忽略的情况,同时考虑测量误差及传感器节点位置误差,本文构造了双误差条件下的TDOA目标定位模型。采用该模型,提出一种基于WTLS的求解算法,推导出协方差矩阵的表达式并给出定权方法。基于Lagrange乘数法,推导出迭代表达式,给出求解步骤。
本文所提方法在模型上同时考虑了两种误差,在求解方法上利用了误差的先验信息,仿真和水池试验结果均表明:双误差条件下WTLS目标定位方法的RMSE和bias均小于WLS方法的RMSE和bias.
