基于多特征量的海杂波参数估计

何耀民，何华锋，徐永壮，王依繁，苏敬

(火箭军工程大学 导弹工程学院，陕西 西安 710025)

0 引言

海杂波是指雷达在海面上形成的散射回波，海杂波受波浪、海风和潮汐等复杂环境的影响。为有效评估不同海况下弹载合成孔径雷达(SAR)成像性能，迫切需要深入分析不同海况下的杂波模型。

关于海杂波模型的研究，主要采用统计分布方法，例如对数正态分布、Weibull分布和K分布等。由于K分布模型能兼顾海杂波的幅度分布特征和脉间相关性能，较其他模型更能准确反映海杂波的统计特性。Marier[1]、Conte等[2]分别利用球不变随机过程(SIRP)法和零记忆非线性(ZMNL)变换法对海杂波进行了仿真。基于上述两种方法，大多学者对其进行了应用或改进：Ritchie等[3]通过杂波数据的累积振幅求解虚警概率，估计海杂波的统计量；Watts[4]和Watts等[5-6]利用多普勒谱测量结果，分析了平均功率谱密度和极值振幅等主要特征，提出基于复合K分布的海杂波模型，并通过大量测试数据进行了模型验证；Weinberg[7-8]利用相互独立的高斯矢量加权乘积构造正交分量，提出计算更简单的KK分布海杂波模型。

针对海杂波的模型参数，目前主要通过经验公式或参数估计求解，常用的经验公式有Ward模型[9]、Ryan模型[10]等。由于海杂波不仅受雷达频率、入射余角、极化方式和分辨单元等固有属性影响，还与风速、风向、海况、雨等自然因素紧密相关，因此针对实际作战海域的某型弹载SAR，基于经验公式的参数推导较难准确贴近真实海况。相比之下，基于实测数据的参数估计法更能反映具体海域的杂波特性。常用的参数估计法包括矩估计法、最大似然估计法和混合估计法等。Blacknell等[11]利用对数估计量法进行改进，可提高模型参数的估计精度；Bocquet[12]利用平均谐波构造闭形式的参数估计模型，避免了求解最大似然估计法中的高维非线性方程，从而简化了计算过程；Balleri等[13]结合最大似然估计和分数矩法进行参数估计，并通过大量数据验证了该混合模型的适用性。此外，也有学者将拟合度分析[14]、神经网络[15]等方法运用于参数估计。

上述文献都是通过各阶矩的计算量或概率密度函数来吻合实测数据，通常能较好地反映出杂波的整体分布趋势，具有一定的参考价值，但未能精确拟合海杂波幅度分布的峰值、幅度宽度等多个特征量。本文建立基于多特征量的参数估计法：首先建立基于SIRP法的海杂波模型，然后针对传统参数估计法对特征点拟合效果差的问题，构造反映海杂波幅度分布的4个特征量，并分析其对尺度参数、形状参数的影响；进而利用实测数据和反向传播(BP)神经网络求解模型参数，建立海杂波幅度分布模型；最后，通过不同海况下后向散射系数确定海杂波的信号功率，为评估不同海况下弹载SAR成像性能提供了杂波模型。

1 基于SIRP法的海杂波模型

K分布模型[16]由散斑分量(受瑞利分布影响)和调制分量(受伽马分布影响)组成，该模型能兼顾海杂波的幅度分布特性和脉间相关性能，是目前使用较广泛的海杂波模型。

1.1 幅度分布特性

海杂波的幅度分布特性可由其概率密度函数[17]表示，如(1)式所示：

(1)

式中：f(x;υ,α)为概率密度函数，x为海杂波的幅度，υ为形状参数，α为尺度参数；Γ(υ)为伽马函数；Kη为η阶贝塞尔函数。通常，υ趋于0时有较长拖尾，趋于∞时逼近瑞利分布。

1.2 时间相关性

海杂波的时间相关性可由其高斯功率谱密度[18]表示，如(2)式所示：

(2)

式中：S(f)为高斯功率谱密度，f为海杂波频率；fD为平均多普勒频移；σf=2σ/λ为杂波频谱均方根，σ为杂波速度的均方根，λ为雷达波长。

由于弹载SAR常采用频率捷变方式抑制海杂波(频率捷变对海杂波谱具有白化作用)，可较大程度削弱其相关性[19]；且不同海况下杂波对成像性能的影响主要体现在信干比、图像斑点、分辨率等功率方面。基于上述两点考虑，本文采用经验公式[9]推导σ、fd，重点考虑形状参数和尺度参数的求解。

1.3 基于SIRP法的海杂波模型

在综合分析海杂波幅度分布特征和时间相关性的基础上，建立基于SIPR法[1]的海杂波模型，如图1所示。图1中：k为海杂波序列数；Y(k)为散斑分量；Z(k)为实白高斯噪声；S(k)为调制分量。

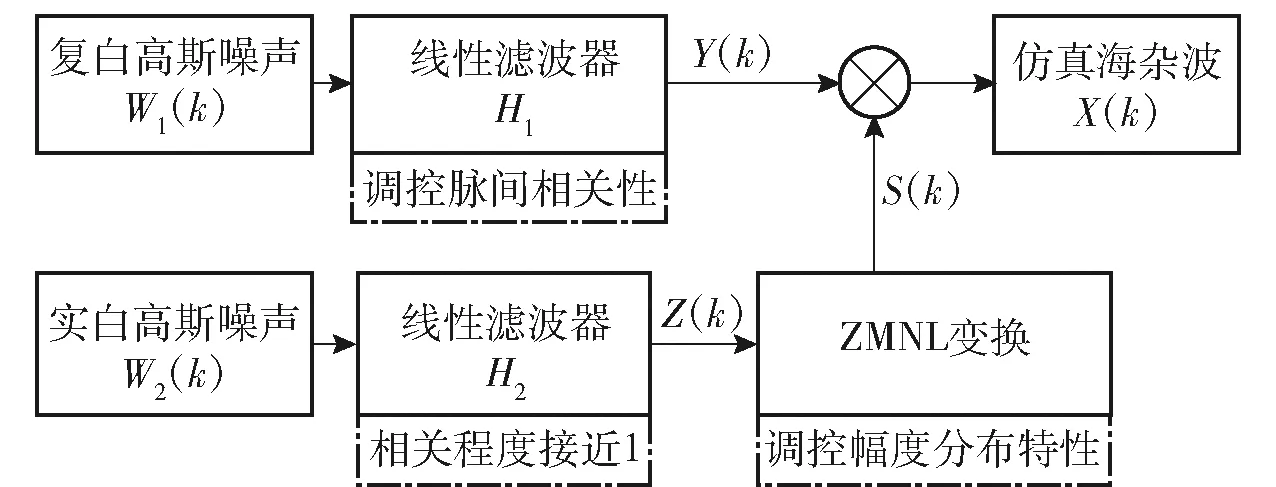
图1 基于SIRP法的海杂波模型Fig.1 Sea clutter model based on SIRP method

如图1所示，SIRP法是模拟雷达的相参机理产生W1、W2两路正交信号：一路由线性滤波器H1处理复白高斯噪声W1(k)，可由高斯功率谱S调控产生散斑分量Y(k)，该分量主要调控海杂波的脉间相关性；另一路由线性滤波器H2调控实白高斯噪声W2(k)生成Z(k)，使其相关性接近1，故海杂波的相关性主要受线性滤波器H1影响；再由ZMNL变换控制杂波的幅度分布特征，可由概率密度函数f调控Z(k)生成调制分量S(k)；最后，由散斑分量Y(k)和调制分量S(k)合成海杂波X(k)。

基于上述仿真建模，海杂波参数主要包括形状参数v、尺度参数α.本文将采用基于多特征量的参数估计法，并结合实测数据进行求解。

2 基于多特征量的参数估计

传统参数估计法包括矩估计法、最大似然估计法和混合估计法等。此类方法通常利用各阶矩的计算量或概率密度函数来吻合实测数据，虽然能较好地反映杂波的整体分布趋势，但对于多个海杂波特征量的拟合效果欠佳。因此，本文通过构造反映海杂波幅度分布的4个特征量，建立基于多特征量的参数估计模型。

2.1 海杂波幅度分布的特征量

在评估不同海况下弹载SAR成像性能时，从幅度分布、信号功率和实测数据波动大等方面考虑，相比于提高海杂波的整体吻合度，把握住其幅度分布的多个特征点更具有实际意义。因此，本文借鉴雷达回波信号的幅度分布图[20]，构造出反映海杂波幅度分布的4个特征量，如图2所示。

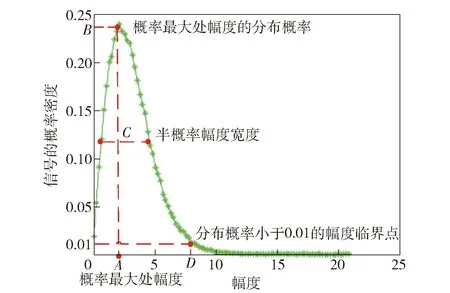
图2 幅度分布函数的4个特征量Fig.2 Four characteristic quantities of amplitude distribution function

观察图2可知，4个特征量分别为：1)分布概率最大处所对应的幅度A；2)概率最大处幅度的分布概率B；3)半概率幅度宽度C；4)分布概率小于0.01的幅度临界点D.通过构造上述4个特征量，即可确定海杂波的幅度分布函数。

2.2 模型参数分析

2.2.1 尺度参数

尺度参数α反映了海杂波回波信号的功率特性，即参数越大、幅度越高[21-22]。根据第1节中的海杂波模型，令σ=1、fD=0 Hz、υ=2，α为单一变量进行仿真，分析其对4个幅度特征量的影响，各特征量的变化趋势如图3所示。

观察图3(a)、图3(c)、图3(d)可知，当尺度参数α在[0，4]范围内增大时，概率最大处的幅度A、半概率幅度宽度C和幅度临界点D均为单调递增；观察图3(b)可知，杂波幅度最大处所对应概率B为单调递减。结合尺度参数与幅度间联系[21-22]可知，图3(a)、图3(c)、图3(d)的仿真结果与α的物理意义相吻合。另外，由图3(b)可见，尺度参数越大时，杂波幅度分布趋势越平缓。为证明上述结论在其他参数情况下仍然适用，令σ=2、fD=100 Hz、υ=3，所得仿真结果与图3十分相似，从而表明上述关于尺度参数分析的正确性。

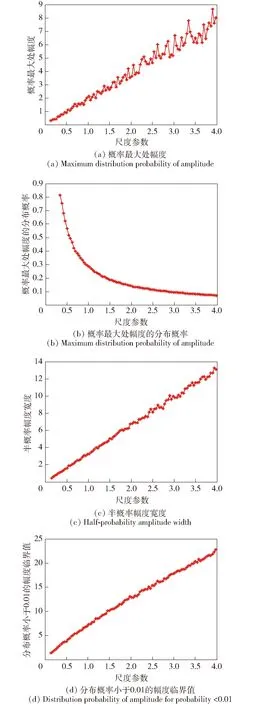
图3 尺度参数对海杂波幅度分布的影响Fig.3 Influence of scale parameter on amplitude distribution of sea clutter

2.2.2 形状参数

目前常用的形状参数ν推导公式[17]如下：

(3)

式中：φ为入射余角；SA为有效受照区域；δ为风向参数，在顺风时δ为-0.34、逆风时δ为0.34；K1为极化方式参数，在水平极化时K1为2.09、垂直极化时K1为1.39.

由(3)式可知：形状参数通常与入射余角、照射区域、风向、极化方式等因素有关，与信号幅度的联系不太紧密(已通过BP神经网络仿真验证：若单独通过幅度分布预测形状参数，则其决定系数<0.8)；另外，对于K分布海杂波，通常认为杂波平均功率为4υα2，即形状参数ν与尺度参数α相关联[17]。基于以上分析，为增强形状参数和4个幅度分布特征间的联系，将尺度参数作为限定因素加入幅度分布特性中。

2.3 BP神经网络求解参数

通过2.2节分析可知：形状参数ν、尺度参数α与幅度分布函数的4个特征量是紧密相关的，因此可通过求解二者间的定量关系确定模型参数。但由于ν、α与4个幅度分布特征间为非线性、高阶次对应关系，直接求解存在较大难度，故选用BP神经网络来挖掘数据间的定量关系。

BP神经网络[23-25]由一个输入层、若干个隐含层和一个输出层组成，各层均有一个或多个神经元节点。该模型利用误差逆传播算法，通过调整各层连接权值，从而使目标输出和实际输出满足在一定误差范围内。本文参考遗传算法[26]建立BP神经网络模型，将贝叶斯正则化方法作为模型训练函数，如(4)式所示：

F=φEw+βEd，

(4)

式中：F为模型训练函数；Ew为整个训练网络的权值平方和；Ed为各层网络误差值；φ和β为正则化系数。利用BP神经网络求解模型参数的算法流程如图4所示，其中A0、B0、C0、D0为实况海杂波数据的4个特征量。

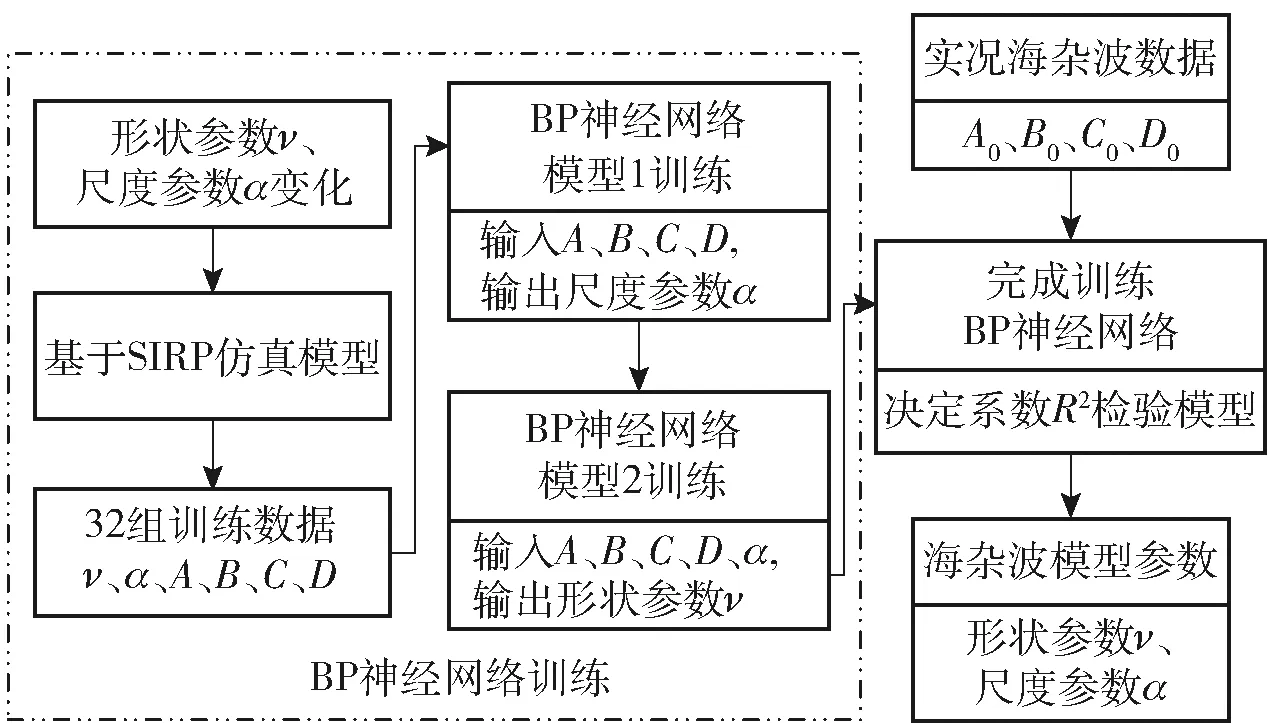
图4 BP神经网络的算法流程图Fig.4 Algorithm flow chart of BP neural network

在建立上述BP神经网络模型的基础上，可利用实测数据求解尺度参数和形状参数，从而确定海杂波的幅度分布模型。

2.4 不同海况的信号功率

描述海表面时，通常采用数字等级表示海表面状态的恶劣程度。一般认为海表面状态和风速的关系如下：只有当风在足够大风浪区且持续足够长的时间时，才能激起一个充分发展的海表面[20]，此时浪高和风速的关系如表1所示。

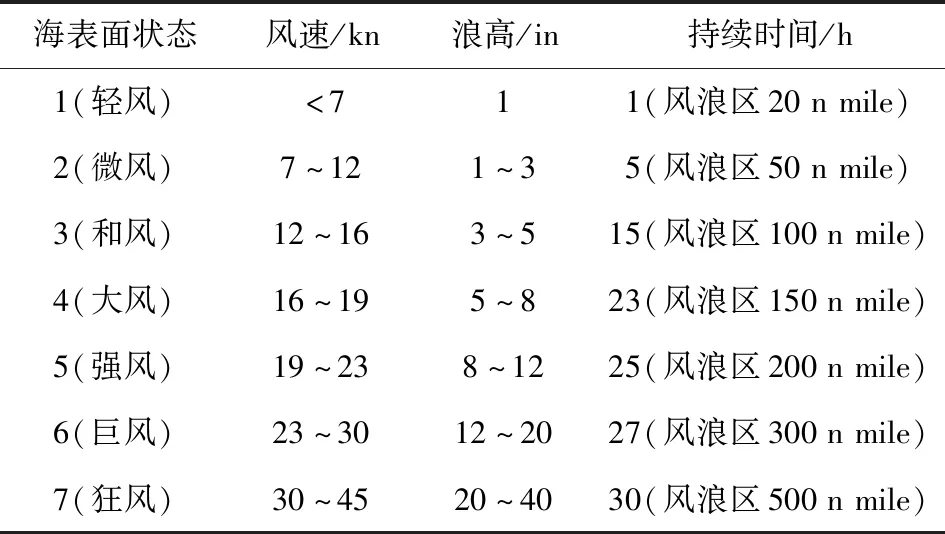
表1 海表面描述Tab.1 Sea surface description

Skolnik在雷达手册[20]中指出：海杂波信号强度随入射余角增大而增大，随风速(或海表面状态)增强而增强。另外，工程应用中通过利用后向散射系数计算信干比。因此，本文采用后向散射系数分析不同海况下杂波的信号功率。

SAR图像的信杂比计算公式如下：

(5)

式中：Ps为雷达信号功率；Pc为杂波功率；σr为打击目标的雷达散射截面；γ为入射余角；σ0为海杂波的后向散射系数；ρr为SAR距离向分辨率；ρa为SAR方位向分辨率。因此，在获取不同海况下后向散射系数的基础上，通过(5)式求解信干比，可确定不同海况下杂波的信号功率，进而可为有效评估不同海况下弹载SAR成像性能提供海杂波模型。

3 模型仿真

利用基于多特征量的参数估计法仿真海杂波模型。首先，分析中国人民解放军海军航空大学在中等入射余角、2级海况下测量的Ku波段数据[27]，按照图4中的BP神经网络求解该海况下杂波模型；然后，利用周平等通过机载海面散射试验测量的Ku波段数据[28]，获得在不同海况下的Ku波段后向散射系数；最后，结合2级海况杂波模型和不同海况下的杂波功率，实现不同海况下的杂波仿真。

3.1 海杂波的幅度分布模型

3.1.1 实测数据

本文中的2级海况杂波数据[27]来自高分辨率Ku波段雷达，信号脉宽为10 μs，距离向分辨率为1.875 m，入射余角44°，其幅度分布曲线如图5所示；根据第2节中对幅度分布函数的分析求解4个特征量，如表2所示。

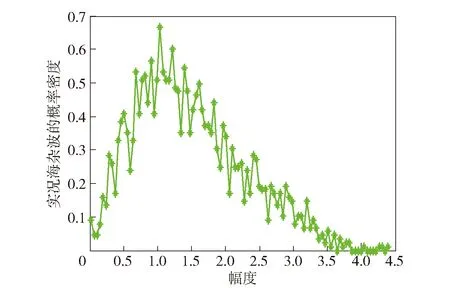
图5 实况海杂波的幅度分布曲线Fig.5 Amplitude distribution curve of real sea clutter

表2 幅度分布函数的4个特征参数Tab.2 Four characteristic quantities of amplitude distribution function

注：概率最大处的概率取相邻3点均值。

3.1.2 神经网络训练

利用第1节的海杂波模型，通过改变形状参数、尺度参数，仿真得出32组不同参数下的海杂波；求解各组海杂波幅度分布的特征量(令概率最大处幅度、概率最大处幅度的分布概率、半概率幅度宽度、概率小于0.01的幅度临界点分别为A、B、C、D)，如表3所示。

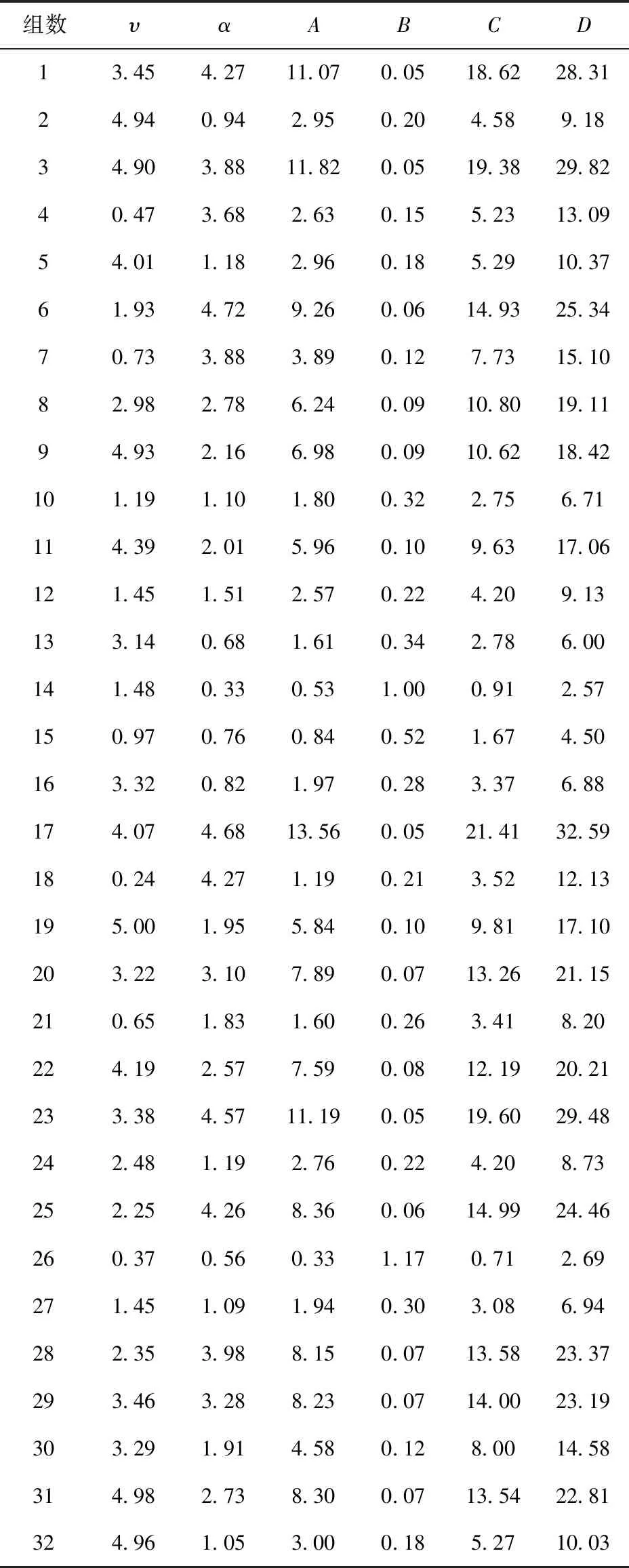
表3 各组海杂波幅度分布函数的特征参数Tab.3 Characteristic parameters of amplitude distribution of sea clutter in each group

3.1.3 求解海杂波模型参数

1)模型1训练。将表3中前28个数据作为训练样本、后4个数据作为测试样本，A、B、C、D为输入、尺度参数α为输出；确定输入、输出层的神经元个数分别为4和1；隐含层数为1、神经元数量为7，学习效率为0.01、训练次数为1 000、误差上限为0.000 1.可得到连接权值W1、阈值S1，完成模型1的训练。

2)模型2训练。参考模型1，将输入扩增为A、B、C、D+α，输出为形状参数υ；输入层的神经元个数改为5，其余参数不变。可得到连接权值W2、阈值S2，即完成模型2的训练。

利用训练好的BP神经网络，分别将归一化训练、测试样本作为输入，利用Bootstrap[29]将数据扩充100倍后，求其预测值；将预测值与实际值进行对比，并用决定系数R2[30]检验模型好坏，决定系数R2计算公式如下：

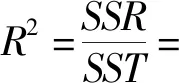
(6)

式中：SSR为回归平方和；SST为总平方和；N为测试样本个数；SA为模型预测值；SB为样本原始值。当决定系数R越高时，模型评估的变化趋势越接近真实值。利用训练好的BP神经网络对尺度参数、形状参数进行预测，其决定系数分别为0.992和0.994，具体如图6、图7所示。

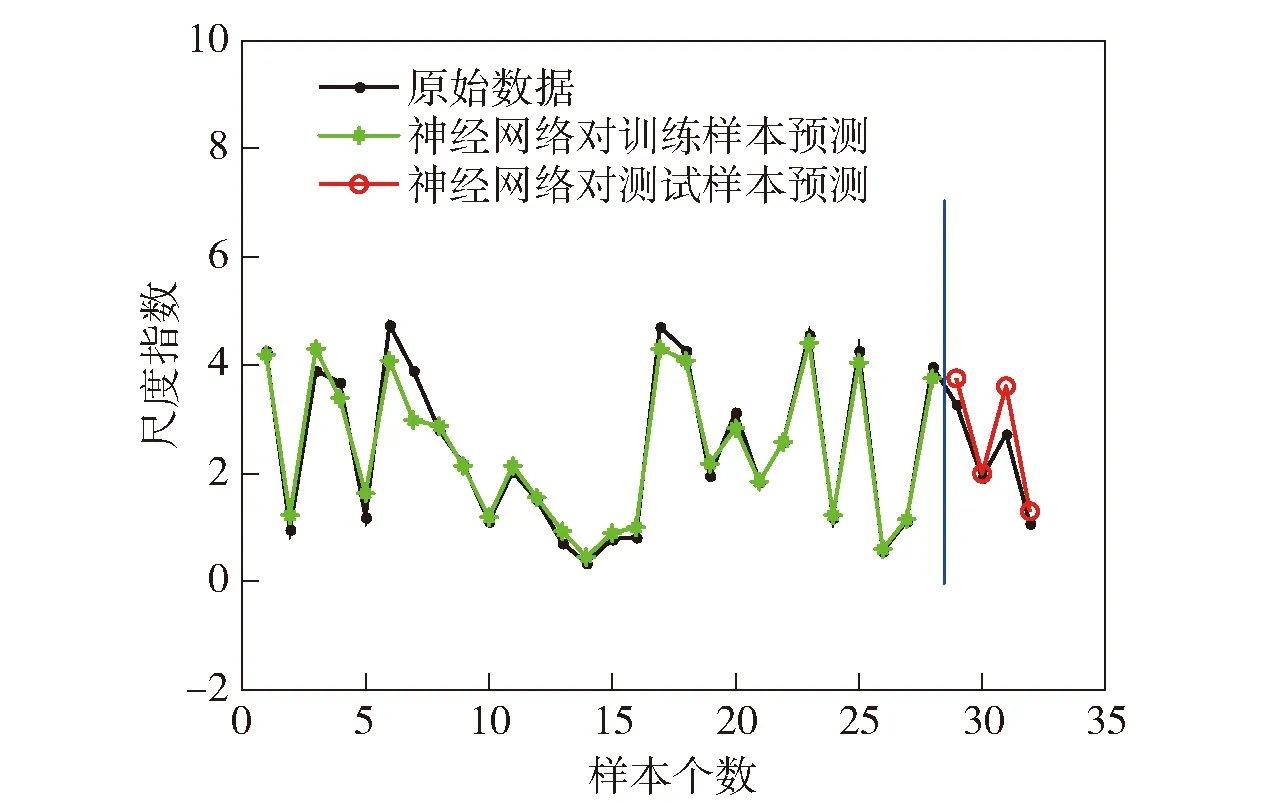
图6 神经网络对尺度参数的预测Fig.6 Prediction of scale parameter by BP neural network

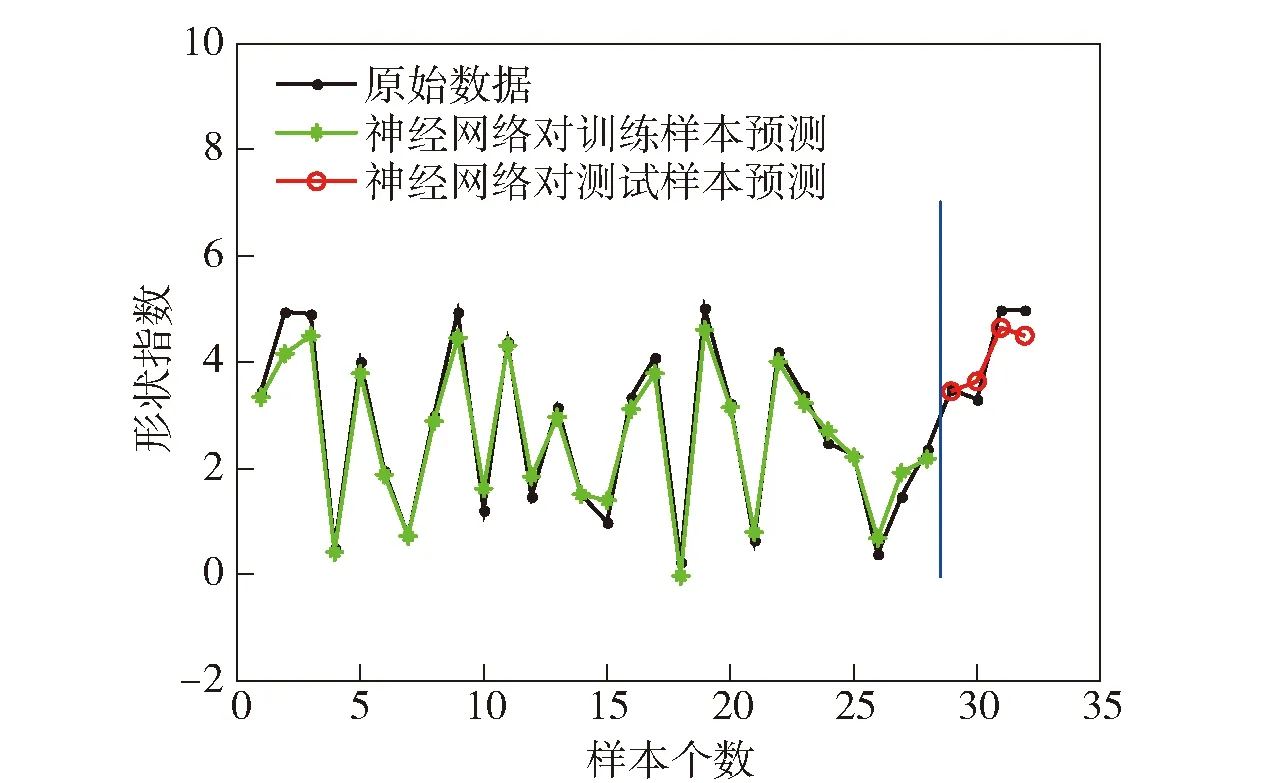
图7 神经网络对形状参数的预测Fig.7 Prediction of shape parameter by BP neural network

最后，利用完成训练的BP神经网络，将表2中的A0、B0、C0、D04个特征量作为模型输入，求解海杂波的模型参数ν和α，如表4所示。

另外，若单独利用4个特征参数求解形状参数ν，则其决定系数仅为0.784，从而验证了2.2节中关于形状参数分析的合理性。

3.2 不同海况的信号功率

3.2.1 后向散射系数

我国目标与环境电磁散射辐射国防科技重点实验室在我国舟山海域开展了机载海面散射测量试验[28]，其雷达为Ku波段、飞行时速为200～250 km/h、入射余角为20°～90°.该试验在顺风、逆风条件下获得了2级、3级、4级海况的后向散射系数，如图8所示。

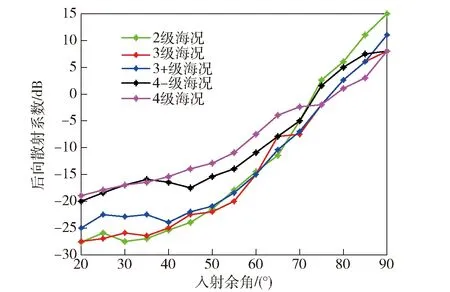
图8 不同海况下杂波的后向散射系数Fig.8 Back-scattering coefficients under differentsea conditions

根据图8中的实测数据，当入射余角为45°时，不同海况(2级、3级、3+级、4-级、4级)的后向散射系数分别为-24.0 dB、-22.5 dB、-22.0 dB、-17.5 dB、-14.0 dB.

3.2.2 不同海况下的信干比

当弹载SAR打击目标时，令σr为25 dBm2、ρr为5 m、ρa为15 m，根据(5)式计算不同海况下信干比，如表5所示。

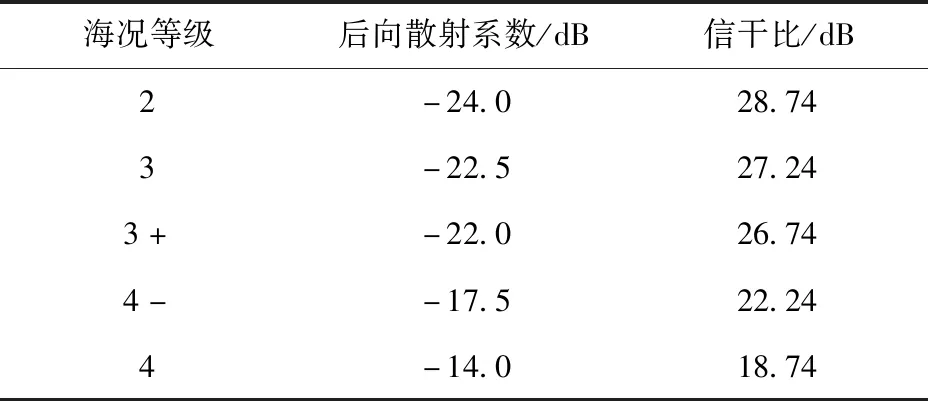
表5 不同海况下信干比Tab.5 Signal-to-interference ratios under different sea conditions

利用上述海杂波幅度分布和不同海况下杂波功率，即可实现不同海况下的杂波仿真，从而为评估不同海况下弹载SAR成像性能提供模型基础。

3.3 方法对比

针对3.1节中海杂波幅度分布模型，分别利用经验公式[9]和混合估计法[13]求解其形状参数、尺度参数，而其杂波速度均方根、多普勒频移则由经验公式[9]获取(σ=1，fD=24 Hz)。比较3种方法和真实海杂波的幅度分布特征，如图9所示。

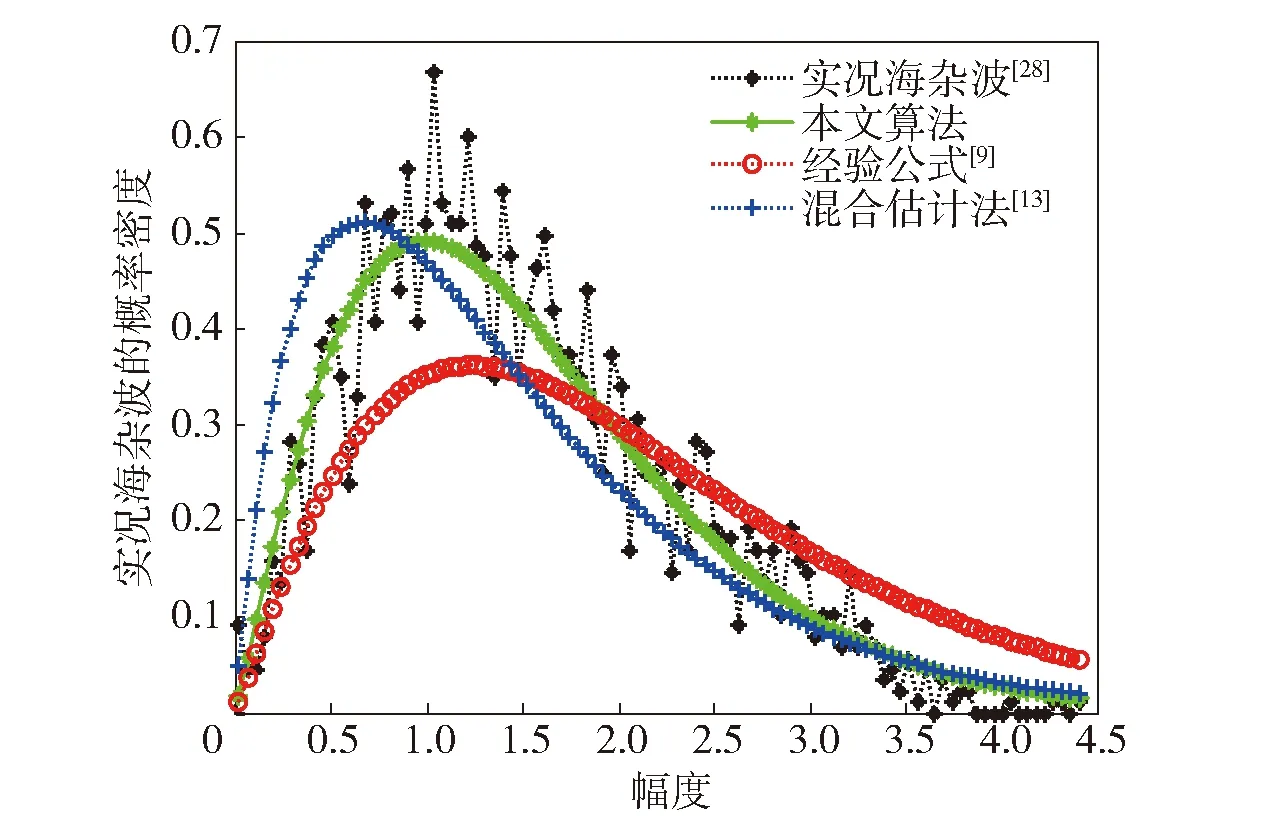
图9 不同方法下海杂波幅度分布特性曲线Fig.9 Amplitude distributions of sea clutter estimated by different methods

从定性角度分析：如图9所示，本文算法(绿色曲线)和混合估计法(蓝色曲线)的幅度分布与实测数据(黑色虚线)基本相符，但混合估计法的概率最大处所对应幅度A偏差更大，且半概率幅度宽度C偏小；另外，相比本文算法和混合估计法，基于经验公式(红色曲线)的估计结果最不理想。

从定量角度分析：用平均相对误差E[27]进行对比(E<0.5为有效拟合)，计算公式如下：

(7)

式中：X为实测数据；Q为估计值；n为数据个数。另外，按照2.1节计算各方法下仿真海杂波幅度分布的4个特征量，如表6所示。

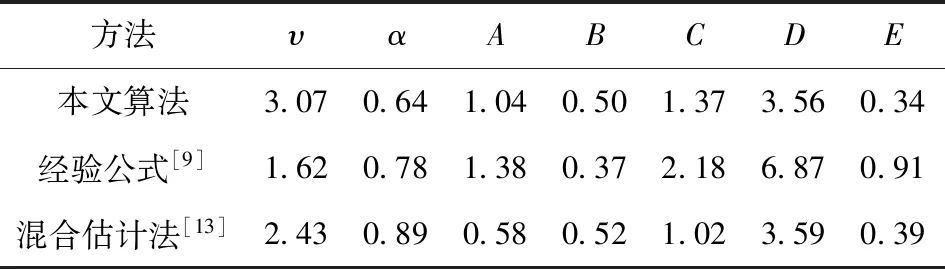
表6 3种参数估计方法对比Tab.6 Comparison of estimated results of three methods

观察表6可知，本文算法和混合估计法在平均相对误差E、概率最大处幅度所对应概率B、概率小于0.01的幅度临界点D都较为近似；但对比表4中实测数据的概率最大处幅度A和半概率幅度宽度C发现，本文算法在A和C的拟合更优于混合估计法，从而表明了本文算法的性能更佳。

4 结论

本文分析了海杂波模型中的形状参数、尺度参数对其幅度分布特性的影响，提出了基于多特征量的参数估计法。结合数学仿真和经验公式的手段分析可知：模型的尺度参数ν、形状参数α与幅度分布函数的4个特征量是紧密相关的；利用实测数据和BP神经网络先后求解尺度参数和形状参数，建立了海杂波的幅度分布模型；在分析不同海况下后向散射特性基础上，利用信干比实现不同海况下的杂波仿真，为有效评估不同海况下弹载SAR成像性能提供了模型依据。下一步将重点研究如何科学建立不同海况下成像性能的评估体系。