基于局部异常因子算法的三维声纳单帧重建研究
2020-04-16曾腾张春华王朋
曾腾,张春华,王朋
(1.中国科学院 声学研究所,北京 100190;2.中国科学院 先进水下信息技术重点实验室,北京 100190;3.中国科学院大学,北京 100049)
0 引言
三维声纳能够获得三维空间信息,实现高分辨率的实时水声探测,在海洋资源开发、海洋地形测绘和水体障碍物探测中有着广泛应用,使得三维声学图像处理的研究变得尤为重要。另外,由于海洋环境的复杂性,声纳系统的性能受背景噪声的限制[1],除环境噪声外,声速的非线性变化以及水池池壁的反射等因素[2],都会使三维成像声纳获取的点云数据存在噪点,直接影响后期三维重建的准确性和效率。因此,在点云重建之前需要进行点云去噪,最大程度地保留目标的轮廓信息,去除图像中的干扰信息。
光斑噪声通常使用平滑有限冲激响应(FIR)滤波器处理,通过对邻域像素点的加权线性组合修复当前像素点,虽然它有较好的去噪平滑效果,但是会导致图像模糊,影响目标识别[3-4]。文献[5]中采用马尔可夫随机场(MRF)模型,利用统计方法建模和反演技术进行去噪,但这种方式实现复杂。阈值法具有实现简单、计算量小、性能较稳定、应用最广泛的特点,能够通过设定阈值区分目标回波与杂波,就噪声降低和质量改进而言,在计算复杂性和性能之间有很好的折衷[6-7]。文献[8]在快速目标检测与追踪背景下,采用双阈值方法实现简单有效的去噪,但是这种方式很难定义2个阈值的选择标准。文献[9]将阈值固定在最大像素值的22%,直接作用于波束信号,但阈值选择过于单一,在去除大部分目标以外的噪点外,还会存在对目标轮廓造成干扰的异常点。
异常点(离群点)的定义最早由Hawkins[10]提出,异常点和数据集中的其他数据产生于不同机制,在数据特性上有很大差异。因此复杂背景和强杂波干扰下,背景和干扰带来的非目标点被视为异常点,可通过目标点和干扰点的差异来进行区分[11-13]。目前异常点检测主要用于数据挖掘领域,主要分为基于统计的方法、基于深度的方法、基于聚类的方法、基于密度的方法和基于距离的方法[14-15]。当数据分布密度相差较大时,基于密度的异常点检测方法能得到更理想的结果[16-20]。局部异常因子(LOF)是一种基于密度的异常点检测方法,其主要思想是基于每个点的密度及其邻域点的密度决定该点是否为异常点。该方法简单直观,不需要对数据分布有过多的要求。
为了获得易识别的目标重建结果,本文首先采用48×48个声学换能器的平面接收阵(512个通道),发射单脉冲声波信号进行128×128个波束形成,对获取到的目标单帧数据依次进行三维波束成像、最大值滤波和坐标系转换,进而得到原始点云,提出基于LOF算法的去噪方法对点云进行平滑,并利用一种改进的三角网生长方法进行单帧重建得到目标重建结果。
1 三维声纳点云模型
1.1 三维波束形成成像技术
假设接收平面阵的阵元数为M×N,阵元各向同性。方位角α与俯仰角β的定义示意图[21]如图1所示。

图1 方位角及俯仰角定义示意图Fig.1 Definition of azimuth and pitch angles
以远场波束形成为背景,其波束形成表达式为
(1)
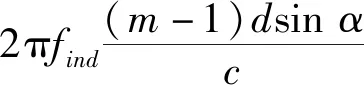
利用FFT实现三维成像声纳的波束形成,在远场对接收信号的频域信号进行空域二维FFT的结果为

(2)
式中:fα为方位角方向上的波数;fβ为俯仰角方向上的波数。
根据上述过程,接收面阵中每个单元接收到不同距离、不同方向上的回波叠加形成混合信号,对48×48个混合信号进行128×128个波束形成,从而得到一系列距离切片,如图2所示,每个切片是128×128个点的反射强度信息集合。图2中:I为数据点强度;i表示数据点在x轴方向上的波束位置;j表示数据点在y轴方向上的波束位置;根据距离采样率,L表示数据点所在的层数,即数据点到接收阵的距离;O(x0、y0、z0)为视角原点。
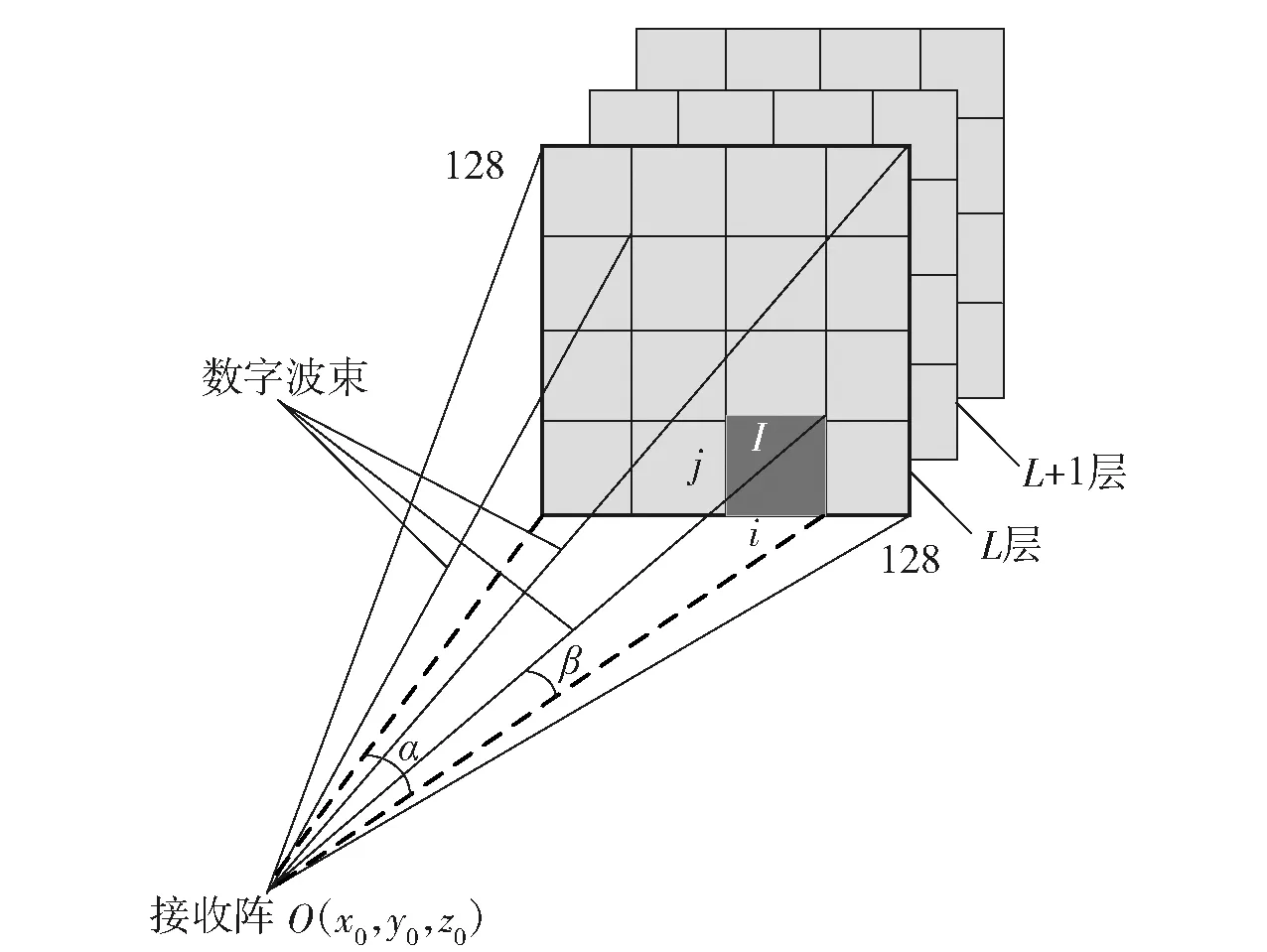
图2 接收阵128×128个波束示意图Fig.2 128×128 beams of receiving array
1.2 三维点云的获取
对接收面阵接收到的声学数据进行解析,声学数据点格式可以表示为(i,j,L,I)。每帧信号得到包含128×128×2 048的体数据,其中距离切片数由声纳成像距离和距离分辨率决定。
由于原始数据的数据量过于庞大、干扰较多,不易获取目标的真实轮廓,对后期的目标分割重建操作有着很大的影响。为了改善这种情况,对体数据进行最大值滤波,即在每一个波束方向的不同距离切片中找到强度最大的数据点位置和对应强度,从而得到128×128大小的目标位置和强度信息矩阵。然后进行坐标转换,将数据点位置映射到三维坐标系下,数据点强度信息作为色彩信息,生成预期的点云数据。
李栋,山西太谷县人,1969年出生,中国诗歌学会会员,山西省作协会员。1992年发起创办太阳谷文学会。2010年起触网写诗,组诗偶见于《人民文学》《诗刊》《星星》等处。
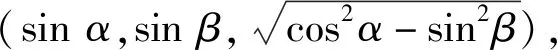
(3)
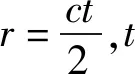
2 算法描述
2.1 基于LOF去噪算法
为了解决阈值方法仍存在异常点的情况,本文针对三维成像声纳获取的数据密度不均匀且维度较高的特性,在阈值去噪基础上,采用一种基于密度的异常点检测方法——LOF检测算法。为了验证该方法的效性,将声纳数据阈值去噪方法和该方法进行性能对比。
LOF算法的主要思想是通过对每个点p及其邻域点的密度判断该点是否为异常点,如果点p的密度越低,则点p是异常点的可能性越大。假设在经过阈值处理后的点云中取任意一点p,其第k距离dk(p)定义为
dk(p)=d(p,o),
(4)
式中:d(p,o)为点p与点o之间的距离。(4)式满足:
1)在输入点云中至少有不包括p在内的k个点o′∈C(x≠p),满足d(p,o′)≤d(p,o);其中x为点集中的点,C(x≠P)为不包括点P的集合,o′为该集合中的某一点。
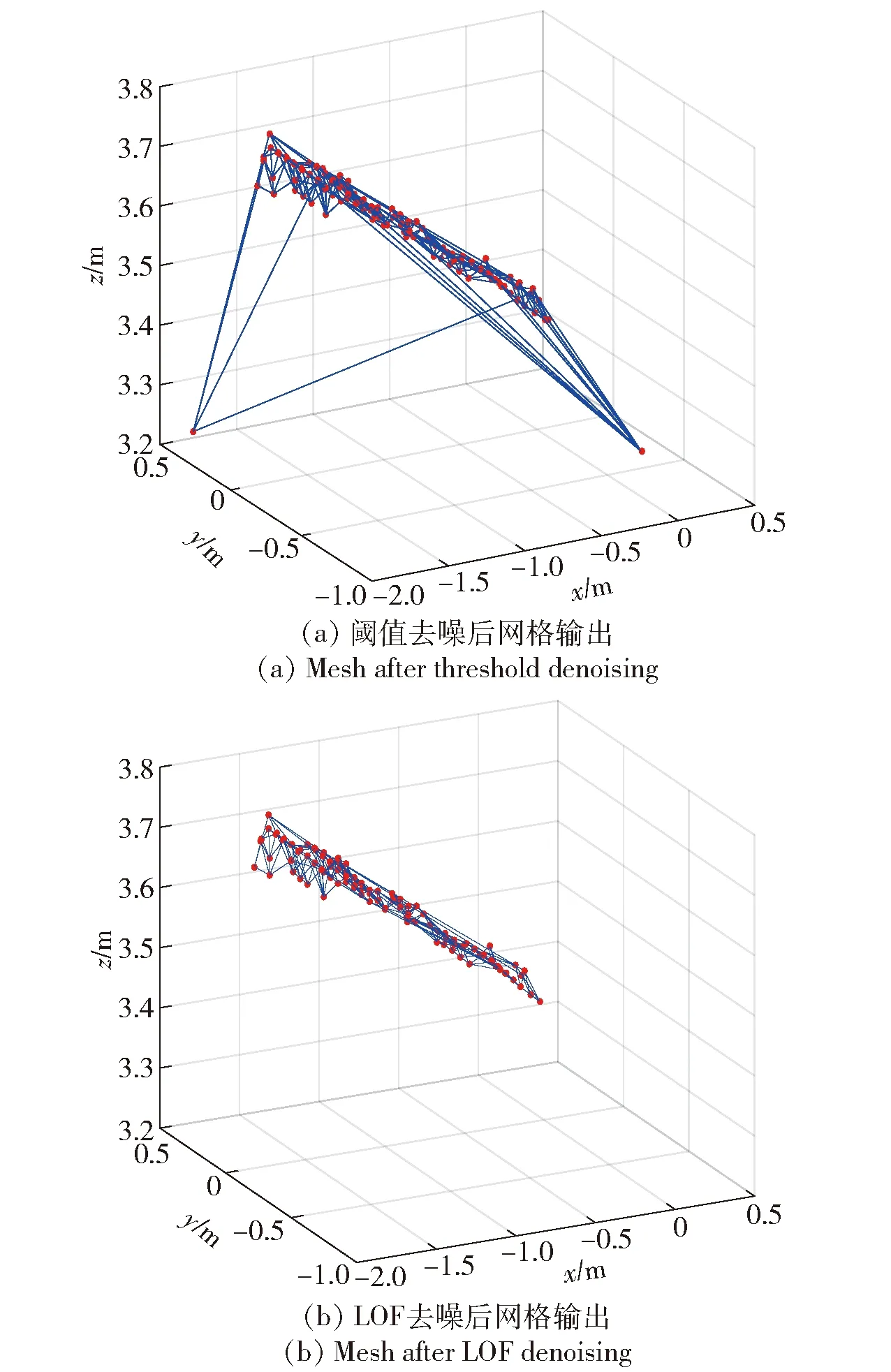
2)在集合中最多有不包括p在内的k-1个点o′∈C(x≠p),满足d(p,o′) Nk(p)={q∈D{p}|d(p,q)≤dk(p)}, (5) 式中:Nk(p)为点p的第k距离邻域;q为点p的邻域点;D{p}表示除点p之外的点云集合。 点p到点o的第k可达距离为 dr(p,o)=max {dk(o),d(p,o)}. (6) (6)式意味着离点o最近的k个点,o到它们的可达距离相等且等于dk(o)。图3所示为k=4的可达距离dr(p1,o)和dr(p2,o)的示意图。 图3 k=4的可达距离示意图Fig.3 Schematic diagram of reach distance for k=4 根据上述定义,点p的局部可达密度表示为 (7) 通过点p的局部可达距离以及点o(点p的邻域点)的局部可达距离作比,构造如下所示的比较因子,即局部离群因子,进而检测异常点: (8) 该比值越接近1,表明点p的密度和其邻域点密度相差不多,p可能与邻域同属一簇;该比值越小于1,表明p的密度高于其邻域点密度,p为密集点;该比值越大于1,表明p的密度小于其邻域点密度,p越可能是异常点。因此,观察LOF值选取合适的值,保留取值范围之内的点,即为异常点去除之后的目标点云。 1979年Brassel和Reif提出了三角网生长算法的主要思想,即首先找出点集中相距最短的两点并连接成一条Delaunay边,然后按Delaunay边三角网的判别法则找出包含此边的Delaunay三角形另一端点,依次处理新生成的边,直至最终完成[22]。三角网生长法的改进实现多表现在搜寻“第三点”的策略上。为了简化搜寻过程、降低算法复杂度,本文利用Delaunay三角网的空圆特性进行构网,即Delaunay三角网中任一三角形的外接圆范围内不会有其他点存在。 图4所示为点p1、p2和第3点p3组成的外接圆。从图4中可以看出,位于外接圆内部的p3对应的三角形内角角度大于外接圆上p3对应的三角形内角角度α2.通过观察不同点对应的三角形内角角度α1、α2和α3,若要实现外接圆内无其他点,则第3点对应的角度最大。 图4 外接圆与第三点关系示意图Fig.4 Relationship between circumcircle and the third point 另外,为了降低扩展三角网搜寻第3点的计算量,在以已有三角形的边为基准扩展时,只搜寻边一侧的点集,将此作为第3点备选点,即第3点与该边相对的点关于该边异侧。由图4可以看出,△p1pp2为已有三角形,以边为基准扩展,新生成的第3点p3与点p关于边对称。首先需要对第三边进行直线方程求解,假设p1坐标为(x1,y1,z1)、p2坐标为(x2,y2,z2),根据直线Ax+By+C=0的一般式方程,代入两点坐标求出系数: (9) 之后基于直线方程寻找满足条件的第3点,假设点p坐标为(x,y,z),第3点p3坐标为(x3,y3,z3),第3点和点p关于已求得的直线满足异侧准则,即: (Ax3+By3+C)(Ax+By+C)<0. (10) 为了检测算法的实用性,对铁管目标进行水池实验。实验场景环境参数如下:声纳系统入水深度2.0 m,目标与声纳系统的距离为3.4 m,声纳系统距离消声壁约5.3 m,声纳接收阵面与水面基本垂直,如图5所示。目标实物为金属圆管,长度为2.05 m,直径约3.0 cm,带有一定弯度,周身用白布条包裹,两端有螺丝纹,如图6所示。 实验利用48×48阵元数目的平面阵对水池数据进行采集。接收阵形成128×128波束,在0~50 m探测范围内形成2 048个距离切片。对铁管目标数据进行处理,铁管的原始数据经过坐标转换得到的目标点云如图7所示。由图7可以看出,由于海洋环境的干扰,很难辨别出目标的轮廓。 图7 水池中铁管三维坐标系点云Fig.7 Point cloud in Cartesian coordinates of iron tube 对点云分别使用阈值去噪方法和LOF去噪方法,得到结果如图8所示。从图8(a)中可以看出,阈值去噪后已经能看出铁管的基本轮廓,但是仍会有一些离群点,容易对后续的构网结果造成偏差,模糊目标边界。而图8(b)中LOF去噪方法设定阈值去除大于1.2的点后,异常点数目相比图8(a)中减少为0,不存在模糊目标轮廓的干扰点,只保留了目标本身的点,使得目标轮廓能很好地体现。 图8 水池中铁管去噪后点云Fig.8 Point cloud after denoising of iron tube 对两种去除干扰点后的方法分别进行改进的三角网生长法建网,得到图9所示的结果。由图9可见,阈值去噪方法由于离群点的影响,网格中会出现不需要的三角形,使得铁管的边界被严重混淆。LOF方法相比而言有很好的效果。 图9 水池铁管构网结果Fig.9 Triangulation result of iron tube 本文通过实验数据分析,发现基于LOF算法的去噪方式相比于传统阈值去噪方式,能够在保持目标真实轮廓的前提下有效剔除异常噪点,得到更贴合实际的目标轮廓。另外,三维数据可视化的实时性要求低复杂度的算法实现,本文所提出的改进三角网方法大大简化了构网过程。然而LOF的阈值设定需要观察后手动设定,在将来可以考虑自适应地选取适合不同目标的阈值。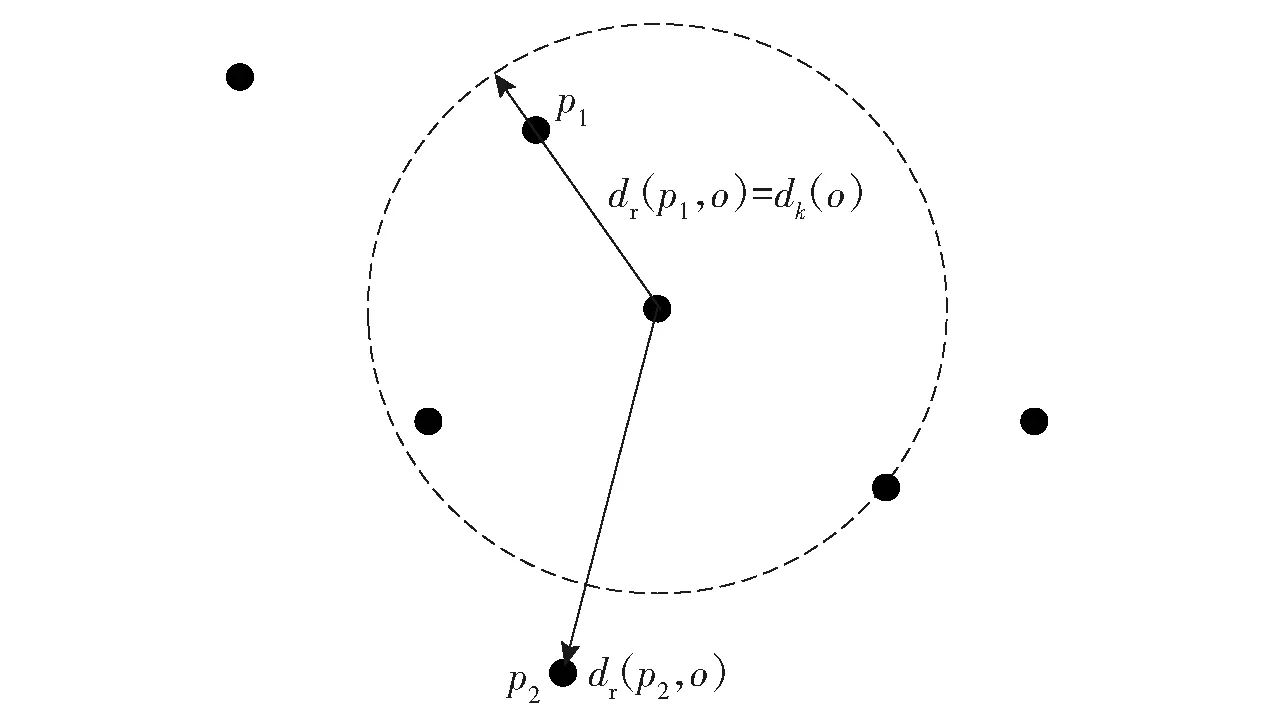
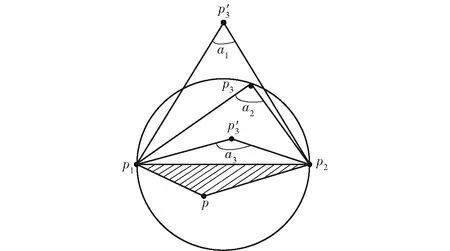
2.2 改进的三角网生长重建算法
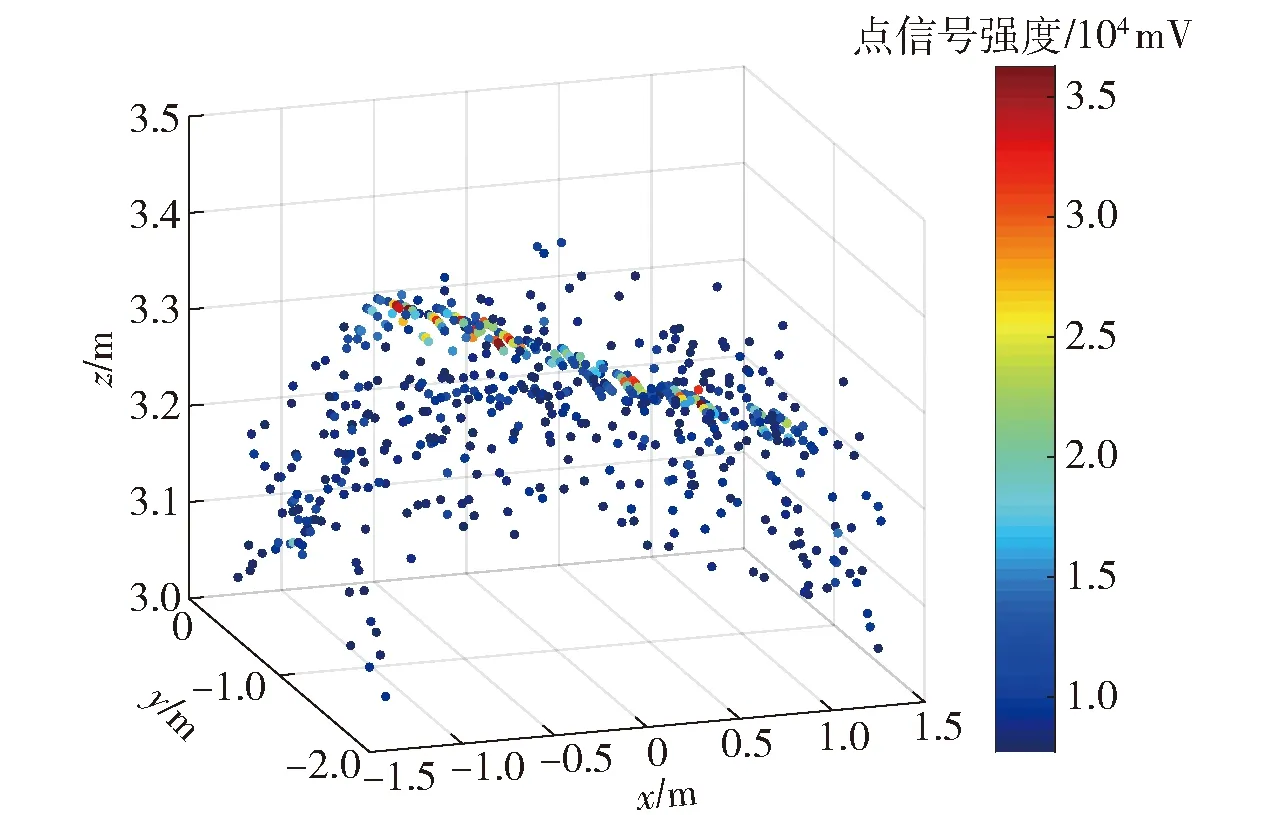
3 实验结果及分析
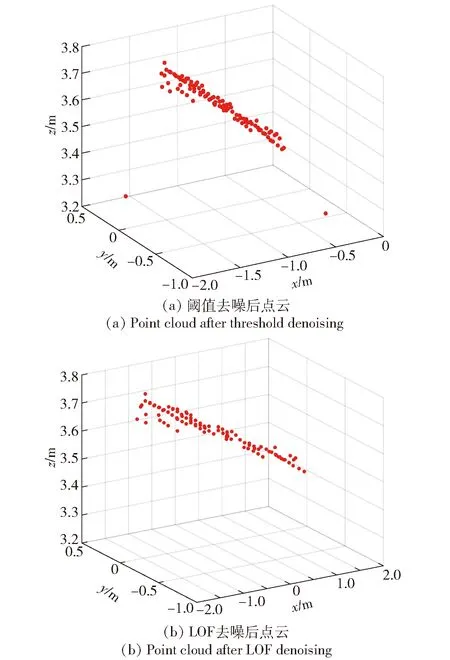
4 结论
