凸优化算法在有人/无人机协同系统航迹规划中的应用
2020-04-15陈清阳
李 樾,韩 维,陈清阳,张 勇
(1. 海军航空大学航空基础学院,烟台 264001;2. 国防科技大学空天科学学院,长沙 410073)
0 引 言
有人/无人机协同作战是指在信息化、网络化及体系对抗环境下,有人机与无人机联合实施攻击的作战方式[1]。该作战方式是潜在的第六代穿透型战机的发展方向之一[2]。美国于2015年提出“忠诚僚机”计划[3],并于2017年利用有人战斗机与由F-16改装的无人机验证了协同系统对地打击的效能,下一步计划由五代机控制无人机执行半自主/自主协同任务[4]。为充分发挥协同系统的优势,提高有人驾驶平台的安全性能和生存能力,研究协同系统的航迹规划技术是十分必要的。
目前,航迹规划从建模的方式上可分为两种,一种是基于加速度或过载等控制量来建立微分运动方程,将航迹规划作为最优控制问题进行研究;另一种是基于转弯角、航段长度而建立代数运动方程,相应的规划方法主要有图搜索、树搜索、势场法等[5]。本文以前者作为建模方式,其求解思路分为直接法和间接法。直接法将最优控制问题转化为有限维参数优化问题,用非线性规划方法进行求解,其缺点是求解精度不高;间接法则重点研究最优控制问题的一阶必要条件并将其转化为哈密顿边值问题,其缺点是收敛半径较小,对初值要求较高[6]。具体而言,求解最优控制问题的主要方法有伪谱法[7]、混合整数规划算法[8]以及启发式算法[9]等。其中,伪谱法在近年来较为流行,其具有良好的收敛性和较低的初值敏感度,常用的类型包括Gauss伪谱法、Legendre伪谱法和Radau伪谱法等;混合整数规划算法常采用CPLEX软件来求解,该软件是由ILOG公司开发的一种优化引擎,专门用来解决涉及线性规划、二次规划和二阶锥规划的典型问题,其求解速度快,具有基于超线性的加速功能[10];启发式算法包括遗传算法、模拟退火算法、神经网络、蚁群算法等,当用于多机航迹优化时,对初始解要求较高,且规划时间较长,不易收敛,给实际工程应用造成了不小难度。
近年来,凸优化理论得到不断完善,特别是在求解多维最优控制问题方面优势明显[11],其本质上属于直接法的一种,主要采用内点法进行求解[12]。凸优化理论在星际轨道转移、多智能体航迹规划以及无人机编队队形重构等领域均有应用。文献[13]对于小天体附着多约束轨迹优化问题,通过约束松弛、线性化、离散化过程,提出一种基于序列凸优化的航迹优化方法;文献[14]结合某航天器的姿轨控一体化推进系统配置,提出一种基于凸优化算法的制导方案;文献[15]以地面多机器人系统为研究对象,将一致性理论和序列凸规划思想结合,研究了系统的协同交汇问题;文献[16]以四旋翼为研究对象,将最优控制问题转化为若干二阶锥规划的子问题,并利用内点法求解机体避障航迹;文献[17]利用序列凸规划思想,将非凸最优控制问题近似为一系列凸优化子问题,解决了多无人机编队重构问题。
在目前基于凸优化理论的多机航迹规划研究中,缺乏对异构的固定翼集群的研究,特别是有人/无人机协同系统。对此,本文根据协同系统中有人机与无人机的任务特点,建立不同的航迹凸优化模型,同时从保证有人机飞行安全的角度出发,建立有人机与无人机航迹的时空关系,并采用序列凸规划的方法进行求解,以确保协同系统能够在复杂环境中安全、快速地抵达任务区域。
1 有人/无人机协同系统建模
1.1 协同系统的体系结构
有人/无人机协同系统本质上是异构的多智能体系统,有人机和各无人机均可视为其中的Agent[18]。多智能体系统的基本体系结构分为分布式、集中式以及混合式三类,针对有人/无人机系统,一般采用兼有集中式和分布式优点的混合式体系结构[19]。
设由M架有人机与N架无人机组成协同系统,其中多无人机之间构成分布式体系结构,有人机与无人机之间构成集中式体系结构。该混合式结构既可以充分发挥有人机中人的最高决策能力,又可以发挥多无人机应对突变信息的实时调整能力。
为简化系统,本文取M=1,N≥2进行研究。
1.2 协同系统运动模型的建立
设系统中飞机在空中无侧滑地飞行,且发动机推力与飞行速度方向重合,则可得到三维空间中飞机的点质量运动模型,具体如下
(1)
式中:下标i表示系统中的第i架飞机,i=1,2,…,M+N; (xi,yi,hi)表示飞机i在地面坐标系下的三维坐标; (γi,χi)表示飞机i的航迹倾角和航向角;Vi表示飞机i的地速;(nx,i,ny,i,nz,i)分别表示飞机i的水平轴向过载、水平法向过载和垂直法向过载;飞机i的控制量和状态量分别用集合ui和si表示,即ui=[nx,i,ny,i,nz,i]T及si=[xi,yi,hi,Vi,χi,γi]T。
1.3 协同系统控制模型的建立
在混合式体系结构中,有人机的ui和si作为其控制系统的输入,由航迹规划器离线求出,通过飞行员的操控生成相应地航迹,并作为输入进入编队规划器;编队规划器主要用于无人机编队的航迹规划,其充分考虑了有人机航迹的优先性,有利于保证有人机的绝对领导;通过编队规划器生成的ui和si,输入到各无人机制导系统中,并通过控制系统生成油门、舵面等控制量,最终利用飞机的运动模型输出实际飞行航迹;系统中导航系统的主要作用是计算飞机实际状态量与si的偏差,并生成修正指令。协同系统的航迹控制框图如图1所示。
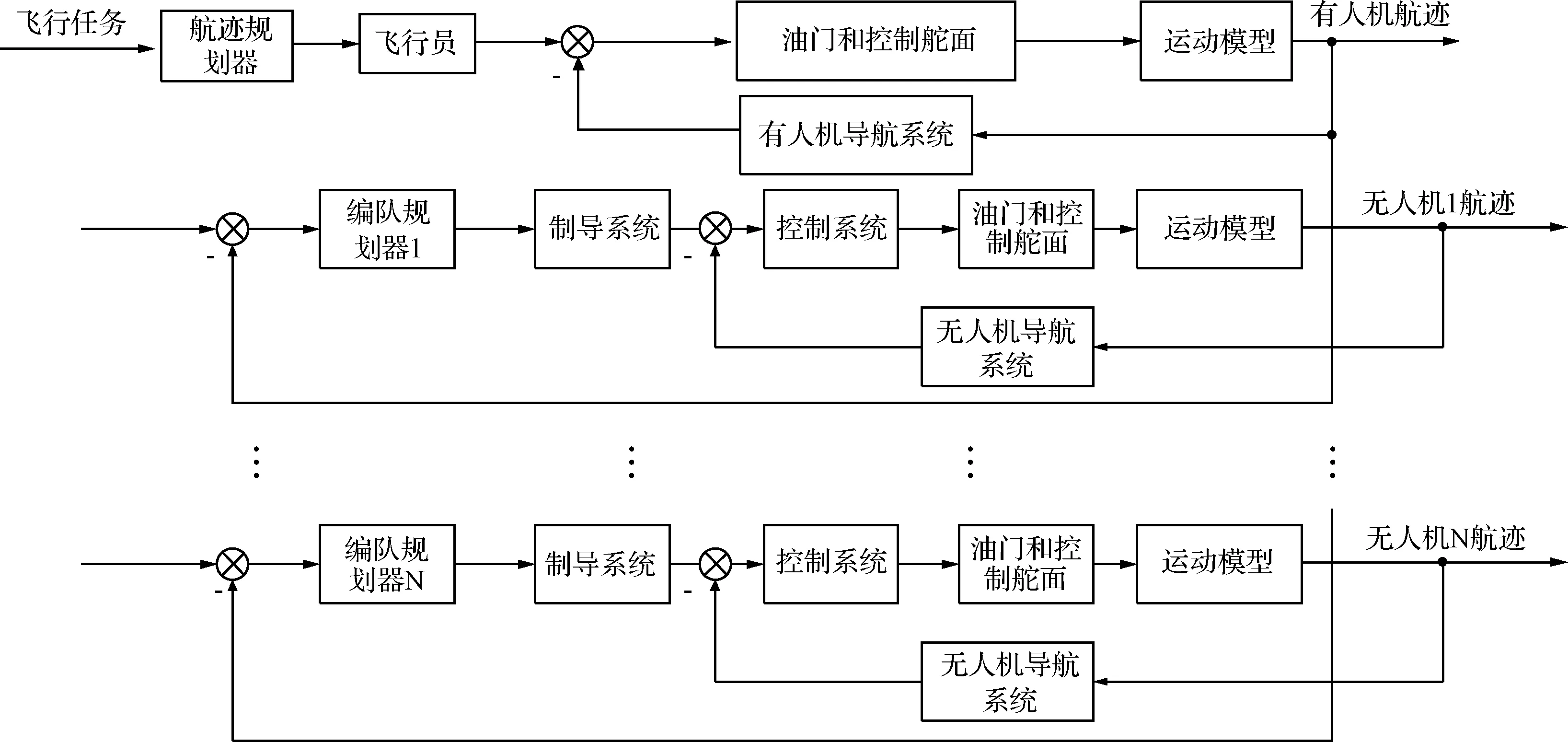
图1 协同系统航迹控制框图Fig.1 Block diagram of trajectory control in system
2 航迹规划器的设计
2.1 约束条件与目标函数
在飞行过程中,有人机应始终满足状态量和控制量的幅值约束,并且控制量的变化率应在一定的范围内,即
(2)
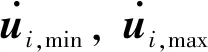
(3)
另外,防碰撞约束是航迹规划器应重点考虑的约束之一,由于文中取M=1,因此只需考虑与外部威胁的碰撞。假设在规划空间中总共探测到M0个静态威胁,用圆柱体近似表示,并假设其高度远大于飞机的高度幅值,则防碰撞约束可表示为下式
(4)
式中:矩阵E=[I2×2,O4×4],pobs,m和rm分别是外部障碍的横截面圆心坐标和半径。
在此基础上,确定航迹规划器的目标函数。在协同系统中,有人机具有绝对领导权,其续航能力直接影响整个系统的作战周期。因而,从增加协同系统作战周期的角度出发,选取最小化耗能量为目标函数,得到优化模型为
(5)
2.2 模型凸化
利用凸优化理论进行求解时,要求目标函数和不等式约束均为凸函数,等式约束为仿射函数,而式(5)中含有非线性运动方程和非凸的约束条件,因而需要进行近似和凸化。
梯形法是一种求解常微分方程初值问题的常用方法,针对非线性运动方程,利用梯形法可得到离散化状态量等式约束,如式(6)
si[k+1]=si[k]+Δt/2·[f(si[k],ui[k])]+
f(si[k+1],ui[k+1]),
k=0,1,…,K-1, Δt=(tf-t0)/K
(6)
式中:si[k],ui[k]分别为离散时刻tk的状态量和控制量,K为已知的离散点数,且相邻离散点之间用零阶保持器控制,所求Δt是离散的时间步长。
借鉴基准轨迹的思想[11]对式(6)进行线性化,具体表达式如下
Ak+1·si[k+1]+Ak·si[k]+Bk+1·ui[k+1]+
Bk·ui[k]+(Ck+Ck+1)·Δt+Dk+Dk+1=0,
k=0,1,…,K-1
(7)
式中:
(8)
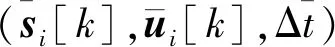
另一方面,式(4)中非凸约束条件的离散化及凸化过程详见文献[17]。具体地,通过联立式(7)和式(9),可将有人机的状态量用控制量的仿射函数表征,从而达到约束凸化的目的。
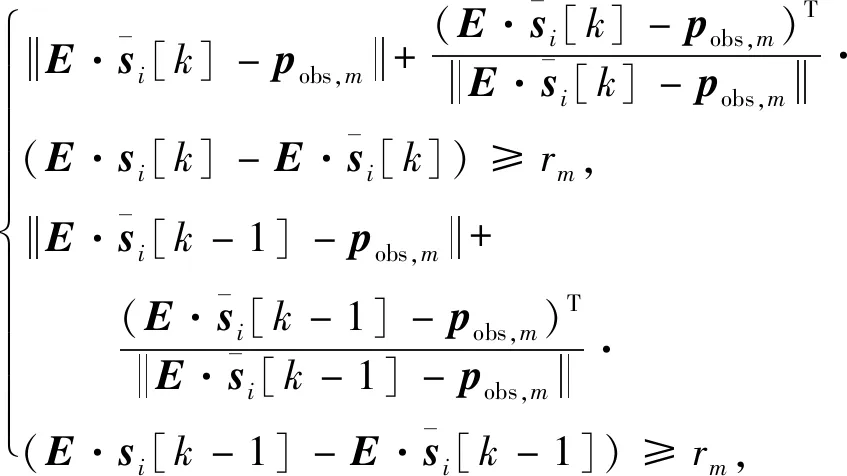
i=1,2,…,M,m=1,2,…,M0,k=1,…,K
(9)
至此,得到了航迹规划器的凸优化模型,如式(10)
(10)
式中:式(2)中t取各离散时刻,下文中状态量的幅值约束均采用该方式进行处理。求解后输入到编队规划器中。
3 编队规划器的设计
3.1 与航迹规划器的异同
与航迹规划器类似,在对编队规划器设计时也需要考虑飞机状态量和控制量的幅值约束以及外部防碰撞约束,具体同式(2)和式(4)。
与航迹规划器的不同,表现在以下几方面:
1)协同系统中的无人机与有人机的任务不同,其主要负责侦查、打击和掩护等任务,因此其机动性要强于有人机,即状态量和控制量的幅值要大于有人机。
2)编队规划器所考虑的约束更多。具体包含无人机编队内部约束以及协同时空约束。
(1)基于前者,由于N≥2,因此需考虑无人机之间的碰撞,即应约束任意时刻的两架无人机的机间距离均大于设定的安全距离,具体如
(11)
式中:F=[I3×3,O3×3],Rt是机间三维安全距离,ts和te分别表示无人机航迹规划的初始时刻和终端时刻。
同时,为更好地发挥多无人机在系统中的优势,系统中多无人机在ts和te时刻需保持一定的编队构型,具体的编队构型约束如下
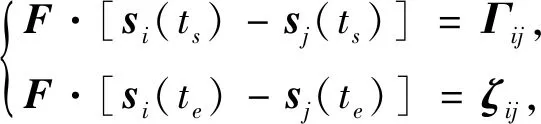
(12)
式中:Γij和ζij分别为ts和te时刻的机间相对状态矩阵,通常从提前设定的编队队形库中提取。
(2)针对协同时空约束,编队规划器应考虑时序约束、终端状态量关系约束及与有人机的防碰撞约束。
设系统中多无人机与有人机在同一时刻开始变换航迹,通常多无人机要先于有人机抵达任务区域进行侦查等任务,一旦发现敌情可令有人机改变航迹,确保飞行员安全。因而无人机航迹的终端时刻和状态量si(te)是非固定的,具体满足式(13)~(14)的约束条件
(13)
(14)
式中:第一式:G=[I3×3,O3×3],R0为一个三维空间,表示无人机i相对于有人机j所处的区域,由于多无人机满足构型约束(12),因此,第一个式中i只需取1~N中的任意一值即可;第二个式中:H=[O4×4,I2×2],表明各无人机在航迹终端的航迹角均与有人机保持一致。
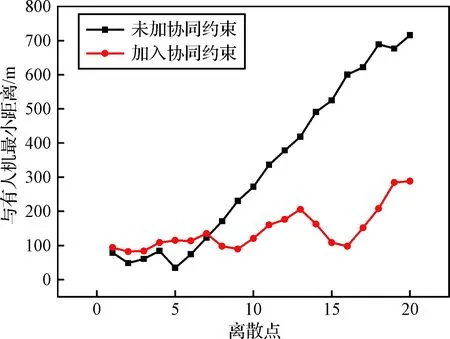
与有人机的防碰撞约束与式(11)类似,其关键是要确定同一时刻下的三维坐标,并进而确定机间距,其约束如
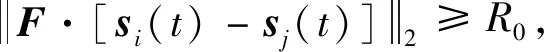
(15)
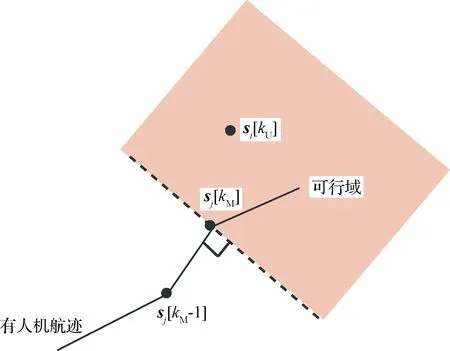
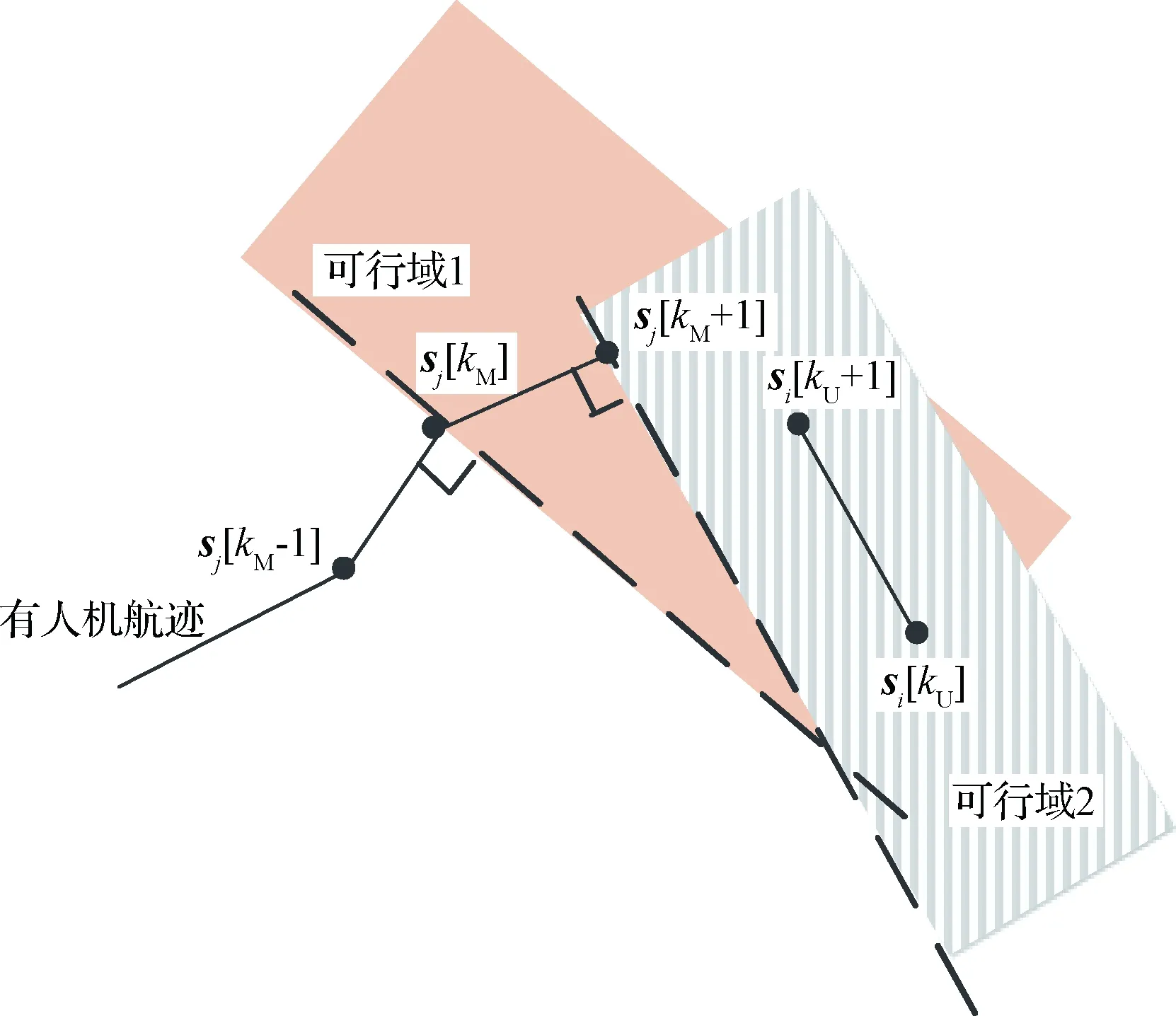
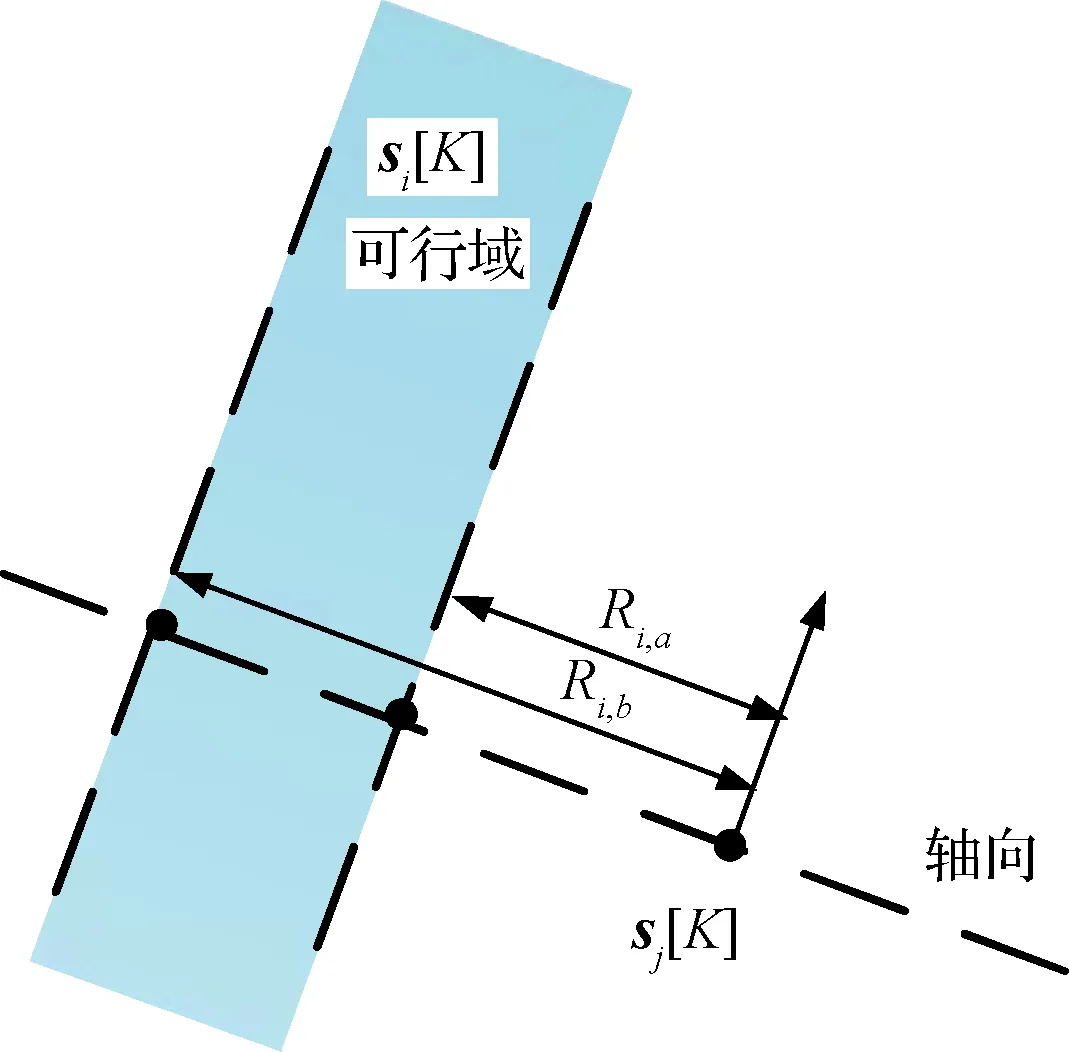
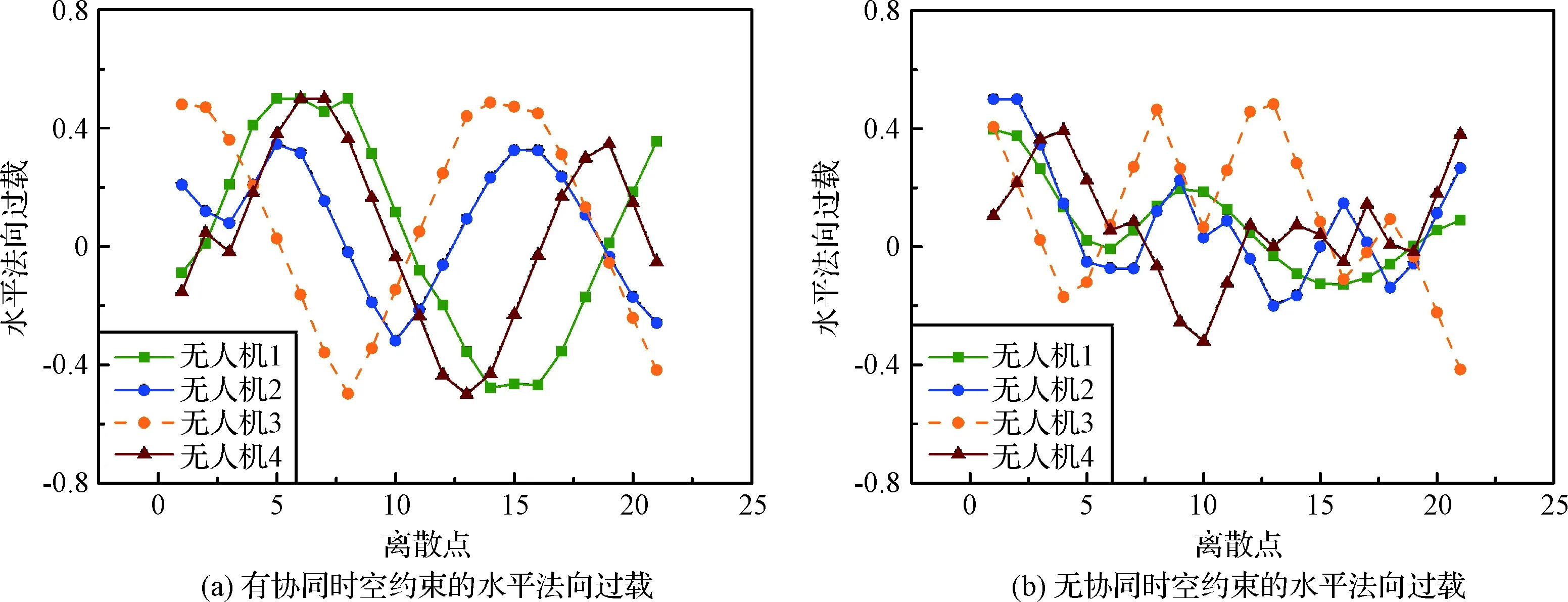
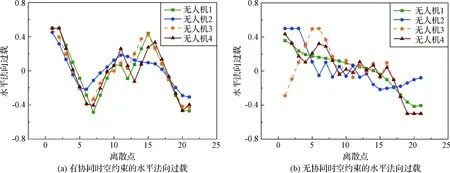
式中:R0是有人机与无人机间的安全距离;时间t的上限为te,即默认多无人机到达目标区域后保持新队形继续飞行,在te 3)编队规划器的优化目标函数与航迹规划器不同。由于无人机相比有人机具有重量轻、成本低、适应性强等特点,因而对其到达任务区域的时间要求高于对其续航的要求,则目标函数选取为最短到达任务区的时间。 至此,得到编队规划器的优化模型 (16) 与航迹规划器的凸化过程类似,首先设定K个离散点,离散时间步长未知,用Δt0表示,则任意离散时刻可表示为 tk=ts+k·Δt0, 0≤k≤K,ts≤tk≤te (17) 编队规划器和航迹规划器所共有的约束(2)、(7)、(9),在此节不加赘述。另外,无人机内部防碰撞约束(11)的凸化过程在文献[16]中已详尽推导,约束如 (18) 式中:第二式所含η为机间安全距离的修正系数,R是二维平面内安全距离,通过该式的约束,可进一步保证离散时间段内无人机在三维空间内的飞行安全。 本节重点分析协同时空约束的凸化过程。由于无人机与有人机非同时到达目标区域,因而在凸化无人机与有人机的防碰撞约束前,应首先确定二者所对应的离散时刻对(kU,kM)所组成的集合。结合时序约束(13),得到的表达式,如 1≤kU≤K, 1≤kM≤kU} (19) (20) 该式在几何上的示意图如图2所示,si[kU]的可行域为图中阴影区域,其边界垂直于有人机航迹上两相邻离散点sj[kM-1]与sj[kM]的连线,并且位于有人机前进方向的一侧,这有利于保证无人机先于有人机抵达任务区域的时序约束。另外,由于sj[kU]位于sj[kM-1]至sj[kM]之间,通过式(20)约束,可保证si[kU]至si[kM]与sj[kU]至sj[kM]无碰撞。 图2 与有人机防碰撞约束的凸化示意图Fig.2 Convexification of avoiding MAV constraint 除了保证离散时刻点的飞行安全,有人机与无人机在相邻离散时间对内所对应的时间区域也存在碰撞可能,因此在式(20)的基础上还应进一步约束,具体如 E·sj[kM+1])≥0, i=1,2,…,N,j=1,2,…,M,kM≥1, (kU,kM)∈ (21) 其原理与式(20)类似,即建立了si[kU]与sj[kM],sj[kM+1]段航迹的关系,联立式(20)和式(21)可得到图3的示意图,si[kU]的可行域为图中可行域1与可行域2的交集,由于si[kU+1]一定位于可行域2内,因此由凸集性质可知无人机在离散点si[kU]至si[kU+1]段内不会与有人机sj[kM]至sj[kM+1]航迹发生碰撞,从而易推出si[kM]至si[kU+1]段内不会与sj[kM]至sj[kU+1]航迹发生碰撞,结合已分析的kU至kM时刻的航迹关系,可知有人机与无人机始终不会发生碰撞。 图3 离散点间防碰撞约束凸化示意图Fig.3 Convexification of inter-sample threat avoidance constraint 另一方面,由于无人机与有人机的终端航迹角相同,因此对于终端状态量约束只需对位置关系约束进行相应地近似与凸化,以图4中si[K]相对于sj[K]的轴向约束为例,可得到 ∀i∈{1,2,…,N},j=1,2…M (22) 式中:Ri,a,Ri,b分别为有人机与编队中无人机i所允许的最小、最大轴向距离。 纵向约束凸化过程与轴向类似,在此不加赘述,且由多个半平面相交组成的可行域仍为凸集。值得一提的是,协同时空约束的凸化与前文提到的防碰撞等约束的凸化类似,也分别是原约束条件成立的充分条件而非充要条件,会带来一定的保守性,目前的研究中多采用序列凸规划的方法来进行缓解[20]。 至此,可以得到编队规划器的凸优化目标函数,与航迹规划器不同,该目标函数约束众多,且进行了一定程度的近似,因而易出现无解的情况,文献[21]所用的罚函数方法,得到如下目标函数: (23) 式中:优化变量Z包括集合zi及离散时间步长Δt0,集合zi包含各无人机的状态量及控制量,即 Z=[z1,z2,…,zN, Δt0]T,zi=(si[0],si[1],…,si[K],ui[0],ui[1],…,ui[K]),i=1,2,…,N (24) 等式约束Aeq·Z=beq包含式(7),不等式约束Ain·Z≤bin包含式(2)、(9)、(13)、(18)~(22);μeq和μin分别为等式约束和不等式约束的比例系数。 图4 终端位置轴向约束凸化示意图Fig.4 Convexification of axial constraint in terminal position 之前的文献中,已校验过凸优化算法在单机和同构的多机航迹规划中高效且准确的求解能力,因此本节针对典型队形之间的切换问题,重点校验协同时空约束的效果。 设协同系统由五架(M=1,N=4)飞机组成,初始构型为菱形护航队形。该构型中,有人机位于编队中心位置,四架无人机位于其四周组成菱形,且处在同一高度。该构型的最大优势是能够保证有人机的飞行安全,当协同系统面对空中来袭时,有人机能在无人机的掩护下进行撤离,特殊情况下,无人机还可以通过“自杀”的方式为有人机争取更多的逃离时间和空间。该构型的分布如图5所示,初始状态量如表1所示。 终端构型设为五边攻击队形。该构型中,有人机位于无人机后方,且高于四架无人机所在平面,五架飞机的投影组成一个五边形,具体分布如图6所示。该队形主要用于执行攻击任务,面对敌机时,在最前方无人机的牵制下,后排无人机迅速从两侧加速包抄,形成对敌机的包围,有人机在后方相对安全,并能俯瞰全局,利于进行全局指挥。设定tf时刻,有人机状态量s(tf)=[250,1200,150,20,π/2,0]T,无人机的相对位置矩阵ζij如表2所示,表中列出的是i=1的情况,同i值下,取Ri,a=180,Ri,b=220。 图5 菱形队形分布示意图Fig.5 Distribution diagram of rhombic formation 表1 菱形队形中各机状态量表Table 1 State information of rhombus formation 另外,规划空间内随机生成三个柱形障碍,截面圆心及半径分别为 (25) 图6 五边攻击队形分布示意图Fig.6 Distribution diagram of pentagon attack formation 表2 无人机相对状态矩阵Table 2 UAV relative state matrix 有人机的参数设定如 (26) 无人机的参数设定如 i=1,2,3,4 (27) 其他参数设定如 (28) 然后利用凸优化工具包CVX中的MOSEK求解器对系统航迹进行规划,该求解器与SEDUMI、GUROBI及SDTP3等求解器相比,更适合求解优化变量较多的问题,且效率更高。同时,为减少初始预测的基准航迹对模型求解带来的误差影响,也为降低约束带来的保守性,本文采取序列凸规划[17]的思想进行迭代求解,其参数设定与文献[17]保持一致。 为校验协同时空约束的效果,首先对式(10)进行求解,并将得出的有人机航迹输入到编队规划器中;其次对完整的编队规划器模型(23)进行求解,得到Zc;之后,将Zc中的si[K]作为固定的已知量输入到模型(23),并求解未加约束(19)~(22)的模型(23),得到Zs。仿真对比结果如表3及图7~图11所示。其仿真平台为Matlab2013a,计算机配置为Intel酷睿i7处理器,主频3.60 GHz,内存32 G,64位win7操作系统。 表3 有无协同时空约束的优化结果对比Table 3 Results of with or without synergetic spatial-temporal constraints 图7 协同时空约束效果对比图Fig.7 Comparison between with or without synergetic spatial-temporal constraints 图8 多无人机内部最小间距对比图Fig.8 History of minimum distance of UAVs 图9 无人机与有人机最小间距对比图Fig.9 History of minimum distance between UAVs and MAV 图10 水平法向过载对比图Fig.10 History of horizontal normal overload 图11 水平轴向过载对比图Fig.11 History of horizontal axial overload 结果中没有单独列出有人机的优化结果,在K=20的情况下,其优化目标函数值仅为22.54,说明其只在必要时刻实施机动,能达到减少耗能的目的,具体航迹详如图7所示,从该图中还可以看出协同系统在有/无协同时空约束时,均可实现从初始菱形护航队形到五边形攻击队形的变换,且与外部障碍无碰撞,不同的是,由表3可知,无协同约束时所求Δt0小于有协同约束时的Δt0,两者在终端时刻的离散时间对分别为(20,11)及(20,17),有人机在无人机形成新队形后的航迹在图7中用带五角星的虚线进行区分;从图8中可看出,在有/无协同时空约束下,同时刻的无人机机间距离均大于安全距离,即不会发生碰撞;由图9可知,在不同离散时刻,添加协同时空约束后的无人机与有人机的最小间距始终在80 m以上,而未添加该约束时,在前7个离散时刻,机间距均小于80 m,甚至出现过只有34.2 m的情况,在第7个离散点之后,无人机迅速接近目标区域,离散时间对的差不断增大,导致最小机间距不断增大;从图10~11可看出,各无人机过载均在幅值范围内,但由图11可看出,添加协同时空约束的情况下,四架无人机初始的水平轴向过载均在最大值附近,其原因是无人机通过迅速加速的方式以减少约束(20)~(21)带来的罚函数项,特别是无人机1和无人机4,其位置坐标沿初始航向落后于有人机,因而其最大水平轴向过载维持的时间更长,但在最大过载的约束下,仍无法完全消除该罚函数项,同时各机的水平法向过载也因幅值的约束而存在类似的情况,这也解释了表3中有协同时空约束时目标函数值偏大的原因。 综上,添加时序约束和与有人机防碰撞约束可进一步保证协同系统的飞行安全,但会相应地牺牲无人机到达任务区域的时间;通过将终端位置约束由固定点改为约束区域,能为系统的航迹规划提供更多地可能,且求解耗时相近,未降低求解效率。因而,协同时空约束的添加对系统航迹规划是十分必要的。 本文根据凸优化理论,对有人/无人机协同系统的航迹规划进行了研究。得到如下结论: 1) 给出了协同系统航迹控制的框架,并根据有人机与无人机任务特点的不同,分别设计航迹规划器和编队规划器;选取最小耗能量和最短时间到达任务区域为各自的目标函数。 2) 相比航迹规划器,编队规划器的约束更为复杂;添加协同时空约束,能有效保证系统的飞行安全,为系统的航迹规划和队形变换提供更多地可能。 3) 近似和凸化后的优化模型,可采用凸优化算法进行求解,并通过具体的数值仿真验证了其有效性。 当协同系统的组成更为复杂,特别是有人机与无人机数量明显增加时,考虑集群互补,集群毁伤之后的重组与重构并构建更为复杂的外部环境模型是下一步值得研究的内容。3.2 协同时空约束的凸化
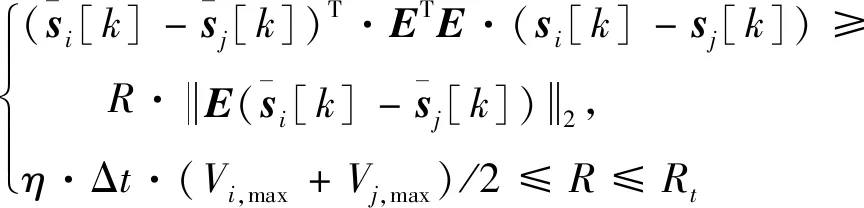
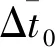
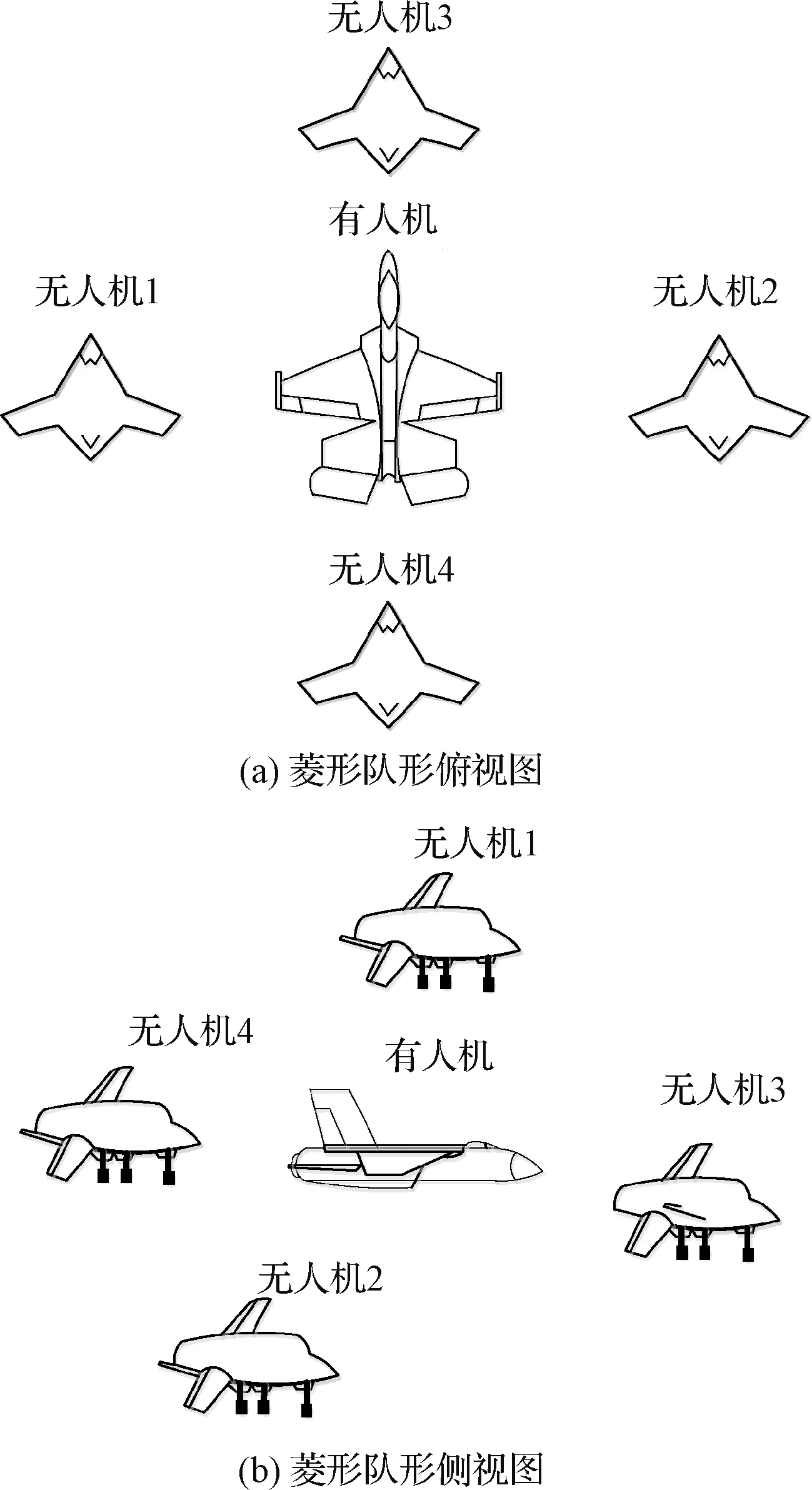
4 仿真校验

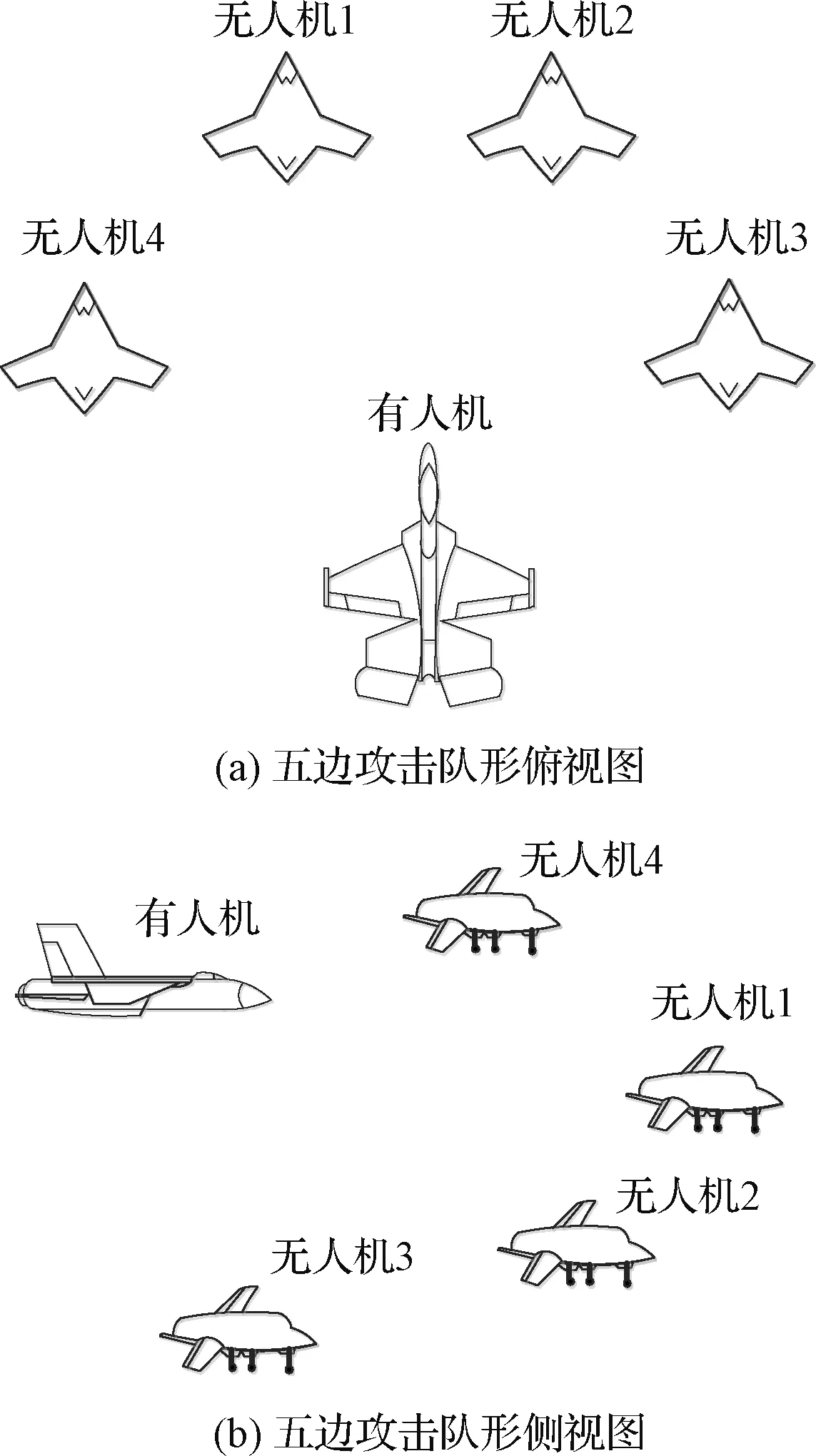

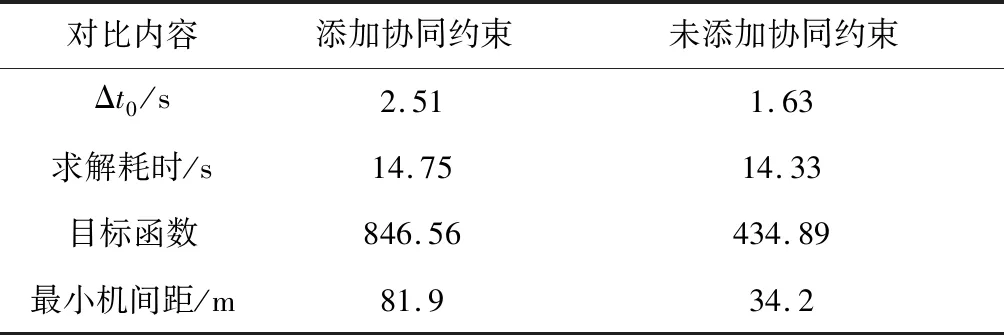
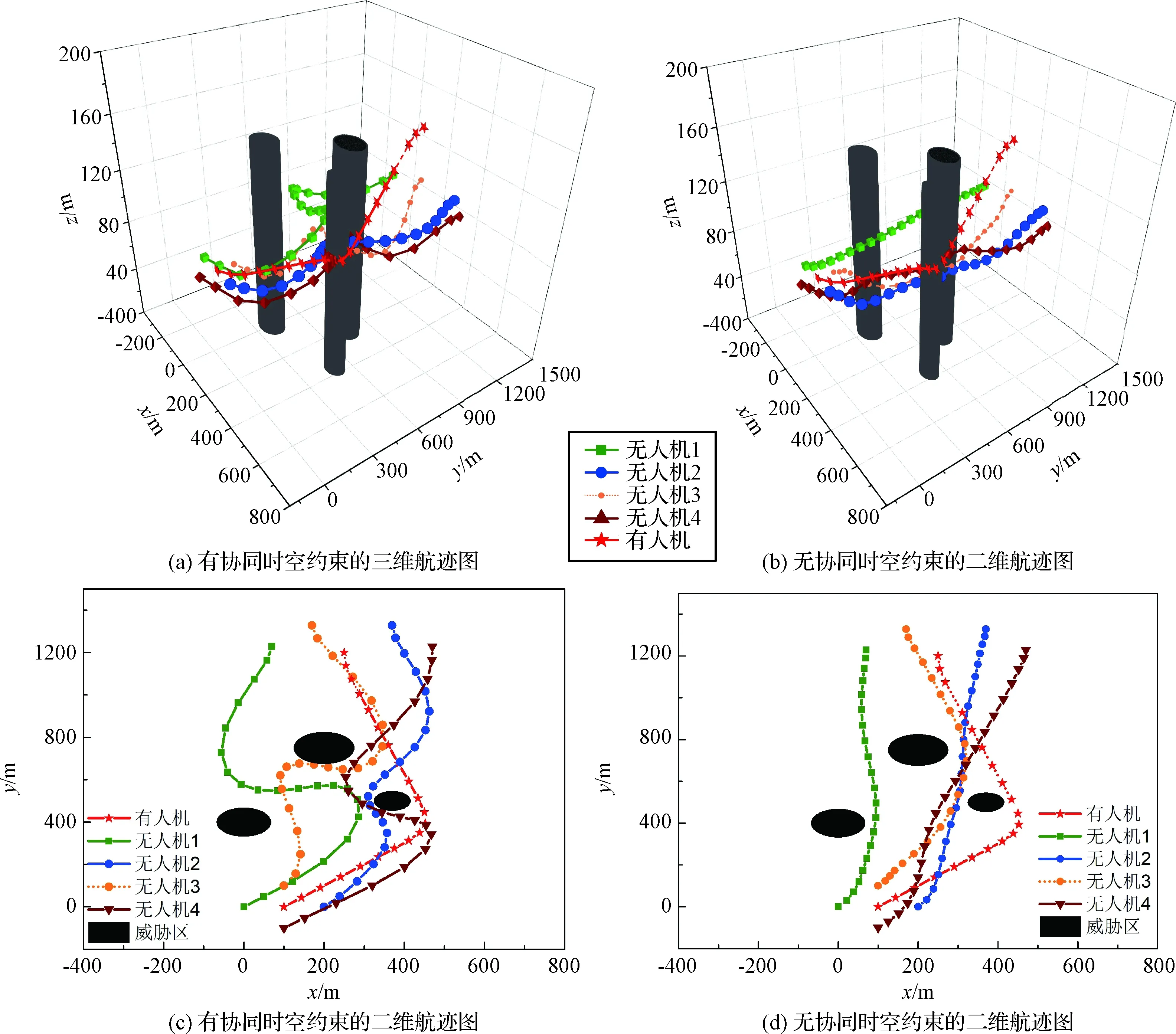
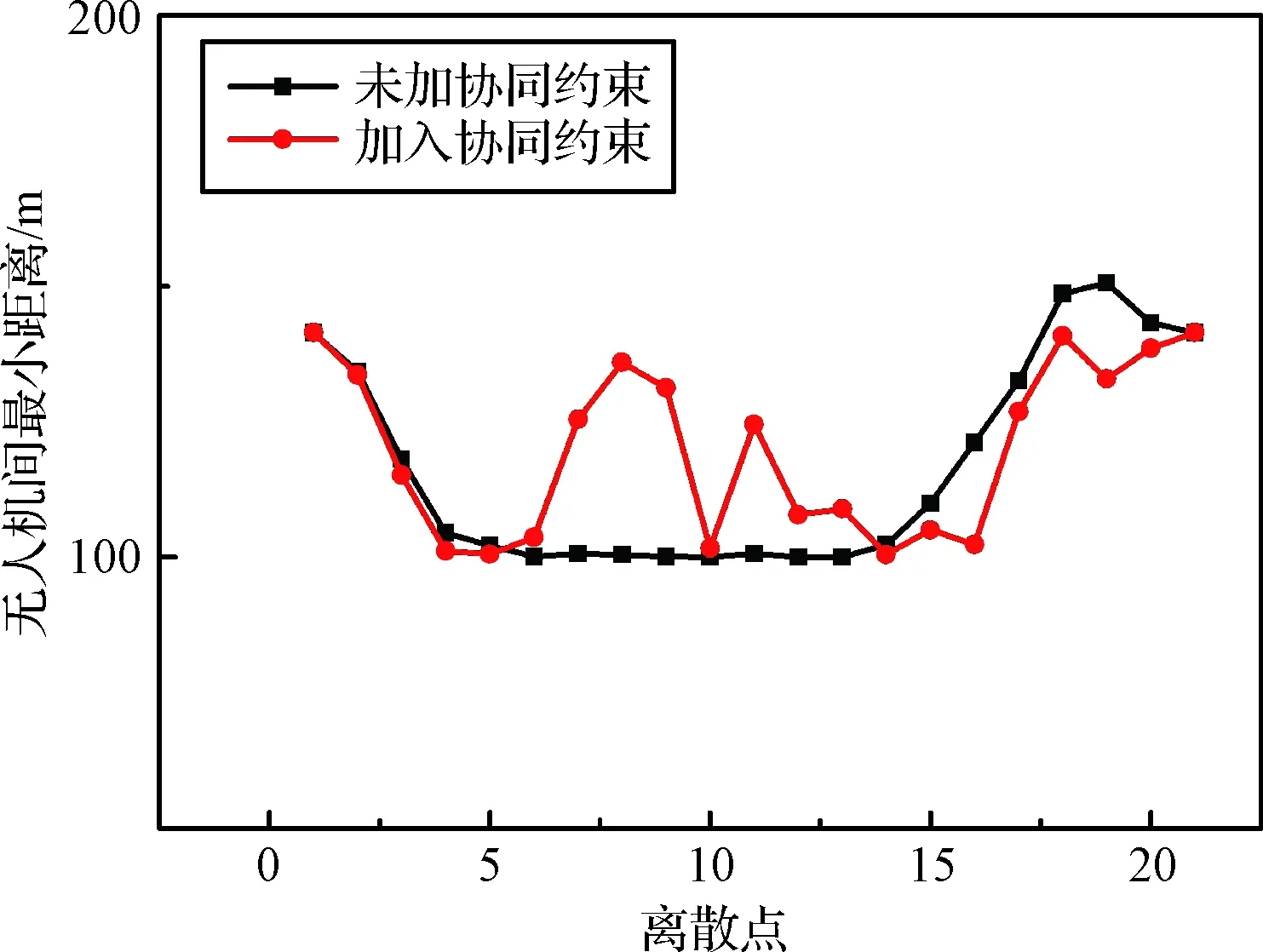
5 结 论
